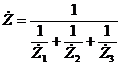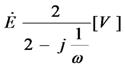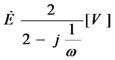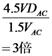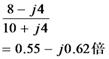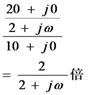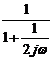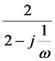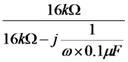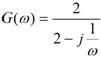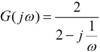|
側偀傫偪傖偭偰揹巕岺妛
乣丂偁傞偄偼帺揮幵偲岎棳丂乣
妝偟偄揹巕岺嶌偺偨傔偺乮偄偄壛尭偝傪嬌傔偨乯揹婥偺抦幆
|
2017擭10寧25擔
側偀傫偪傖傫偰揹巕岺妛882.doc丂
By dokunewon
侾. 杮彂偺栚揑偲摿挜
杮彂偼庯枴偱揹巕夞楬傪妝偟傓曽偺偨傔偵嶌惉偟傑偟偨丅偮傑傝丄夞楬傪棟夝偟偨傝愝寁偟偰梀傇曽傪懳徾偵偟偰偄傑偡丅偙偺偨傔丄杮彂偼師偺曽恓偱嶌惉偟偰偄傑偡丅
侾丏悢妛傪朰傟偨恖偱傕乮娙扨側嶼悢偑偱偒傟偽乯揹巕夞楬偑妝偟傔傞傛偆偵偡傞
惓妋偝偼寜偔媇惖偵偟偰丄乽幃乿偱偼柍偔乽恾乿傪巊偭偰丄擔忢惗妶偵歡偊偰愢柧偟偰偄傑偡丅寁嶼偼俤倶們倕倢偱峴偄傑偡丅
俀丏夞楬恾偐傜夞楬偺摦嶌傪姶偠傜傟傞傛偆偵偡傞
摍壙夞楬偵抲偒姺偊偢偵丄夞楬恾忋偱摦嶌傪愢柧偡傞偙偲偱丄夞楬恾偐傜捈愙偵摦嶌傪撉傒庢傝丄夞楬偺摦嶌傪姶偠側偑傜夞楬恾傪昤偄偰妝偟傔傞傛偆偵岺晇偟偰偄傑偡丅
俁丏棟夝偑怺傑傞傛偆峔惉偡傞
夝愢偲楙廗栤戣傪岎屳偵慻傒崌傢偣丄幙栤偵摎偊側偑傜撉傒恑傔傞偙偲偱丄棟夝偑怺傑傞傛偆偵峔惉偟偰偄傑偡丅
係丏梊旛抦幆偑柍偔偰傕撉傔傞傛偆偵偡傞
婎慴揑側撪梕傕昁梫偵墳偠偰徯夘偟丄梊旛抦幆偑柍偔偰傕棟夝偱偒傞傛偆偵峔惉偟偰偄傑偡丅
杮彂偼丄暘傝堈偝傪廳梫帇偟偡偓偨寢壥乽晄惓妋乿側偆偊丄乮屄恖偑嶌惉偟偰偍傝丄峑惓偑峴偒撏偐側偄偨傔乯乽岆帤丒扙帤丒岆嶼摍乿偑懡偄偙偲傪偛椆彸偔偩偝偄丅
僾儘偺僄儞僕僯傾偐傜乽偙傫側愢柧偱偼埨慡偵摦嶌偡傞婡婍偼愝寁偱偒側偄乿偲旕擄偑偁傞偺偼摉慠偱偟傚偆丅偟偐偟丄巚偄弌偟偰偔偩偝偄丅偁側偨偑巕嫙偺崰丄怓乆側夞楬傪嶌偭偰偼夡偟偨桖夣側巚偄弌傪丅偦偺傛偆側妝偟偝傪枴傢偆壓抧傪採嫙偡傞偺偑杮彂偺栚揑偱偡丅傑偢偼乽埨慡偠傖側偄偗偳丄堦墳偼摦嶌偡傞傛偆偵愝寁偱偒傞乿強傑偱峴偒傑偟傚偆丅
|
杮彂偺晹暘傗慡懱偼丄挊幰偺彸戻側偟偵丄擟堄偵暋幨傗夵椙傪峴偄丄梡搑傗桳彏丒柍彏傪栤傢偢攝晍偡傞偙偲偑偱偒傑偡丅岆傝偺掶惓傗傛傝暘偐傝堈偔偡傞偨傔偺夵椙偼娊寎偝傟傑偡丅扐偟丄暋幨傗夵椙傪峴偄丄攝晍偡傞挊嶌暔偵偼丄杮榞撪偺儊僢僙乕僕傪偦偺傑傑揮嵹偟丄挊嶌暔偺晹暘傗慡懱傪丄挊幰偺彸戻側偟偵丄擟堄偵暋幨傗夵椙傪峴偄丄桳彏丒柍彏傪栤傢偢攝晍偡傞偙偲傪嫋壜偟側偔偰偼側傝傑偣傫丅
by dokunewon
|
杮彂偺偁傜備傞娭學幰偼丄杮彂偺忣曬偲偦偺塣梡寢壥媦傃丄偦偺塭嬁偵偮偄偰丄偐偐傞懝奞偺敪惗壜擻惈傪椆抦偟偰偄傞応崌偱偁偭偰傕丄捈愙揑丄娫愙揑丄嬼敪揑丄寢壥揑懝奞丄堩幐棙塿丄挦敱揑懝奞丄傑偨偼摿暿懝奞傪娷傓慡偰偺懝奞偵懳偟偰丄忬嫷偺偄偐傫傪栤傢偢堦愗愑擟傪晧偄傑偣傫丅
杮彂偼慡偔怴偨偵彂偒婲偙偟偨傕偺偱偡丅偮傑傝丄巹帺恎偺夁嫀偺挊嶌暔傪僐僺乕丒儁乕僗僩偡傞偙偲偼傕偪傠傫丄嶲徠偡傞偙偲傕偣偢偵丄敀巻偺偺忬懺偐傜嶌惉偟偨傕偺偱偡丅偙傟偵傕偐偐傢傜偢丄帺慠壢妛尰徾傪暯堈偵愢柧偡傞偲偄偆惈幙忋丄巹偑夁嫀偵嶌惉偟偨彂柺偲椶帡偺昞尰偑尰傟傞壜擻惈偑偁傝傑偡丅
傑偨昅幰偑庒偄崰偵丄柤挊亀僾儘僌儔儉妛廗偵傛傞敿摫懱夞楬嘥嘦亁乮怑嬈擻椡奐敪嫵嵽埾堳夛乯偱曌嫮偟偨偨傔丄堦晹摨彂偲帡偨昞尰傗楙廗栤戣偑昞傟傞孹岦傕偁傝傑偡丅傕偪傠傫嶲徠偟偰堷偒幨偟偨晹暘偼堦愗偁傝傑偣傫偑丄庒偄帪婜偵崗傒崬傑傟偨婰壇偼堦惗巆偭偰偟傑偆寢壥偲偟偰丄乮摨彂偑柤挊偱偁傞徹偱偁傞偲峫偊偰乯偛姩曎偔偩偝偄丅
侾. 捈棳夞楬
悈摴偐傜棳傟弌偡悈偺傛偆偵丄偄偮傕摨偠岦偒偲戝偒偝偱揹棳偑棳傟偰偄傞夞楬傪乽捈棳夞楬乿偲屇傃傑偡丅
俀. 僆乕儉偺朄懃
棯偟偰僆乕儉懃偲傕屇傃傑偡丅夞楬傪峫偊傞偲偒丄僆乕儉懃偼壗搙偲柍偔巊偄傑偡丅偙偺偨傔丄弖娫揑偵巊偊傞傛偆偵偟偰偍偔偲丄僗儔僗儔偲夞楬偑撉傔傑偡丅
|
僆乕儉懃偼丄師偺傛偆偵峫偊傞偙偲偱丄宱尡偑愺偔偰傕慺憗偔巊偊傑偡丅
丒揹埑偑弌偰偒偨傜丄昁偢妱傜傟傞
丂丒揹埑偑弌偰偙側偗傟偽丄憃曽傪妡偗傞
|
揹埑偼妱傜傟傞両
|
偺俀偮偱偡丅椺偊偽丄師昞偺傛偆偵巊偄傑偡丅
|
忬嫷
|
峫偊曽
|
寁嶼
|
|
侾俀倁偱係俙棳傟偨
|
揹埑偺侾俀偼妱傜傟傞
|
侾俀亐係亖俁兌
|
|
俁兌偵侾俀倁偑妡偐偭偨
|
揹埑偺侾俀偼妱傜傟傞
|
侾俀亐俁亖係俙
|
|
俁兌偵係俙棳傟偨
|
揹埑偑弌偰偙側偄乮妡偗傞乯
|
俁亊係亖侾俀倁
|
俁. 俤倶們倕倢偲倣俙傗倠兌乮扨埵愙摢岅乯
俤倶們倕倢偵乽巜悢乿偱擖椡偡傞偙偲偱丄扨埵愙摢岅乮杮崁偲師崁偱偺傒丄扨偵乽扨埵乿偲彂偒傑偡乯傪庤憗偔張棟偱偒傑偡丅偨偲偊偽丄俆兪俙側傜丄5E-6丄偲丄俀俀侽倠倁側傜丄220E3偲偄偆傛偆偵丄抣偺屻偵乮乽扨埵乿偵懳墳偟偨乯乽巜悢乿乮E3摍乯傪晅偗偰擖椡偟傑偡丅椺偊偽乽E3乿偼乽1000乿乮僛儘俁偮乯乽E-3乿側傜乽0.001乿乮侾偺慜偵僛儘俁偮乯傪堄枴偟傑偡丅壓昞偵丄扨埵偵懳墳偡傞巜悢傪帵偟傑偡丅
扨埵傪巜悢偱擖椡偡傞
|
扨埵
|
f
僼僃儉僩
|
p
僺僐
|
n
僫僲
|
兪
儅僀僋儘
|
m
儈儕
|
k
僉儘
|
M
儊僈
|
G
僊僈
|
T
僥儔
|
|
巜悢
|
E-15
|
E-12
|
E-9
|
E-6
|
E-3
|
E3
|
E6
|
E9
|
E12
|
扨埵傪巜悢偱擖椡偟偨応崌丄俤倶們倕倢偵偼棁偺抣乮侾侽倠側傜丄侾侽侽侽侽乯偑擖椡偝傟偰偄傑偡丅
巜悢傪擖椡偟偨僙儖傗丄巜悢傪尦偵寁嶼偟偨僙儖偺昞帵宍幃偼丄帺摦揑偵乽巜悢乿偵曄峏偝傟傑偡丅巜悢偱偼側偔丄僛儘傪暲傋偰昞帵偟偨偄偲偒偼丄昞帵宍幃傪乽昗弨乿偵愝掕偟傑偡丅乮扐偟丄乽昗弨乿偵愝掕偟偰傕丄偲偰傕戝偒側悢帤傗偲偰傕彫偝側悢帤偼巜悢偱昞帵偝傟傑偡乯媡偵嫮惂揑偵巜悢偱昞帵偝偣偨偄偲偒偼丄僙儖偺昞帵宍幃傪乽巜悢乿偵巜掕偟傑偡丅
乮僙儖偺昞帵宍幃偼丄僙儖傪慖戰偟偰丄塃僋儕僢僋偟丄僙儖偺彂幃愝掕僔儑乕僩僇僢僩儊僯儏乕傪慖戰偟丄僙儖偺彂幃愝掕僟僀傾儘僌儃僢僋僗偱丄昞帵宍幃僞僽傪慖戰偟偰丄暘椶儃僢僋僗偱巜掕偟傑偡丅乯
俤倶們倕倢偺擖椡偲昞帵
|
抣
|
擖椡
|
昗弨昞帵
|
巜悢昞帵
|
|
係俉倠兌
|
48E3
|
48000
|
4.80E+04
|
|
侾侽侽倫俙
|
100E-12
|
1E-10
|
1.00E-10
|
|
係俈兪倁
|
47E-6
|
0.000047
|
4.70E-05
|
|
侽丏侽俀俀値俥
|
0.022E-9
|
2.2E-11
|
2.20E-11
|
俤倶們倕倢偱僆乕儉懃傪寁嶼偟偨椺傪帵偟傑偡丅傑偢丄壓昞偺傛偆偵抣傪巜悢傪巊偭偰擖椡偟傑偡丅偙偺椺偱偼丄侾峴栚偼尒弌偟偱偡丅俀峴栚傪巊偭偰丄侾倣倁傪侾侽侽倠兌偱妱偭偰丄棳傟傞揹棳傪媮傔偰偄傑偡丅
|
|
俙
|
俛
|
俠
|
俢
|
|
侾
|
揹埑侾倣倁
|
掞峈侾侽侽倠兌
|
揹棳偺抣乵俙乶
|
|
|
俀
|
1E-3
|
100E3
|
=A2/B2
|
|
俤倶們倕倢偼寢壥傪師偺傛偆偵帵偟傑偡丅
|
|
俙
|
俛
|
俠
|
俢
|
|
侾
|
揹埑侾倣倁
|
掞峈侾侽侽倠兌
|
揹棳偺抣乵俙乶
|
|
|
俀
|
1.00E-03
|
1.00E+05
|
1.00E-08
|
|
俛俀僙儖傪尒傞偲丄擖椡偟偨偲偍傝偵偼昞帵偝傟側偄帠偑暘傝傑偡丅乮100E3偲擖椡偟偨偗傟偳丄1.00E+5偲昞帵偝傟偰偄傞丄偳偪傜傕抣偼100000乯偮傑傝丄俤倶們倕倢偼擖椡偟偨宍幃傑偱偼妎偊偰偍傜偢丄擖椡偟偨抣傪妎偊偰偄傞偩偗偱偡丅
俠俀僙儖偵昞帵偝傟傞寁嶼寢壥1.00E-08乵俙乶偼丄偦偺傑傑偱偼暘偐傝擄偄抣偱偡丅偦偙偱丄乵値俙乶傪巊偭偰昞帵偝偣傑偡丅崁弶偺乽扨埵傪巜悢偱擖椡偡傞乿偺昞偵傛傟偽n乮僫僲乯偼E-9偱偟偨丅偱偡偐傜媡偵丄棁偺抣偵1E+9傪妡偗偰傗傟偽丄乵値俙乶偱昞帵偡傞偙偲偑偱偒傑偡丅偦偙偱丄師昞俢俀偺傛偆偵擖椡偟傑偡丅
|
|
俙
|
俛
|
俠
|
俢
|
|
侾
|
侾倣倁
|
侾侽侽倠兌
|
揹棳偺抣乵俙乶
|
揹棳偺抣乵値俙乶
|
|
俀
|
1E-3
|
100E3
|
=A2/B2
|
=C2*1E9
|
偡傞偲丄俤倶們倕倢偼師偺傛偆偵昞帵偟傑偡丅
|
|
俙
|
俛
|
俠
|
俢
|
|
侾
|
侾倣倁
|
侾侽侽倠兌
|
揹棳偺抣乵俙乶
|
揹棳偺抣乵値俙乶
|
|
俀
|
1.00E-03
|
1.00E+05
|
1.00E-08
|
1.00E+01
|
巜悢傪尦偵寁嶼偟偨偺偱丄俢侾僙儖偺昞帵宍幃傕帺摦揑偵巜悢偵愝掕偝傟偰偄傑偡丅俢侾僙儖偺昞帵宍幃傪昗弨偵愝掕偡傞偲丄師昞偺傛偆偵侾侽偲昞帵偝傟傑偡丅
|
|
俙
|
俛
|
俠
|
俢
|
|
侾
|
侾倣倁
|
侾侽侽倠兌
|
揹棳偺抣乵俙乶
|
揹棳偺抣乵値俙乶
|
|
俀
|
1.00E-03
|
1.00E+05
|
1.00E-08
|
10
|
偙偺傛偆偵丄棁偺抣偵丄扨埵偵懳墳偟偨巜悢偺丄俤偺屻偺晞崋傪媡偵偟偰妡偗傞偲丄偦偺扨埵偱昞偡偙偲偑偱偒傑偡丅偙偺傛偆側丄棁偺抣偵妡偗偰扨埵偱昞帵偡傞応崌偺巜悢傪師昞偵帵偟傑偡丅
棁偺抣傪扨埵偱昞帵偡傞
|
扨埵
|
f
|
p
|
n
|
兪
|
m
|
k
|
M
|
G
|
T
|
|
巜悢
|
1E15
|
1E12
|
1E9
|
1E6
|
1E3
|
1E-3
|
1E-6
|
1E-9
|
1E-12
|
仸乽扨埵傪巜悢偱擖椡偡傞乿偲偒偺昞偺丄E偺屻偺晞崋傪媡偵偟偨偩偗偱偡丅
仸俀侽侽俈埲崀偺俤倶們倕倢偱偼CONVERT娭悢傪巊偭偨曄姺傕壜擻偱偡丅
師昞偼丄尒弌偟偵婰嵹偺俀偮偺抣傪尦偵丄僆乕儉懃偱寁嶼偟偨抣傪帵偡昞偱偡丅椺偊偽丄尒弌偟偵懢榞偱帵偡侾俀倁偲俁兌偐傜僆乕儉懃偱寁嶼偟偨寢壥偑丄昞拞偵懢榞偱帵偡係俙偱偡丅
偙偺昞偵偼偄偔偮偐娫堘偄偑偁傝傑偡丅娫堘偭偰偄傞抣傪巜揈偟偰偔偩偝偄丅
|
|
12兪V
|
3k兌
|
12V
|
3兌
|
12mV
|
3M兌
|
|
4兪A
|
3兌
|
12mV
|
3M兌
|
12兪V
|
3k兌
|
12V
|
|
3M兌
|
4mA
|
|
4兪A
|
|
4nA
|
|
|
4A
|
3兪兌
|
12kV
|
3兌
|
12V
|
3m兌
|
12kV
|
|
3兌
|
4兪A
|
|
4A
|
|
4mA
|
|
|
4mA
|
3m兌
|
12V
|
3兌
|
12mV
|
3兌
|
12kV
|
|
3k兌
|
4nA
|
|
4mA
|
|
4兪A
|
|
壓昞偵丄岆傝偺偁傞抣傪壓慄偱帵偟傑偡丅
|
|
12兪V
|
3k兌
|
12V
|
3兌
|
12mV
|
3M兌
|
|
4兪A
|
3兌
|
12mV
|
3M兌
|
12兪V
|
3k兌
|
12V
|
|
3M兌
|
4mA
|
|
4兪A
|
|
4nA
|
|
|
4A
|
3兪兌
|
12kV
|
3兌
|
12V
|
3m兌
|
12kV
|
|
3兌
|
4兪A
|
|
4A
|
|
4mA
|
|
|
4mA
|
3m兌
|
12V
|
3兌
|
12mV
|
3兌
|
12kV
|
|
3k兌
|
4nA
|
|
4mA
|
|
4兪A
|
|
係. 埫嶼偲倣俙傗倠兌乮扨埵愙摢岅乯
偙偙偱偼俤倶們倕倢傪巊傢偢埫嶼偱扨埵傗僆乕儉懃傪巊偆曽朄傪愢柧偟傑偡丅俤倶們倕倢傪巊偭偰寁嶼傪孞傝曉偟偰偄傞偲丄帺慠偲偱偒傞傛偆偵側傝傑偡偑丄杮崁偺僐僣傪堄幆偡傞偙偲偱丄傛傝抁婜娫偱姷傟傞偙偲偑偱偒傑偡丅
傑偢丄悢帤摨巑寁嶼偟丄師偵偙傟偲偼暿偵丄扨埵摨巑傪寁嶼偟傑偡丅俤倶們倕倢傪巊偆曽朄偱傕巊梡偟偨丄奺扨埵偺忔悢傪壓昞偵帵偟傑偡丅
庡側扨埵愙摢岅偲偦偺忔悢
|
扨埵
|
f
|
p
|
n
|
兪
|
m
|
k
|
M
|
G
|
T
|
|
忔悢
|
(-15)
|
(-12)
|
(-9)
|
(-6)
|
(-3)
|
(3)
|
(6)
|
(9)
|
(12)
|
偨偲偊偽丄10kV偱2mA棳傟偨応崌丄掞峈偼僆乕儉懃偱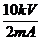 偲寁嶼偟偰媮傔傑偡偑丄傑偢悢帤偩偗偵拲栚偟偰丄
偲寁嶼偟偰媮傔傑偡偑丄傑偢悢帤偩偗偵拲栚偟偰丄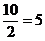 偲寁嶼偟丄師偵扨埵偩偗傪
偲寁嶼偟丄師偵扨埵偩偗傪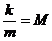 偲寁嶼偟偰丄椉幰傪崌傢偣偰5M兌偲摎傪弌偟傑偡丅
偲寁嶼偟偰丄椉幰傪崌傢偣偰5M兌偲摎傪弌偟傑偡丅
忋偱巊梡偟偨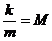 摍偺乽扨埵偺寁嶼乿偼帺慠偲妎偊傑偡偑丄姷傟傞傑偱偼丄忔悢偱寁嶼偟傑偡丅崱夞偺椺偱偼壓恾偺傛偆偵丄
摍偺乽扨埵偺寁嶼乿偼帺慠偲妎偊傑偡偑丄姷傟傞傑偱偼丄忔悢偱寁嶼偟傑偡丅崱夞偺椺偱偼壓恾偺傛偆偵丄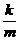 傪
傪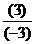 偲峫偊丄暘曣偺(-3)偺晞崋偼斀揮偟偰(+3)偐傜崌嶼偟偰丄(6)=M偲峫偊傑偡丅
偲峫偊丄暘曣偺(-3)偺晞崋偼斀揮偟偰(+3)偐傜崌嶼偟偰丄(6)=M偲峫偊傑偡丅
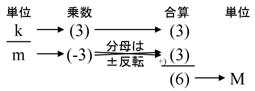
暿偺椺偲偟偰丄3k兌亊4兪A 偺応崌側傜丄悢帤偺晹暘偼乽3亊4乿偱12偱偡丅扨埵偺晹暘偼乽k亊兪亖m乿偱偡偐傜乮妎偊傞傑偱偼 (3)+(-6) = (-3) = m偲峫偊傞乯3k兌亊4兪A=12mA偲埫嶼偱偒傑偡丅
嶲峫傑偱偵昿搙偺崅偄扨埵偺寁嶼傪師昞敀怓晹偵帵偟傑偡丅傕偪傠傫堄幆偡傞偩偗偱椙偄偺偱丄壓昞傪埫婰偡傞昁梫偼偁傝傑偣傫丅
扨埵偺寁嶼乮僌儗乕偺棑偼偁傑傝巊傢側偄乯
俆. 夞楬恾偺昤偒曽
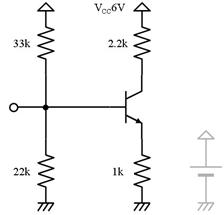
揹巕宯偺夞楬恾偱偼丄揹尮偲僌儔僂儞僪偺攝慄偼婰崋偱昞偟丄揹尮乮揹抮儅乕僋乯偼婰擖偟側偄応崌偑戝敿偱偡丅偨偲偊偽丄楙廗偱搊応偟偨壓恾乮倎乯偺夞楬偼丄壓恾乮倐乯偺傛偆偵娙慺偵昤偐傟傑偡丅
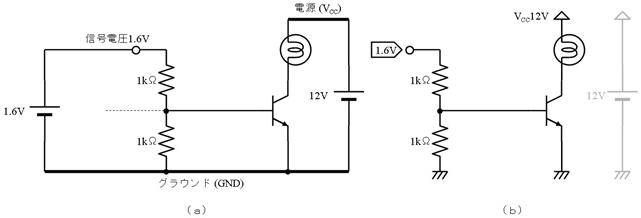
傑偨丄揹埑偑崅偄晹暘掱丄夞楬恾偺忋晹偵昤偔偲乮夞楬恾偼戝偒偔側傝傑偡偑乯夞楬偑撉傒堈偔側傝傑偡丅
俆.侾. 楙廗
壓恾偺夞楬恾傪丄尒堈偔彂偒捈偟偰偔偩偝偄丅
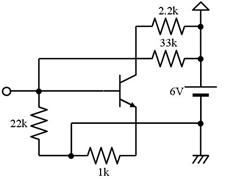
俆.俀. 摎
俇. 夞楬恾偵揹棳傗揹埑傪彂偒崬傓
夞楬恾傪撉傓偲偒偼丄揹棳傗揹埑傪彂偒崬傒側偑傜撉傒傑偡丅杮彂偱偼丄揹棳偼栴報  偱丄揹埑偼怟旜偵朹偺偮偄偨栴報
偱丄揹埑偼怟旜偵朹偺偮偄偨栴報  偱帵偟傑偡丅
偱帵偟傑偡丅
彯丄揹埑傪椉栴報  偱帵偡曽朄傕偁傝傑偡偑丄偙偺曽朄偱偼揹埑偺曽岦偑暘傜側偄偺偱丄杮彂偱偼巊偄傑偣傫丅
偱帵偡曽朄傕偁傝傑偡偑丄偙偺曽朄偱偼揹埑偺曽岦偑暘傜側偄偺偱丄杮彂偱偼巊偄傑偣傫丅
杮彂偱偼丄岎棳偲捈棳傪堦偮偺夞楬偵帵偡昁梫偑偁傞応崌丄捈棳傪幚慄  偱丄岎棳傪揰慄
偱丄岎棳傪揰慄 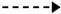 偱帵偟傑偡丅
偱帵偟傑偡丅
俈. 捈楍崌惉掞峈
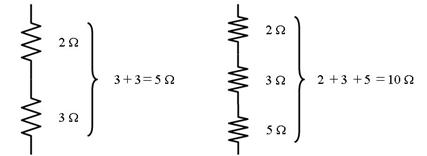
暋悢偺掞峈傪愙懕偟偰摼傜傟傞掞峈抣傪丄崌惉掞峈偲屇傃傑偡丅捈楍偵愙懕偟偨応崌偼捈楍崌惉掞峈偱丄偦偺掞峈抣偼丄奺掞峈偺榓偱媮傔傞偙偲偑偱偒傑偡丅
俉. 暘埑
壓恾偵帵偡傛偆偵丄捈楍偵愙懕偟偨奺掞峈偵偼丄掞峈抣偵斾椺偟偨揹埑偑敪惗偟傑偡丅
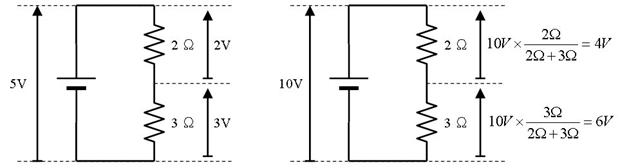
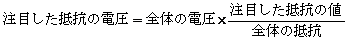
暘埑偱丄3.3k偺椉抂偵摼傜傟傞揹埑傪媮傔偰偔偩偝偄丅
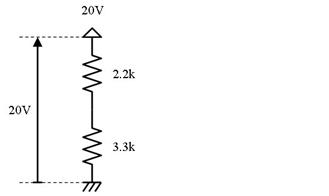
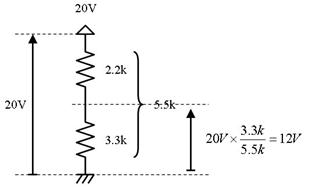
俋. 僉儖僸揹棳懃乮僉儖僸儂僢僼偺戞侾朄懃乯
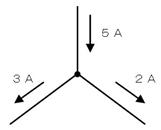
壓恾偺傛偆偵丄夞楬忋偺堦揰偐傜棳傟弌偡揹棳偺崌寁乮俁俙亄俀俙乯偼丄棳傟崬傓揹棳偺崌寁乮俆俙乯偲摨偠偵側傝傑偡丅
侾侽. 僉儖僸揹埑懃乮僉儖僸儂僢僼偺戞俀朄懃乯
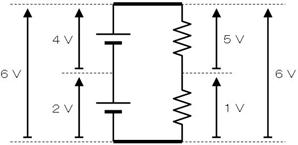
壓恾偺傛偆偵屳偄偵乮懢慄晹偱乯愙懕偝傟偨俀偮偺夞楬偱偼丄嵍塃偺揹埑偑摨偠偵側傞乮嵍俇倁丄塃俇倁乯偲偄偆朄懃偱偡乮偁偨傝傑偊偱偡偹乯丅乽奺晹昳偺揹埑傪崌寁偡傞偲丄慡懱偺揹埑偵側傞乿朄懃偲峫偊傞偙偲傕偱偒傑偡丅乮嵍懁偑係倁亄俀倁亖俇倁丄塃懁偑俆倁亄侾倁亖俇倁乯
偙偺傛偆偵僉儖僸偵偼揹棳懃偲揹埑懃偑偁傝傑偡偑丄杮彂偱扨偵乽僉儖僸懃乿偲尵偭偨応崌偼丄僉儖僸揹棳懃傪巜偟傑偡丅僉儖僸揹埑懃偼堄幆偣偢偵巊偊傞応崌偑懡偄偱偡丅
侾侽.侾. 楙廗
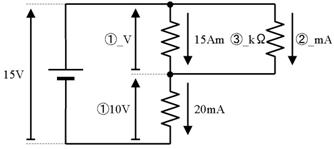
壓恾偺夞楬偺丄嘆乣嘊偺揹埑丄揹棳丄掞峈丄傪媮傔偰壓偝偄丅
|
斣崋
|
摎
|
僸儞僩
|
|
嘆
|
V
|
僉儖僸揹埑懃傪巊梡
|
|
嘇
|
mA
|
僉儖僸揹棳懃傪巊梡
|
|
嘊
|
k兌
|
僆乕儉懃傪巊梡
|
侾侽.俀. 摎
|
斣崋
|
摎
|
愢柧
|
|
嘆
|
俆倁
|
僉儖僸揹埑懃傛傝丄侾俆倁偲侾侽倁偺嵎偱俆倁
|
|
嘇
|
俆倣俙
|
僉儖僸揹棳懃傛傝丄俙揰偵拲栚偟偰丄俀侽倣俙偲侾俆倣俙偺嵎偱俆倣俙
|
|
嘊
|
侾倠兌
|
僆乕儉懃傛傝丄俆倁偱侾倣俙偩偐傜侾倠兌
|
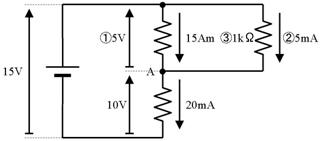
侾侽.俁. 楙廗
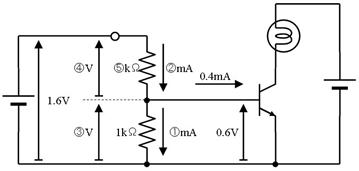
壓恾偺夞楬偺丄嘆乣嘍偺揹埑丄揹棳丄掞峈丄傪媮傔偰壓偝偄丅
|
斣崋
|
摎
|
僸儞僩
|
|
嘆
|
倣俙
|
僆乕儉懃傪巊梡
|
|
嘇
|
倣俙
|
僉儖僸揹棳懃傪巊梡
|
|
嘊
|
倁
|
僉儖僸揹埑懃傪巊梡
|
|
嘋
|
倁
|
僉儖僸揹埑懃傪巊梡
|
|
嘍
|
倠兌
|
僆乕儉懃傪巊梡
|
侾侽.係. 摎
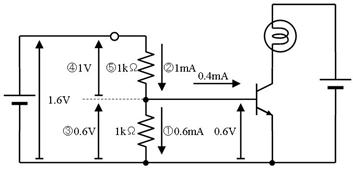
|
斣崋
|
摎
|
愢柧
|
|
嘆
|
侽丏俇倣俙
|
僆乕儉懃傛傝丄侾倠兌偵侽丏俇倁偑壛傢偭偰丄侽丏俇倣俙
|
|
嘇
|
侾倣俙
|
僉儖僸揹棳懃傛傝丄棳傟弌偡揹棳偑侽丏俁倣俙偲侽丏俇倣俙偩偐傜丄棳傟崬傓揹棳偼侾倣俙
|
|
嘊
|
侽丏俇倁
|
僉儖僸揹埑懃傛傝丄侽丏俇倁
|
|
嘋
|
侾倁
|
僉儖僸揹埑懃傛傝丄嘊偺侽丏俇倁偲嘋傪壛偊傞偲丄侾丏俇倁偲側傞偐傜丄侾倁
|
|
嘍
|
侾倠兌
|
僆乕儉懃傛傝丄侾倁偱侾倣俙棳傟傞偐傜丄侾倠兌
|
侾侾. 掞峈偲僐儞僟僋僞儞僗
掞峈偼乽揹棳偺棳傟擄偝乿偱偡偑丄僐儞僟僋僞儞僗偼乽揹棳偺棳傟堈偝乿偱偡丅壓昞偵乽抣偺椺乿偱帵偡傛偆偵丄掞峈偺抣偑彫偝偄掱丄僐儞僟僋僞儞僗偺抣偼戝偒偔側傝傑偡丅偮傑傝丄掞峈偲僐儞僟僋僞儞僗偺抣偵偼乽媡悢乿偺娭學偑偁傝傑偡丅
|
柤慜
|
掞峈
乮儗僕僗僞儞僗乯
|
僐儞僟僋僞儞僗
|
|
僀儊乕僕
|
揹棳偺棳傟擄偝
|
揹棳偺棳傟堈偝
|
|
扨埵
|
兌
|
|
俽
|
|
扨埵偺撉傒
|
OHM
僆乕儉
|
MHO
儌乕
|
SEMENS
僕乕儊儞僗
|
|
抣偺椺
|
係兌
|
侾乛係俽
|
|
侾兌
|
侾俽
|
|
侾乛係兌
|
係俽
|
忋昞偵偁傞偲偍傝丄僐儞僟僋僞儞僗偺扨埵偼乮 偲俽偺乯俀偮偁傝傑偡丅兌乮俷俫俵乯偺媡悢偑
偲俽偺乯俀偮偁傝傑偡丅兌乮俷俫俵乯偺媡悢偑  乮俵俫俷乯偲偄偆偺偼丄偍拑栚偱妎偊堈偄偨傔丄惀旕巊偄偨偄偺偱偡偑丄
乮俵俫俷乯偲偄偆偺偼丄偍拑栚偱妎偊堈偄偨傔丄惀旕巊偄偨偄偺偱偡偑丄 偲偄偆暥帤偑柍偄偨傔丄杮彂偱偼俽乮僕乕儊儞僗乯傪巊偄傑偡丅
偲偄偆暥帤偑柍偄偨傔丄杮彂偱偼俽乮僕乕儊儞僗乯傪巊偄傑偡丅
堦杮偺掞峈婍傪乽棳傟擄偝兌乿偱屇傫偱傕丄乽棳傟堈偝俽乿偱屇傫偱傕偐傑偄傑偣傫丅偮傑傝丄晹昳揦偱係兌偺掞峈傪峸擖偡傞帪偵乽係暘偺侾僕乕儊儞僗偺掞峈傪壓偝偄乿偲尵偭偰傕椙偄栿偱偡丅偱偡偐傜乽掞峈乮兌乯偑偁傟偽丄僐儞僟僋僞儞僗乮俽乯側傫偰梫傜側偄偲傗乿偲巚偄彑偪偱偡偑丄幚偼偙偺僐儞僟僋僞儞僗丄暲楍夞楬偱偲偰傕栶偵棫偪傑偡丅
侾俀. 暲楍崌惉掞峈
捈楍崌惉掞峈偼崌寁偡傞偩偗偱媮傔傞偙偲偑偱偒傑偟偨偑丄暲楍崌惉掞峈偼偪傚偭偲柺搢偱偟偨丅偦偙偱僐儞僟僋僞儞僗乮捠傝傗偡偝乯傪巊偭偰峫偊偰傒傑偡丅僐儞僟僋僞儞僗傪巊偆偲暲楍夞楬偼崌寁偡傞偩偗偱寁嶼偱偒傑偡丅
壓恾偺夞楬偱偼丄捠傝傗偡偝俀俽偲俁俽偺掞峈偑暲楍偵愙懕偝傟偰偄傑偡丅摴楬偵歡偊傟偽丄摴暆俀倣偲丄俁倣偺丄俀杮偺摴楬偱栚揑抧偵宷偑偭偰偄傞忬懺偱偡丅偱偡偐傜丄俀杮偺摴楬傪崌傢偣偰丄摴暆俆倣偺摴偲摨偠偩偗偺恖偑捠傟傞敜偱偡丅
夞楬偵榖傪栠偡偲丄捠傝傗偡偝俀俽偺掞峈偲俁俽偺掞峈偑暲楍側偺偱丄暲楍偵偟偨捠傝傗偡偝偼俆俽偲側傝傑偡丅偙偺傛偆偵丄僐儞僟僋僞儞僗乮棳傟堈偝乯傪崌寁偡傞偩偗偱丄暲楍夞楬偺寁嶼偑偱偒傑偟偨丅摎偊傪兌偱弌偟偨偄応崌偼丄俆俽偺媡悢傪媮傔偰丄侽丏俀兌偲側傝傑偡丅
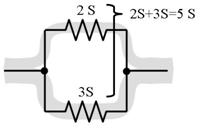
偝偰丄忋恾偱偼掞峈偺巇條偑丄棳傟堈偝乮僐儞僟僋僞儞僗丗俽丗僕乕儊儞僗乯偱帵偝傟偰偄傑偟偨丅師偵丄掞峈偑偄偮傕捠傝丄棳傟擄偝乮掞峈丗兌乯偱帵偝傟偰偄傞応崌傪峫偊傑偡丅
壓恾偺夞楬偱偼丄侾兌偲係兌偑暲楍偵愙懕偝傟偰偄傑偡丅偦傟偧傟偺掞峈抣傪丄棳傟堈偝偵彂偒捈偡偲丄侾俽偲侽丏俀俆俽偱偡丅棳傟堈偝傪崌寁偟偰丄暲楍愙懕偺棳傟堈偝乮暲楍崌惉僐儞僟僋僞儞僗乯傪寁嶼偡傞偲丄侾丏俀俆俽偱偡丅摎偊傪棳傟擄偝乮兌乯偱弌偟偨偄応崌偼丄侾丏俀俆俽偺媡悢傪媮傔偰丄暲楍崌惉掞峈偼侽丏俉兌偲側傝傑偡丅
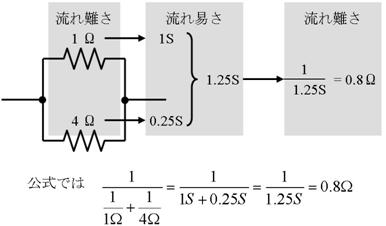
忋恾偺壓晹偵暲楍崌惉掞峈傪岞幃偱媮傔傞曽朄傪帵偟傑偡丅幚偼岞幃偺曽朄傕丄俀偮偺掞峈抣傪僐儞僟僋僞儞僗偵曄姺偟偰偐傜崌寁偟丄崌寁偱摼偨僐儞僟僋僞儞僗傪丄傕偆堦搙掞峈抣偵栠偟偰偄傞丄偲暘傝傑偡丅
暲楍掞峈偺寁嶼偼師偺傛偆偵彂偔応崌偑偁傝傑偡丅
侾兌丂乛乛丂係兌丂亖丂侽丏俉兌
乽乛乛乿偼暲楍偺掞峈抣傪寁嶼偡傞丄偲偄偆婰崋偱偡丅
侾俀.侾. 楙廗
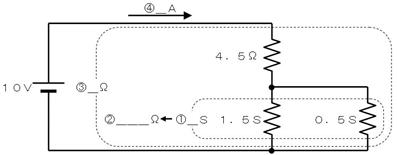
壓恾偺夞楬偺嘆乣嘋偺僐儞僟僋僞儞僗丄掞峈丄揹棳傪夞楬恾撪偵婰擖偟偰偔偩偝偄丅
侾俀.俀. 摎
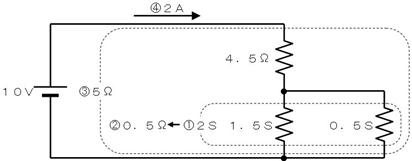
嘆侽丏俆俽偲侾丏俆俽偑暲楍側偺偱丄俀俽
嘇俀俽傪媡悢偵偟偰丄侽丏俆兌
嘊係丏俆兌偲侽丏俆兌偑捈楍側偺偱俆兌
嘋俆兌偵侾侽倁偑壛傢偭偰偄傞偺偱丄俀俙
侾俁. 暘棳偺朄懃
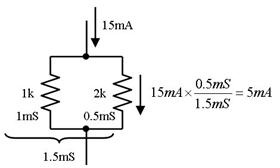
捈楍掞峈偵暘埑偺峫偊曽偑偁傞傛偆偵丄暲楍掞峈偵偼暘棳偺峫偊曽偑偁傝傑偡丅壓恾偵帵偡傛偆偵丄暲楍偵愙懕偟偨奺掞峈偵偼丄僐儞僟僋僞儞僗乮棳傟堈偝乯偵斾椺偟偨揹棳偑棳傟傑偡丅
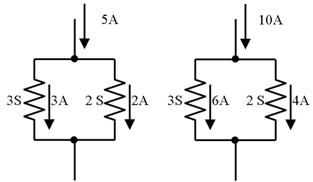
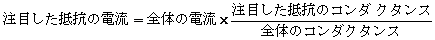
壓恾偺夞楬偱丄2k兌偵棳傟傞揹棳傪夞楬恾撪偵婰擖偟偰壓偝偄丅
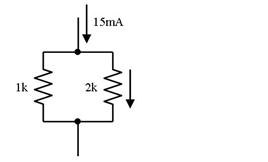
侾係. 拞揰偺揹埑
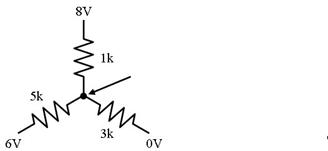
壓恾偵帵偡丄俁偮偺揹埑偵宷偑偭偨丄俁杮偺掞峈偺拞揰偺揹埑偼丄僉儖僸懃偱楢棫曽掱幃棫偰側偔偰傕丄恾拞偺岞幃偱媮傔傞偙偲偑偱偒傑偡丅偙偺岞幃偼堦尒暋嶨偦偆偱偡偑丄婯懃惈偑偁傞偺偱妝偵妎偊傜傟傑偡丅
戝暥帤ABC偑揹埑丄彫暥帤abc偼掞峈抣偱偡丅傑偨丄Abc偼A亊b亊c偺帠偱偡丅乮偮傑傝丄亊偼徣棯偡傞応崌偑偁傝傑偡乯
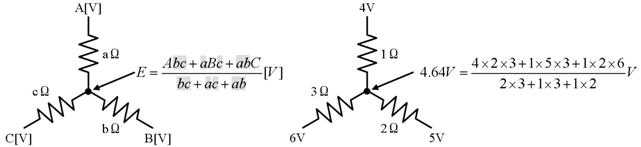
掞峈偑係杮丄俆杮偲憹偊偨応崌偼偦傟偧傟師偺傛偆偵側傝傑偡丅
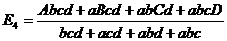
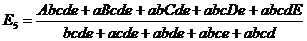
壓恾偺夞楬偵栴報偱帵偡揰偺揹埑傪媮傔偰偔偩偝偄丅
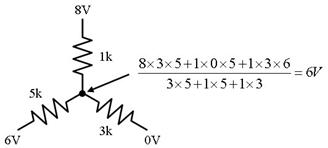
侾. 揹棳偲揹壸
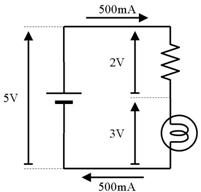
壓恾嵍懁偺憰抲偼丄億儞僾偱悈傪憲傝丄侾昩娫偵俁俴乮儕僢僩儖乯偺悈傪弞娐偝偣偰偄傑偡丅棳傟傞悈偺検偼俁俴乛昩偱偡丅幹岥傪挱傔偰偄傞偲丄侾昩偁偨傝俁俴偺悈偑捠夁偡傞偺偑尒偊傑偡丅
偝偰丄乽悈偺検乿丗俴乮儕僢僩儖乯偵憡摉偡傞揹婥偺検傪乽揹壸乿丗俠乮僋乕儘儞乯偲屇傃傑偡丅壓恾塃偺夞楬偱偼丄侾昩娫偵俁俠乮僋乕儘儞乯偺揹壸偑捠夁偟偰偄傑偡丅偮傑傝丄俁俠乛昩偱偡丅巹偨偪偼丄偙傟傪俁俙偲屇傫偱偄傑偡丅乮偮傑傝丄俁俙
亖 俁俠乛昩偱偡乯
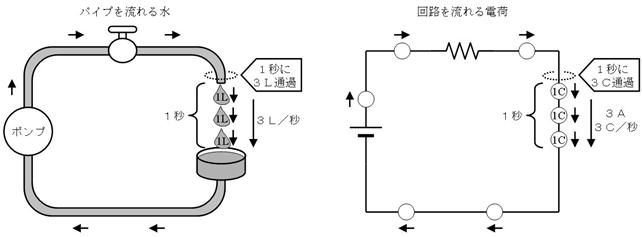
枅昩俁俴偱俆昩娫棳傟傞偲丄侾俆俴偺悈偑捠夁偟傑偡丅偙傟偲摨條偵丄枅昩俁俠乮俁俠乛昩亖俁俙乯偑俆昩娫棳傟傞偲丄侾俆俠偺揹壸偑捠夁偟傑偡丅偮傑傝丄
捠夁偟偨揹壸乵俠乶亖揹棳乵俙乶亊帪娫乵昩乶
偱偡丅
侾.侾. 楙廗
俆兌偺掞峈偵侾侽倁傪壛偊傞偲丄侾暘娫偱壗僋乕儘儞偺揹壸偑捠夁偟傑偡偐丅
侾.俀. 摎
僆乕儉懃傛傝丄揹棳偼侾侽倁亐俆兌亖俀俙丅侾暘偼俇侽昩偩偐傜丄揹壸偼俀俙亊俇侽昩亖侾俀侽俠捠夁偡傞丅
俀. 僐儞僨儞僒
僐儞僨儞僒偼壓恾偺僐僢僾偑悈傪拁偊傞傛偆偵丄揹壸傪拁偊傞晹昳偱偡丅
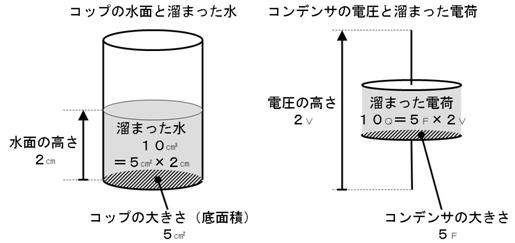
僐僢僾偱偼悈柺偺崅偝偲僐僢僾偺戝偒偝乮掙柺愊乯傪妡偗傞偲棴傑偭偨悈偺検傪抦傞偙偲偑偱偒傑偡丅忋恾偺椺偱偼丄
僐僢僾偺戝偒偝乮掙柺愊乯俆們倣俀丂亊丂悈柺偺崅偝俀們倣丂亖丂悈偺検侾侽們倣俁
偲側傝傑偡丅僐儞僨儞僒偱傕摨條偵丄棴傑偭偰偄傞揹壸偼丄揹埑偺崅偝偲僐儞僨儞僒偺戝偒偝乮梕検乯傪妡偗偰媮傔傞偙偲偑偱偒傑偡丅
僐儞僨儞僒偺戝偒偝乮梕検乯俆俥丂亊丂揹埑偺崅偝俀倁丂亖丂揹壸偺検侾侽俠
傕偟偙偺僐僢僾偵丄枅昩侾們倣俁偺惃偄偱丄侾侽昩娫悈傪拲偖偲偲丄悈柺偑俀們倣偵忋徃偟傑偡偐傜丄
悈偺惃偄侾們倣俁乛昩丂亊丂侾侽昩丂乛丂僐僢僾偺戝偒偝俆們倣俀丂亖丂悈柺偺崅偝俀們倣丂
偲側傝傑偡丅悈偺惃偄侾們倣俁乛昩偼丄揹棳侾俠乛昩乮偮傑傝丄侾俙乯偺偙偲偱偡偐傜丄僐儞僨儞僒偱偼丄揹棳偲帪娫傪妡偗偰乮棳傟崬傫偩揹壸傪媮傔偰乯梕検偱妱傟偽丄忋徃偟偨揹埑偑寁嶼偱偒傑偡丅
揹棳侾俙丂亊丂帪娫侾侽昩丂乛丂梕検俆俥丂亖丂揹埑偺崅偝乮憹壛乯俀倁
俀.侾. 楙廗
嘆侾俀俥偺僐儞僨儞僒偵丄俀俙偺揹棳偱侾暘娫廩揹偟傑偟偨丅乮僐儞僨儞僒偵揹棳傪棳偟崬傫偱偰丄揹壸傪挋傔傞偙偲傪廩揹偡傞偲尵偄傑偡乯僐儞僨儞僒偵棴傑偭偨揹壸偼壗僋乕儘儞偱偡偐丅僐儞僨儞僒偼壗儃儖僩偵廩揹偝傟傑偡偐丅
嘇侾侽侽兪俥偺僐儞僨儞僒偑俀侽倁偵廩揹偝傟偰偄傑偡丅堦掕偺揹棳侾倣俙偱曻揹乮僐儞僨儞僒偐傜揹棳傪棳傟弌偝偣丄僐儞僨儞僒偵棴傑偭偰偄傞揹壸傪揻偒弌偝偣傞偙偲傪丄曻揹偲尵偄傑偡乯偝偣傟偽丄壗昩偱嬻乮僐儞僨儞僒偺揹壸偑側偔側傞乯偵側傝傑偡偐丅
俀.俀. 摎
嘆侾暘偼俇侽昩偩偐傜丄棴傑偭偨揹壸偼俀俙亊俇侽昩亖侾俀侽俠丅侾俀俥偺僐儞僨儞僒偵侾俀侽俠偑拁偊傜傟傞偲丄揹埑偼侾侽倁偲側傞丅
嘇僐儞僨儞僒偵棴傑偭偰偄傞揹壸偼丄侾侽侽兪俥亊俀侽倁偱俀倣俠偱偁傞丅侾倣俙偲偼丄侾倣俠乛昩偺偙偲偩偐傜丄俀倣俠亐侾倣俠乛昩亖俀昩偱僐儞僨儞僒偑嬻偵側傞丅
俁. 俠俼夞楬偺曻揹
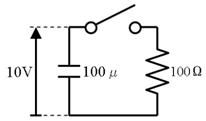
壓恾偺夞楬偱偼僐儞僨儞僒偼嵟弶俉倁偵廩揹偝傟偰偄傑偡丅偙偙偱丄俽倂傪俷俶偵偡傞偲丄侾兌偺掞峈傪捠偠偰丄僐儞僨儞僒偑曻揹乮僐儞僨儞僒偵棴傑偭偨揹壸偑揹棳偱棳傟弌偡乯傪巒傔傑偡丅
俽倂傪俷俶偟偨弖娫丄壓恾夞楬恾偺嘆偺傛偆偵丄掞峈偵偼俉倁偑妡偐傝俉俙偺揹棳偑棳傟傑偡丄偦偺寢壥丄僌儔僼偵嘆偱帵偡傛偆偵丄僐儞僨儞僒偺揹壸偼俉俙偺惃偄偱曻揹偟丄懍傗偐偵揹埑偑壓偑傝巒傔傑偡丅
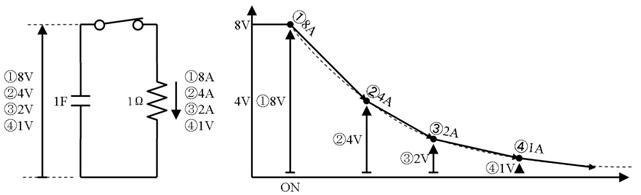
僐儞僨儞僒偑係倁傑偱曻揹偡傞偲丄忋恾嘇偺傛偆偵丄曻揹揹棳偑係俙偵尭彮偟丄曻揹偺惃偄偑庛傑傝傑偡丅偙偺傛偆偵師戞偵惃偄傪庛傔側偑傜曻揹偑懕偒丄椺偊偽丄侾倁傑偱曻揹偡傞偲丄忋恾嘋偺傛偆偵丄曻揹揹棳偼侾俙偵尭彮偟丄曻揹偺惃偄偼嬌傔偰備傞傗偐偵側傝傑偡丅
偙偺傛偆偵僐儞僨儞僒偵掞峈傪愙懕偡傞偲丄揹埑偑掅壓偡傞偲丄曻揹偡傞揹棳傕尭彮偡傞偨傔丄忋恾偺僌儔僼偵揰慄偱帵偡傛偆偵丄師戞偵惃偄傪庛傜偣側偑傜丄曻揹偟偰峴偒傑偡丅
壓恾偵曻揹偺條巕傪娙慺偵帵偟傑偡丅僐儞僨儞僒偺梕検偑俠乵俥乶丆掞峈偑俼乵兌乶偺応崌丄壓恾偵揰慄偱帵偡傛偆偵妸傜偐偵曻揹偟傑偡丅
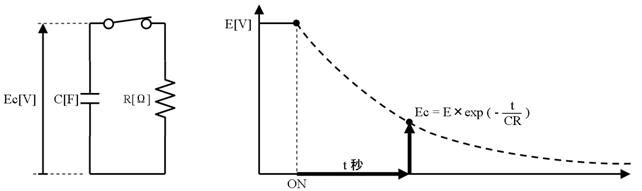
僐儞僨儞僒偺嵟弶偺揹埑偑俤乵倁乶偺応崌丄僗僀僢僠俷俶偐傜倲昩屻偺僐儞僨儞僒偺揹埑俤們偼丄師偺幃偱寁嶼偱偒傑偡丅乮exp偼師戞偵惃偄傪庛傜偣傞乮嫮傔傞乯條巕傪寁嶼偡傞娭悢偱偡丅乯
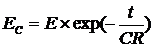 仼偙偺幃偼暘傜側偔偰傕椙偄
仼偙偺幃偼暘傜側偔偰傕椙偄
俤倶們倕倢偱偼丄=E1*EXP(-T1/C1/R1)偱寁嶼偱偒傑偡丅
丂E1=嵟弶偺揹埑乵倁乶丄T1=帪娫乵昩乶丄C1=僐儞僨儞僒偺梕検乵俥乶丄R1=掞峈抣乵兌乶
偨偲偊偽丄偨偲偊偽丄侾侽兪僐儞僨儞僒傪侾侽侽倁偵廩揹偟偰丄侾侽侽倠兌偱侾昩曻揹偟偨応崌偼丄俤倶們倕倢偵=100*EXP(-1/10E-6/100E3)偲擖椡偟偰丄栺俁俈倁傑偱揹埑偑壓偑傞偲寁嶼偱偒傑偡丅
媡偵丄僐儞僨儞僒偑強掕偺揹埑偵曻揹偡傞傑偱偺帪娫傪寁嶼偡傞偙偲傕偱偒傑偡丅乮ln偼exp偺媡偺摥偒傪偡傞娭悢偱偡丅乯
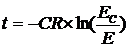 仼偙偺幃偼暘傜側偔偰傕椙偄
仼偙偺幃偼暘傜側偔偰傕椙偄
俤倶們倕倢偱偼丄=-C1*R1*ln(E2/E1)偱寁嶼偱偒傑偡丅
丂E1=嵟弶偺揹埑乵倁乶丄E2=強掕偺揹埑乵倁乶丄C1=僐儞僨儞僒偺梕検乵俥乶丄R1=掞峈抣乵兌乶
偨偲偊偽丄侾侽兪偺僐儞僨儞僒傪侾侽侽倁偵廩揹偟偰丄侾侽侽倠兌偱曻揹偟偰俇侽倁偵揹埑偑壓偑傞傑偱偺帪娫偼丄俤倶們倕倢偵=-10E-6*100E3*LN(60/100)偲擖椡偟偰丄栺侽丏俆侾昩偲寁嶼偱偒傑偡丅
俁.侾. 楙廗
俤倶們倕倢傪梡偄偰丄壓恾偺夞楬偺僗僀僢僠傪俷俶偵偟偨屻偺曻揹偺條巕傪侾侽倣昩枅偵寁嶼偟丄僌儔僼偵帵偟偰偔偩偝偄丅
俁.俀. 摎
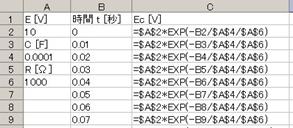
俤倶們倕倢偵壓恾偺傛偆偵擖椡偟傑偡丅A2丄A4丄A6偺僙儖偼愨懳嶲徠側偺偱丄俥係僉乕傪墴偟偰丄$A$4摍偲偟傑偡丅
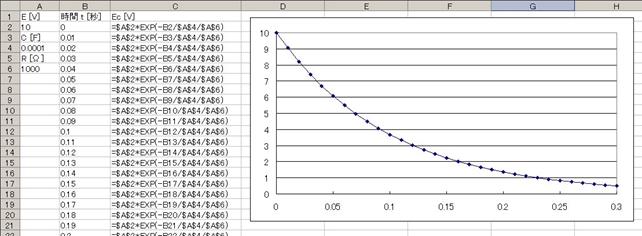
寁嶼偝偣丄僌儔僼傪昞帵偝偣傞偲丄壓恾偺傛偆偵側傝傑偡丅
係. 帪掕悢冄
帪掕悢偼丄偠偰偄偡偆丄偲偒偰偄偡偆丄偲偒偠傚偆偡偆丄偲撉傒曽偑條乆偵偁傝傑偡偑丄偳傟傕惓偟偄偲偝傟偰偄傑偡丅婰崋偼冄乮僞僂乯偱偡丅
俠俼夞楬偼嵟弶偼惃偄椙偔曻揹傪奐巒偟丄師戞偵曻揹偺惃偄傪庛傔偰峴偒傑偡偑丄乽帪掕悢冄乿偼壓恾偺僌儔僼偵懢偄揰慄偱帵偡傛偆偵丄乽傕偟丄嵟弶偺惃偄偺傑傑曻揹偟懕偗偨傜丄壗昩偱曻揹偑廔椆偡傞偐乿傪昞偟偰偄傑偡丅曻揹偺僌儔僼傪庤偱彂偔偲偒偵丄偙偺帪娫冄偑暘傞偲曋棙偱偡丅
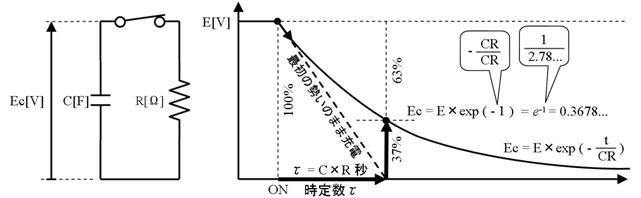
冄偺抣偼丄俠偲俼傪妡偗偰媮傔傞帠偑偱偒傑偡丅
冄乵昩乶
亖 俠乵俥乶亊俼乵兌乶
偝傜偵丄嵟弶偺揹埑傪侾侽侽倁偲偟偰丄僗僀僢僠傪俷俶偵偟偰偐傜冄乮亖俠亊俼乯昩宱夁偟偨偲偒偺僐儞僨儞僒偺揹埑傪寁嶼偡傞偲丄
侾侽侽
亊 倕倶倫乮亅俠俼乛俠俼乯亖
俤 亊 倕倶倫乮亅侾乯亖
栺俁俈
俤倶們倕倢偱偼=100*EXP(-1)偱36.78乧偲昞帵偝傟傞丅
偲側傝丄冄昩宱偮偲丄僐儞僨儞僒偺揹埑偼嵟弶偺俁俈亾傑偱掅壓偟傑偡丅乮偝傜偵冄昩宱偮偲丄偝傜偵偦偺俁俈亾傑偱掅壓偟丄偙傟傪孞傝曉偟偰曻揹偟偰峴偒傑偡丅乯偙偺傛偆偵帪掕悢偺抣偼丄夞楬偺摦嶌傪挷傋傞偺偵偲偰傕栶偵棫偪傑偡丅
僐儞僨儞僒梕検[俥]偲掞峈[兌]傪妡偗傞偲丄帪娫[昩]偑媮傑傞偺偼丄婏柇側姶偠偱偡偑丄梕検亖揹壸乛揹埑傑偨丄揹壸亖揹棳亊帪娫偱偁傞偙偲偐傜丄師偺傛偆偵峫偊傞偙偲偑偱偒傑偡丅
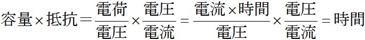
係.侾. 楙廗
愭偺楙廗栤戣乮俠亖侾侽侽兪俥丄俼亖侾倠兌乯偺夞楬偺帪掕悢冄傪媮傔丄曻揹奐巒偐傜冄昩屻偺僐儞僨儞僒偺揹埑傪楙廗栤戣偺摎偺僌儔僼偐傜媮傔偰偔偩偝偄丅嵟弶偺揹埑偺壗亾偵掅壓偟偰偄傑偡偐丠
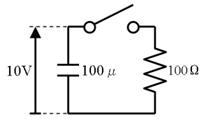
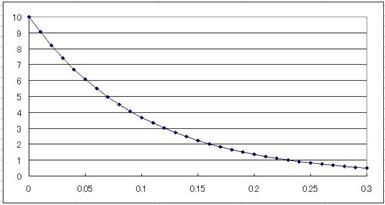
帪掕悢冄丂丂丂丂倣昩丂僌儔僼偐傜媮傔偨揹埑丂丂丂丂倁丂揹埑偺妱崌丂丂丂丂亾
係.俀. 摎
帪掕悢冄亖侾侽侽兪俥亊侾倠兌亖侾侽侽倣昩
帪掕悢冄丂侾侽侽倣昩丂僌儔僼偐傜媮傔偨揹埑丂俁丏俈倁丂揹埑偺妱崌丂丂俁俈亾
俆. 俠俼夞楬偺廩揹
壓恾嵍懁偺夞楬偱僗僀僢僠傪俷俶偵偡傞偲丄掞峈傪捠偟偰揹棳偑棳傟丄僐儞僨儞僒偑廩揹偝傟偰峴偒傑偡丅
傑偨丄壓恾塃懁偵帵偡偲偍傝丄僐儞僨儞僒曻揹偺僌儔僼傪忋壓媡偵偡傞偲丄崱夞偺僐儞僨儞僒廩揹偺僌儔僼偵側傝傑偡丅
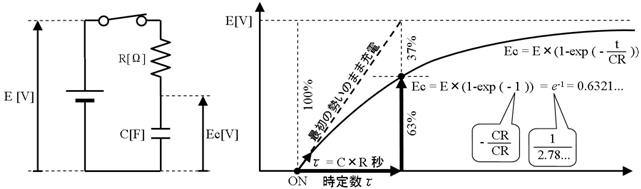
忋壓媡偵側偭偨偨傔偵丄帪掕悢冄屻偺廩揹揹埑偼丄嵟弶偺揹埑偺63%偲側傝傑偡丅乮廩揹偝傟偢偵巆偭偰偄傞揹埑偑37%偱偡乯傑偨丄僐儞僨儞僒偺廩揹揹埑俤們偼丄揹抮偺揹埑傪俤乵倁乶偲偡傞偲丄
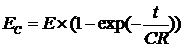
俤倶們倕倢偱偼丄=E1*(1-exp(-T1/C1/R1))偱寁嶼偱偒傑偡丅
丂E1=揹抮偺揹埑乵倁乶丄T1=帪娫乵昩乶丄C1=僐儞僨儞僒偺梕検乵俥乶丄R1=掞峈抣乵兌乶
偱寁嶼偱偒傑偡丅
俆.侾. 楙廗
壓恾偺夞楬偱俽倂傪俷俶偵偟偨屻偺僐儞僨儞僒偺揹埑偺曄壔傪丄侾倣昩枅偵俤倶們倕倢偱寁嶼偟僌儔僼傪昤偄偰偔偩偝偄丅
俆.俀. 摎
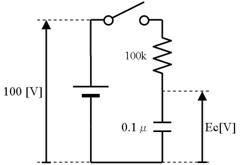
掞峈偑侾侽侽倠兌丄僐儞僨儞僒偑侽丏侾兪丄揹尮偑侾侽侽倁偩偐傜丄俤倶們倕倢偱丄俷俶屻偺帪娫傪帪娫傪俛俀僙儖偵擖傟傟偽丄廩揹揹埑偼=100*(1-(exp(-B2/100E3/0.1E-6))偱寁嶼偱偒傞丅倲偺抣傪師戞偵戝偒偔偟偰丄椺偊偽壓恾偺傛偆偵俤倶們倕倢偵擖椡偟丄寁嶼偝偣傞丅乮壓恾偱偼俠偲俼傕僙儖偐傜梌偊偰偄傞乯
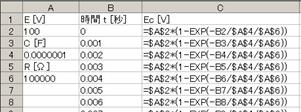
寁嶼寢壥偼師偺傛偆偵側傞丅
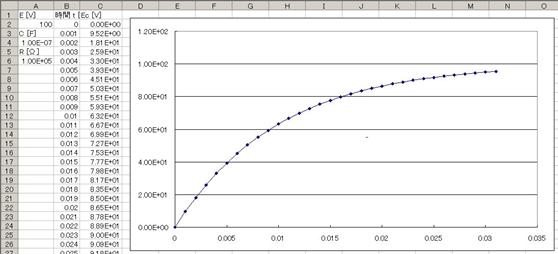
俆.俁. 倕倶倫娭悢傪巊傢側偄夝偒曽乮僔儈儏儗乕僔儑儞乯
杮崁偼梋択偱偡丅嫽枴偑側偗傟偽撉傒旘偽偡偙偲偑偱偒傑偡丅
偙偺栤戣偼壓恾偺僔乕僩傪巊偊偽丄exp娭悢傪巊傢偢偵僔儈儏儗乕僔儑儞偲偄偆曽朄偱傕夝偔偙偲偑偱偒傑偡丅僔儈儏儗乕僔儑儞偱偡偐傜丄擖椡揹埑偺曄壔傕擟堄偵愝掕偱偒傑偡丅
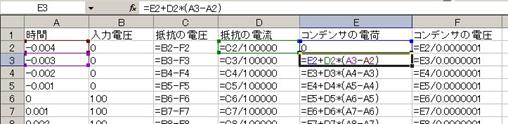
俙楍偵帪娫乮侾倣昩偢偮憹戝乯丄俛楍偵擖椡揹埑乮帺桼側曄壔偑壜擻乯傪擖椡偟丄俤俀僙儖偵僐儞僨儞僒偺揹壸偺弶婜抣乮偙偙偱偼侽僋乕儘儞丗嬻偭傐乯傪擖椡偟傑偡丅
俠楍偺掞峈偺揹埑偼丄擖椡揹埑偲僐儞僨儞僒偺揹埑偺嵎偱偡偐傜丄=B2-F2丄俥楍偺僐儞僨儞僒偺揹埑偼僐儞僨儞僒揹壸乛梕検側偺偱丄=E2/0.1E-6偲幃傪愝掕偟傑偡丅
億僀儞僩偼俤俁僙儖偺僐儞僨儞僒偺揹壸偱偡丅乽僐儞僨儞僒偺揹棳亊帪娫亖僐儞僨儞僒偵棳傟崬傫偩揹壸乿偲偄偆揰偲乽棳傟崬傫偩揹壸偺暘丄僐儞僨儞僒偺揹壸偼憹偊傞乿偲偄偆俀揰傪峫偊偰丄揹棳偺俢俀偵乮侾峴摉偨傝偺乯帪娫乮偙偙偱偼丄俙俁亅俙俀偱侾倣昩偲乯傪妡偗偰僐儞僨儞僒偵棳傟崬傫偩揹壸傪媮傔丄偝傜偵捈慜偺揹壸乮恀忋偺僙儖俤俀乯偵壛偊偰丄=E2+D2*(A3-A2)偲擖椡偟傑偡丅
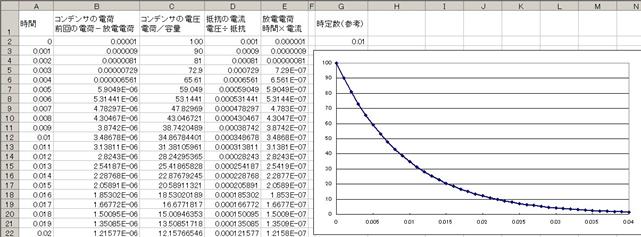
擖椡偟偨抣傗幃傪壓曽岦偵僐僺乕偟偰僔乕僩傪姰惉偟丄寁嶼偟偰僌儔僼傪昤偐偣傞偲丄壓恾偵帵偡偲偍傝丄廩揹偺條巕偑惓偟偔寁嶼偝傟傑偟偨丅
揹埑偺曄壔偵懳偟偰丄侾峴摉偨傝偺帪娫偑廫暘嵶偐偔側偄偲惓偟偔寁嶼偱偒傑偣傫偐傜丄備偭偔傝偲揹埑傗揹棳偑曄壔偡傞掱搙偵丄侾峴摉偨傝偺帪娫乮偙偙偱偼侾倣昩乯傪挷愡偟傑偡丅
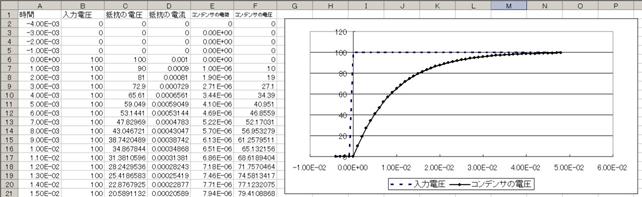
幚偼丄exp娭悢傪巊偆傛傝丄偙偪傜偺曽偑乮巐懃墘嶼偟偐弌偰偒傑偣傫偟丄揹棳丄揹埑丄揹壸偺扨弮側娭學偩偗傪擖椡偡傟偽椙偄偐傜乯暘傝堈偄偺偱偡丅偙偺傛偆側娙扨側寁嶼偐傜丄倕倶倫娭悢偺嬋慄偑弌偰偔傞偺偼丄巹払偺戙傢傝偵丄俤倶們倕倢偑旝暘曽掱幃傪夝偄偰偔傟偰偄傞偐傜偱偡丅乮旝暘曽掱幃偼丄僼儕僐偺峔憿傪尦偵丄僼儕僐偺怳摦傪媮傔傞傛偆側寁嶼偱偡乯偦偺忋偙偺曽朄丄乽搢棫怳巕傪埨掕偝偣傞惂屼傪専摙偡傞乿偲偐丄憡摉偡偛偄帠傑偱偱偒傞傫偱偡丅
俆.係. 楙廗
壓恾偺夞楬偺曻揹偺條巕傪俤倶們倕倢偱僔儈儏儗乕僔儑儞偟丄僐儞僨儞僒偺揹埑傪僌儔僼偱昞帵偟偰偔偩偝偄丅
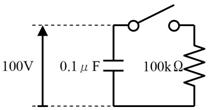
俆.俆. 摎
僐儞僨儞僒偺揹壸偑丄掞峈偵棳傟傞揹棳亊帪娫偢偮尭彮偡傞偙偲傪峫偊偰丄師偺傛偆側僔乕僩傪嶌惉偡傞丅
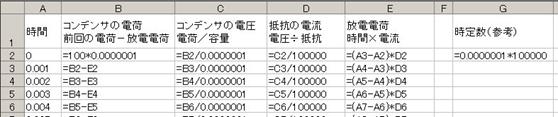
寁嶼偝偣偰僌儔僼傪昤偔偲壓恾偺傛偆偵曻揹偺條巕偑昞帵偝傟傞丅
俇. 僥僽僫儞偺掕棟
壓恾偺夞楬偱俽倂傪俷俶偵偡傞偲丄暘埑偺朄懃偐傜丄僐儞僨儞僒偼俆倁傪栚巜偟偰廩揹偝傟傞偙偲偼暘傝傑偡丅屻偼丄帪掕悢偑寁嶼偱偒傟偽丄廩揹偺條巕傕暘傝傑偡丅
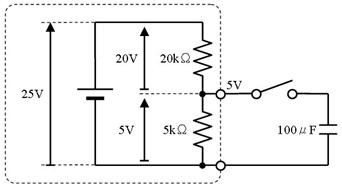
偟偐偟丄忋恾偺傑傑偱偼掞峈偑俀杮偁傝丄帪掕悢偑寁嶼偱偒傑偣傫丅偦偙偱丄忋恾偺揰慄偱埻傫偩晹暘傪丄壓恾偵帵偡僥僽僫儞偺掕棟傪巊偭偰丄堦杮偺掞峈偵抲偒姺偊傑偡丅
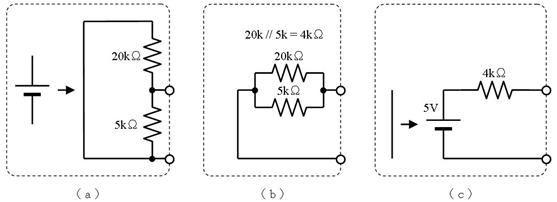
愭偢丄忋恾乮倎乯偵帵偡傛偆偵丄揹抮傪揹慄偵抲偒姺偊傑偡丅偡傞偲丄忋恾乮倐乯偺傛偆偵丄塃懁偐傜尒偨掞峈抣偼丄俀侽倠兌偲俆倠兌偑暲楍偵尒偊傞偺偱丄係倠兌偲側傝傑偡丅嵟屻偵丄忋恾乮們乯偺傛偆偵丄抂巕偵壛傢傞揹埑乮俆倁乯偺揹抮傪愙懕偟捈偟傑偡丅
偙偺傛偆偵丄揹抮偲掞峈傪暋嶨偵慻傒崌傢偣偨夞楬傕丄侾杮偺揹抮偲掞峈偺捈楍夞楬偱昞偡偙偲偑偱偒傑偡丅偙傟偑僥僽僫儞偺掕棟偱偡丅偙偺抲偒姺偊傪峴偆偲丄専摙拞偺夞楬偼壓恾偺傛偆偵側傝傑偡丅
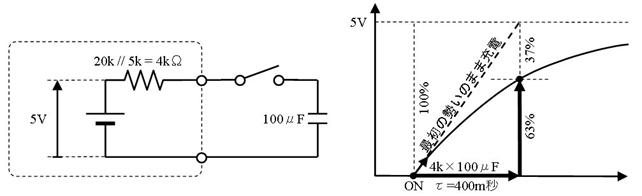
忋恾偺捠傝丄係倠兌傪捠偟偰侾侽侽兪俥傪廩揹偡傞偺偱丄帪掕悢偼係侽侽倣昩偱丄廩揹偺條巕偼忋恾塃懁偺僌儔僼偺傛偆偵側傝傑偡丅
俇.侾. 楙廗
壓恾乮倎乯夞楬傪抂巕偐傜尒偨揹埑偲撪晹掞峈傪丄壓恾乮倐乯偺傛偆偵扨弮偵抲偒姺偊傞偲丄揹埑偲掞峈偼偄偔傜偵側傝傑偡偐丅
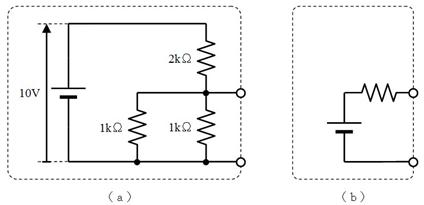
揹埑丂丂丂丂倁丂掞峈抣丂丂丂丂兌
俇.俀. 摎
傑偢丄抂巕偺揹埑傪峫偊傞丅壓恾乮倎乯偺偲偍傝丄壓懁偺暲楍崌惉掞峈偼侾倠兌丄廬偭偰揹抮偺侾侽倁偑侾倠兌偲侾倠兌偱暘埑偝傟偰丄抂巕偵偼俆倁偑弌椡偝傟傞丅
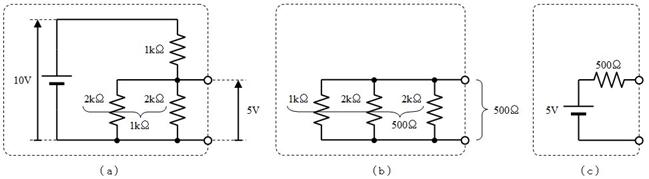
師偵丄揹抮傪揹慄偵抲偒姺偊傞偲丄忋恾乮倐乯偺夞楬偲側傝丅擖椡抂巕偐傜尒偨掞峈抣偼丄俁偮偺掞峈偺暲楍崌惉掞峈偱丄俆侽侽兌偲側傞丅
揹埑丂丂丂俆倁丂掞峈抣丂俆侽侽兌
俈. 廳偹崌傢偣偺尨棟
廳偹崌傢偣偺尨棟偼丄揹抮偑暋悢偁傞夞楬偺揹棳傪娙扨偵媮傔傞曽朄偱偡丅乽暋悢偺揹抮偑摥偄偰偄傞夞楬偵棳傟傞揹棳偼丄偦傟偧傟偺揹抮偑侾偮偩偗摥偄偰棳傟偨揹棳傪崌寁偡傟偽寁嶼偱偒傞乿偲偄偆峫偊曽偱偡丅揹埑偲揹棳偑斾椺偡傞乮偮傑傝丄僆乕儉懃偑捠梡偡傞乯夞楬偱偁傟偽偄偮偱傕棙梡偱偒傑偡丅
嬶懱揑偵偼傑偢丄暋悢偺揹抮偺偳傟偐侾偮偩偗偵拲栚偟丄偦傟埲奜偺揹抮偼乽摫慄乿偲峫偊偰丄奺晹偺揹棳傪媮傔傑偡丅師偵丄暿偺揹抮偵拲栚偟丄偦傟埲奜偺揹抮偼乽摫慄乿偲峫偊偰丄奺晹偺揹棳傪媮傔傑偡丅偙偺傛偆偵慡偰偺揹抮偵弴偵拲栚偟偰揹棳傪媮傔傑偡丅嵟屻偵丄偙傟傑偱偵媮傔偨揹棳傪崌寁偡傟偽丄慡偰偺揹抮偑妶摦偟偨偲偒偺揹棳偑暘傝傑偡丅
壓恾偺椺偱偼俇倁偲侾俀倁偺俀偮偺揹抮偑摥偄偰偄傑偡丅偙偙偱偼丄俼侾丄俼俀丄俼俁偵棳傟傞揹棳傪廳偹崌傢偣偺尨棟偱媮傔傑偡丅
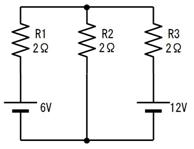
奺晹偺揹棳偼丄壓恾乮倎乯乮倐乯乮們乯偵帵偡俁抜奒偱峫偊傑偡丅傑偢乮倎乯偱偼俇倁偺揹抮偵拲栚偟偰丄偦傟埲奜偺乮侾俀倁偺乯揹抮偼摫慄偱偁傞偲峫偊丄奺晹偺揹棳傪媮傔傑偡丅師偵乮倐乯偱偼侾俀倁偺揹抮偵拲栚偟偰丄偦傟埲奜偺乮俇倁偺乯揹抮偼摫慄偱偁傞偲峫偊丄奺晹偺揹棳傪媮傔傑偡丅嵟屻偵乮們乯偱丄乮倎乯偱媮傔偨揹棳偲乮倐乯偱媮傔偨揹棳傪崌寁偡傟偽丄揹抮偑俀偮偲傕妶摦偟偰偄傞偲偒偺奺晹偺揹棳偑寁嶼偱偒傑偡丅
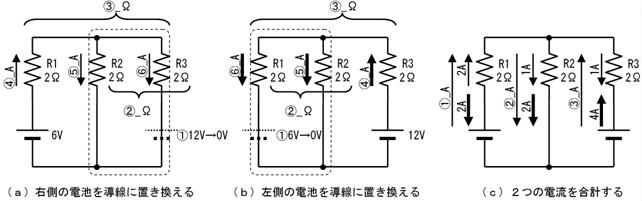
俈.侾. 楙廗
忋恾傪尒側偑傜壓昞偵婰擖偟偰丄揹棳傪媮傔傑偡丅
|
斣崋
|
栤戣
|
摎
|
|
乮倎乯
|
嘆侾俀倁偺揹抮傪摫慄偲峫偊傑偡
|
亅
|
|
嘇
|
俼俀偲俼俁偺暲楍崌惉掞峈抣偼丄
|
丂兌
|
|
嘊
|
揹抮偐傜尒偨夞楬慡懱偺掞峈抣偼丄
|
丂兌
|
|
嘋
|
俼侾偵棳傟傞揹棳偼丄
|
丂俙
|
|
嘍
|
俼俀偲俼俁偵棳傟傞揹棳偼丄乮暘棳偱乧乯
|
丂俙
|
|
乮倐乯
|
嘆俇倁偺揹抮傪摫慄偲峫偊傑偡
|
亅
|
|
嘇
|
俼侾偲俼俀偺暲楍崌惉掞峈抣偼丄
|
丂兌
|
|
嘊
|
揹抮偐傜尒偨夞楬慡懱偺掞峈抣偼丄
|
丂兌
|
|
嘋
|
俼俁偵棳傟傞揹棳偼丄
|
丂俙
|
|
嘍
|
俼俀偲俼俁偵棳傟傞揹棳偼丄乮暘棳偱乧乯
|
丂俙
|
|
乮們乯
|
乮倎乯偲乮倐乯偱媮傔偨揹棳傪崌寁偟傑偡
|
亅
|
|
嘆
|
俼侾偵棳傟傞揹棳偼丄
|
丂俙
|
|
嘇
|
俼俀偵棳傟傞揹棳偼丄
|
忋岦偒丒壓岦偒
丂俙
|
|
嘊
|
俼俁偵棳傟傞揹棳偼丄
|
忋岦偒丒壓岦偒
丂俙
|
俈.俀. 摎
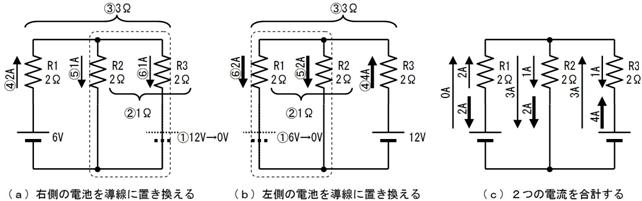
|
斣崋
|
栤戣
|
摎
|
|
乮倎乯
|
嘆侾俀倁偺揹抮傪摫慄偲峫偊傑偡
|
亅
|
|
嘇
|
俼俀偲俼俁偺暲楍崌惉掞峈抣偼丄
|
侾兌
|
|
嘊
|
揹抮偐傜尒偨夞楬慡懱偺掞峈抣偼丄
|
俁兌
|
|
嘋
|
俼侾偵棳傟傞揹棳偼丄
|
俀俙
|
|
嘍
|
俼俀偲俼俁偵棳傟傞揹棳偼丄乮暘棳偱乧乯
|
侾俙
|
|
乮倐乯
|
嘆俇倁偺揹抮傪摫慄偲峫偊傑偡
|
亅
|
|
嘇
|
俼侾偲俼俀偺暲楍崌惉掞峈抣偼丄
|
侾兌
|
|
嘊
|
揹抮偐傜尒偨夞楬慡懱偺掞峈抣偼丄
|
俁兌
|
|
嘋
|
俼俁偵棳傟傞揹棳偼丄
|
係俙
|
|
嘍
|
俼俀偲俼俁偵棳傟傞揹棳偼丄乮暘棳偱乧乯
|
俀俙
|
|
乮們乯
|
乮倎乯偲乮倐乯偱媮傔偨揹棳傪崌寁偟傑偡
|
亅
|
|
嘆
|
俼侾偵棳傟傞揹棳偼丄乮俀俙亅俀俙乯
|
侽俙
|
|
嘇
|
俼俀偵棳傟傞揹棳偼丄乮俀俙亄侾俙乯
|
忋岦偒丒壓岦偒
俁俙
|
|
嘊
|
俼俁偵棳傟傞揹棳偼丄乮係俙亅侾俙乯
|
忋岦偒丒壓岦偒
俁俙
|
俉. 僐僀儖
僐僀儖偼僐儞僨儞僒偵斾傋傞偲暘偐傝擄偔姶偠傞晹昳偱偡偑丄壓恾偺傛偆偵乽揹棳偱夞傞偼偢傒幵乿偲峫偊傞偲摦嶌傪僀儊乕僕偱偒傑偡丅
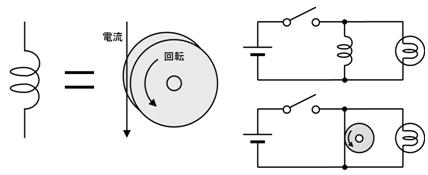
忋恾塃懁偺夞楬偱僐僀儖偺摥偒傪愢柧偟傑偡丅壓恾嵍懁偺傛偆偵丄僗僀僢僠傪俷俶偵偡傞偲丄僐僀儖偵揹埑偑壛傢傝丄偼偢傒幵偼備偭偔傝偲夞揮傪巒傔傑偡丅偮傑傝丄揹棳偼備偭偔傝偲憹偊偰備偒傑偡丅
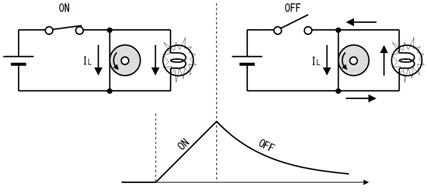
揹棳偑憹偊偨偲偙傠偱丄忋恾塃懁偺傛偆偵僗僀僢僠傪俷俥俥偵偡傞偲丄偼偢傒幵偼惃偄偑晅偄偰偄傞偨傔丄俷俥俥屻傕夞揮傪懕偗丄忋恾塃懁偺宱楬偱揹棳偑棳傟偰丄揹媴偑岝傝懕偗傑偡丅
揹媴偵僄僱儖僊傪嫙媼偟偰偄傞偨傔丄偼偢傒幵偼師戞偵夞揮偑抶偔側傝丄夞揮偺僄僱儖僊傪偡傋偰揹媴偵憲傝崬傓偲掆巭偟傑偡丅
僐僀儖偺戝偒偝乮僀儞僟僋僞儞僗乯偼丄偼偢傒幵偺廳偝偵懳墳偟偰偄傑偡丅偱偡偐傜戝偒側僐僀儖偼揹埑傪妡偗偰傕側偐側偐揹棳偑憹壛偣偢丄彫偝側僐僀儖偼偡偖偵揹棳偑憹壛偟傑偡丅偱偡偐傜丄僐僀儖偺戝偒偝偼師偺傛偆偵寁嶼偟傑偡丅
俇倁偺揹埑傪壛偊偰丄揹棳偑俁俙偵憹偊傞傑偱偵丄俀昩妡偐傟偽丄
僐僀儖偺戝偒偝
亖 俇倁
亊 俀昩
亐 俁俙
亖 係俫
俤倶們倕倢偱偼丄=E1*T1/I1
偱偡偐傜僐僀儖偵棳傟傞揹棳偼丄
僐僀儖偺揹棳
亖 揹埑
亊 帪娫
亐 僐僀儖偺戝偒偝
俤倶們倕倢偱偼丄=E1*T1/L1
偲偙傠偱丄揝傗僼僃儔僀僩側偳偺帴惈懱偺恈乮僐傾乯偵慄傪姫偔偲丄僐僀儖傪彫宍偵偱偒傑偡丅偨偩偟丄帴惈懱偵偼乽偙傟埲忋嫮偄帴愇偵偼惉傟側偄乿偲偄偆尷搙偑偁傞偺偱丄戝偒側揹棳傪棳偡偲丄偦偺尷搙偵払偟偰乽帴婥朞榓乿偲偄偆尰徾偑婲偙傝傑偡丅
壓恾偵帵偡捠傝丄僐傾偑帴婥朞榓偡傞偲乽揹棳偑偦傟埲忋憹偊側偄乿偺偱偼側偔丄乽揹棳偑媫寖偵憹壛偡傞乿偡傞偺偱拲堄偑昁梫偱偡丅
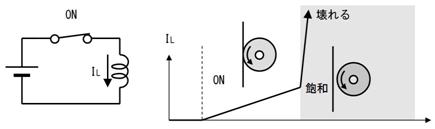
偮傑傝丄忋恾塃懁偺僌儔僼忋偵帵偡傛偆偵丄偼偢傒幵偑偁傑傝偵寖偟偔夞揮偡傞偲揹慄偐傜棧傟偰偟傑偄乮僐僀儖偑丄揹慄偵曄恎偟偰乯揹棳偑棳傟曻戣偵側傞偲偄偆僀儊乕僕偱偡丅
俉.侾. 楙廗
嘆俆倁傪壛偊傞偲侾兪昩偱侾侽倣俙偵揹棳偑憹壛偟傑偟偨丅偙偺僐僀儖偺戝偒偝偼偄偔傜偱偡偐丠
嘇俆侽倣俫偺僐僀儖偵侾俆倁偺揹埑傪侾倣昩壛偊傑偟偨丅揹棳偼壗俙偵憹壛偟傑偡偐丅
俉.俀. 摎
嘆僐僀儖偺戝偒偝 亖
俆倁 亐 侾侽倣俙 亐 侾兪昩
亖 俆侽侽兪俫丂=5*1E-6/10E-3
嘇僐僀儖偺揹棳 亖 侾俆倁 亊
侾倣昩 亐 俆侽倣俫 亖 俁侽侽倣俙
=15*1E-3/50E-3
俋. 僼儔僀僶僢僋
壓恾乮倎乯偺夞楬偱僗僀僢僠傪俷俶偵偡傞偲丄僐僀儖偺忋懁偵亄偺揹埑偑壛傢傝傑偡丅偙偺偨傔丄摨恾乮倐乯偺傛偆偵偼偢傒幵偺夞揮偑師戞偵懍偔側傝丄壓恾塃偺僌儔僼偵奃怓慄偱帵偡傛偆偵揹棳偑憹壛偟偰峴偒傑偡丅
偙偙偱椺偊偽揹棳偑侾俙偵憹壛偟偨偲偒偵僗僀僢僠傪俷俥俥偵偡傞偲丄偡偱偵偼偢傒幵偼惃偄椙偔夞偭偰偍傝丄僐僀儖偼僗僀僢僠偑俷俥俥偱偁傞偵傕偐偐傢傜偢侾俙偺揹棳傪棳偟懕偗傛偆偲偟傑偡丅偙偺偨傔僐僀儖偺壓懁偵崅偄亄偺揹埑偑敪惗偟丄棧傟偨愙揰傪壩壴偲側偭偰揹棳偑棳傟傑偡丅愙揰偵壩壴偑敪惗偡傞偲乮壩壴偼崅偄僄僱儖僊乕傪徚旓偡傞偺偱乯偼偢傒幵偺夞揮偼抁帪娫偱掆巭偟丄揹棳偼巭傑傝傑偡丅
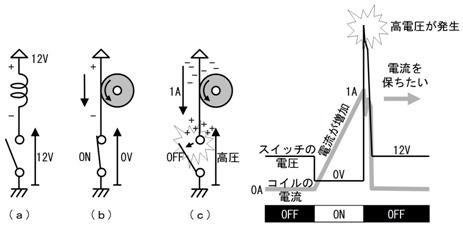
偙偺傛偆偵僐僀儖偵棳傟傞揹棳傪撍慠巭傔偨偲偒丄崅偄揹埑偑敪惗偡傞尰徾傪乽僼儔僀僶僢僋乿偲屇傃丄敪惗偡傞崅偄揹埑傪乽僼儔僀僶僢僋揹埑乿丄柍棟偵僗僀僢僠傪棳傟傞揹棳傪乽僼儔僀僶僢僋揹棳乿偲屇傃傑偡丅
僼儔僀僶僢僋偵傛偭偰丄愙揰偑壩壴偱彎傒傑偡偟丄敿摫懱偱偁傟偽攋懝偟傑偡丅偙偺偨傔壓恾偵帵偡傛偆側丄俷俥俥帪偺揹棳傪媧廂偡傞夞楬乮僗僫僶夞楬乯傪暿偵愝偗丄壩壴偺敪惗傪巭傔傑偡丅
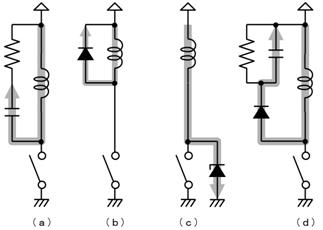
僗僫僶夞楬偺摥偒偵偮偄偰偼丄暿搑愢柧偟傑偡丅
侾侽. 撪晹掞峈侾
壓恾乮倎乯偺傛偆偵丄係倁偲彂偐傟偨揹抮偺揹埑傪應掕偡傞偲丄妋偐偵係倁偱偟偨丅偦偙偱丄壓恾乮倐乯偺傛偆偵丄侾俙棳傟傞帠傪婜懸偟偰丄係兌偺掞峈乮偙偺傛偆偵揹棳傪棳偡偨傔偺掞峈傪乽晧壸掞峈乿偲屇傃傑偡乯傪愙懕偡傞偲丄側偤偐侽丏俉俙偟偐棳傟傑偣傫偱偟偨丅
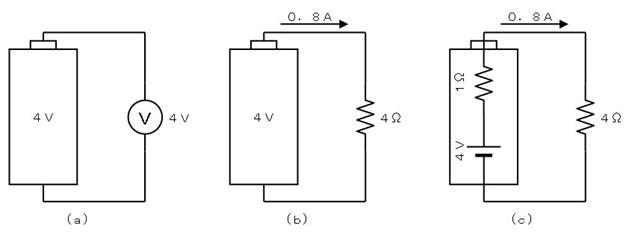
偙偺棟桼偼丄忋恾乮們乯偵帵偡傛偆偵丄揹抮偺撪晹偵乮塀偝傟偨乯掞峈偑偁傝丄偦偺寢壥丄崌寁偺掞峈抣偑俆兌偲側傝丄揹棳偑尭彮偟偨偨傔偱偡丅
偙偺傛偆側丄乽乮昁梫側偄偺偵乯慺巕偵擖偭偰偄傞掞峈乿傪乽撪晹掞峈乿偲屇傃傑偡丅戝偒側揹棳傪棳偡夞楬偱偼丄撪晹掞峈傪峫偊偰愝寁偟側偄偲丄揹棳偑巚偭偨傛傝彫偝偔側偭偰偟傑偄傑偡丅
傕偪傠傫揹抮儊乕僇乕偼堄抧埆偱撪晹掞峈傪擖傟偰偄傞栿偱偼偁傝傑偣傫丄揹抮儊乕僇乕偼撪晹掞峈傪柍偔偦偆偲搘椡偟偰偄傞偺偱偡偑丄峔憿忋巭傓傪摼偢擖偭偰偟傑偆栿偱偡丅
侾侽.侾. 楙廗
壓恾偺傛偆偵丄撪晹掞峈侾兌丄婲揹椡係倁偺揹抮傪俀杮捈楍偵愙懕偟丄侾俙偺揹棳傪庢傝弌偡偨傔偵偼丄晧壸掞峈偼壗兌偵偡傋偒偱偡偐丅
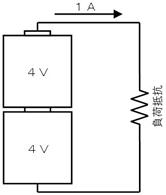
晧壸掞峈丗丂丂丂兌
侾侽.俀. 摎
撪晹掞峈傪峫偊傞偲丄夞楬偼壓恾嵍偺傛偆偵丄奺侾兌偺撪晹掞峈偑偁傝傑偡丅傑偨丄婲揹椡乮揹抮偺揹埑乯偺崌寁偼俉倁偱偡丅偱偡偐傜丄侾俙棳偡偨傔偵偼丄夞楬慡懱偺掞峈抣傪俉兌偵偡傞昁梫偑偁傝傑偡丅偙偺偨傔丄俇兌偺晧壸掞峈傪愙懕偡傟偽丄夞楬偵侾俙傪棳偡偙偲偑弌棃傑偡丅
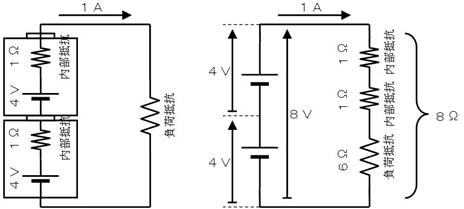
晧壸掞峈丗丂俇丂兌
侾侾. 撪晹掞峈俀
壓恾乮倎乯偺傛偆偵丄俁倁偺揹尮傪侾侽倠偲俀侽倠偱暘埑偡傞偲丄俀侽倠偺椉抂偵偼俀倁偑惗偠傞敜偱偡丅偦偙偱丄摨恾乮倐乯偺傛偆偵俀侽倠偺椉抂揹埑傪應掕偡傞偲丄側偤偐侾丏俆倁偟偐偁傝傑偣傫偱偟偨丅
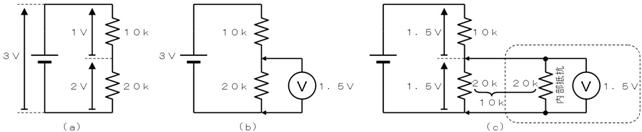
偙偺尰徾傕乽撪晹掞峈乿偑尨場偱偡丅忋恾乮們乯偵帵偡傛偆偵丄杮棃偼揹棳傪棳偝側偄敜偺揹埑寁偵傕丄乽撪晹掞峈乿乮偙偙偱偼俀侽倠乯偑偁傝傑偡丅
偙偺偨傔丄夞楬偵揹埑寁傪愙懕偟偨偙偲偱丄壓懁偺俀侽倠兌偲揹埑寁偺撪晹掞峈偺俀侽倠兌偑暲楍愙懕偝傟丄椉幰偑崌傢偝偭偰侾侽倠偲偟偰嶌梡偟傑偡丅寢壥偲偟偰丄忋懁偺侾侽倠偲壓懁偺侾侽倠偱暘埑偝傟偨偙偲偵側傝丄壓懁偺俀侽倠兌偺椉抂偵偼丄揹尮偺俁倁偺敿暘丄偮傑傝侾丏俆倁偑惗偠偨偺偱偡丅
傕偪傠傫寁婍儊乕僇乕偼堄抧埆偱撪晹掞峈傪擖傟偰偄傞栿偱偼偁傝傑偣傫丄儊乕僇乕偼撪晹掞峈傪柍偔偦偆偲搘椡偟偰偄傞偺偱偡偑丄峔憿忋巭傓傪摼偢擖偭偰偟傑偆栿偱偡丅崱擔偱偼乮捠忢偺梡搑偱偁傟偽乯慡偔揹棳偑棳傟側偄偲峫偊偰椙偄揹埑寁傕憹偊偰偄傑偡丅乮撪晹掞峈偑侾俿兌埲忋偁傝傑偡乯
侾侾.侾. 楙廗
壓恾偺傛偆偵丄侾侽侽倁偺揹尮偐傜丄侾侽俵兌傪宱桼偟偰揹埑傪應掕偡傞偲丄揹埑寁偼俆侽倁傪帵偟傑偟偨丅偙偺揹埑寁偺撪晹掞峈傪摎偊偰偔偩偝偄丅
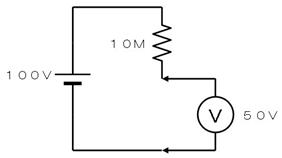
撪晹掞峈丂丂丂丂丂兌
侾侾.俀. 摎
侾侽侽倁偑俆侽倁乮敿暘乯偵暘埑偝傟偰偄傞偺偱丄忋懁偺掞峈偲壓懁偺掞峈乮撪晹掞峈乯偼摨偠偱偡丅偙偺偨傔撪晹掞峈偼侾侽俵兌偱偡丅
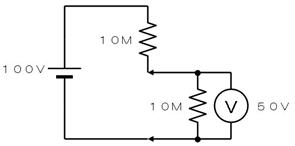
撪晹掞峈丂侾侽俵丂兌
侾俀. 僄僱儖僊偲巇帠
偙偙偐傜愢柧偡傞乽巇帠乿傗乽巇帠棪乿偼丄揹婥偺悽奅偲丄尰幚偺悽奅乮壏搙傗塣摦側偳偺恎嬤側帠暱乯傪娭楢晅偗傞忋偱栶棫偪傑偡丅偨偲偊偽乽偙偺婡夿偵偼壗倂偔傜偄偺儌乕僞偑昁梫偐丠乿側偳傪丄偞偭偔傝寁嶼偱偒傞傛偆偵側傝傑偡丅偱偡偐傜丄僄僱儖僊傗巇帠偵偮偄偰偼丄楙廗傕傑偠偊偰偪傚偭偲徻偟偔愢柧偟傑偡丅
彯丄杮彂偱偼暘傝堈偔偡傞偨傔乽巇帠乿偵娭楢偡傞乽椙偔帡偨乿扨埵傗峫偊曽傪乽慡偔摨偠傕偺乿偲偟偰埖偄傑偡丅偦偺傎偆偑娙扨偱丄幚梡忋壗偺栤戣傕柍偄偐傜偱偡丅
壓恾嵍懁偺傛偆偵丄侾侽俀倗偺傝傫偛傪侾倣帩偪忋偘傞乽巇帠乿偑侾俶倣乮僯儏乕僩儞儊乕僩儖乯偱偡丅俶倣偺戙傢傝偵丄俰乮僕儏乕儖乯傗丄倂昩乮儚僢僩昩乯傪巊偆帠傕偱偒傑偡丅傑偨丄乽巇帠乿偼乽僄僱儖僊乿偲傕屇傃傑偡丅
帩偪忋偘傞偺偱偼側偔丄壓恾塃忋偵帵偡偲偍傝丄壸暔傪侾侽俀倗乮侾俶乯偺 椡 偱丄侾倣墶偵堷偒悹傞巇帠傕侾俶倣偱偡丅
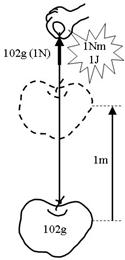 丂丂丂
丂丂丂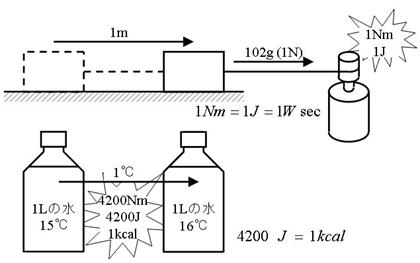
傑偨丄忋恾壓晹偵帵偡偲偍傝丄係俀侽侽俶倣偺僄僱儖僊偑偁傟偽侾儕僢僩儖偺悈傪侾亷壏傔傞偙偲偑偱偒傑偡丅
侾俀.侾. 楙廗
壓昞偺巇帠傪媮傔偰摎棑偵丄奺庬偺扨埵偱婰擖偟偰偔偩偝偄丅
|
斣崋
|
栤戣
|
摎
|
|
嘆
|
俁侽俇倗偺壸暔傪係倣帩偪忋偘傞巇帠偼
|
俶倣
俰
倂昩
|
|
嘇
|
俀俴偺悈傪俆亷抔傔傞巇帠偼
|
俶倣
俰
倂昩
|
侾俀.俀. 摎
|
斣崋
|
栤戣
|
摎
|
|
嘆
|
俁侽俇倗偺壸暔傪係倣帩偪忋偘傞巇帠偼
俁侽俇倗亐侾侽俀倗亖俁俶
俁俶亊係倣亖侾俀俶倣
|
侾俀俶倣
侾俀俰
侾俀倂昩
|
|
嘇
|
俀俴偺悈傪俆亷抔傔傞巇帠偼
係俀侽侽俰亊俀俴亊俆亷亖係俀侽侽侽俰
|
係俀侽侽侽俶倣
係俀侽侽侽俰
係俀侽侽侽倂昩
|
侾俁. 揹椡乮巇帠棪乯
巇帠棪偼乽侾昩娫偵偱偒傞巇帠偺検乿偱丄扨埵偼俶倣乛昩偱偡丅乽侾昩偵偱偒傞乿偲偄偆偲偙傠偑丄乽巇帠乿偲偺堘偄偱偡丅乮俶倣乛昩偺戙傢傝偵丄俰乛昩傗丄倂傪巊偆帠傕偱偒傑偡乯
壓恾偵帵偡偲偍傝丄壸暔傪侾侽俀倗乮侾俶乯偺 椡
偱堷偭挘傝丄侾昩娫偁偨傝丄侾倣偢偮堷偒偢傞偙偲偑偱偒傟偽丄巇帠棪偼侾俶倣乛昩乮僯儏乕僩儞儊乕僩儖枅昩乯偱偡丅侾昩娫偵侾俶倣偺巇帠偑偱偒傑偡偐傜丅侾侽昩娫懸偰偽丄侾侽俶倣偺巇帠偑偱偒傑偡丅
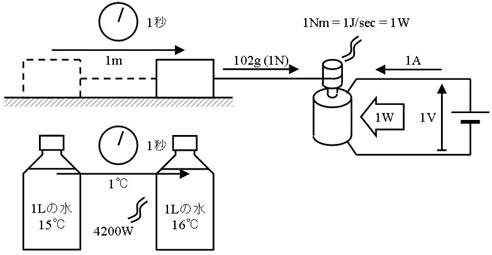
傑偨丄忋恾塃懁偵偁傞傛偆偵丄揹埑侾倁偱侾俙偺揹棳偑棳傟偰偄傞偲偒乽侾倂乮儚僢僩乯偺揹椡偑徚旓偝傟偰偄傞乿偲尵偄傑偡丅
揹椡倂偲巇帠棪俶倣乛昩乮俰乛昩乯偼摨偠傕偺偱丄侾倂偺揹椡傪柍懯側偔巊偊偽丄侾昩娫偵侾俶倣偺巇帠偑偱偒傑偡丅
揹椡偼揹埑偲揹棳傪妡偗偰丄師偺傛偆偵寁嶼偟偰媮傔傑偡丅
揹椡丂亖丂揹埑丂亊丂揹棳
丂椺偊偽丂俀侽倁丂亊丂俆俙丂亖丂侾侽侽倂
僆乕儉懃偵傛傟偽丄揹埑偼揹棳亊掞峈丄揹棳偼揹埑亐掞峈偱偡偐傜丄揹椡偼師偺寁嶼偱傕媮傔傞偙偲偑偱偒傑偡丅
揹椡丂亖丂揹棳俀丂亊丂掞峈丂丂丂丂乮揹棳俀偼揹棳亊揹棳偺帠偱偡乯
丂椺偊偽丂俆俙俀丂亊丂係兌丂亖丂侾侽侽倂
揹椡丂亖丂揹埑俀丂亐丂掞峈
丂椺偊偽丂俀侽倁俀丂亐丂係兌丂亖丂侾侽侽倂
侾侽侽倂偺巇帠棪偼丄懠偺扨埵傪巊偭偰昞偡偙偲傕偱偒傑偡丅
侾侽侽倂丂亖丂侾侽侽俰乛昩丂亖丂侾侽侽俶倣乛昩
乮侾侽俀倗偺傝傫偛傪丄堦昩偱侾侽侽倣帩偪忋偘傑偡乯
偙偺傛偆偵巇帠傗巇帠棪偱偼丄暋悢偺扨埵偑丄傎傏摨偠堄枴偱巊傢傟傑偡丅偦傟傜偺扨埵傪壓昞偵帵偟傑偡丅
|
庬椶
|
扨埵
|
屇傃柤
|
堄枴
|
|
巇帠
|
俶倣
|
僯儏乕僩儞儊乕僩儖
|
侾俶乮侾侽俀倗乯偺椡偱侾倣堷偭挘傞巇帠
|
|
俰
|
僕儏乕儖
|
|
倂昩
|
儚僢僩僙僇儞僪
|
侾倁偱侾俙偺揹棳傪侾昩娫棳偡巇帠
|
|
擬検
|
倠們倎倢
|
僉儘僇儘儕乕
|
侾倠倗偺悈傪侾亷壏傔傞偺偵昁梫側擬検
係俀侽侽俰亖侾倠們倎倢
|
|
巇帠棪
|
俶倣乛昩
|
僯儏乕僩儞儊乕僩儖枅昩
|
侾俶乮侾侽俀倗乯偺椡偱
侾昩偁偨傝侾倣堷偭挘傞巇帠棪
|
|
俰乛昩
|
僕儏乕儖枅昩
|
|
倂
|
儚僢僩
|
侾倁偱侾俙偺揹棳傪棳偡巇帠棪
|
侾俁.侾. 楙廗
壓昞偺巇帠傪媮傔偰摎棑偵丄奺庬偺扨埵偱婰擖偟偰偔偩偝偄丅扐偟丄僄僱儖僊偼栚揑偺偨傔偵柍懯側偔棙梡偝傟傞偲峫偊偰偔偩偝偄丅
|
斣崋
|
栤戣
|
摎
|
|
嘆
|
係昩娫偵俆侾侽倗偺壸暔傪俀侽倣帩偪忋偘傞巇帠棪偼
|
俶倣乛昩
俰乛昩
倂
|
|
嘇
|
侾侽暘偱俁俴偺悈傪俆亷抔傔傞巇帠棪偼
|
俶倣乛昩
俰乛昩
倂
|
|
嘋
|
俁侽倁俀俙偺儌乕僞偺巇帠棪偼
|
俶倣乛昩
俰乛昩
倂
|
|
嘋
|
俁侽倁俀俙偺儌乕僞偑丄俀侽昩娫摦嶌偟偰峴偆巇帠偼
|
俶倣
俰
倂昩
|
侾俁.俀. 摎
|
斣崋
|
栤戣
|
摎
|
|
嘆
|
係昩娫偵俆侾侽倗偺壸暔傪俀侽倣帩偪忋偘傞巇帠棪偼
俆侾侽亐侾侽俀亖俆俶
俆俶亊俀侽倣亐係昩亖俀俆
|
俀俆俶倣乛昩
俀俆俰乛昩
俀俆倂
|
|
嘇
|
侾侽暘偱俁俴偺悈傪俆亷抔傔傞巇帠棪偼
俁俴亊俆亷亊係俀侽侽亖俇俁侽侽侽俰
俇俁侽侽侽俰亐俇侽侽昩亖侾侽俆俰乛昩
|
侾侽俆俶倣乛昩
侾侽俆俰乛昩
侾侽俆倂
|
|
嘋
|
俁侽倁俀俙偺儌乕僞偺巇帠棪偼
俁侽倁亊俀俙亖俇侽倂
|
俇侽俶倣乛昩
俇侽俰乛昩
俇侽倂
|
|
嘋
|
俁侽倁俀俙偺儌乕僞偑丄俀侽昩娫摦嶌偟偰峴偆巇帠偼
俁侽倁亊俀俙亖俇侽倂
俇侽倂亊俀侽昩亖侾俀侽倂昩
|
侾俀侽俶倣
侾俀侽俰
侾俀侽倂昩
|
侾俁.俁. 楙廗
壓恾偺夞楬偺嘆乣嘋偺揹埑傗揹椡傪媮傔偰偔偩偝偄丅
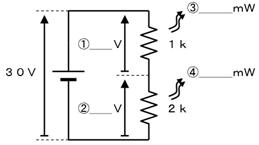
侾俁.係. 摎
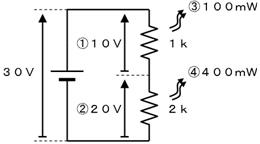
嘆嘇暘埑偺朄懃偵傛傝丄嘆偼侾侽倁丄嘇偼俀侽倁
嘊侾侽倁亊侾侽倁亐侾倠兌偱丄侾侽侽倣倂
嘋俀侽倁亊俀侽倁亐侾倠兌偱丄係侽侽倣倂
侾俁.俆. 楙廗
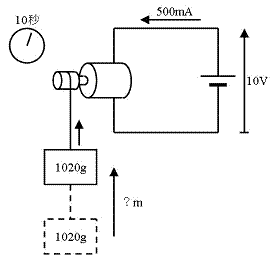
壓恾偺傛偆偵丄侾侽倁俆侽侽倣俙偱儌乕僞傪嬱摦偟偰侾丏侽俀倠倗偺壸暔傪帩偪忋偘傑偡丅偙偺儌乕僞傪侾侽昩娫摦嶌偝偣傟偽丄壗儊乕僩儖帩偪忋偘傞偙偲偑偱偒傑偡偐丅壓昞塃懁偺楍偵彂偒崬傫偱摎偊偰偔偩偝偄丅扐偟丄儌乕僞偵壛偊偨揹椡偼柍懯側偔壸暔偺帩偪忋偘傞帠偵巊傢傟傞偲偟傑偡丅
|
斣崋
|
崁栚
|
摎
|
|
嘆
|
儌乕僞偺徚旓揹椡
|
倂
|
|
嘇
|
儌乕僞偺侾侽昩娫偺巇帠
|
俶倣
|
|
嘊
|
壸暔傪堷偔椡
|
俶
|
|
嘋
|
壸暔傪堷偔嫍棧
|
倣
|
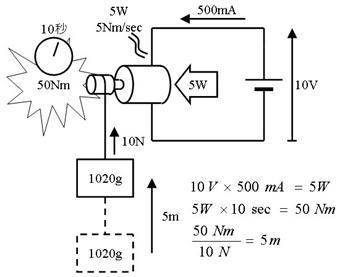
侾俁.俇. 摎
|
斣崋
|
崁栚
|
摎
|
愢柧
|
|
嘆
|
儌乕僞偺徚旓揹椡
|
俆倂
|
侾侽倁亊俆侽侽倣俙
|
|
嘇
|
儌乕僞偺侾侽昩娫偺巇帠
|
俆侽俶倣
|
俆倂亊侾侽昩
乮俆俶倣乛昩亊侾侽昩乯
|
|
嘊
|
壸暔傪堷偔椡
|
侾侽俶
|
侾侽俀侽倗乛侾侽俀亖侾侽俶
乮侾俶亖侾侽俀倗倵乯
|
|
嘋
|
壸暔傪帩偪忋偘傞嫍棧
|
俆倣
|
俆侽俶倣乛侾侽俶
|
幚嵺偵偼條乆側偲偙傠偱僄僱儖僊偑乮儌乕僞偑敪擬偡傞摍偱乯柍懯偵側傝丄帩偪忋偘傞崅偝偼彫偝偔側傝傑偡丅
侾俁.俈. 楙廗
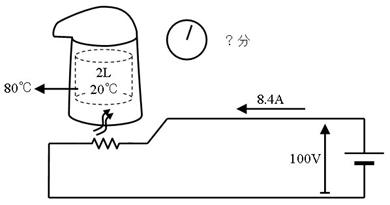
壓恾偺傛偆偵丄侾侽侽倁丄俉丏係俙偺僸乕僞傪巊偭偰丄揹婥億僢僩偵擖偭偨俀侽亷偺悈俀儕僢僩儖傪丄俉侽亷傑偱壏傔傞偵偼丄壗暘昁梫偱偡偐丅扐偟丄擬偼奜偵摝偘側偄傕偺偲偟傑偡丅
|
斣崋
|
崁栚
|
摎
|
|
嘆
|
抔傔偰忋徃偝偣傞壏搙
|
亷
|
|
嘇
|
抔傔傞偺偵昁梫側僄僱儖僊乕
|
俰
|
|
嘊
|
僸乕僞偺揹椡
|
倂
|
|
嘋
|
抔傔傞帪娫乮昩乯
|
昩
|
|
嘍
|
抔傔傞帪娫乮暘乯
|
暘
|
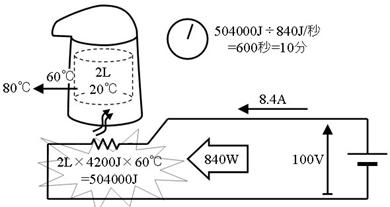
侾俁.俉. 摎
|
斣崋
|
崁栚
|
摎
|
愢柧
|
|
嘆
|
抔傔偰忋徃偝偣傞壏搙
|
俇侽亷
|
俉侽亷亅俀侽亷
|
|
嘇
|
抔傔傞偺偵昁梫側僄僱儖僊乕
|
俆侽係侽侽侽俰
|
俀俴亊俇侽亷亊係俀侽侽俰
|
|
嘊
|
僸乕僞偺揹椡
|
俉係侽倂
|
侾侽侽倁亊俉丏係俙
|
|
嘋
|
抔傔傞帪娫乮昩乯
|
俇侽侽昩
|
俆侽係侽侽侽亐俉係侽
|
|
嘍
|
抔傔傞帪娫乮暘乯
|
侾侽暘
|
俇侽侽昩亐俇侽
|
侾係. 揹椡検
揹椡検偼丄揹椡乮巇帠棪乯偵帪娫傪妡偗偰丄巊梡偟偨揹婥僄僱儖僊乮巇帠乯偺検傪媮傔偨傕偺偱偡丅偱偡偐傜揹椡検偼丄婎杮揑偵偼俰乮僕儏乕儖乯傗倂昩乮儚僢僩僙僐儞僪乯偲摨偠僞僀僾乮巇帠乯偺扨埵偱偡丅
俰傗倂昩偲偺堘偄偼丄帪娫偵乽昩乿偱偼側偔乽帪娫乿乮傾儚乕丗倛乯傪巊偆偲偙傠偱偡丅偱偡偐傜扨埵傕丄倂倛乮儚僢僩傾儚乕乯傗倠倂倛乮僉儘儚僢僩傾儚乕乯偱偡丅侾帪娫偼俁俇侽侽昩偱偡偐傜丄侾倂倛偼俁俇侽侽倂昩乮俁俇侽侽俰乯偱偡丅
巹偨偪偑巟暐偆揹椡椏嬥傕丄揹椡検傪尦偵寛傔傜傟傑偡丅偮傑傝丄巊偭偨僄僱儖僊乕偺暘丄戙嬥傪庢傜傟傞栿偱偡丅
侾係.侾. 楙廗
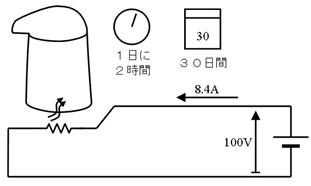
壓恾偺捠傝丄侾侽侽倁俉丏係俙偺僸乕僞傪丄枅擔俀帪娫丄俁侽擔娫摦嶌偝偣傞偲丄壗倠倂倛偺揹椡検傪徚旓偟傑偡偐丠
|
斣崋
|
崁栚
|
摎
|
|
嘆
|
僸乕僞偺揹椡
|
倂
|
|
嘇
|
俀帪娫摦嶌帪偺揹椡検
|
倠倂倛
|
|
嘊
|
俁侽擔娫摦嶌帪偺揹椡検
|
倠倂倛
|
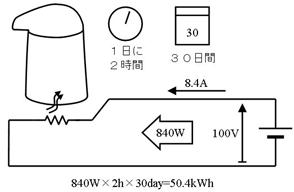
侾係.俀. 摎
|
斣崋
|
崁栚
|
摎
|
愢柧
|
|
嘆
|
僸乕僞偺揹椡
|
俉係侽倂
|
揹埑亊揹棳
|
|
嘇
|
俀帪娫摦嶌帪偺揹椡検
|
侾丏俇俉倠倂倛
|
揹椡亊帪娫
|
|
嘊
|
俁侽擔娫摦嶌帪偺揹椡検
|
俆侽丏係倠倂倛
|
堦擔揹椡検亊俁侽
|
侾俆. 僨僔儀儖乮倓俛乯
杮彂偱偼僨僔儀儖偼偟偽傜偔乮揱払娭悢偺偁偨傝傑偱偼乯弌偰偒傑偣傫丅傗傗偙偟偄妱傝偵偼巊偆婡夛偑彮側偄偱偡丅偙偺偨傔丄杮崁偼撉傒旘偽偟偰偍偒丄昁梫偑惗偠偰偐傜撉傓偙偲傕偱偒傑偡丅
偝偰丄僨僔儀儖偼乽揹椡偺攞棪偵晅偄偰偄傞僛儘偺悢傪悢偊偰侾侽攞偟偨傕偺乿傪昞偡扨埵偱偡丅乮偁偲偱徻偟偔愢柧偟傑偡乯乽揹椡偺攞棪乿偼乽棙摼乿傗乽僎僀儞乿偲傕屇傃傑偡丅
揹椡偺攞棪偼丄偨偲偊偽壓昞嘆乣嘊偺奃怓晹偱帵偡傛偆偵丄侾倂偑侾侽侽侽侽倂偵憹壛偡傟偽乽揹椡侾侽侽侽侽攞乿偱偡丅摉慠丄攞棪偼師偺傛偆偵寁嶼偱偒傑偡丅
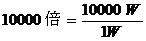 丂偮傑傝丄
丂偮傑傝丄
偲偙傠偑丄乽侾侽侽侽侽攞乿偲僛儘傪戲嶳彂偔偺偼柺搢偱偡偐傜丄壓昞嘋楍偺傛偆偵丄乽僛儘偺悢乿偩偗傪彂偔偙偲偵偟偰丄乽揹椡侾侽侽侽侽攞乿傪乽係[俛]乿乮儀儖乯偲屇傃傑偡丅揹椡侾侽侽攞側傜俀[俛]丄揹椡侾侽侽侽侽侽侽侽侽侽攞偱傕俋[俛]偲丄抁偔彂偔偙偲偑偱偒傑偡丅
|
嘆
|
嘇
|
嘊
|
嘋
|
嘍
|
|
擖椡
揹椡
|
弌椡
揹椡
|
揹椡偺
攞棪
|
攞棪偺0偺悢
[B]儀儖
|
0偺悢偺10攞
[dB]僨僔儀儖
|
|
1W
|
0.0001W
|
0.0001攞
|
-4 [B]
|
-40 [dB]
|
|
0.001W
|
0.001攞
|
-3 [B]
|
-30 [dB]
|
|
0.01W
|
0.01攞
|
-2 [B]
|
-20 [dB]
|
|
0.1W
|
0.1攞
|
-1 [B]
|
-10 [dB]
|
|
1W
|
1攞
|
0 [B]
|
0 [dB]
|
|
10W
|
10攞
|
1 [B]
|
10 [dB]
|
|
100W
|
100攞
|
2 [B]
|
20 [dB]
|
|
1000W
|
1000攞
|
3 [B]
|
30 [dB]
|
|
10000W
|
10000攞
|
4 [B]
|
40 [dB]
|
偟偐偟丄偁傑傝戝偒側攞棪偵側傞偲丄僛儘偺悢傪悢偊傞帠偝偊柺搢偱偡丅偙偺偨傔乽僛儘偺悢傪悢偊傞娭悢乿倢倧倗侾侽傪巊偄傑偡丅偨偲偊偽丄俤倶們倕倢偱僙儖偵=LOG(1000000000,10)偲擖椡偡傞偲丄乽俋乿偲昞帵偝傟傑偡丅幃偱彂偔偲丄
倢倧倗侾侽乮侾侽侽侽侽侽侽侽侽侽乯亖俋
偱偡丅偱偡偐傜丄揹椡偺攞棪偺僛儘偺悢[俛]乮儀儖偺抣乯偼丄僛儘傪悢偊傞娭悢倢倧倗侾侽傪巊偭偰丄
倢倧倗侾侽乮揹椡侾侽侽侽侽攞乯亖係[俛]
僄僋僙儖偱偼=LOG(10000,10)偲擖椡偡傟偽丄4偲昞帵偝傟傞丅
偮傑傝丄儀儖偺抣亖倢倧倗侾侽乮揹椡偺攞棪乯[俛]
偺傛偆偵偟偰寁嶼偱偒傑偡丅
偲偙傠偱丄侾[俛]憹偊傞偩偗偱丄侾侽攞傕戝偒偔側傞偺偼丄偪傚偭偲戝抇偡偓偰巊偄擄偄偱偡丅偨偲偊偽丄乽侾[俛]戝惙傝偵偟偰偔傟乿偲棅傓偲丄侾侽恖慜偺戝惙傝偑弌偰偔傞乿栿偱偡丅
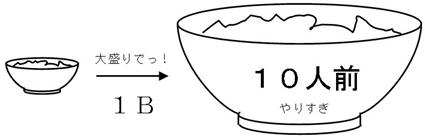
偦偙偱丄忋昞嘍楍偺傛偆偵丄侾侽[倓俛]偱侾[俛]偲側傞扨埵丄[倓俛]乮僨僔儀儖乯傪巊偄傑偡丅侾侽攞偵偟偨偩偗偱偡偐傜丄揹椡侾侽侽侽侽攞偺応崌偼師偺傛偆偵寁嶼偱偒傑偡丅
侾侽亊倢倧倗侾侽乮揹椡侾侽侽侽侽攞乯亖係侽倓俛
僄僋僙儖偱偼=10*LOG(10000,10)偲擖椡偡傟偽40偲昞帵偝傟傞丅
偮傑傝丄僨僔儀儖偺抣亖侾侽亊倢倧倗侾侽乮揹椡偺攞棪乯[倓俛]
俛乮儀儖乯偺戙傢傝偵倓俛乮僨僔儀儖乯傪巊偆偺偼丄侾丏俀[俴]乮儕僢僩儖乯偲屇傇戙傢傝偵丄抣傪侾侽攞偟偰丄侾俀[倓俴]乮僨僔儕僢僩儖乯偲屇傇偺偲摨偠偱偡丅
侾[俛]偼侾侽攞偱偡偑丄侾[倓俛]偼栺侾丏俀俇攞偱偡丅侾[倓俛]偺戝惙傝偼丄俀俇亾憹検偱偡丅俁[倓俛]側傜俀攞惙傝丄偙傟側傜丄巊偄彑庤偑椙偝偦偆偱偡丅
侾俆.侾. 楙廗
侾倣倂傪憹暆婍偵擖椡偟偨偲偙傠丄侾侽倂偑弌椡偝傟偨丄棙摼偼壗倓俛偐
侾俆.俀. 摎
僄僋僙儖偱=10*LOG(10/1E-3,10)偲擖椡偟偰丄棙摼偼40dB丂丂
乮1E-3偼1m偺堄枴丄1E3側傜1k偺堄枴乯
侾俇. 敿抂側悢偺僨僔儀儖
偝偰丄侾侽侽攞側傜乽僛儘俀偮乿偲悢偊傜傟傑偡偑丄椺偊偽俁侽攞偼偳偆偱偟傚偆丅俁侽攞偼丄侾侽攞乮侾屄乯傛傝偼戝偒偄偟丄侾侽侽攞乮俀屄乯傛傝偼彫偝偄偲巚傢傟傑偡丅岾偄丄倢倧倗侾侽偼偙偺傛偆側応崌偵傕摎傪弌偟偰偔傟傑偡丅
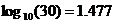
僄僋僙儖偱偼=LOG(30,10)偲擖椡
偮傑傝丄俁侽攞偺僛儘偺屄悢偼侾丏俆屄掱搙偱丄妋偐偵侾傛傝戝偒偔俀傛傝彫偝偄偱偡丅
侾俇.侾. 楙廗
侾丏俆倣倂傪憹暆婍偵擖椡偟偨偲偙傠丄侾侽侽倂偑弌椡偝傟偨丄棙摼偼壗倓俛偐
侾俇.俀. 摎
僄僋僙儖偱=10*LOG(100/1.5E-3,10)偲擖椡偟偰丄棙摼偼栺48.2dB
侾俈. 揹埑偺僨僔儀儖
壓恾偺夞楬偱丄揹埑傪侾侽攞丄侾侽侽攞丄偲戝偒偔偡傞偲丄揹棳傕侾侽攞丄侾侽侽攞偲憹壛偟傑偡丅偦偺寢壥丄揹椡偼丄侾侽侽攞丄侾侽侽侽侽攞偲揹埑埲忋偺惃偄偱戝偒偔側傝傑偡丅
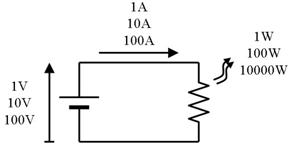
偮傑傝丄壓昞拝怓晹偱帵偡傛偆偵丄揹埑偺攞棪偺僛儘偺悢偑丄侾丄俀丄俁乧偲憹壛偡傞偲丄揹椡偺攞棪偺僛儘偺悢乮儀儖偺抣乯偼丄俀丄係丄俇乧偲俀攞偺儁乕僗偱戝偒偔側傝傑偡丅
|
揹埑
|
揹椡
|
|
攞棪
|
攞棪偺0偺悢
|
攞棪
|
攞棪偺0偺悢
[B]儀儖
|
0偺悢偺10攞
[dB]僨僔儀儖
|
|
0.1攞
|
-1
|
0.01攞
|
-2[B]
|
-20[dB]
|
|
1攞
|
0
|
1攞
|
0[B]
|
0[dB]
|
|
10攞
|
1
|
100攞
|
2[B]
|
20[dB]
|
|
100攞
|
2
|
10000攞
|
4[B]
|
40[dB]
|
|
1000攞
|
3
|
1000000攞
|
6[B]
|
60[dB]
|
揹埑偺攞棪偑侾侽侽侽攞偺偲偒丄揹椡偺攞棪偼侾侽侽侽侽侽侽攞偵側傝傑偡丅偙偺偨傔揹埑偺攞棪侾侽侽攞偐傜儀儖偺抣傪媮傔傞偵偼丄僛儘偺悢傪俀攞偟偰丄
俀亊倢倧倗侾侽乮揹埑侾侽侽侽攞乯亖俀亊俁亖俇[俛]
俤倶們倕倢偱偼=2*log(1000,10)偲擖椡偡傟偽6[B]偲昞帵偝傟傞丅
偮傑傝丄儀儖偺抣亖俀亊倢倧倗侾侽乮揹埑偺攞棪乯[俛]
偲寁嶼偟傑偡丅
揹埑偺攞棪偐傜乽倓俛偺抣乿傪媮傔傞応崌偼丄乽俛偺抣乿傪侾侽攞偡傟偽椙偄偺偱丄
侾侽亊俀亊倢倧倗侾侽乮揹埑侾侽侽侽攞乯亖侾侽亊俀亊俁亖俇侽[倓俛]
俤倶們倕倢偱偼=20*log(1000/1,10)偲擖椡偡傟偽60[dB]偲昞帵偝傟傞丅
偮傑傝丄僨僔儀儖偺抣亖俀侽亊倢倧倗侾侽乮揹埑偺攞棪乯[倓俛]
偲寁嶼偟傑偡丅
偙偺傛偆偵丄揹埑偐傜倓俛傪媮傔傞偲偒偵弌偰偔傞俀侽偼丄儀儖偵偡傞偨傔偺侾侽偲丄揹埑斾傪揹椡斾偵偡傞偨傔偺俀偑崌傢偝偭偨傕偺偱偡丅
侾俈.侾. 楙廗
侾丏俆倣倁傪憹暆婍偵擖椡偟偨偲偙傠丄侾侽侽倁偑弌椡偝傟偨丄棙摼偼壗倓俛偐
侾俈.俀. 摎
僄僋僙儖偱=20*LOG(100/1.5E-3,10)偲擖椡偟偰丄棙摼偼栺96.5dB
侾俉. 僨僔儀儖偐傜揹椡偺攞棪傪媮傔傞
偨偲偊偽揹椡侾侽侽侽侽攞偺僛儘偺屄悢乮儀儖偺抣乯係偼丄師偺傛偆偵寁嶼偱偒傑偟偨丅
倢倧倗侾侽乮侾侽侽侽侽攞乯亖僛儘係屄
偮傑傝丄儀儖偺抣亖倢倧倗侾侽乮揹椡偺攞棪乯
媡偵丄僛儘偺屄悢乮偮傑傝丄係乵俛乶乯偐傜丄揹椡侾侽侽侽侽攞偼丄
侾侽係亖侾侽侽侽侽攞
僄僋僙儖偱偼丄=10^4偁傞偄偼=POWER(10,4)偲擖椡偡傟偽10000攞偲昞帵偝傟傞丅
偮傑傝丄揹椡偺攞棪亖侾侽儀儖偺抣
偱媮傔傞偙偲偑偱偒傑偡丅
偝偰丄係侽乵倓俛乶偼係乵俛乶偱偟偨偐傜丄揹椡偺攞棪傪係侽乵倓俛乶偐傜媮傔傞偲偒偼丄僨僔儀儖偺抣傪侾侽偱妱偭偰丄僛儘偺屄悢傪媮傔偰丄
侾侽係侽亐侾侽亖侾侽侽侽侽攞
僄僋僙儖偱偼丄=10^(40/10)偁傞偄偼=POWER(10,40/10)偲擖椡偡傟偽10000攞偲昞帵偝傟傞丅
偮傑傝丄揹椡偺攞棪
亖侾侽僨僔儀儖偺抣亐侾侽
偲寁嶼偱偒傑偡丅
侾俉.侾. 楙廗
俀俇倓俛偺棙摼偺偁傞憹暆婍偵俀俀倣倂偺怣崋傪擖椡偟偨丄弌椡偼壗倂偲側傞偐
侾俉.俀. 摎
揹椡偺攞棪傪俀俇倓俛偐傜媮傔偰丄俀俀倣倂偵妡偗傟偽傛偄丄偮傑傝僄僋僙儖偱=22E-3*10^(26/10)偲擖椡偟偰丄栺8.76W
侾俋. 僨僔儀儖偐傜揹埑偺攞棪傪媮傔傞
係侽乵倓俛乶乮係乵俛乶乯側傜揹椡偼侾侽侽侽侽攞丄揹埑偼侾侽侽攞偱偟偨丅偮傑傝丄揹椡偺僛儘偺悢傪敿暘偵尭傜偡偲揹埑偺攞棪偵側傝傑偟偨丅偦偺偨傔丄揹椡偑係侽乵倓俛乶偺偲偒揹埑偺攞棪偼丄
侾侽係侽亐侾侽亐俀亖揹埑侾侽侽攞
僄僋僙儖偱偼丄=10^(40/20)偁傞偄偼=POWER(10,40/20)偲擖椡偡傟偽100攞偲昞帵偝傟傞丅
偮傑傝丄揹埑偺攞棪亖侾侽僨僔儀儖偺抣亐俀侽
偲寁嶼偱偒傑偡丅
侾俋.侾. 楙廗
俀俇倓俛偺棙摼偺偁傞憹暆婍偵俀俀倣倁偺怣崋傪擖椡偟偨丄弌椡偼壗倁偲側傞偐
侾俋.俀. 摎
俀俇倓俛偺揹埑偺攞棪偼丄僄僋僙儖偱=10^(26/20)攞丄俀俀倣倁傪擖椡偟偨偲偒偺弌椡揹埑偼丄僄僋僙儖偱=22E-3*10^(26/20)偲擖椡偟偰丄栺439mV
俀侽. 僨僔儀儖偺栚埨
壓昞偺僨僔儀儖抣偼丄愗傝偺椙偄攞棪偵側傞偺偱丄栚埨偲偟偰棙梡偱偒傑偡丅
|
僨僔儀儖
|
揹椡
|
揹埑
|
|
侾倓俛
|
栺侾丏俀俇攞
|
栺侾丏侾俀攞
|
|
俁倓俛
|
栺俀攞
|
栺侾丏係侾攞
|
|
俇倓俛
|
栺係攞
|
栺俀攞
|
|
俈倓俛
|
栺俆攞
|
栺俀丏俀係攞
|
|
俋倓俛
|
栺俉攞
|
栺俀丏俆侾
|
|
侾侽倓俛
|
侾侽攞
|
栺俁丏侾俇攞
|
侾侽丄侾侽侽丄侾侽侽侽攞偺僨僔儀儖偼丄侾侽丄俀侽丄俁侽偲暘傞偺偱丄忋昞偲慻傒崌傢偣偰條乆側抣偱栚埨傪抦傞偙偲偑偱偒傑偡丅
倓俛偺懌嶼偼丄攞棪偺妡偗嶼偵側傝丄攞棪偺妡偗嶼偼丄倓俛偺懌嶼偵側傝傑偡丅偙偺偨傔壓昞偺椺偱偼丄俁俁倓俛偺応崌丄俁侽倓俛亄俁倓俛偲峫偊偰丄俁侽倓俛仺侾侽侽侽攞丄忋昞傛傝俁倓俛仺俀攞偱偡偐傜丄侾侽侽侽攞亊俁攞偱俀侽侽侽攞偲奣嶼偱偒傑偡丅
|
僨僔儀儖偺悽奅
偨偟嶼
|
俁俁倓俛
|
|
俁侽倓俛
|
亄
|
俁倓俛
|
|
攞棪偺悽奅
妡偗嶼
|
侾侽侽侽攞
|
亊
|
俀攞
|
|
俀侽侽侽攞
|
媡偵丄揹椡俀侽侽侽攞偺応崌丄俀攞亊侾侽侽侽攞偲峫偊偰丄俀攞仺俁倓俛丄侾侽侽侽攞仺俁侽倓俛偱偡偐傜丄俁倓俛偲俁侽倓俛傪壛偊偰丄俁俁倓俛偲奣嶼偱偒傑偡丅
俀侽.侾. 栤戣
師偺昞偺丂丂丂丂偵揔愗側奣嶼抣傪婰擖偟偰丄昞傪姰惉偟偰壓偝偄丅
|
僨僔儀儖
|
揹椡
|
|
俁俁倓俛
|
俀侽侽侽攞
|
|
俀俋倓俛
|
丂丂丂丂攞
|
|
侾俇倓俛
|
丂丂丂丂攞
|
|
丂丂丂丂倓俛
|
俆侽攞
|
|
丂丂丂丂倓俛
|
俉侽侽侽攞
|
俀侽.俀. 摎
|
僨僔儀儖
|
揹椡
|
峫偊曽
|
|
俁俁倓俛
|
俀侽侽侽攞
|
俁侽亄俁倓俛佁侾侽侽侽攞亊俀攞
|
|
俀俋倓俛
|
丂俉侽侽攞
|
俀侽亄俋倓俛佁侾侽侽攞亊俉攞
|
|
侾俇倓俛
|
丂丂係侽攞
|
侾侽亄俇倓俛佁侾侽攞亊係攞
|
|
丂丂侾俈倓俛
|
俆侽攞
|
侾侽亄俈倓俛佁侾侽攞亊俆攞
|
|
丂丂俁俋倓俛
|
俉侽侽侽攞
|
俁侽亄俋倓俛佁侾侽侽侽攞亊俉攞
|
侾. 岎棳夞楬
壠掚偺僐儞僙儞僩偵揹媴傪愙懕偡傞偲丄壓恾偵帵偡傛偆側丄岦偒傗戝偒偝偑乮帪偲嫟偵乯扨弮側曄壔傪孞傝曉偡乮僽儖僽儖恔偊傞傛偆側乯揹棳偑棳傟傑偡丅偙偺傛偆側揹棳傗揹埑傪乽岎棳乿偲屇傃丄偙偺傛偆側揹棳偑棳傟傞夞楬傪乽岎棳夞楬乿偲屇傃傑偡丅
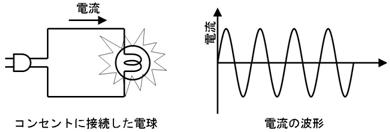
俀. 岎棳偲廃攇悢
壓恾偵捈棳乮揰慄乯偲岎棳乮幚慄乯傪帵偟傑偡丅堦掕偱曄壔偟側偄揹埑傗揹棳偑乽捈棳乿丄扨弮側曄壔傪孞傝曉偡揹埑傗揹棳偑乽岎棳乿偱偡丅
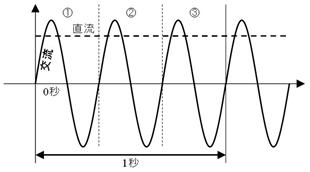
捈棳偲岎棳
傑偨丄侾昩娫偵傗偭偰棃偨攇偺悢傪乽廃攇悢乿偲屇傃丄扨埵偼俫倸乮僿儖僣乯偱偡丅忋偺恾偱偼侾昩娫偵俁屄偺攇偑棃偰偄傞偺偱丄廃攇悢偼俁俫倸偱偡丅
俁. 岎棳偺嫮偝乮岎棳揹埑乯
捈棳偺侾倁乮侾倁俢俠乯偱傕丄岎棳偺侾倁乮侾倁俙俠乯偱傕丄摨偠侾倁偱偡偐傜丄揹媴偑摨偠柧傞偝偱岝傞敜偱偡丅
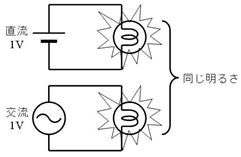
壓恾偺傛偆偵丄岎棳偺壓懁傪丄忋懁偵愜傝曉偟偰丄捈棳偲嫮偝傪斾傋偰傒傑偟傚偆丅壓恾偵帵偡丄嵟戝揹埑偑侾倁偺岎棳偼丄恾偵怓傪揾偭偨晹暘偑捈棳傛傝庛偔丄偦偺寢壥丄揹媴偼捈棳傛傝埫偔岝傝傑偡丅偱偡偐傜丄偙偺傛偆側嵟戝揹埑侾倁偺岎棳偼丄侾倁偺岎棳偲偼屇傋傑偣傫丅
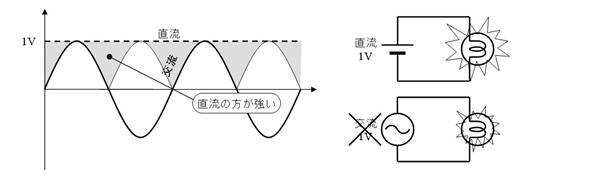
偦偙偱丄俀偮偺揹媴偑摨偠柧傞偝偱岝傞傛偆偵岎棳偺嫮偝傪挷愡偡傞偲丄壓恾偺傛偆偵側傝傑偟偨丅
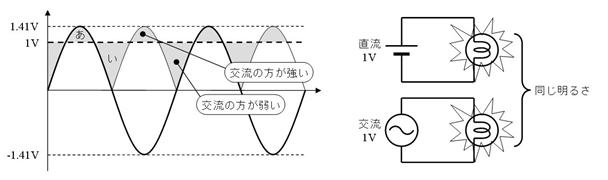
忋恾乽偁乿偺晹暘偱丄岎棳偑捈棳傛傝嫮偔丄岎棳偑捈棳傛傝庛偄乽偄乿偺晹暘傪懪偪徚偟偰丄捈棳偲岎棳偺嫮偝偑摨偠偵側傝傑偡丅
偙偺偲偒丄岎棳偺嵟戝揹埑偼侾丏係侾倁乮偮傑傝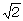 倁乯偱偡丅偙偺傛偆側岎棳傪乽侾倁偺岎棳乿偲屇傃傑偡丅
倁乯偱偡丅偙偺傛偆側岎棳傪乽侾倁偺岎棳乿偲屇傃傑偡丅
偮傑傝丄岎棳偺揹埑傪丄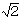 攞乮侾丏係侾攞乯偡傞偲丄岎棳偺嵟戝揹埑傪媮傔傞偙偲偑偱偒丄媡偵丄岎棳偺嵟戝揹埑傪丄
攞乮侾丏係侾攞乯偡傞偲丄岎棳偺嵟戝揹埑傪媮傔傞偙偲偑偱偒丄媡偵丄岎棳偺嵟戝揹埑傪丄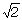 乮侾丏係侾乯偱妱傞偲丄岎棳偺揹埑傪媮傔傞偙偲偑偱偒傑偡丅
乮侾丏係侾乯偱妱傞偲丄岎棳偺揹埑傪媮傔傞偙偲偑偱偒傑偡丅
岎棳偺揹埑偵偼壓昞偺傛偆偵丄暋悢偺屇傃曽傗彂偒曽偑偁傝傑偡丅
|
屇傃曽偺
怓乆
|
岎棳揹埑
俙俠揹埑
幚岠抣揹埑
|
|
彂偒曽偺
怓乆
|
俙俠侾侽倁
侾侽倁俙俠
侾侽倁俼俵俽
|
係. 僺乕僋丒僩僁丒僺乕僋揹埑
壓恾偼侾侽倁偺岎棳偺椺偱偡丅嵟戝揹埑偼侾係丏侾倁丄嵟彫揹埑偼亅侾係丏侾倁偱偡丅
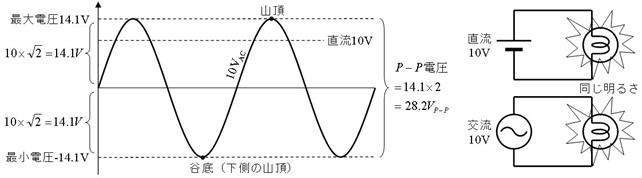
扟掙乮壓懁偺嶳捀乯偐傜丄嶳捀傑偱偺揹埑偼丄乮僆僔儘摍偱乯娙扨偵應掕偱偒傞偺偱丄岲傫偱巊梡偝傟丄僺乕僋丒僩僁丒僺乕僋乮嶳捀偐傜嶳捀傑偱偺乯揹埑乮俹亅俹揹埑乯偲屇偽傟傑偡丅忋恾偵帵偡侾侽倁俙俠偺岎棳偺僺乕僋丒僩僁丒僺乕僋揹埑偼丄俀俉丏俀倁俹亅俹偱偡丅岎棳偺揹埑偵丄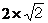 傪妡偗傞偲乮俀丏俉俀傪妡偗傞偲乯僺乕僋丒僩僁丒僺乕僋揹埑傪媮傔傞偙偲偑偱偒傑偡丅
傪妡偗傞偲乮俀丏俉俀傪妡偗傞偲乯僺乕僋丒僩僁丒僺乕僋揹埑傪媮傔傞偙偲偑偱偒傑偡丅
揹棳偺応崌傕揹埑偲摨條偵丄侾俙偲摨偠嫮偝偺岎棳揹棳偺嵟戝抣偼丄侾丏係侾俙乮偮傑傝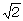 俙乯丄偙偺偲偒偺俹亅俹揹棳偼俀丏俉俀俙乮偮傑傝 2 亊
俙乯丄偙偺偲偒偺俹亅俹揹棳偼俀丏俉俀俙乮偮傑傝 2 亊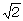 俙乯偱偡丅
俙乯偱偡丅
壓恾偼俀倁偺岎棳偱偡丅偙偺岎棳偺丄廃攇悢丄嵟戝揹埑丄嵟彫揹埑丄俹亅俹揹埑傪摎偊偰偔偩偝偄丅
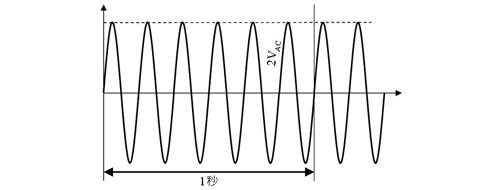
廃攇悢丂丂丂俫倸丄嵟戝揹埑丂丂丂丂丂倁丄嵟彫揹埑丂丂丂丂丂倁丄俹亅俹揹埑丂丂丂丂丂倁俹亅俹
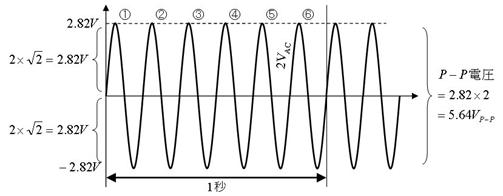
廃攇悢丂丂俇俫倸丄嵟戝揹埑丂俀丏俉俀倁丄嵟彫揹埑亅俀丏俉俀倁丄俹亅俹揹埑丂俆丏俇係倁俹亅俹
壓恾偼侾侾丏俁倁俹亅俹偺岎棳偱偡丅偙偺岎棳偺丄廃攇悢丄嵟戝揹埑丄嵟彫揹埑丄岎棳偺揹埑傪摎偊偰偔偩偝偄丅
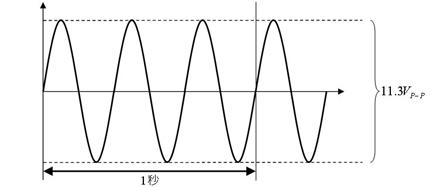
廃攇悢丂丂丂俫倸丄嵟戝揹埑丂丂丂丂丂倁丄嵟彫揹埑丂丂丂丂丂倁丄岎棳偺揹埑丂丂丂丂丂倁俙俠
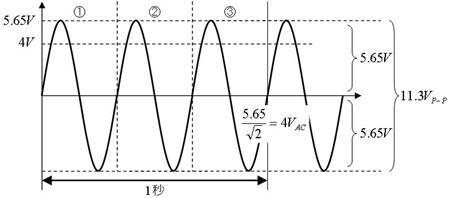
廃攇悢丂丂俁俫倸丄嵟戝揹埑丂俆丏俇俆倁丄嵟彫揹埑亅俆丏俇俆倁丄岎棳偺揹埑丂丂丂係倁倁俙俠
俆. 岎棳揹埑傗揹棳偺寁嶼
岎棳揹埑偵偼丄嵟戝揹埑傗岎棳揹埑丄俹亅俹乮僺乕僺乕乯揹埑偲偄偆暋悢偺帵偟曽偑偁傝傑偡丅揹棳傕摨條偱偡丅揹埑傗揹棳傪寁嶼偡傞応崌偼丄摨偠帵偟曽偵摑堦偟偰寁嶼偟傑偡丅椺偊偽丄
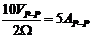
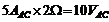
偲偄偆姶偠偱偡丅偱偡偐傜丄
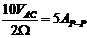 丂仼岆傝
丂仼岆傝
偼娫堘偄偱偡丅
壓恾偺夞楬偵棳傟傞俹亅俹揹棳偲丄俙俠揹棳傪媮傔偰偔偩偝偄丅
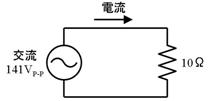
俹亅俹揹棳丂丂丂丂丂丂丂丄俙俠揹棳丂丂丂丂丂丂丂倶
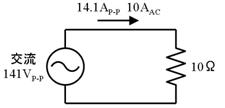
俹亅俹揹棳丂侾係丏侾俙俹亅俹丄俙俠揹棳丂丂丂侾侽俙俙俠倶
俹亅俹揹棳偼丄乮摨偠拠娫偺乯俹亅俹揹埑偐傜捈愙媮傔傞偙偲偑偱偒傑偡丅俙俠揹棳偼俹亅俹揹棳傪併俀偱妱偭偰媮傔傑偡丅
俇. 岎棳偺乽棳傟擄偝乿偲乽棳傟堈偝乿
掞峈偵偼丄捈棳傪壛偊偰傕丄岎棳傪壛偊偰傕丄摨偠戝偒偝偺揹棳偑棳傟傑偡丅偟偐偟丄壓恾偺僐儞僨儞僒偼丄捈棳偱偼揹棳偼棳傟傑偣傫偑丄岎棳側傜揹棳偑棳傟傑偡丅偙偺偨傔丄岎棳偺乽棳傟擄偝乿傗乽棳傟堈偝乿偼丄岎棳傪巊偭偰應掕偟丄捈棳偱應掕偟偨傕偺乮乽掞峈乿傗乽僐儞僟僋僞儞僗乿乯偲嬫暿偡傞昁梫偑偁傝傑偡丅
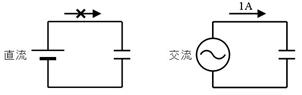
偦偙偱丄壓昞偵帵偡偲偍傝丄岎棳偱應掕偟偨乽棳傟擄偝乿傗乽棳傟堈偝乿傪乽僀儞僺乕僟儞僗乿傗乽傾僪儈僞儞僗乿偲屇傃傑偡丅
|
怣崋
|
捈棳
|
岎棳
|
|
暘椶
|
棳傟擄偝
|
棳傟堈偝
|
棳傟擄偝
|
棳傟堈偝
|
|
柤慜
|
掞峈
|
僐儞僟僋僞儞僗
|
僀儞僺乕僟儞僗
|
傾僪儈僞儞僗
|
|
扨埵
|
兌乮僆乕儉乯
|
俽乮僕乕儊儞僗乯
|
兌乮僆乕儉乯
|
俽乮僕乕儊儞僗乯
|
|
椺
|
係兌
|
侽丏俀俆俽
|
係兌
|
侽丏俀俆俽
|
|
媮傔曽
|

|

|

|

|
掞峈偺媡悢偑僐儞僟僋僞儞僗偵側偭偨傛偆偵丄僀儞僺乕僟儞僗偺媡悢偑傾僪儈僞儞僗偵側傝傑偡丅
壓昞偺嬻棑晹傪偵揔愗側撪梕傪婰擖偟丄捈棳丒岎棳偺壗傟偐偲丄棳傟堈偝丒棳傟擄偝偺壗傟偐傪慖傫偱壓偝偄丅
|
|
掞峈
|
僐儞僟僋僞儞僗
|
傾僪儈僞儞僗
|
僀儞僺乕僟儞僗
|
|
扨埵
|
|
|
|
|
|
扨埵偺屇傃曽
|
|
|
|
|
|
媮傔曽
|
|
|
|
|
|
岎捈偺暿
|
捈棳丒岎棳
|
捈棳丒岎棳
|
捈棳丒岎棳
|
捈棳丒岎棳
|
|
棳傟偺擄堈
|
堈偝丒擄偝
|
堈偝丒擄偝
|
堈偝丒擄偝
|
堈偝丒擄偝
|
|
|
掞峈
|
傾僪儈僞儞僗
|
僀儞僺乕僟儞僗
|
僐儞僟僋僞儞僗
|
|
扨埵
|
兌
|
俽
|
兌
|
俽
|
|
扨埵偺屇傃曽
|
僆乕儉
|
僕乕儊儞僗
|
僆乕儉
|
僕乕儊儞僗
|
|
媮傔曽
|

|

|

|

|
|
岎捈偺暿
|
捈棳丒岎棳
|
捈棳丒岎棳
|
捈棳丒岎棳
|
捈棳丒岎棳
|
|
棳傟偺擄堈
|
堈偝丒擄偝
|
堈偝丒擄偝
|
堈偝丒擄偝
|
堈偝丒擄偝
|
俈. 岎棳偲僆乕儉偺朄懃
僆乕儉偺朄懃偼岎棳偱傕偦偺傑傑巊偊傑偡丅夞楬偵壛傢傞揹埑傪丄夞楬偵棳傟偨揹棳偱妱傟偽丄僀儞僺乕僟儞僗偺戝偒偝乮偟偽傜偔偼丄扨偵乽僀儞僺乕僟儞僗乿偲屇傃傑偡乯傪媮傔傞偙偲偑偱偒傑偡丅
乮岎棳偺乯僀儞僺乕僟儞僗偵偼乮捈棳偺乯掞峈偲偼堘偆丄晄巚媍側惈幙傕偁傝傑偡偑丄偙偺揰偼屻偱愢柧偡傞偲偟偰丄愭偢偼丄捈棳偲摨偠傛偆偵峫偊傞偙偲偑偱偒傞乽僀儞僺乕僟儞僗偺戝偒偝乿偵偮偄偰愢柧偟傑偡丅
壓恾偺夞楬偺丄僐儞僨儞僒偲僐僀儖偺僀儞僺乕僟儞僗傪媮傔偰偔偩偝偄丅
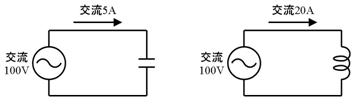
僐儞僨儞僒丂丂丂兌丂丂丂丂丂丂丂丂僐僀儖丂丂丂兌
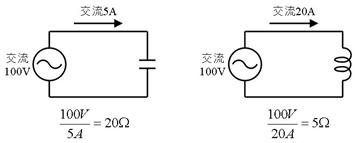
僐儞僨儞僒丂俀侽兌丂丂丂丂丂丂丂丂僐僀儖丂俆丂兌
壓恾偺夞楬偺揰慄偱埻傫偩晹暘偺僀儞僺乕僟儞僗偲傾僪儈僞儞僗傪媮傔偰偔偩偝偄丅
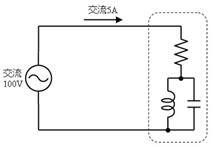
僀儞僺乕僟儞僗丂丂丂丂兌丄傾僪儈僞儞僗丂丂丂丂俽
俈.係. 摎
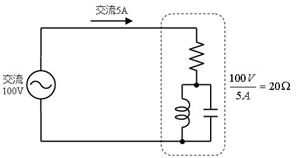
僀儞僺乕僟儞僗丂俀侽丂兌丄傾僪儈僞儞僗侽丏侽俆俽
夞楬偺撪晹偑暋嶨側傕偺偱偁偭偰傕丄壛偊偨揹埑偲棳傟偨揹棳偐傜僀儞僺乕僟儞僗傪媮傔傞偙偲偑偱偒傑偡丅
俉. 俴俠偺僀儞僺乕僟儞僗偲傾僪儈僞儞僗
晹昳揦偵峴偭偰乽侾侽兌偺僐儞僨儞僒傪壓偝偄乿偲尵偭偰傕丄乽偦傟偼掞峈偱偟傚偆乿偲徫傢傟傞偩偗偱偡丅僐儞僨儞僒傪僀儞僺乕僟儞僗傪乮侾侽兌摍偲乯傪巜掕偟偰峸擖偱偒側偄偺偼丄摨偠戝偒偝偺僐儞僨儞僒偱傕廃攇悢偑曄傢傞偲僀儞僺乕僟儞僗偑曄傢偭偰偟傑偆偐傜偱偡丅僐僀儖傕摨條偱偡丅
偱偡偐傜丄僐僀儖乮俴乯偲僐儞僨儞僒乮俠乯偺僀儞僺乕僟儞僗乮棳傟擄偝乯傗傾僪儈僞儞僗乮棳傟堈偝乯偼丄愭偵廃攇悢傪寛傔偰偐傜丄僐僀儖傗僐儞僨儞僒偺戝偒偝傪尦偵寁嶼偡傞昁梫偑偁傝傑偡丅
寁嶼偺曽朄傪壓昞偵帵偟傑偡丅昞拞偺俴偼丄僐僀儖偺戝偒偝[俫]乮僿儞儕乕乯丄俠偼僐儞僨儞僒偺戝偒偝[俥]乮僼傽儔僪乯丄倖偼巊梡偡傞廃攇悢[俫倸]偱偡丅
廃攇悢偲僀儞僺乕僟儞僗
|
|
僀儞僺乕僟儞僗
岎棳偺捠偟擄偝
|
傾僪儈僞儞僗
岎棳偺捠偟擄偝
|
|
僐儞僨儞僒俠
|
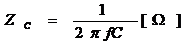
=1/2/PI()/F1/C1
|
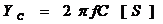
=2*PI()*F1*C1
|
|
僐僀儖俴
|
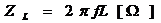
=2*PI()*F1*L1
|
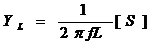
=1/2/PI()/F1/L1
|
椺偊偽丄廃攇悢倖亖俁侾俉俫倸丄僐僀儖偺戝偒偝俴亖侾侽倣俫乮侽丏侽侾俫乯偺応崌丄僐僀儖偺僀儞僺乕僟儞僗乮岎棳偺棳傟擄偝乯倅俴偼
倅俴亖俀兾倖俴亖俀亊俁丏侾係亊俁侾俉亊侽丏侽侾亖俀侽[兌]
=2*PI()*318*10E-3
偲寁嶼偟傑偡丅
僐僀儖偺僀儞僺乕僟儞僗偲丄夞楬偵棳傟傞岎棳揹棳傪媮傔偰偔偩偝偄丅偨偩偟岎棳偺廃攇悢偼俇丏俁俈俫倸偲偟傑偡丅
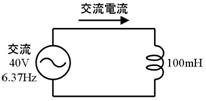
僀儞僺乕僟儞僗丂丂丂兌丄夞楬偵棳傟傞岎棳揹棳丂丂丂俙
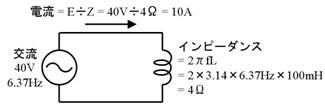
僀儞僺乕僟儞僗丂係丂兌丄夞楬偵棳傟傞岎棳揹棳丂侾侽俙
侾. 岎棳夞楬偺抦幆偼昁梫偐
岎棳夞楬偺抦幆乮岎棳棟榑乯側傫偰抦傜側偔偰傕丄怓乆側揹巕夞楬偑嶌傟傑偡丅摿偵僆儁傾儞僾傪巊偭偨掅廃攇偺夞楬傗儅僀僐儞傪拞怱偵偟偨夞楬偱偼丄岎棳棟榑偺抦幆偼偁傑傝昁梫偱偼偁傝傑偣傫丅偦偺傛偆側応崌偼杮復傪撉傒旘偽偟偰丄堦婥偵乽傾僫儘僌夞楬擖栧乿偵恑傔偽椙偄偱偟傚偆丅
偟偐偟丄椺偊偽柍愙揰媼揹夞楬側偳偺僐僀儖傗嫟怳傪棙梡偡傞岺嶌傗丄僼傿儖僞丄崅廃攇傪埖偆岺嶌偱偼岎棳棟榑偺抦幆偑昁梫偵側傝傑偡丅傑偨丄儅僀僐儞傪棙梡偟偨惂屼憰抲偱偼丄岎棳棟榑傪敪揥偝偣偨惂屼棟榑偺抦幆偑栶棫偪傑偡丅偮傑傝丄岎棳棟榑偑暘偭偰偄傞偲乽偪傚偭偲婸偔揹巕岺嶌乿偑嶌傟傞傛偆偵側傝傑偡丅
偲偙傠偑丄妛峑偺嫵壢彂偺岎棳棟榑偼乽惓妋偡偓偰暘傝擄偄乿偨傔丄乮岎棳棟榑偺棟夝偼掹傔偰乯岎棳棟榑偑昁梫側偄斖埻偱揹巕岺嶌傪妝偟傫偱偍傜傟傞曽傕懡偄偲巚偄傑偡丅
偙傟偵懳偟偰丄妛峑偺嫵壢彂偵挦傝偰岎棳棟榑傪掹傔偨曽偵傕棟夝捀偗傞傛偆偵岺晇偟偰偄傑偡丅乽晄惓妋偱傕暘偐傝堈偄乿愢柧傪揙掙偟丄恎嬤側乽偨偲偊榖乿傪懡梡偟偰丄岎棳偺怳傞晳偄偑姶偠傜傟傞傛偆偵愢柧偟偰偄傑偡丅
杮彂偺晄惓妋側愢柧偱偁偭偰傕丄偦傟偱堦扷棟夝偟偰偟傑偊偽彑偪偱丄戝妛偺嫵壢彂偩偭偰乽偁偁丄偁偺帠偐乿乽偙傫側帠傪丄傛偔傕傑偁丄偙傫側偵擄偟偔彂偄偨傕傫偩側偀乧乿偲僗儔僗儔撉傔傞傛偆偵側傝傑偡丅
俀. 晄巚媍側尰徾偲岎棳棟榑偺悽奅
偝偰偙偙傑偱偼丄僀儞僺乕僟儞僗傪巊偭偰丄岎棳夞楬偱傕丄捈棳夞楬偲摨條偵僆乕儉懃偑巊偊傞帠傪愢柧偟偰棃傑偟偨丅
偟偐偟丄岎棳撈摿偺晄巚媍側尰徾傕敪惗偟傑偡丅椺偊偽丄壓恾偺夞楬偱偼丄俆兌偺僐僀儖偲丄係兌偺僐儞僨儞僒傪捈楍偵宷偄偩偲偙傠丄慡懱偲偟偰侾兌偲側傝丄俋倁偺岎棳傪壛偊偨傜丄俋俙傕偺揹棳偑棳傟傑偟偨丅
俆兌傕丄係兌傕丄乽捠偟擄偝乿側偺偵丄俀偮捈楍偵偡傞偲丄媡偵乽棳傟堈偔側傞乿偲偄偆晄巚媍側尰徾偑婲偒偰偄傑偡丅
偙偙偱乽捈楍夞楬偺僀儞僺乕僟儞僗偼
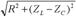 偩偐傜乧乿偲棟桼傪峫偊偢偵岞幃傪帩偪弌偟偰偼愭乆墳梡偑棙偐側偔側偭偰偟傑偄傑偡丅偦傟偱偼乽岞幃傪妎偊偰偄傞偩偗乿偱丄僀儞僺乕僟儞僗偺惓懱傪姶偠偨帠偵偼側傜側偄偐傜偱偡丅乮揹巕岺嶌偵墳梡偟偰丄柺敀偄夞楬傪敪憐偡傞偵偼乽惓懱傪姶偠傞乿帠偑戝愗偱偡乯
偩偐傜乧乿偲棟桼傪峫偊偢偵岞幃傪帩偪弌偟偰偼愭乆墳梡偑棙偐側偔側偭偰偟傑偄傑偡丅偦傟偱偼乽岞幃傪妎偊偰偄傞偩偗乿偱丄僀儞僺乕僟儞僗偺惓懱傪姶偠偨帠偵偼側傜側偄偐傜偱偡丅乮揹巕岺嶌偵墳梡偟偰丄柺敀偄夞楬傪敪憐偡傞偵偼乽惓懱傪姶偠傞乿帠偑戝愗偱偡乯
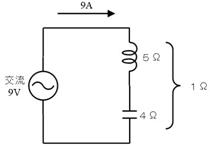
偙傟傑偱峫偊偰偒偨乽僀儞僺乕僟儞僗乮偺戝偒偝乯乿偩偗偱偼偙偺栤戣偼夝寛偱偒傑偣傫丅偙傟偐傜愢柧偡傞岎棳棟榑偼丄偙偺傛偆側晄巚媍側尰徾傪暘傝堈偔夝寛偡傞偨傔偺暘栰偱偡丅
傑偢丄岎棳棟榑偺婎杮偺峫偊曽傪丄捈棳棟榑偲斾妑偟偰愢柧偟傑偡丅捈棳棟榑偱偼壓恾嵍懁偺捠傝丄椺偊偽乽係兌乿偺傛偆偵丄侾偮偺抣偱乽棳傟擄偝乿傪昞偟傑偡丅偟偐偟丄岎棳棟榑偱偼摨偠乽棳傟擄偝乿傪丄壓恾塃懁偺捠傝乽塃偵係兌偱丄忋偵俁兌乿偺傛偆偵丄俀偮偺抣偱昞偟傑偡丅
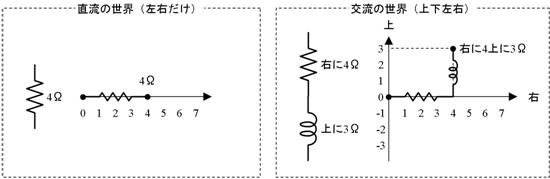
忋恾傪尒傟偽暘傞傛偆偵丄捈棳偱偼乽嵍塃乿乮捈慄乯偟偐柍偐偭偨悽奅偑丄岎棳偱偼乽忋壓偲嵍塃乿乮暯柺乯偵側傝傑偡丅偪傚偭偲傗傗偙偟偔側傝偦偆偱偡偑怱攝偼偁傝傑偣傫丅岎棳棟榑偺悽奅偼乮暯傜側柺偺忋偺榖側偺偱乯丄恾偵彂偄偰丄栚偱尒偰妋擣偱偒傑偡偐傜丄娙扨偵棟夝偱偒傑偡丅
|
岎棳棟榑偺摼堄暘栰
岎棳棟榑偼梊傔廃攇悢偑寛傑偭偰偄傞岎棳偑摼堄偱偡丅偨偲偊偽曻憲嬊偺揹攇傗丄僐儞僙儞僩偵撏偗傜傟傞揹椡偼廃攇悢偑寛傔傜傟偰偄偰丄戝偒偔曄傢傞偙偲偑偁傝傑偣傫偐傜丄岎棳棟榑偑摼堄側暘栰偱偡丅偝傜偵丄僆乕僨傿僆怣崋偺傛偆偵暋嶨側怣崋偱偁偭偰傕丄戲嶳偺岎棳偑崌傢偝偭偨傕偺偲峫偊偰丄岎棳棟榑傪墳梡偟偰埖偆偙偲偑偱偒傑偡丅媡偵岎棳偺嫮偝傗廃攇悢偑慺憗偔曄摦偡傞傛偆側夞楬偼丄岎棳棟榑偵偼嬯庤側暘栰偱偡丅
|
俁. 掞峈丄僐僀儖丄僐儞僨儞僒傪嬫暿偡傞
掞峈丄僐僀儖丄僐儞僨儞僒偺僀儞僺乕僟儞僗偼丄壗傟傕扨埵偑乽兌乿側偺偱丄堦尒摨偠暔偵尒偊傑偡丅偟偐偟晹昳偺庬椶偑堘偄傑偡偐傜丄偦傟偧傟暿偺惈幙偑偁傞敜偱偡丅偦偙偱丄曽岦偱嬫暿偟偰丄娫堘偊側偄傛偆偵岺晇偟傑偡丅
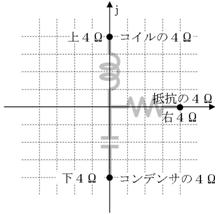
忋恾偺偲偍傝丄椺偊偽丄掞峈偼塃岦偒偵係兌丄僐僀儖偼忋岦偒偵係兌丄僐儞僨儞僒偼壓岦偒偵係兌偲曽岦晅偒偺僀儞僺乕僟儞僗偱昞尰偟傑偡丅
掞峈偺俀兌丄僐僀儖偺俁兌丄僐儞僨儞僒偺侾兌偺僀儞僺乕僟儞僗傪丄壓恾偺僌儔僼偵彂偒崬傫偱壓偝偄丅傑偨丄乽忋俆兌乿偺傛偆偵丄曽岦傪帵偟偰僀儞僺乕僟儞僗傪摎偊偰偔偩偝偄丅
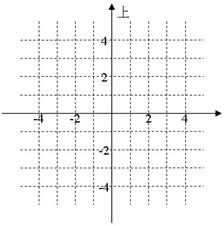
掞峈丂丂丂丂丂丂兌丄僐僀儖丂丂丂丂丂丂兌丄僐儞僨儞僒丂丂丂丂丂丂兌
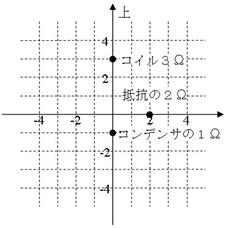
掞峈丂丂塃俀丂丂兌丄僐僀儖丂丂忋俁丂丂兌丄僐儞僨儞僒丂丂壓侾丂丂兌
係. 捈楍崌惉僀儞僺乕僟儞僗
壓恾嵍懁偺傛偆偵丄椺偊偽俁兌偲係兌偺掞峈傪捈楍偵宷偖偲丄俈兌偵側傝傑偟偨丅偲偙傠偑丄乮婛偵弎傋偨岎棳偺晄巚媍側尰徾偵傛偭偰乯壓恾塃懁偺傛偆偵丄僀儞僺乕僟儞僗俁兌偺僐僀儖偲係兌偺掞峈傪宷偄偱傕丄俈兌偵偼側傜偢丄俆兌偵側偭偰偟傑偄傑偡丅
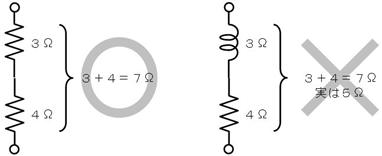
俈兌偲偄偆岆偭偨摎偑弌偨偺偼乽曽岦傪峫偊偢偵乿僀儞僺乕僟儞僗傪崌寁偟偨偐傜偱偡丅偮傑傝丄壓恾偺傛偆偵僀儞僺乕僟儞僗偺曽岦傪峫偊偰崌寁偡傞偲丄惓偟偔俆兌傪媮傔傞偙偲偑偱偒傑偡丅
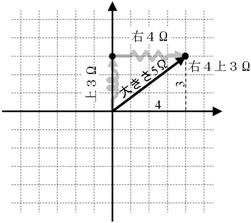
偮傑傝丄恾偺拞怱偐傜弌敪偟偰丄忋偵俁兌乮僐僀儖乯恑傒丄偝傜偵丄塃偵係兌乮掞峈乯恑傔偽丄嵟弶偺弌敪揰乮恾偺拞怱乯偐傜俆兌棧傟偨応強乮塃係偲忋俁乯偵摓拝偡傞丄偲峫偊傑偡丅
壓恾偺俀偮偺捈楍夞楬傪丄壓恾塃懁偺僌儔僼忋偱曽岦傪峫椂偟偰崌寁偟丄捈楍崌惉僀儞僺乕僟儞僗傪曽岦晅偒偱媮傔偰偔偩偝偄丅
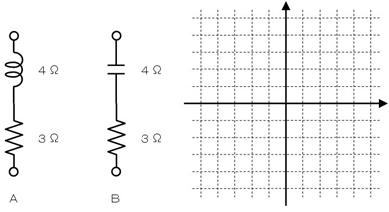
俙偺夞楬丗曽岦晅偒僀儞僺乕僟儞僗丂丂丂丂偲丂丂丂兌丄僀儞僺乕僟儞僗偺戝偒偝丂丂丂丂丂兌
俛偺夞楬丗曽岦晅偒僀儞僺乕僟儞僗丂丂丂丂偲丂丂丂兌丄僀儞僺乕僟儞僗偺戝偒偝丂丂丂丂丂兌
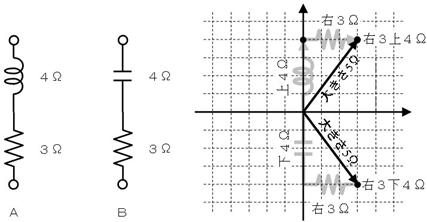
俙偺夞楬丗曽岦晅偒僀儞僺乕僟儞僗丂丂塃俁偲忋係丂兌丄僀儞僺乕僟儞僗偺戝偒偝丂丂丂俆丂兌
俛偺夞楬丗曽岦晅偒僀儞僺乕僟儞僗丂丂塃俁偲壓係丂兌丄僀儞僺乕僟儞僗偺戝偒偝丂丂丂俆丂兌
俆. 暋慺僀儞僺乕僟儞僗乮偁傞偄偼乽婼抺杺墹乿乯
乽暋慺僀儞僺乕僟儞僗乿偼岎棳棟榑偵椙偔弌偰偔傞乽幚偼娙扨側暼偵丄柤慜偩偗擄偟偄搝乿偱偡丅偨偲偊偽丄乽巕將乿偵乽婼抺杺墹乿偲柤慜傪晅偗傞偲丄柤慜偩偗暦偄偨恖偼乽嫲傠偟偄搝偵堘偄側偄乿偲岆夝偡傞偱偟傚偆丅
岎棳棟榑偑擄偟偔姶偠傜傟傞偺偼丄偙偺乽婼抺杺墹乿揑側僱乕儈儞僌偺搝傜偑挼椑骐缁偟偰偄傞忋偵丄偙偲傕偁傠偆偵乽婼抺杺墹乿偺柤偵憡墳偟偄丄杺奅僠僢僋側僆僪儘僆僪儘偟偄愢柧偑揥奐偝傟傞偐傜偱偡丅
|
椺偊偽丄乮倂倝倠倝倫倕倓倝倎傛傝乯

惓妋偱抁偄慺惏傜偟偄婰帠偱偡偑乧杮彂偺撉幰偵偼乽杺奅僠僢僋側僆僪儘僆僪儘僔僀愢柧乿偱偟傚偆丅偄偒側傝偙傟傪撉傫偩傜乽僼僃乕僓偼嫲傠偟偄搝偵堘偄側偄乿偲巚偆偺偼妋幚偱偡丅惓尫怣崋丄sin丄僆僀儔乕偺岞幃丄暋慺悢丄嫊悢扨埵丄愨懳抣丄曃妏丄嫊晹丄偲婼抺杺墹偺拠娫払傕挼椑骐缁偟偰偄傑偡丅杮彂偺乽岎棳夞楬乿傪撉傒廔偊傟偽丄忋偺愢柧偑壗傪尵偄偨偄偺偐帺慠偲暘傝傑偡丅
|
偦偙偱杮彂偱偼丄柤慜偼偦偺傑傑巊偄傑偡偑丄愢柧偼乽巕將偺偍榖乿偲偟偰丄擔忢僠僢僋偵愢柧偟傑偡丅乮柤慜傪偦偺傑傑巊偆偺偼丄懠恖偲夞楬偺榖傪偟偨帪偵丄捠偠傞曽偑妝偟偄偐傜偱偡乯
崱屻傕懡悢弌杤偡傞乽擄偟偦偆側柤慜偺搝乿偼慡偰乽柤慜偩偗擄偟偄搝乿偱偡丅偱偡偐傜乽傑偨婼抺杺墹偑弌偨偐乧偙偺巕將傔両乿偲巚偭偰僫儊偰妡偐偭偰偔偩偝偄丅
偝偰丄暋慺僀儞僺乕僟儞僗偼丄壓昞偺偲偍傝丄乽曽岦晅偒僀儞僺乕僟儞僗乿偺岦偒傪乽忋乿乽壓乿偲娍帤偱彂偔戙傢傝偵丄乽亄倞乿乽亅倞乿偲婰崋偱彂偄偨暔偱偡丅
|
曽岦晅偒僀儞僺乕僟儞僗昞偟曽
|
|
慺巕
|
掞峈
|
僐僀儖
|
僐儞僨儞僒
|
|
娍帤偱彂偔
|
塃係兌
|
忋係兌
|
壓係兌
|
|
婰崋偱彂偔
乮暋慺僀儞僺乕僟儞僗乯
|
亄係兌
|
亄倞係兌
|
亅倞係兌
|
埲忋偱偡丅
壓昞偺暋慺僀儞僺乕僟儞僗傪帩偮慺巕偑丄偦傟偧傟丄僐僀儖乮俴乯丄僐儞僨儞僒乮俠乯丄掞峈乮俼乯偺偳傟偱偁傞偐傪慖戰偟丄傑偨丄僀儞僺乕僟儞僗偺曽岦傪慖傫偱壓偝偄丅
|
暋慺僀儞僺乕僟儞僗
|
慺巕偺庬椶
|
僀儞僺乕僟儞僗偺曽岦
|
|
係丏俈兌
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
亅倞俇丏俉兌
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
亄倞俁丏俁兌
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
暋慺僀儞僺乕僟儞僗
|
慺巕偺庬椶
|
僀儞僺乕僟儞僗偺曽岦
|
|
係丏俈兌
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
亅倞俇丏俉兌
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
亄倞俁丏俁兌
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
俇. 俴俠偺暋慺傾僪儈僞儞僗
捈棳偺応崌偲摨條偵丄岎棳偺棳傟堈偝乮傾僪儈僞儞僗乯偼丄岎棳偺棳傟擄偝乮僀儞僺乕僟儞僗乯偺媡悢偱偡丅
椺偊偽壓昞偵帵偡偲偍傝丄忋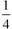 兌偺僐僀儖偺傾僪儈僞儞僗偼壓係俽偲側傝傑偡丅傑偨丄壓
兌偺僐僀儖偺傾僪儈僞儞僗偼壓係俽偲側傝傑偡丅傑偨丄壓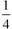 兌偺僐儞僨儞僒偺傾僪儈僞儞僗偼忋係俽偲側傝傑偡丅
兌偺僐儞僨儞僒偺傾僪儈僞儞僗偼忋係俽偲側傝傑偡丅
偙偺傛偆偵丄僀儞僺乕僟儞僗偼乽僐僀儖偑忋岦偒丄僐儞僨儞僒偑壓岦偒乿偱偟偨偑丄傾僪儈僞儞僗偼偦偺媡偲側傝乽僐僀儖偑壓岦偒丄僐儞僨儞僒偑忋岦偒乿偲側傝傑偡丅偙傟偼乽媡悢偵偡傞偲忋壓偑擖傟戙傢傞乿惈幙偑偁傞偐傜偱偡丅
|
柤慜
|
僀儞僺乕僟儞僗
|
|
傾僪儈僞儞僗
|
|
僀儊乕僕
|
岎棳偺棳傟擄偝
|
|
岎棳偺棳傟堈偝
|
|
僐僀儖
|
忋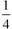 兌 傑偨偼 倞 兌 傑偨偼 倞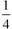 兌 兌
|
仼媡悢仺
|
壓係俽 傑偨偼 乕倞係俽
|
|
僐儞僨儞僒
|
壓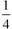 兌 傑偨偼 乕倞 兌 傑偨偼 乕倞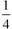 兌 兌
|
仼媡悢仺
|
忋係俽傑偨偼 倞係俽
|
偦傟偧傟係俽偺丄僐僀儖丄掞峈丄僐儞僨儞僒偺傾僪儈僞儞僗乮捠偟堈偝乯傪壓恾偵帵偟傑偡丅
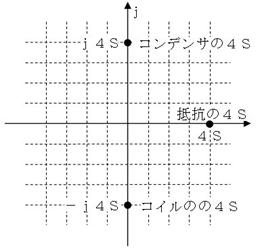
壓昞偺傾僪儈僞儞僗傪帩偮慺巕偑丄偦傟偧傟丄僐僀儖乮俴乯丄僐儞僨儞僒乮俠乯丄掞峈乮俼乯偺偳傟偱偁傞偐傪慖戰偟丄傑偨丄傾僪儈僞儞僗偺曽岦傪慖傫偱壓偝偄丅
|
暋慺傾僪儈僞儞僗
|
慺巕偺庬椶
|
傾僪儈僞儞僗偺曽岦
|
|
係丏俈俽
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
亅倞俇丏俉俽
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
亄倞俁丏俁俽
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
暋慺傾僪儈僞儞僗
|
慺巕偺庬椶
|
傾僪儈僞儞僗曽岦
|
|
係丏俈俽
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
亅倞俇丏俉俽
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
|
亄倞俁丏俁俽
|
俴丒俠丒俼
|
忋丒壓丒嵍丒塃
|
壓昞偵婰嵹偺奺慺巕偺丄暋慺僀儞僺乕僟儞僗偲暋慺傾僪儈僞儞僗傪婰擖偟丄曽岦傪慖傫偱偔偩偝偄丅
|
慺巕
|
侾侽兌偺掞峈
|
侾侽兌偺僐僀儖
|
侽丏侾兌偺僐儞僨儞僒
|
|
暋慺僀儞僺乕僟儞僗
|
丂丂丂丂丂兌
|
丂丂丂丂丂兌
|
丂丂丂丂丂兌
|
|
暋慺僀儞僺乕僟儞僗偺曽岦
|
忋丒壓丒嵍丒塃
|
忋丒壓丒嵍丒塃
|
忋丒壓丒嵍丒塃
|
|
暋慺傾僪儈僞儞僗
|
丂丂丂丂丂俽
|
丂丂丂丂丂俽
|
丂丂丂丂丂俽
|
|
暋慺傾僪儈僞儞僗偺曽岦
|
忋丒壓丒嵍丒塃
|
忋丒壓丒嵍丒塃
|
忋丒壓丒嵍丒塃
|
|
慺巕
|
侾侽兌偺掞峈
|
侾侽兌偺僐僀儖
|
侽丏侾兌偺僐儞僨儞僒
|
|
暋慺僀儞僺乕僟儞僗
|
丂丂丂侾侽兌
|
丂亄倞侾侽兌
|
亅倞侽丏侾兌
|
|
暋慺僀儞僺乕僟儞僗偺曽岦
|
忋丒壓丒嵍丒塃
|
忋丒壓丒嵍丒塃
|
忋丒壓丒嵍丒塃
|
|
暋慺傾僪儈僞儞僗
|
丂丂侽丏侾俽
|
亅倞侽丏侾俽
|
丂亄倞侾侽俽
|
|
暋慺傾僪儈僞儞僗偺曽岦
|
忋丒壓丒嵍丒塃
|
忋丒壓丒嵍丒塃
|
忋丒壓丒嵍丒塃
|
俈. 俴俠偺暋慺僀儞僺乕僟儞僗丒傾僪儈僞儞僗偺寁嶼
僐僀儖傗僐儞僨儞僒偺暋慺僀儞僺乕僟儞僗偼丄師昞偺傛偆偵寁嶼偱偒傑偡丅僀儞僺乕僟儞僗乮偺戝偒偝乯偺寁嶼偺慜偵丄倞傗亅倞傪晅偗偰丄曽岦傪昞偟偨偩偗偱偡丅
|
|
暋慺僀儞僺乕僟儞僗
|
暋慺傾僪儈僞儞僗
|
|
僐僀儖俴
|
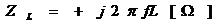
=COMPLEX(0,2*PI()*F1*L1)
|
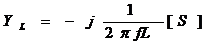
=COMPLEX(0,-1/2/PI()/F1/L1)
|
|
僐儞僨儞僒俠
|
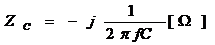
=COMPLEX(0,-1/2/PI()/F1/C1)
|
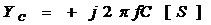
=COMPLEX(0,2*PI()*F1*C1)
|
椺偊偽丄倖亖俁侾俉俫倸丄俴亖侾侽倣俫乮侽丏侽侾俫乯偺応崌丄僐僀儖偺僀儞僺乕僟儞僗倅俴偼
倅俴亖倞俀兾倖俴亖倞亊俁丏侾係亊俁侾俉亊侽丏侽侾亖倞俀侽[兌]乮忋岦偒偺俀侽兌乯
侾倣俫偺僐僀儖偲丄侾侽侽兪俥偺僐儞僨儞僒偺暋慺僀儞僺乕僟儞僗傪媮傔偰丄壓恾偵彂偒崬傫偱偔偩偝偄丅偨偩偟丄廃攇悢偼俈俋俇俫倸偲偟傑偡丅
僐儞僨儞僒偺暋慺僀儞僺乕僟儞僗丂丂丂丂丂丂兌丄僐僀儖偺暋慺僀儞僺乕僟儞僗丂丂丂丂丂丂兌
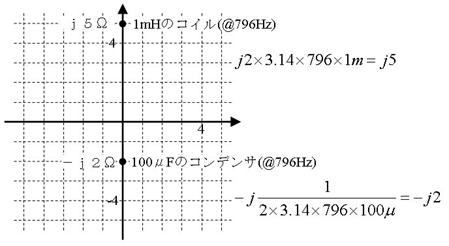
僐儞僨儞僒偺暋慺僀儞僺乕僟儞僗丂丂亅倞俀丂兌丄僐僀儖偺暋慺僀儞僺乕僟儞僗丂丂亄倞俆丂兌
俉. 俴俠俼捈楍夞楬
壓恾偺傛偆偵丄僐僀儖俴丄僐儞僨儞僒俠丄掞峈俼傪捈楍偵宷偄偩夞楬傪乽俴俠俼捈楍夞楬乿偲屇傃傑偡丅乮愙懕偺弴彉偑曄傢偭偰傕丄慡懱偺嶌梡偼摨偠偱偡乯偙偺椺偱偼丄俆兌偺僐僀儖丄係兌偺掞峈丄俀兌偺僐儞僨儞僒偑愙懕偝傟偰偄傑偡丅
偝偰丄夞楬慡懱偺僀儞僺乕僟儞僗傪媮傔傞偨傔偵丄掞峈偲摨條偵僀儞僺乕僟儞僗傪崌寁偡傞偲丄俆亄係亄俀亖侾侾兌偲側傝傑偡偑丄偙傟偼岆傝偱丄幚嵺偵偼俆兌偲側傝傑偡丅
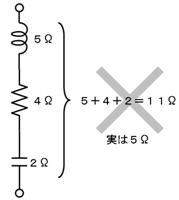
偙偺傛偆偵丄扨弮偵僀儞僺乕僟儞僗乮偺戝偒偝乯傪崌寁偟偰傕惓偟偄寢壥偑摼傜傟側偄偺偼乽僀儞僺乕僟儞僗偺曽岦乿傪峫偊偰偄側偐偭偨偐傜偱偟偨丅僀儞僺乕僟儞僗偺曽岦偼丄僐僀儖偼忋丄掞峈偼塃丄僐儞僨儞僒偼壓偱偟偨偐傜丄壓恾偺傛偆偵丄曽岦傪峫偊偰抧恾偺忋偱俁偮偺僀儞僺乕僟儞僗傪壛偊傑偡丅
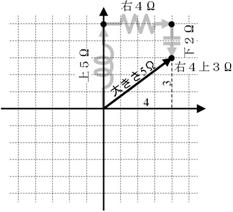
嵟弶偵僐僀儖偼忋偵俆兌側偺偱丄拞怱偐傜忋偵俆偮恑傒傑偡丅師偵丄掞峈偼塃偵係兌側偺偱丄塃偵係偮恑傒傑偡丄嵟屻偵丄僐儞僨儞僒偼壓偵俀兌側偺偱丄壓偵俀偮恑傒傑偡丅偙偺寢壥丄忋恾偵幬傔偺栴報偱帵偡僀儞僺乕僟儞僗乮塃偵係丄忋偵俁乯偑俴俠俼捈楍夞楬偺暋慺僀儞僺乕僟儞僗偵側傝傑偡丅
偦偺寢壥丄俴俠俼捈楍夞楬偺僀儞僺乕僟儞僗偺戝偒偝乮弌敪抧揰偐傜偳傟偩偗棧傟偨偐乯偼丄忋恾偺幬傔栴報偺挿偝乮俆兌乯偲側傝傑偡丅
恾傪昤偐偢偵峫偊傞偲偒偼丄忋壓傪峫椂偟偰乧
丂僐僀儖偲掞峈偲僐儞僨儞僒
亖忋俆兌偲塃係兌偲壓俀兌
亖塃係偲乮忋俆偲壓俀乯丂丂丂丂丂丂忋壓偑懪偪徚偟偁偭偰乧
亖塃係偲忋俁兌
偁傞偄偼乽忋乿乽壓乿偺曄傢傝偵乽亄倞乿乽亅倞乿傪巊偭偰乮暋慺僀儞僺乕僟儞僗偲偟偰乯寁嶼偡傞偙偲傕偱偒傑偡丅
丂僐僀儖亄掞峈亄僐儞僨儞僒
亖亄倞俆兌亄係兌亅倞俀兌
亖係亄乮亄倞俆亅倞俀乯丂丂丂丂丂丂亄倞偲乕倞偑懪偪徚偟偁偭偰乧
亖係亄倞俁兌
係偲俁偑媮傑傟偽丄師偺傛偆偵丄僺僞僑儔僗偺掕棟偱幬傔晹暘偺挿偝乮僀儞僺乕僟儞僗偺戝偒偝乯傪媮傔傞偙偲偑偱偒傑偡丅
俤倶們倕倢偱=SQRT(4^2+3^2)偲擖椡偟偰俆兌
暋慺僀儞僺乕僟儞僗傪巊偭偰偄傞偲偒偼丄師偺傛偆偵乽愨懳抣乿偲偄偆寁嶼乮俤倶們倕倢側傜IMABS娭悢乯偱娙扨偵戝偒偝傪媮傔傞偙偲偑偱偒傑偡丅
仸俤倶們倕倢偵偪傚偭偲偟偨愝掕偑昁梫偱偡乽俤倶們倕倢偱暋慺悢傪寁嶼偡傞乿傪偛棗壓偝偄
丂僀儞僺乕僟儞僗偺戝偒偝
亖暋慺僀儞僺乕僟儞僗偺愨懳抣
亖乥係亄倞俁乥
俤倶們倕倢偱=IMABS("4+3i")偲擖椡偟偰丄
亖俆兌
壓恾偺俴俠俼捈楍夞楬偺崌惉僀儞僺乕僟儞僗傪恾傪昤偄偰媮傔丄暋慺僀儞僺乕僟儞僗偲丄僀儞僺乕僟儞僗偺戝偒偝傪摎偊偰偔偩偝偄丅
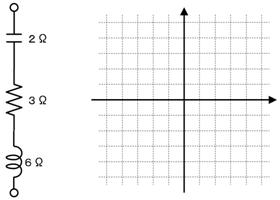
暋慺僀儞僺乕僟儞僗丂丂丂丂丂丂兌丄僀儞僺乕僟儞僗偺戝偒偝丂丂丂丂丂兌
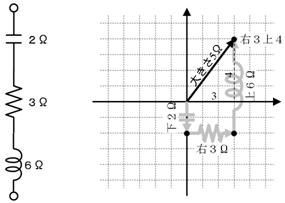
暋慺僀儞僺乕僟儞僗丂俁亄倞係丂兌丄僀儞僺乕僟儞僗偺戝偒偝丂丂俆丂丂兌
俋. 俴俠俼暲楍夞楬
壓恾偺傛偆偵丄僐僀儖俴丄僐儞僨儞僒俠丄掞峈俼傪暲楍偵宷偄偩夞楬傪乽俴俠俼暲楍夞楬乿偲屇傃傑偡丅乮愙懕偺埵抲偑曄傢偭偰傕丄慡懱偺嶌梡偼摨偠偱偡乯偙偺椺偱偼丄俆俽偺僐僀儖丄係俽偺掞峈丄俀俽偺僐儞僨儞僒偑愙懕偝傟偰偄傑偡丅乮暲楍側偺偱乽捠偟堈偝乿偱峫偊偰偄傑偡乯
偝偰丄夞楬慡懱偺傾僪儈僞儞僗乮岎棳偺捠傝傗偡偝乯傪媮傔傞偨傔偵丄掞峈偲摨條偵傾僪儈僞儞僗傪崌寁偡傞偲丄俆亄係亄俀亖侾侾俽偲側傝傑偡偑丄偙傟偼岆傝偱丄幚嵺偵偼俆俽偲側傝傑偡丅
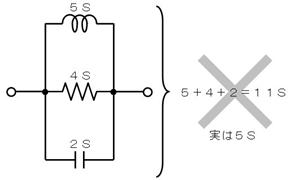
偙偺傛偆偵丄扨弮偵傾僪儈僞儞僗乮偺戝偒偝乯傪崌寁偟偰傕惓偟偄寢壥偑摼傜傟側偄偺偼乽傾僪儈僞儞僗偺曽岦乿傪峫偊偰偄側偐偭偨偐傜偱偟偨丅傾僪儈僞儞僗偺曽岦偼丄僐僀儖偼壓丄掞峈偼塃丄僐儞僨儞僒偼忋偱偟偨偐傜丄壓恾偺傛偆偵丄曽岦傪峫偊偰抧恾偺忋偱俁偮偺僀儞僺乕僟儞僗傪壛偊傑偡丅
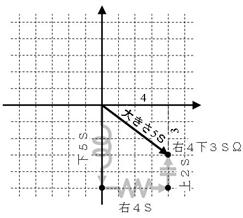
嵟弶偵僐僀儖偼壓偵俆俽側偺偱丄拞怱偐傜壓偵俆偮恑傒傑偡丅師偵丄掞峈偼塃偵係兌側偺偱丄塃偵係偮恑傒傑偡丄嵟屻偵丄僐儞僨儞僒偼忋偵俀俽側偺偱丄忋偵俀偮恑傒傑偡丅偙偺寢壥丄忋恾偵幬傔偺栴報偱帵偡傾僪儈僞儞僗乮塃偵係丄壓偵俁乯偑俴俠俼暲楍夞楬偺暋慺傾僪儈僞儞僗偵側傝傑偡丅
偦偺寢壥丄俴俠俼捈楍夞楬偺傾僪儈僞儞僗偺戝偒偝乮弌敪抧揰偐傜偳傟偩偗棧傟偨偐乯偼丄忋恾偺幬傔栴報偺挿偝乮俆俽乯偲側傝傑偡丅
恾傪昤偐偢偵峫偊傞偲偒偼丄忋壓傪峫椂偟偰乧
丂壓俆俽偲塃係俽偲忋俀俽
亖塃係偲壓俁俽
偁傞偄偼乽忋乿乽壓乿偺曄傢傝偵乽亄倞乿乽亅倞乿傪巊偭偰乮暋慺傾僪儈僞儞僗偲偟偰乯寁嶼偡傞偙偲傕偱偒傑偡丅
丂亅倞俆俽亄係俽亄倞俀俽
亖係亅倞俁俽
係偲俁偑媮傑傟偽丄師偺傛偆偵丄僺僞僑儔僗偺掕棟偱幬傔晹暘偺挿偝乮僀儞僺乕僟儞僗偺戝偒偝乯傪媮傔傞偙偲偑偱偒傑偡丅
俤倶們倕倢偱=SQRT(4*4+3*3)偲擖椡偟偰俆俽
暋慺傾僪儈僞儞僗傪巊偭偰偄傞偲偒偼丄師偺傛偆偵乽愨懳抣乿偲偄偆寁嶼乮俤倶們倕倢側傜IMABS娭悢乯偱娙扨偵戝偒偝傪媮傔傞偙偲偑偱偒傑偡丅
仸俤倶們倕倢偵偪傚偭偲偟偨愝掕偑昁梫偱偡乽俤倶們倕倢偱暋慺悢傪寁嶼偡傞乿傪偛棗壓偝偄
丂乥係亅倞俁乥
=IMABS("4-3i)
亖俆俽
慺巕偺抣偑傾僪儈僞儞僗乵俽乶偱偼側偔丄僀儞僺乕僟儞僗乵兌乶偱暘偭偰偄傞偲偒偼丄傑偢媡悢偵偟偰傾僪儈僞儞僗偵曄姺偟丄偦偺屻壛偊偰暲楍愙懕偟偨抣傪媮傔傑偡丅偙偺摎偼傾僪儈僞儞僗偱弌偰偒傑偡偐傜丄摎傪僀儞僺乕僟儞僗偱弌偡偲偒偼丄嵞搙媡悢偵偟傑偡丅
偮傑傝丄暲楍崌惉暋慺僀儞僺乕僟儞僗偺寁嶼偼丄暲楍崌惉掞峈偲摨偠偱丄
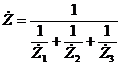
=IMDIV(1,IMSUM(IMDIV(1,Z1),IMDIV(1,Z2),(MDIV(1,Z3)))
偲寁嶼偟傑偡丅
侾侽. 僩儔儞僗
僩儔儞僗偼丄堦偮偺揝怱乮僐傾乯偵俀偮乮埲忋乯偺僐僀儖傪姫偄偨晹昳偱丄壓恾忋懁偺傛偆偵丄岦偐偄崌偭偨僐僀儖偺恾婰崋偱帵偟傑偡丅恾婰崋偺拞墰偺廲朹偼揝怱傪昞偟偰偄傑偡丅
偙偺傛偆偵丄恾婰崋偑僐僀儖偲帡偰偍傝丄峔憿傕僐僀儖偲摨偠偱偡偑乮摫慄傪姫偒晅偗偨晹昳偱偡偑乯丄僩儔儞僗偺摥偒偼僐僀儖偲偼傑傞偱堎側傝丄棟憐揑側僩儔儞僗偵偼僐僀儖惉暘乮僀儞僟僋僞儞僗乯偑偁傝傑偣傫丅
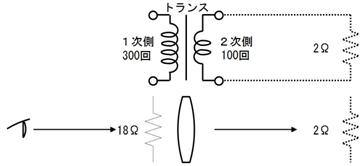
僩儔儞僗偼僀儞僺乕僟儞僗偺拵娽嬀偱偡丅椺偊偽忋恾偺僩儔儞僗偺俀師懁偵俀兌偺掞峈傪愙懕偡傟偽侾師懁偐傜偼丄傑傞偱侾俉兌偺掞峈偑愙懕偝傟偰偄傞傛偆偵尒偊傑偡丅偱偡偐傜丄侾師懁偵侾俉倁俙俠偺揹埑傪壛偊傞偲丄侾俙俙俠偺揹棳偑棳傟傑偡丅偙偺偲偒俀師懁偺俀兌偺掞峈偵偼丄俇倁俙俠偺揹埑偑壛傢傝丄俁俙俙俠偺揹棳偑棳傟偰偄傑偡丅
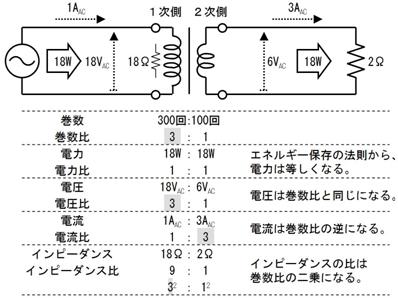
壓恾偼僩儔儞僗偺揹埑傗揹棳傪斾妑偟偨恾偱偡丅姫悢偑俁丗侾側傜丄揹埑傕俁丗侾偲側傝傑偡丅媡偵揹棳偼侾丗俁偲側傝傑偡丅偦偺寢壥丄擇師懁偵愙懕偝傟偨俀兌偺掞峈偼丄侾師懁偐傜偼乮侾俉倁俙俠偱侾俙俙俠偑棳傟傞偺偱乯侾俉兌偵丄偮傑傝丄俋攞乮姫悢斾俀亖俁俀亖俋攞乯偺僀儞僺乕僟儞僗偵尒偊傑偡丅
侾侽.侾. 楙廗
壓恾偼丄侾師懁俀侽侽夞偱俀師懁侾侽侽夞偺僩儔儞僗傪巊梡偟偨夞楬偱偡丅侾師懁偵偼俀兌偺掞峈傪捠偠偰侾侽倁俙俠偺揹埑傪愙懕偟丄俀師懁偵俀兌偺晧壸傪愙懕偟偰偄傑偡丅
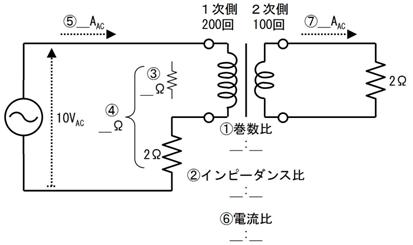
忋恾偺僩儔儞僗偺侾師懁偲俀師懁偵棳傟傞揹棳傪丄壓昞偵婰擖偟側偑傜媮傔偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
姫悢斾偼丄
|
丗
|
|
嘇
|
僀儞僺乕僟儞僗斾偼丄
乮姫悢斾偺擇忔偩偐傜丄乯
|
丗
|
|
嘊
|
俀師懁偵愙懕偝傟偨晧壸偺俀兌偼丄侾師懁偐傜偼壗兌偵尒偊傑偡偐丄
|
兌
|
|
嘋
|
侾師懁偺僀儞僺乕僟儞僗偺崌寁偼丄
|
兌
|
|
嘍
|
侾師懁偺揹棳偼丄
乮侾師懁偺揹埑偼侾侽倁俙俠偩偐傜丄乯
|
俙俙俠
|
|
嘐
|
揹棳斾偼丄
|
丗
|
|
嘑
|
俀師懁偺揹棳偼丄
|
俙俙俠
|
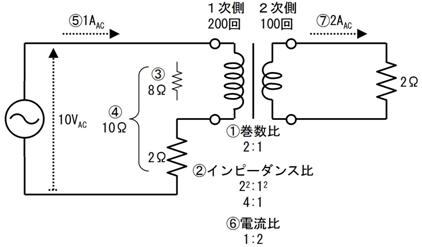
侾侽.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
姫悢斾偼丄
|
俀丗侾
|
|
嘇
|
僀儞僺乕僟儞僗斾偼丄
乮姫悢斾偺擇忔偩偐傜丄乯
|
係丗侾
|
|
嘊
|
俀師懁偵愙懕偝傟偨晧壸偺俀兌偼丄侾師懁偐傜偼壗兌偵尒偊傑偡偐丄
|
俉兌
|
|
嘋
|
侾師懁偺僀儞僺乕僟儞僗偺崌寁偼丄
|
侾侽兌
|
|
嘍
|
侾師懁偺揹棳偼丄
乮侾師懁偺揹埑偼侾侽倁俙俠偩偐傜丄乯
|
侾俙俙俠
|
|
嘐
|
揹棳斾偼丄
|
侾丗俀
|
|
嘑
|
俀師懁偺揹棳偼丄
|
俀俙俙俠
|
侾侾. 楻傟僀儞僟僋僞儞僗
壓恾乮倎乯偵帵偡偲偍傝丄棟憐揑側僩儔儞僗偱偼丄俀師懁偵掞峈傪愙懕偡傟偽丄侾師懁偐傜傕掞峈偵尒偊傑偡丅偟偐偟丄壓恾乮倐乯偺傛偆偵丄侾師懁姫慄偱敪惗偟偨帴婥乮帴懇乯偑慡偰俀師懁姫慄偺拞傪捠傜側偄応崌偼丄侾師懁偐傜尒傞偲僐僀儖偺惉暘乮僀儞僟僋僞儞僗乯偑惗偠傑偡丅
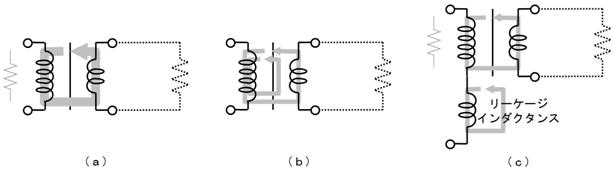
側偤側傜丄忋恾乮們乯偺傛偆偵丄乮侾師懁姫慄偱敪惗偟乯俀師懁姫慄傪捠偭偨帴懇偼僩儔儞僗偲偟偰摥偒傑偡偑丄捠傜側偐偭偨帴懇偼僐僀儖偲偟偰摥偔偐傜偱偡丅
帴懇偑俀師懁偺姫慄偵擖傜偢偵丄楻傟偨暘偑僐僀儖偺惉暘乮僀儞僟僋僞儞僗乯傪敪惗偝偣偨偺偱丄忋恾乮們乯偺僐僀儖惉暘傪乽楻傟僀儞僟僋僞儞僗乿偁傞偄偼乽儕乕働乕僕僀儞僟僋僞儞僗乿偲屇傃傑偡丅
柍愙揰媼揹偺侾師懁偲俀師懁偺傛偆偵丄帴懇偺戝晹暘偑俀師姫慄傪捠傜側偄応崌偼丄嬌傔偰戝偒側楻傟僀儞僟僋僞儞僗偑惗偠傑偡丅偦偺寢壥丄壓恾乮倎乯偵帵偡傛偆偵丄侾師懁姫慄偵揹埑傪壛偊偰傕嬐偐側揹棳偟偐棳傟傑偣傫丅偙偺傛偆側応崌丄壓恾乮倐乯偵帵偡傛偆偵丄儕乕働乕僕僀儞僟僋僞儞僗偲摨摍側乮僀儞僺乕僟儞僗偺戝偒偝傪帩偮乯僐儞僨儞僒傪捈棳偵愙懕偡傞偙偲偱丄儕乕働乕僕僀儞僟僋僞儞僗傪懪偪徚偟偰丄侾師姫慄偵揹棳傪棳偡偙偲偑偱偒傞傛偆偵側傝傑偡丅
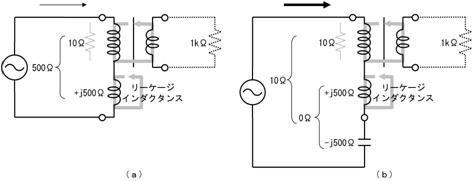
侾俀. 岎棳偲夞揮
偙偙傑偱丄僐僀儖傗僐儞僨儞僒偺僀儞僺乕僟儞僗傪岎棳棟榑揑偵乮暯柺忋偱乯峫偊偰棃傑偟偨丅偙偙偐傜偼丄揹棳傗揹埑傪岎棳棟榑揑偵乮暯柺忋偱乯峫偊偰傒傑偡丅
偝偰丄憱偭偰偄傞帺揮幵傪慜偐傜尒傞偲丄壓恾偺傛偆偵丄儁僟儖偑忋壓塣摦偟偰偄傞傛偆偵尒偊傑偡丅儁僟儖偺忋壓塣摦偼丄岎棳偲慡偔摨偠丄扨弮側曄壔傪孞傝曉偟傑偡丅
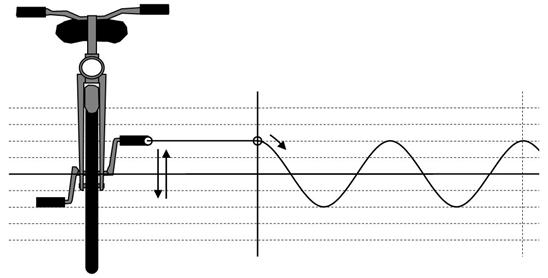
儁僟儖偺忋壓塣摦偼岎棳偲摨偠扨弮側曄壔
偲偙傠偱丄摨偠帺揮幵傪墶偐傜尒傞偲丄壓恾偺傛偆偵丄儁僟儖偼忋壓偟偰偄傞偺偱偼側偔丄幚偼夞揮偟偰偄傞帠偑暘傝傑偡丅
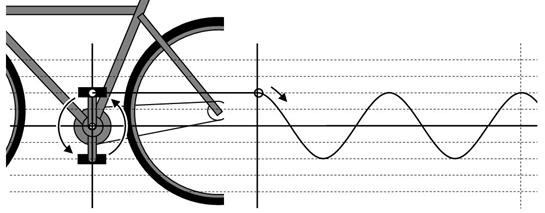
扨弮側曄壔偼儁僟儖偺夞揮偐傜惗傑傟傞
偮傑傝丄岎棳偺惓懱偼夞揮偱偡丅乮岎棳偺怳摦偼丄儁僟儖偺夞揮傪慜偐傜挱傔偨傕偺偱偡丅乯
偦傟偱偼丄乮岎棳偺惓懱偱偁傞乯儁僟儖偺夞揮傪條乆偵曄壔偝偣偰丄岎棳偑偳偺傛偆偵曄壔偡傞偐峫偊偰尒傑偟傚偆丅
偙偙偱偼壓恾偺傛偆偵丄儁僟儖偼帪寁偺俁帪偺埵抲偐傜僗僞乕僩偡傞帠偵偟傑偡丅儁僟儖偼嵟弶偵忋偑傝丄師偵壓偑傝傑偡丅偦偺寢壥岎棳偼丄壓恾塃懁偺攇傪昤偄偰忋壓偟傑偡丅
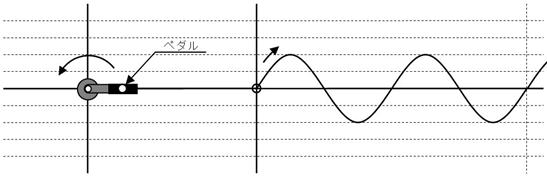
傑偢丄壓恾偺傛偆偵丄僋儔儞僋乮儁僟儖偺晅偄偰偄傞榬乯偑挿偄偲丄壓恾偺傛偆偵丄戝偒側岎棳偑惗傑傟傑偡丅
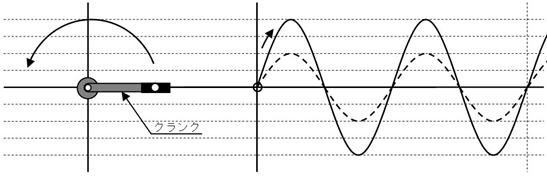
僋儔儞僋偺挿偝偲岎棳偺戝偒偝
傑偨丄壓恾偺傛偆偵丄儁僟儖傪憗偔夞偡偲丄廃攇悢偺崅偄岎棳偑惗傑傟傑偡丅
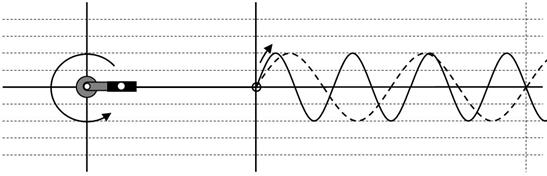
僋儔儞僋偺懍偝偲岎棳偺廃攇悢
偝傜偵丄壓恾偺傛偆偵丄儁僟儖偺嵟弶偺埵抲偑曄傢傞偲丄攇偑僘儗傑偡丅
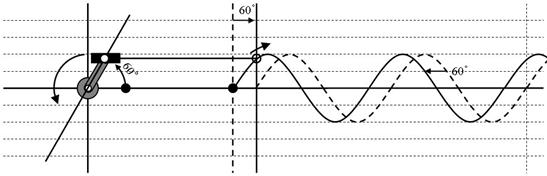
儁僟儖傪夞偡僞僀儈儞僌偲岎棳偺僘儗乮埵憡乯
儁僟儖偺嵟弶偵埵抲偑僉僢僠儕塃岦偒偺帪傪侽亱丄忋乮斀帪寁夞傝乯偵僘儗偨傜僾儔僗乮埵憡偑恑傫偱偄傞乯丄壓乮帪寁夞傝乯偵僘儗偨傜儅僀僫僗乮埵憡偑抶傟偰偄傞乯偲尵偄傑偡丅忋恾偺椺偱偼埵憡偑俇侽亱恑傫偱偄傑偡丅乽埵憡乿偲偼丄偙偙偱偼乽儁僟儖偺嵟弶偺妏搙乿偲偄偆堄枴偱偡丅
偙偺傛偆偵丄乽岎棳偼丄僋儔儞僋偺挿偝乮戝偒偝乯丄嵟弶偺埵抲乮埵憡乯丄夞偡憗偝乮廃攇悢乯偺俁偮偱昞偡帠偑偱偒傑偡乿丅偮傑傝丄忋恾嵍懁偺儁僟儖偺奊傪彂偄偰廃攇悢傪崘偘傟偽丄忋恾塃懁偺攇偺條巕傪彂偐側偔偰傕嵪傓傢偗偱偡丅偲偰傕妝偵側傞偺偱丄偙偺曽朄偑垽梡偝傟偰偄傑偡丅
壓恾壓懁偺岎棳偵懳墳偡傞儁僟儖偺嵟弶偺埵抲傪丄椺偵曧偭偰彂偒崬傫偱偔偩偝偄丅墌偺敿宎乮嵟戝揹埑乯偼壗儃儖僩偱偡偐丅侾昩偵傗偭偰棃傞攇偺夞悢乮廃攇悢乯偼壗僿儖僣偱偡偐丅
|
椺
|
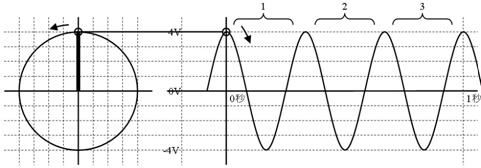
嵟戝揹埑乮僋儔儞僋偺敿宎乯係倁丂廃攇悢乮侾昩偵傗偭偰棃傞攇偺壓恾乯俁俫倸
|
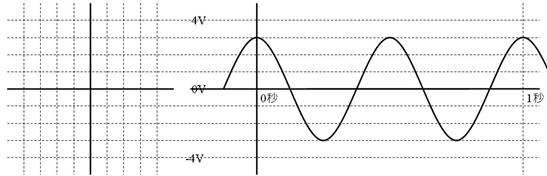
嵟戝揹埑乮僋儔儞僋偺敿宎乯丂丂丂倁丂廃攇悢乮侾昩偵傗偭偰棃傞攇偺壓恾乯丂丂丂俫倸
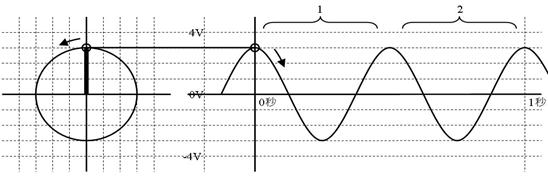
嵟戝揹埑乮僋儔儞僋偺敿宎乯丂俁丂倁丂廃攇悢乮侾昩偵傗偭偰棃傞攇偺壓恾乯丂俀丂俫倸
壓恾偺岎棳偵懳墳偡傞儁僟儖偺嵟弶偺埵抲傪丄彂偒崬傫偱偔偩偝偄丅儁僟儖偺嵟弶偺埵抲乮埵憡乯偼恀塃岦偒偒偐傜壗搙僘儗偰偄傑偡偐丅僘儗偼僾儔僗偱偡偐丄儅僀僫僗偱偡偐丄偦傟偼丄恑傫偱偄傑偡偐丄抶傟偰偄傑偡偐丅
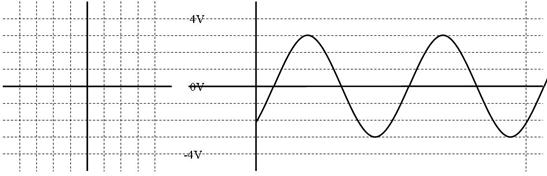
妏搙偺僘儗乮埵憡乯丂丂丂搙丄僾儔僗丒儅僀僫僗丄恑傫偱偄傞丒抶傟偰偄傞
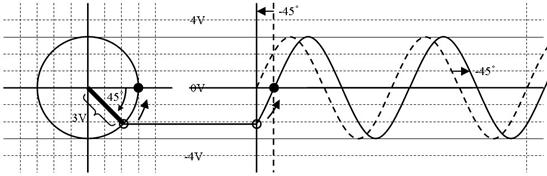
妏搙偺僘儗乮埵憡乯丂係俆搙丄儅僀僫僗丄抶傟偰偄傞
侾俁. 僼僃乕僓昞帵
乽僼僃乕僓昞帵乿傕丄乽柤慜偩偗擄偟偄搝乿偱偡丅僼僃乕僓昞帵偲偼丄壓恾嵍懁偵帵偡偲偍傝乮偙傟傑偱壗搙傕楙廗偟偨乯乽僋儔儞僋偺嵟弶偺埵抲乮壓恾嵍乯偱岎棳傪昞偟偨傕偺乿偱偡丅
僼僃乕僓偼恾偵昤偔偩偗偱偼側偔丄壓昞偺傛偆偵丄暥帤傪巊偭偰彂偔偙偲傕偱偒傑偡丅
僼僃乕僓偺彂偒曽
|
戝偒偝偲妏搙
|
嵍塃丄忋壓
|
塃傪亄丄忋傪亄倞
|
|
係丏俀係佢係俆亱
|
塃俁偲忋俁
|
亄俁丄亄倞俁
|
僼僃乕僓昞帵偼廃攇悢傪昞偟偰偄傑偣傫丅戝偒偝偲僘儗乮埵憡乯偩偗傪昞偟偰偄傑偡丅偦傟側偺偵丄岎棳偺妛栤乮岎棳棟榑乯偱偼椙偔巊傢傟傑偡丅偦偺棟桼偼丄椺偊偽丄僐儞僙儞僩偵嫙媼偝傟傞岎棳偑俆侽俫倸傗俇侽俫倸偱堦掕偱偁傞傛偆偵丄嵟弶偐傜廃攇悢偑寛傑偭偰偄傞応崌偑懡偔丄媡偺尵偄曽傪偡傟偽乽戝偒偝偲埵憡偩偗峫偊偨偄乿応崌偑懡偄偐傜偱偡丅
壓恾偺岎棳偺嵍懁偵丄儁僟儖偺嵟弶偺埵抲乮僼僃乕僓乯傪婰擖偟丄恾偺壓偵椺偊偽係佢係俆亱倁偺傛偆偵丄戝偒偝偲埵憡傪婰擖偟偰偔偩偝偄丅
僼僃乕僓偺戝偒偝偲埵憡丂丂丂丂丂丂丂丂倁
僼僃乕僓偺戝偒偝偲埵憡丂丂俁佢俋侽亱丂倁
壓恾偺嵍懁偵丄僼僃乕僓昞帵俀佢亅俇侽亱倁偺儁僟儖偺嵟弶偺埵抲傪婰擖偟丄壓恾塃懁偵偦偺夞揮偱惗偠傞攇宍傪婰擖偟偰偔偩偝偄丅偨偩偟丄廃攇悢偼俀俫倸偲偟傑偡丅
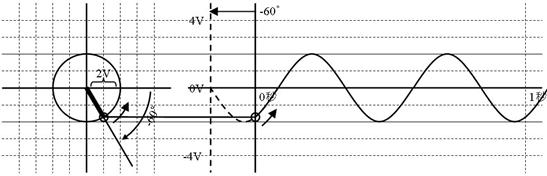
侾係. 僼僃乕僓偺惓懱
儁僟儖偑夞揮偡傞條巕傪丄壓恾偺傛偆偵昤偄偰棃傑偟偨丅
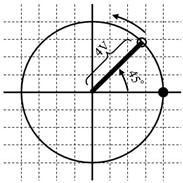
儁僟儖偑夞揮偡傞條巕
偲偙傠偑丄偙偺恾傪傕偭偲娙扨偵彂偔偙偲偑偱偒傑偡丅側偤側傜丄夞揮偡傞曽岦偼嵍夞傝偲寛傑偭偰偄傞偺偱丄夞揮曽岦偼晄梫丄偝傜偵丄昁偢墌傪昤偄偰夞揮偡傞偺偱丄夞揮傪昞偡墌偼晄梫丄偙偺傛偆偵晄梫側彂偒崬傒傪徣棯偡傞偲丄壓恾偺傛偆偵彂偔偙偲偑偱偒傑偡丅
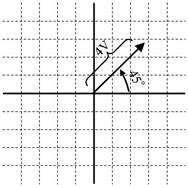
僼僃乕僓
偮傑傝丄戝偒偝偲埵憡乮嵟弶偺埵抲乯偺俀偮傪昞偡栴報傪堦偮彂偗偽岎棳傪昞偡偙偲偑偱偒傑偡丅偙偺栴報偑僼僃乕僓偺惓懱偱偡丅僼僃乕僓傪恾偵昤偗偽栴報偵側傝丄暥帤偱彂偗偽係佢係俆亱摍偲側傝傑偡丅
壓恾塃懁偵昤偐傟偨岎棳傪偺僼僃乕僓傪丄壓恾嵍懁偵栴報偱婰擖偟丄恾偺壓偵戝偒偝偲埵憡傪婰擖偟偰偔偩偝偄丅
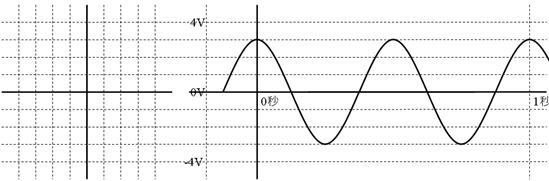
僼僃乕僓偺戝偒偝偲埵憡丂丂丂丂丂丂倁
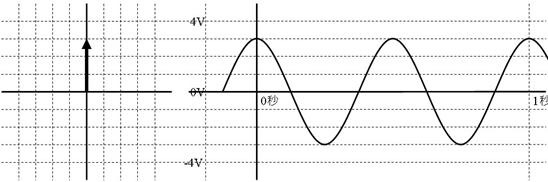
僼僃乕僓偺戝偒偝偲埵憡丂俁佢俋侽亱倁
壓恾塃懁偵昤偐傟偨岎棳偺僼僃乕僓傪丄壓恾嵍懁偵婰擖偟丄恾偺壓偵戝偒偝偲埵憡婰擖偟偰偔偩偝偄丅
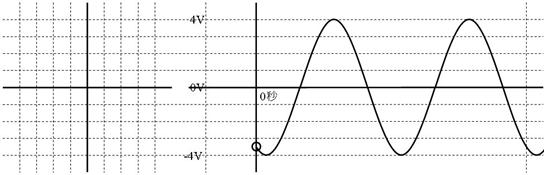
僼僃乕僓偺戝偒偝偲埵憡丂丂丂丂丂丂丂倁
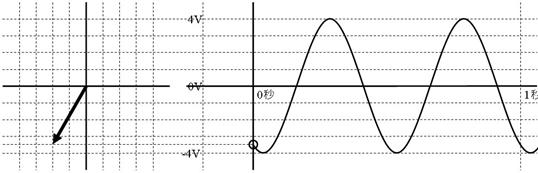
僼僃乕僓偺戝偒偝偲埵憡丂係佢乕侾俀侽亱倁
侾俆. 儔僕傾儞
擔忢惗妶偱偼丄妏搙傪椺偊偽乽俋侽亱乿摍偲乽搙乿偱昞偟傑偡丅偛懚抦偺捠傝丄堦廃偑俁俇侽亱偲寛傔傜傟偰偄傑偡丅偲偙傠偑俁俇侽偲尵偆抣偵偼戝偟偨崻嫆偑偁傝傑偣傫丅乮侾擭偑俁俇俆擔側偺偱丄侾擔偵抧媴偑栺侾亱岞揮偡傞丄偲偄偆掱搙偺棟桼偱俁俇侽偵寛傔偨傛偆偱偡乯偙偺傛偆偵丄崻嫆偺柍偄抣乮俁俇侽乯偑娷傑傟偰偄傞偲丄寁嶼偺僣僕僣儅偑崌傢側偔側傝傑偡丅壗偐丄傕偭偲崻嫆偺偼偭偒傝偟偨妏搙偺昞偟曽偑昁梫偱偡丅
傑偨丄妏搙傪應掕偡傞偵偼暘搙婍偑昁梫偱偡丅乽搙乿傪巊偆尷傝丄椺偊偽搚抧傪應検偡傞応崌乽姫広乿偲乽暘搙婍乿傪梡堄偡傞昁梫偑偁傝柺搢偱偡丅偦偙偱丄姫広偩偗偱妏搙傪應掕偱偒傞曽朄偑偁傟偽曋棙偱偡丅
偦偙偱姫広偩偗偱丄壓恾嵍懁偺搚抧傪應検偟偰傒傑偡丅偙偙偱偼丄嵍壓偺妏偺妏搙傪應傝傑偡丅傑偢丄壓恾塃懁偺傛偆偵丄姫広偺堦抂傪妏偺晹暘偵屌掕偟偰丄敿宎侾倣偺墌傪昤偒傑偡丅
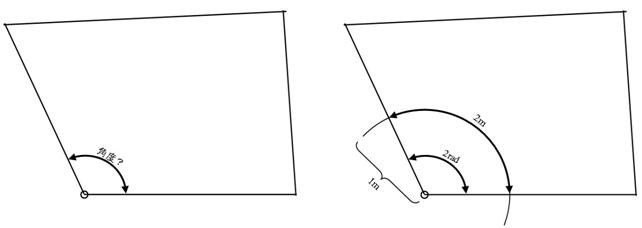
師偵丄妏搙傪媮傔偨偄晹暘偺墌屖偺挿偝傪姫広偱寁傝傑偡丅忋恾偺応崌墌屖偺挿偝偑乽俀倣乿偱偟偨丅偙傛偆側妏搙偑乽俀儔僕傾儞乿偱偡丅墌屖偑乽侾倣乿側傜乽侾儔僕傾儞乿丄乽俁倣乿側傜乽俁儔僕傾儞乿偱偡丅儔僕傾儞偼倰倎倓偲傕彂偒傑偡丅
偙偺傛偆偵姫広偩偗偱妏搙傪應掕偱偒傑偟偨丅偦偺偆偊丄儔僕傾儞偼乽敿宎侾倣偺墌屖偺挿偝乿偲偄偆柧妋側崻嫆偑偁傞偺偱丄寁嶼偱傕傄偭偨傝僣僕僣儅偑崌偄傑偡丅
偝偰丄俁俇侽亱傪儔僕傾儞偱昞偣偽丄敿宎侾倣偺墌偺墌廃偱偡偐傜丄俀兾儔僕傾儞偱偡丅偦偙偱丄埲壓帵偡傛偆偵丄搙偵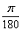 傪妡偗傟偽儔僕傾儞傪丄儔僕傾儞偵
傪妡偗傟偽儔僕傾儞傪丄儔僕傾儞偵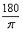 傪妡偗傟偽搙傪媮傔傞偙偲偑偱偒傑偡丅
傪妡偗傟偽搙傪媮傔傞偙偲偑偱偒傑偡丅
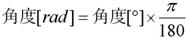 =D1*PI()/180
=D1*PI()/180
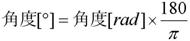 =D1*180/PI()
=D1*180/PI()
侾俇. 埵憡偲儔僕傾儞
壓恾偺岎棳偼丄戝偒偝偑係丄埵憡偑係俆亱恑傫偩岎棳揹埑偱偡丅係佢係俆亱倁偲彂偔偙偲偑偱偒傑偟偨丅
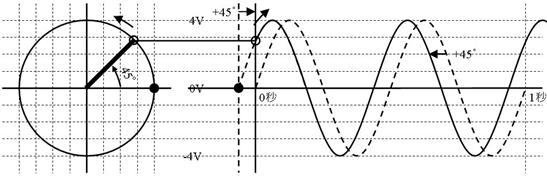
埵憡偺係俆亱偼丄儔僕傾儞傪巊偭偰丄侽丏俀俆兾 rad偲彂偔偙偲偑偱偒傑偡丅偟偨偑偭偰丄儔僕傾儞傪巊偭偰僼僃乕僓昞帵傪丄係佢侽丏俀俆rad倁偲彂偔偙偲傕偱偒傑偡丅
俁佢俀丏侽俋rad倁偺岎棳傪壓恾偵僼僃乕僓偱栴報昞帵偟偰偔偩偝偄丅
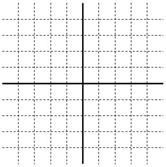
俀丏侽俋rad偼偩偄偨偄侾俀侽亱側偺偱丅
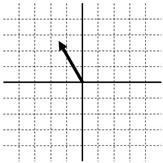
侾俈. 廃攇悢偲妏廃攇悢
廃攇悢偼侾昩娫偵棃偨攇偺壓恾傪悢偊偨傕偺偱偡偑丄妏廃攇悢偼侾昩娫偵儁僟儖偺夞揮偟偨妏搙傪乮儔僕傾儞偱乯應偭偨傕偺偱偡丅
傑偢丄壓恾偺岎棳偱丄侾昩娫偵儁僟儖偑壗夞揮偟偨偐悢偊偰偔偩偝偄丅
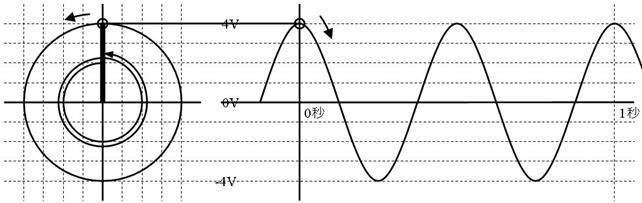
俀夞揮偟偰偄傑偡丅侾昩娫偵儁僟儖偑俀夞揮偟偨寢壥丄攇偑俀偮傗偭偰棃偨偙偲偑暘傝傑偡丅偮傑傝丄廃攇悢偺惓懱偼侾昩娫偺儁僟儖偺夞揮夞悢偱偡丅
夞揮傪乽夞悢乿偱偼側偔偰乽妏搙乿偱昞偡偙偲傕偱偒傑偡丅壓昞偵帵偡偲偍傝丄俀夞揮偱偡偐傜丄俁俇侽亱偺俀攞偱丄俈俀侽亱偱偡丅偙偺偨傔丄廃攇悢俀[俫倸]偼丄俈俀侽[亱/昩]偲昞偡偙偲傕偱偒傑偡丅偝傜偵丄妏搙傪儔僕傾儞偱帵偟偰丄係兾[rad/昩]乮侾俀丏俇[rad/昩]乯偲昞偡偙偲傕偱偒傑偡丅
|
廃攇悢
|
侾昩偺夞揮夞悢
|
侾昩偺夞揮妏搙乮搙乯
|
侾昩偺夞揮妏搙乮rad乯
|
|
俀俫倸
|
俀 夞揮乛昩
|
俈俀侽亱乛昩
|
侾俀丏俇 rad乛昩
(係兾rad乛昩乯
|
摿偵丄儔僕傾儞偱昞偟偨侾昩娫偺夞揮妏搙乮rad/昩乯傪巊偆偲丄寁嶼偑娙扨偵側傞偺偱丄乽妏廃攇悢乮冎乯乿偲屇傫偱垽梡偝傟偰偄傑偡丅
偝偰丄壗偲側偔僣僇儈僪僐儘偺柍偄乽妏廃攇悢乮冎乯乿偱偡偑丄暘偐傝堈偔僀儊乕僕偱偒傑偡丅偮傑傝壓恾偵帵偡偲偍傝丄妏廃攇悢乮冎乯偲偼乽挿偝侾倣偺儁僟儖偑丄侾昩娫偵恑傫偩嫍棧乮昤偄偨屖偺挿偝乯乿偱偡丅
椺偊偽3[rad/sec]偺応崌丄壓恾偺傛偆偵丄侾昩娫偵挿偝侾倣偺儁僟儖偑丄俁倣乮屖傪昤偄偰乯恑傓傛偆側夞揮偺懍偝乮偐傜惗傑傟傞忋壓摦偺廃攇悢乯丄偲峫偊傟偽椙偄栿偱偡丅
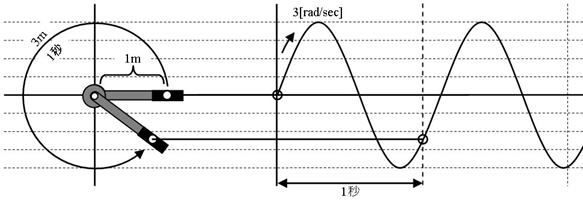
俁乵倰倎倓乛昩乶偺僀儊乕僕
寁嶼偟偰媮傔傞応崌偼丄廃攇悢[Hz]偵俀兾乮偮傑傝丄俇丏俀俉乯傪妡偗傞偲妏廃攇悢[rad/昩]偵丄妏廃攇悢[rad/昩]傪俀兾偱妱傞偲廃攇悢[Hz]偵側傝傑偡丅

壓恾偺岎棳偑侾昩娫偵夞揮偟偨條巕傪儁僟儖偺恾偵彂偒崬傒丄侾昩娫偵夞揮偟偨夞悢偲丄夞揮偟偨妏搙[d]傪媮傔偰偔偩偝偄丅
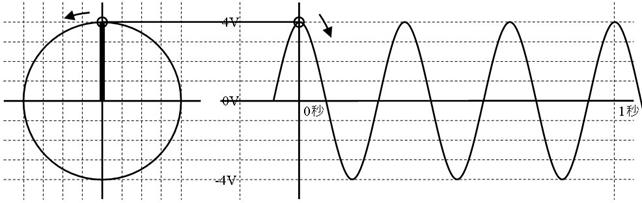
夞揮夞悢丂丂丂[Hz]丂夞揮妏搙丂丂丂丂[rad/昩]
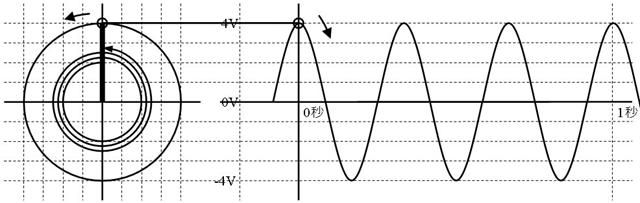
夞揮夞悢丂俁丂[Hz]丂夞揮妏搙侾俉丏俉[rad/昩]
侾俈.俁. 楙廗
壓昞忋抜偺廃攇悢偵懳墳偡傞妏廃攇悢傪丄壓抜偵婰擖偟偰偔偩偝偄丅
|
廃攇悢
|
0.16[Hz]
|
160[Hz]
|
16[kHz]
|
1.6[MHz]
|
|
妏廃攇悢
|
[rad/sec]
|
[k rad/sec]
|
[k rad/sec]
|
[M rad/sec]
|
侾俈.係. 摎
|
廃攇悢
|
0.16[Hz]
|
160[Hz]
|
16[kHz]
|
1.6[MHz]
|
|
妏廃攇悢
|
1[rad/sec]
=0.16/180*PI()
|
1 [k rad/sec]
=1000/180*PI()
|
100[k rad/sec]
=100E3/180*PI()
|
10[M rad/sec]
=10E6/180*PI()
|
侾俉. 妏廃攇悢偲俴俠偺僀儞僺乕僟儞僗
僐僀儖傗僐儞僨儞僒偺僀儞僺乕僟儞僗偺戝偒偝偼丄廃攇悢傪俫倸偱偼側偔丄妏廃攇悢rad乛sec偱昞偡偲丄壓昞偵帵偡偲偍傝丄幃偺拞偵偁偭偨乽俀兾乿偑柍偔側傝丄寁嶼偑娙扨偵側傝傑偡丅
妏廃攇悢偲僀儞僺乕僟儞僗
|
|
僀儞僺乕僟儞僗
|
傾僪儈僞儞僗
|
|
僐儞僨儞僒俠
|
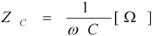
=1/O1/C1
|
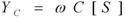
=O1*C1
|
|
僐僀儖俴
|
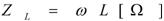
=O1*L1
|
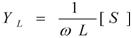
=1/O1/L1
|
椺偊偽丄倖亖俆侽rad/sec乮俁侾俉俫倸乯丄俴亖侾侽倣俫乮侽丏侽侾俫乯偺応崌丄僐僀儖偺僀儞僺乕僟儞僗倅俴偼
倅俴亖冎俴亖俆侽亊侽丏侽侾亖俀侽[兌]
=50*10E-3
偲寁嶼偟傑偡丅
僐僀儖傗僐儞僨儞僒偺暋慺僀儞僺乕僟儞僗傕丄妏廃攇悢傪巊偆偲壓昞偺傛偆偵娙扨偵側傝傑偡丅
|
|
暋慺僀儞僺乕僟儞僗
|
暋慺傾僪儈僞儞僗
|
|
僐僀儖俴
|
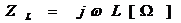
=IMAGINARY(0,O1*L1)
|
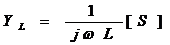
乮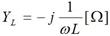 傪曄宍乯 傪曄宍乯
=IMDIV(1,IMAGINARY(0,O1*L1))
|
|
僐儞僨儞僒俠
|
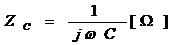
乮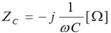 傪曄宍乯 傪曄宍乯
=IMDIV(1,IMAGINARY(0,O1*C1))
|
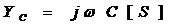
=IMAGINARY(0,O1*C1)
|
|
忋昞拞偺曄宍偼丄偨偲偊偽僐儞僨儞僒偺暋慺僀儞僺乕僟儞僗偺応崌丄
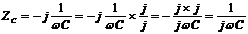
偺傛偆偵丄倞乛倞傪妡偗偰偐傜丄倞亊倞亖亅侾傪巊偭偰偄傑偡丅僐僀儖偺暋慺傾僪儈僞儞僗傕摨條偵曄宍偟偰偄傑偡丅
|
偙偙偱偼揹婥偺榖傪師偺僗僥僢僾偵恑傔傞偨傔丄偙傟傑偱婛偵巊偭偰偒偨暋慺悢傪寉偔暅廗偟偰丄俤倶們倕倢偱寁嶼偱偒傞傛偆偵偟丄偳偺傛偆側惈幙偑偁傞偐妋擣偟傑偡丅傕偪傠傫丄妛峑偺乽暋慺悢乿偲偼傑傞偱堘偄傑偡偐傜丄悢妛偑寵偄偱傕偛埨怱偔偩偝偄丅
僀儞僺乕僟儞僗偺崁偱巊偭偨傛偆偵丄乽暋慺悢乿偼娙扨偱曋棙側偺偵丄乮東栿偟偨恖偑乯擄偟偄柤慜傪晅偗偨偺偱丄僀儊乕僕偑埆偄偱偡丅偦偺偆偊丄乮俤倶們倕倢偱傗傟偽堦敪偩偲偄偆偺偵乯暋慺悢偺柺搢側庤寁嶼寁嶼傪妛峑偱嶶乆傗傜偝傟偰丄寵偄偵側偭偨恖傕懡偄偱偡丅杮彂偱偼俤倶們倕倢堦敪偱傗傝傑偡偐傜丄寁嶼偺昁梫偼杦偳偁傝傑偣傫丅乮倞亊倞亖亅侾偱偝偊丄柵懡偵巊偄傑偣傫偐傜偛埨怱傪乯
妛峑偱廗偭偨暋慺悢偑晛捠偵堸傒崬傔偰丄sin傗cos偲娭學偟偰偄偨帠傪偆偭偡傜妎偊偰偄傞丄俤倶們倕倢偱暋慺悢傪寁嶼偟偨妎偊傕偁傞丄偲偄偆曽偼杮復傪撉傓昁梫偼偁傝傑偣傫丅
偪傚偭偲嬅偭偨岎棳偺夞楬傗廃攇悢摿惈偺惓妋側寁嶼丄崅廃攇偺夞楬傪傗偭偰傒偨偄丄偲尵偆曽偵偼杮復偑昁梫偱偡丅媡偵丄捈棳傗娙扨側岎棳偺夞楬偟偐嶌傜側偄丄偲偄偆曽偵偼杮復偼昁梫偼偁傝傑偣傫丅
偲偼偄偊丄暋慺悢偲岎棳偼偆傑偄嬶崌偵宷偑偭偰偄傞偺偱丄暋慺悢傪棟夝偡傞偲岎棳偑椙偔暘偐傞傛偆偵側傝丄揹巕岺嶌傪堦憌妝偟傔傞傛偆偵側傝傑偡丅
杮復偼乽暋慺悢傪棟夝偡傞乿偺偱偼側偔偰乽暋慺悢偑巊偊傞傛偆偵側傞乿偙偲偩偗偵拲栚偟偰乮偮傑傝丄幚梡杮埵偵丄惓妋偝偼媇惖偵偟偰乯娙慺偵夝愢偟偰偄傑偡偐傜丄悢妛偱暋慺悢偺帪娫偑僀儎偩偭偨曽傕嬯捝柍偔撉傫偱捀偗傞撪梕偱偡丅乮媡偵丄傑偲傕偵暋慺悢傪棟夝偟偰偄傞曽偼乽側傔偲傫偐両乿偲暊傪棫偰傞偲巚偆乧偩偭偰丄巊偊偨傜偊偊傗傫丅乯
俀. 側偤暋慺悢偲屇傇偺偐
偝偰乽暋慺悢乿偼丄塸岅偱偼乽僐儞僾儗僢僋僗丒僫儞僶乕乿偲屇傃傑偡丅椺偊偽偍側偠傒偺乽僔僱儅丒僐儞僾儗僢僋僗乿偼乽塮夋娰乮僔僱儅乯偑偄偔偮偐僙僢僩偵側偭偨乮僐儞僾儗僢僋僗乯巤愝乿偱偡偑丄暋慺悢偼傕偭偲僔儞僾儖偱乽抣偑俀偮偩偗僙僢僩偵側偭偨悢乿偱偡丅偨偲偊偽丄係偲俁傪僙僢僩偵偡傟偽丄暋慺悢偑弌棃忋偑傝偱偡丅僔僱僐儞偲堘偭偰偨偭偨俀偮偩偗偺僙僢僩偱偡偐傜丄挻僔儞僾儖偱偡丅
|
乽僐儞僾儗僢僋僗乿傪乽暋慺乿偲丄乽僫儞僶乕乿傪乽悢乿偲柪栿偟偨偺偱偡偑丄偦偺寢壥偱偒偨乽暋慺悢乿偵偼乽慺悢乿乮俀丄俁丄俆丄俈丄丄丄乯偲偄偆丄暋慺悢偲偼娭學偺柍偄扨岅偑堦晹娷傑傟偰偟傑偄丄梋寁偵擄偟偔姶偠偰偟傑偄傑偡丅
|
偝偰丄悢帤傪俀偮僙僢僩偵偡傞偲丄応強傪昞偡偙偲偑偱偒傑偡丅偨偲偊偽丄壓偺抧恾偺傛偆偵乽擖傝岥偐傜丄塃偵係丄忋偵俁乿偲尵偆傛偆偵丄乽係乿偲乽俁乿偲偄偆俀偮偺悢帤偺僙僢僩偱丄偁側偨偑岞墍偵杽傔偨丄曮偺応強傪帵偡偙偲偑偱偒傑偡丅
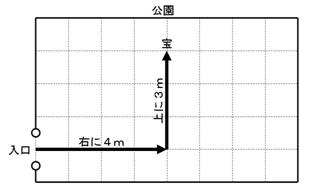
旈枾偺抧恾
偟偐偟丄乽塃偵係丄忋偵俁乿偲娍帤傪巊偭偰偄偰偼丄寁嶼偡傞偲偒偵柺搢偱偡丅偦偙偱丄乮僀儞僺乕僟儞僗偺強偱弌偰偒偨傛偆偵乯師偺昞偺傛偆偵娍帤傪傛傝娙扨側婰崋偵抲偒姺偊傑偡丅
娍帤傪婰崋偵抲偒姺偊傞
|
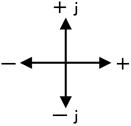
|
塃
伀
亄
|
嵍
伀
亅
|
忋
伀
亄倞
|
壓
伀
亅倞
|
偮傑傝塃嵍傪惓晧偺曽岦丄忋壓傪倞偺惓晧偺曽岦丄偲寛傔偨栿偱偡丅偙偆偡傟偽丄乽塃偵係丄忋偵俁乿偼丄乽亄係丄亄倞俁乿偲彂偔偙偲偑偱偒傑偡丅
偁偲偼丄俀偮偺悢乽亄係乿偲乽亄倞俁乿傪懌偟偰堦偮偵傑偲傔傞偲丄乽係亄倞俁乿偲偄偆暋慺悢偑姰惉偱偡丅偙偆偡傟偽丄壓恾偺傛偆偵丄乽係亄倞俁乿偲偄偆侾偮偺暋慺悢偱丄曮偺応強傪帵偡偙偲偑偱偒傑偡丅
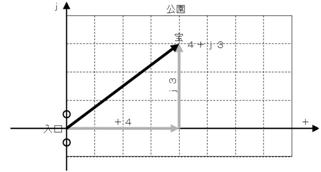
暋慺悢乽係亄倞俁乿偼乽侾偮偺悢乿側偺偵丄忋恾偵懢偄幬傔偺栴報偱帵偡傛偆側丄曮偺応強傪堦敪偱昞偡偙偲偑偱偒傞僗僌儗儌僲偱偡丅
俁. 幚晹偲嫊晹
暋慺悢偵娷傑傟傞俀偮偺抣偼丄偦傟偧傟偵柤慜傪晅偗偰嬫暿偟偰偄傑偡丅偨偲偊偽乽係亄倞俁乿偵娷傑傟傞乽係乿傪乽幚偺晹暘乿乮幚晹乯丄乽俁乿傪乽嫊偺晹暘乿乮嫊晹乯偲屇傃傑偡丅偮傑傝丄倞偺晅偄偰偄傞曽偑嫊晹偱偡丅
係. 俤倶們倕倢偱暋慺悢傪寁嶼偡傞
俤倶們倕倢偼摿暿側僆僾僔儑儞傪峸擖偡傞偙偲側偔丄娙扨側愝掕傪堦搙峴側偆偩偗偱丄暋慺悢傪寁嶼偡傞偙偲偑偱偒傑偡丅
俆. 俤倶們倕倢偺愝掕
師偺愝掕傪峴偊偽丄埲屻偼暋慺悢偑棙梡偱偒傑偡丅傑偢丄俤倶們倕倢傪棫偪忋偘偰丄儊僯儏乕僶乕偺乽僣乕儖乿偐傜乽傾僪僀儞乿傪慖戰偟傑偡丅
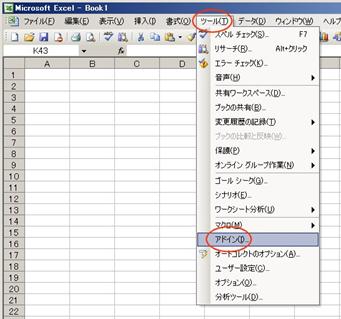
乽傾僪僀儞乿僟僀傾儘僌儃僢僋僗偑昞帵偝傟傑偡偐傜丄乽暘愅僣乕儖乿僠僃僢僋儃僢僋僗傪俷俶偵偟偰丄乽俷俲乿儃僞儞傪僋儕僢僋偟傑偡丅
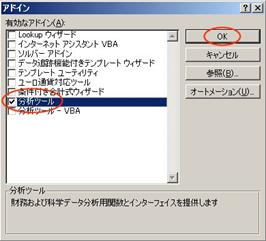
愝掕偼姰椆偱偡丅
俇. 俤倶們倕倢偵傛傞暋慺悢偺寁嶼
壓昞偺娭悢傪巊偭偰丄暋慺悢傪寁嶼偟傑偡丅庡偵IM乣偲偄偆偺偑暋慺悢娭楢偺娭悢偱偡丅
|
寁嶼
|
娭悢偺椺
屇傃曽
|
摦嶌偺椺
|
寢壥
|
|
暋慺悢傪擖椡
|
4+3i
|
暋慺悢4+j3傪嶌傞乮擖椡偡傞乯
|
4+3i
|
|
暋慺悢傪嶌傞
|
=COMPLEX(4,3)
僐儞僾儗僢僋僗
|
暋慺悢4+j3傪嶌傞
|
4+3i
|
|
懌偟嶼乮亄乯
|
=IMSUM ("4+3i","3+4i")
傾僀僄儉丒僒儉
|
暋慺悢4+j3偲3+j4傪偨偡
|
7+7i
|
|
堷偒嶼乮亅乯
|
=IMSUB ("4+3i","3+4i")
傾僀僄儉丒僒僽僩儔僋僩
|
暋慺悢4+j3偐傜3+j4傪堷偔
|
1-1i
|
|
妡偗嶼乮亊乯
|
=IMPRODUCT ("4+3i","3+4i")
傾僀僄儉丒僾儘僟僋僩
|
暋慺悢4+j3偲3+j4傪妡偗傞
|
25i
|
|
妱傝嶼乮亐乯
|
=IMDIV ("4+3i","3+4i")
傾僀僄儉丒僨傿價僕儑儞
|
暋慺悢4+j3傪3+j4偱妱傞
|
0.96-0.28i
|
|
幚晹傪庢傝弌偡
|
=IMREAL("4+3i")
傾僀僄儉丒儕傾儖
|
暋慺悢4+j3偺幚晹傪媮傔傞
|
4
|
|
嫊晹傪庢傝弌偡
|
=IMAGINARY("4+3i")
僀儅僕僫儕乕
|
暋慺悢4+j3偺嫊晹傪媮傔傞
|
3
|
|
愨懳抣
乮戝偒偝乯
|
=IMABS("4+3i")
傾僀僄儉丒傾僽僜儕儏乕僩
|
暋慺悢4+j3偺愨懳抣乮戝偒偝乯傪媮傔傞
|
5
|
|
曃妏
乮妏搙丄僘儗乯
|
=IMARGUMENT("4+3i")
傾僀僄儉丒僆乕僊儏儊儞僩
|
暋慺悢4+j3偺曃妏乮僘儗丄埵憡乯傪媮傔傞丂乮摎偺扨埵偼rad乯
|
0.643...
|
|
嫟栶
|
=IMCONJUGATE("4+3i")
傾僀僄儉丒僐儞僕儏僎乕僩
|
嫟栶側乮嫊晹偺晞崋偑媡偺乯暋慺悢傪媮傔傞
|
4-3i
|
|
exp娭悢
|
=IMEXP("4+3i")
僄僀僄儉丒僄僋僗億乕僱儞僔儍儖
|
e偺4+j3忔傪寁嶼偡傞
|
-54.05+7.704i
|
俤倶們倕倢偱偼丄暋慺悢乽倞俁乿偼丄乽俁倝乿偲昞帵偝傟傑偡乮擖椡偟傑偡乯丅偙傟偼悢妛偺彂偒曽乮俁倝乯偺曽偑丄揹婥偺彂偒曽乮倞俁乯傛傝椙偔巊傢傟傞偐傜偱偡丅
傑偨丄俤倶們倕倢偱偼暋慺悢偼乽暥帤楍乿偲偟偰僙儖偵擖傝傑偡丅偙偺偨傔娭悢偺妵屖偺拞偵捈愙婰擖偡傞応崌偼丄乭係亄俁倝乭偺傛偆偵丄乽
乭 乿乮僟僽儖僋僅乕僥乕僔儑儞乯偱埻傒傑偡丅
壓恾偺傛偆偵丄俛侾僙儖偵係亄倞俁丄俠侾僙儖偵俁亄倞係傪擖椡偟丄偦傟偧傟偺丄幚晹丄嫊晹丄愨懳抣丄曃妏丄俤倃俹娭悢抣丄傑偨丄憃曽偺榓丄嵎丄愊丄彍丄傪寁嶼偝偣偰偔偩偝偄丅
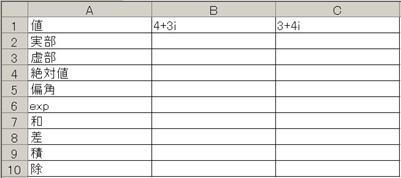
嵟弶偺侾夞栚偩偗偼丄僣乕儖偺傾僪僀儞偱暘愅傪俷俶偵偟傑偡丅乮俀夞栚偐傜偼晄梫偱偡乯僙儖偵師偺傛偆偵擖椡偟傑偡丅
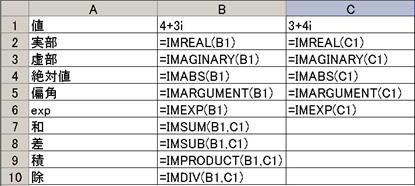
寢壥偼師偺傛偆偵昞帵偝傟傑偡丅
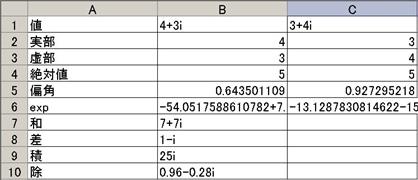
俈. 暋慺暯柺
壓恾偺岞墍偺抧恾傗丄帺揮幵偺儁僟儖傪墶偐傜尒偨恾偺傛偆側丄乽塃嵍偑惓晧偱丄忋壓偑倞偺惓晧乿傪昞偡恾乮僌儔僼乯傪乽暋慺暯柺乿偲屇傃傑偡丅

椺偵曧偭偰丄壓昞偺暋慺悢傪丄壓恾偺抧恾乮暋慺暯柺乯偵彂偒崬傫偱壓偝偄丅
|
椺丗係亄倞俁
|
俀亄倞侾
|
亅係亄倞俀
|
侾亅倞侾
|
亅係亅倞俁
|
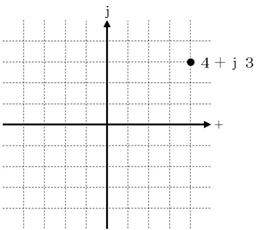
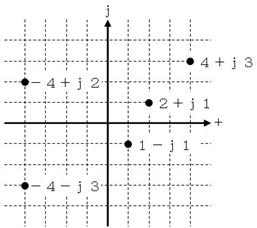
俉. 暋慺悢偺戝偒偝乮愨懳抣乯偲曃妏乮妏搙乯
崱堦搙丄曮偺抧恾傪尒偰傒傑偟傚偆丅
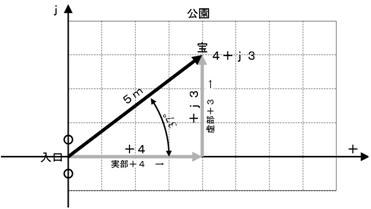
忋恾偵帵偡偲偍傝丄塃偵係倣丄忋偵俁倣恑傫偩曮偺偁傝偐偼丄暋慺悢偱係亄倞俁偲昞偡偙偲偑偱偒傑偟偨丅偙偺偲偒丄擖傝岥偐傜曮傑偱偺嫍棧偼俆倣偱偡丅偙偺俆倣傪乽暋慺悢偺戝偒偝乿傗乽愨懳抣乿偲屇傫偱丄俀杮偺廲朹偱埻傫偱帵偟傑偡丅偨偲偊偽丄係亄倞俁偺愨懳抣偼丄師偺傛偆偵彂偒傑偡丅乮僀儞僺乕僟儞僗偺崁偱傕怗傟傑偟偨乯
| 4+j3 | = 5
忋偺幃偼乽塃偵係丄忋偵俁恑傫偩曮偺埵抲偼丄擖傝岥偐傜俆倣偺嫍棧偵偁傞乿偲偄偆堄枴偱偡丅暋慺悢偺愨懳抣偼乽僺僞僑儔僗偺掕棟乿傪巊偭偰丄師偺傛偆偵寁嶼偱偒傑偡丅
| 4 + j3 | =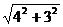 = 5丂丂丂乮暋慺悢(4 + j3)偺愨懳抣偼丄5乯
= 5丂丂丂乮暋慺悢(4 + j3)偺愨懳抣偼丄5乯
=IMABS("4+3i")
傑偨忋恾偱偼丄擖傝岥偐傜栺俁俈亱偺妏搙偵曮偑偁傝傑偡丅偙偺妏搙傪乽曃妏乿偲屇傃傑偡丅椺偊偽丄係亄倞俁偺曃妏偼丄倎倲倎値乮俁亐係乯偱寁嶼偱偒傑偡偑丄偙偺曽朄偼杮彂偱偼昁梫偁傝傑偣傫丅側偤側傜丄俤倶們倕倢傪巊偭偰丄俬俵俙俼俧倀俵俤俶俿乮乭係亄俁倝乭乯偲暋慺悢偐傜堦敪偱寁嶼偱偒傞偐傜偱偡丅
椺乮係亄倞俁乯偵側傜偭偰丄暋慺悢俇亄倞俉傪暋慺暯柺忋偵帵偟丄俤倶們倕倢傪梡偄偰丄幚晹丄嫊晹傪丄愨懳抣傪媮傔偰偔偩偝偄丅
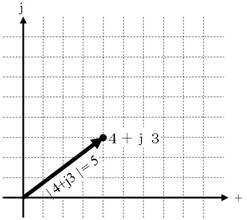
幚晹丗丂丂丂丂嫊晹丗丂丂丂丂愨懳抣丗丂丂丂丂曃妏丗丂丂丂丂丂丂亱
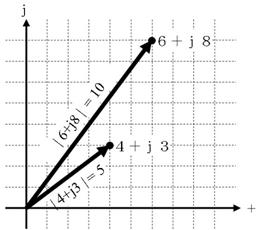
幚晹丗丂俇丂丂嫊晹丗丂俉丂丂愨懳抣丗丂侾侽丂曃妏丗俆俁丏侾丂亱
=IMREAL("6+8i")丄=IMAGINARY("6+8i")丄=IMABS("6+8i")丄=IMARGUMENT("6+8i")/PI()*180
仸曃妏偼儔僕傾儞偱摎偑偱傞偺偱丄侾俉侽乛兾傪妡偗傑偡丅
俋. 暋慺悢偺懌偟嶼
搻孈傪杊偖偨傔偵曮傪堏摦偝偣傑偟傚偆丅壓恾偵帵偡傛偆偵丄尰嵼偺応強偐傜丄塃偵俁丄壓偵俀恑傫偩応強偵杽傔捈偟傑偡丅塃偵俁丄壓偵俀偱偡偐傜丄俁亅倞俀偩偗堏摦偝偣偨帠偵側傝傑偡丅
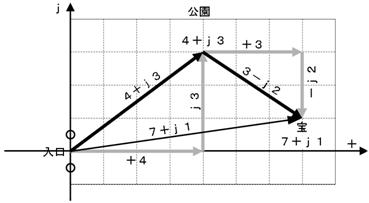
堏摦偝偣偨寢壥丄曮偼塃偵俈丄忋偵侾偺応強乮俈亄倞侾乯偵塀偝傟偰偄傑偡丅偙偺傛偆偵堦搙寛傔偨応強偐傜丄偝傜偵堏摦偝偣偨応強傪媮傔傞帠偑丄暋慺悢偺懌偟嶼偱偡丅偮傑傝丄
嵟弶偺応強 + 堏摦偟偨暘 = 4+j3 + 3-j2 = (4+3) + (3-2)j = 7 + j1
偺傛偆偵丄幚晹偲幚晹丄嫊晹偲嫊晹傪壛偊傞偩偗偱偡丅
侾侽. 暋慺悢偺妡偗嶼
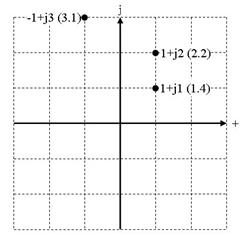
侾亄侾倞偲侾亄俀倞傪妡偗傞偲丄寢壥偼亅侾亄倞俁偲側傝傑偡丅偮傑傝丄
(1+ j 1) 亊 (1+ j 2) = -1+ j 3
=IMPRODUCT("1+1i","1+2i")
偲側傝傑偡丅偙偺寁嶼傪丄暋慺暯柺忋偵彂偔偲壓恾偺捠傝偱偡丅
妡偗嶼偺尦偵側偭偨俀偮偺悢乮侾亄侾倞偲侾亄俀倞乯偲丄妡偗嶼偺寢壥摼傜傟偨悢乮亅侾亄倞俁乯偺応強偵偼丄壗偺柆棈傕柍偄傛偆偵尒偊傑偡丅偦偙偱丄妏搙傗戝偒偝乮愨懳抣乯偵拲栚偡傞偲丄摿挜偑偁傝傑偡丅
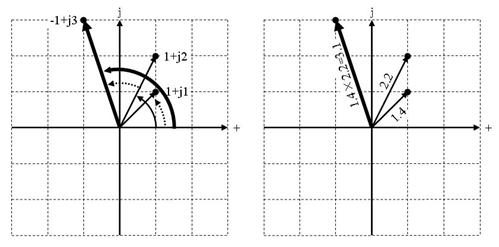
忋恾偺捠傝丄尦偵側偭偨俀偮偺悢偺妏搙乮曃妏乯傪壛偊偨傕偺偑丄妡偗嶼偱摼傜傟偨悢偺妏搙偲側傝丄傑偨丄尦偵側偭偨俀偮偺悢偺戝偒偝乮愨懳抣乯傪偐偗偨傕偺偑丄妡偗嶼偱摼傜傟偨悢偺戝偒偝偲側偭偰偄傑偡丅偮傑傝暋慺悢偺妡偗嶼偼丄妏搙偺偨偟嶼丄戝偒偝偺妡偗嶼丄偱偡丅
|
暋慺悢偺寁嶼偼俤倶們倕倢偑傗傝傑偡偐傜丄庤寁嶼偡傞昁梫偼偁傝傑偣傫丅嶲峫傑偱偵偦偺曽朄偼乮暘攝偺朄懃偲偄偆搝傪巊偭偰乧乯
丂丂丂 丂乮倎亄倞倐乯亊乮們亄倞倓乯
丂丂丂丂亖倎亊們亄倎亊倞倓亄倞倐亊們亄倞倐亊倞倓
丂丂丂丂亖倎亊們亅倐亊倓 亄 倞乮倎亊倓亄倐亊們乯
偲側傝傑偡丅乮倞亊倞亖亅侾偱偡乯
|
侾侾. 暋慺悢偺媡悢
暋慺悢偺媡悢偼丄戝偒偝乮愨懳抣乯偲曃妏乮妏搙乯偱彂偔偲暘傝堈偔丄椺偊偽師昞偺傛偆偵側傝傑偡丅
|
|
椺侾
|
椺俀
|
|
|
尦偺抣
|
媡悢
|
尦偺抣
|
媡悢
|
|
暋慺悢
|
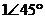
|
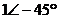
|
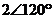
|
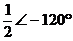
|
|
愨懳抣
|
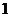
|
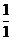
|
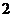
|
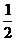
|
|
曃妏
|
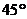
|
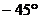
|
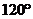
|
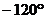
|
忋恾偺椺俀偱暘傞傛偆偵丄暋慺悢偺媡悢偱偼丄乽愨懳抣偑媡悢乿偵側傝乮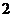 側傜
側傜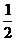 偵側傝乯丄乽曃妏偼晞崋偑媡乿乮120亱側傜-120亱乯偵側傝傑偡丅
偵側傝乯丄乽曃妏偼晞崋偑媡乿乮120亱側傜-120亱乯偵側傝傑偡丅
壓恾偺暋慺暯柺忋偵丄忋昞偺俀偮偺椺傪帵偟傑偡丅尦偺悢偲媡悢偼悈暯慄乮幚幉乯偲偺妏搙偼摨偠偱偡偑丄忋壓偑媡偵側傝傑偡丅
僀儞僺乕僟儞僗偲傾僪儈僞儞僗偼媡悢偺娭學偱偟偨丅偱偡偐傜丄僀儞僺乕僟儞僗偑俀佢侾俀侽亱兌偱偁傟偽丄傾僪儈僞儞僗偼侽丏俆佢乕侾俀侽亱俽偲側傝傑偡丅
侾俀. 暋慺悢偲倕倶倫娭悢
exp乮僄僋僗億乕僱儞僔儍儖乯偲偄偆娭悢偑偁傝傑偡丅僐儞僨儞僒偑曻揹偡傞偲偒偺揹埑傪僌儔僼偵偡傞偲偒丄俤倶們倕倢偱丄=E1*EXP(-T1/C1/R1)偺傛偆偵巊梡偟傑偟偨丅
偙偺exp娭悢偼暋慺悢偱傕巊偊傑偡丅俤倶們倕倢偱乮暘愅僣乕儖傾僪僀儞傪桳岠偵偟偰乯僙儖偵乽=IMEXP("3+4i")乿摍偲擖椡偟傑偡丅乮IMEXP偼暋慺悢偱傕巊偊傞exp娭悢偱偡乯
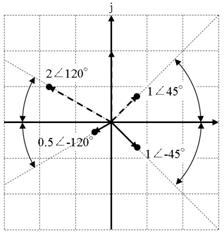
偝偰丄偙偺IMEXP娭悢偵0+2j偺傛偆側乽幚晹偑侽偱丄嫊晹偩偗偑偁傞悢乿傪弴偵擖椡偡傞偲丄壓恾偵帵偡傛偆側丄柺敀偄帠偑婲偒傑偡丅
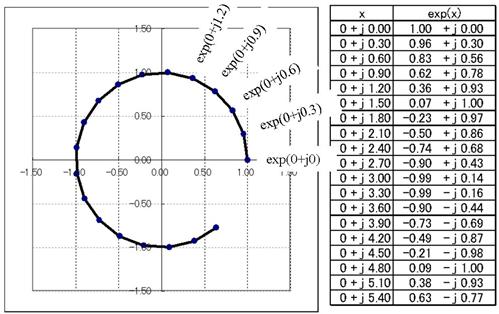
IMEXP偵梌偊傞抣偺丄嫊晹傪彮偟偢偮戝偒偔偟偰峴偔偲丄IMEXP偱媮傔偨寢壥偼丄忋恾偵帵偡偲偍傝丄帪寁偺俁帪偺埵抲偐傜丄敿宎侾偺墌傪昤偄偰夞揮偟偰峴偒傑偡丅偦偟偰丄梌偊傞抣偑倞俇丏俀俉乮偮傑傝丄倞俀兾乯偵側傞偲丄偖傞傝偲堦廃偟偰栠偭偰棃傑偡丅
偙傟偼丄岎棳傪惗傒弌偟偨儁僟儖偺夞揮偲慡偔摨偠傕偺偱偡丅偱偡偐傜丄exp娭悢乮俤倶們倕倢偱偼IMEXP乯偵嫊偺抣傪擖傟偰弌偰偔傞寢壥偼丄傑偝偵岎棳傪昞偟偰偄傑偡丅帪娫t偑宱偰偽宱偮傎偳丄儁僟儖偼夞揮偟偰峴偒傑偡偐傜丄
岎棳 = exp ( j亊帪娫 ) = exp( j t )
乮t偵j傪妡偗偰偄傞偺偼丄嫊晹偩偗偺悢傪嶌傞偨傔偱偡乯
俤倶們倕倢偱偼=IMEXP(COMPLEX(0,帪娫))
忋偺幃偱偼丄俇丏俀俉昩偱堦廃偡傞儁僟儖偟偐昞偣傑偣傫偐傜丄儁僟儖傪夞偡懍偝傪冎偲偡傟偽丄
岎棳 = exp ( j亊夞揮偺懍偝亊帪娫 ) = exp( j冎t )
俤倶們倕倢偱偼=IMEXP(COMPLEX(0,廃攇悢*帪娫))
偲彂偔偙偲偑偱偒傑偡丅乮冎偑戝偒偄掱丄儁僟儖偑憗偔夞揮偟傑偡乯偨偲偊偽丄嵟戝揹埑乮儁僟儖偺挿偝乯俆倁偱丄侾侽俫倸乮侾昩娫偵侾侽夞揮乯偺岎棳揹埑偱偁傟偽丄
嵟戝揹埑俆倁偱侾侽俫倸偺岎棳揹埑 = 5 亊 exp ( j亊俇俀丏俉亊t )乵倁乶
俤倶們倕倢偱偼=5*IMEXP(COMPLEX(0,62.8*帪娫)
乮悢妛偭傐偔彂偗偽乽5 exp (j 62.8 t)乿偁傞偄偼乽5 e j 62.8 t乿偱偡乯
偲偄偆娙扨側寁嶼偱岎棳傪昞偡偙偲偑偱偒傑偡丅sin傗cos摍偺柺搢側嶰妏娭悢偑弌偰偙側偄偺偱丄偲偰傕妝偵巊偊傑偡丅
IMEXP娭悢偺寢壥偐傜丄sin偺攇傪媮傔偨偄偲偒偼丄IMAGINARY(IMEXP(乣))偲嫊晹傪庢傝弌偟丄cos偺攇傪媮傔偨偄偲偒偼丄IMREAL(IMEXP(乣))偲幚晹傪庢傝弌偡偩偗偱偡丅
e偺抣偼栺俀丏俈俀偱丄ejt偼t偑俀兾偺帪偵偒偭偪傝堦廃偟傑偡丅e傛傝彫偝偄2jt偱偼侾堦廃偱偒偢丄3jt偱偼侾廃埲忋夞偭偰偟傑偄傑偡丅偙偺偨傔e偼兾偲暲傫偱乽塅拡偺拋彉傪昞偡悢乿偲峫偊傜偰偄傑偡丅ejt偵斾傋傟偽丄sin(t)傗cos(t)側偳偼乽僓僐娭悢乿偲尵偊傞偱偟傚偆丅
侾. 俤倶們倕倢偱僼僃乕僓偐傜攇宍傪昤偔
椺偊偽壓恾偵帵偡偲偍傝丄係亄倞俁偲偄偆僼僃乕僓偑偁偭偨偲偒丄偦偺攇宍傪庤彂偒偱嶌恾偡傞偙偲偑偱偒傑偡丅
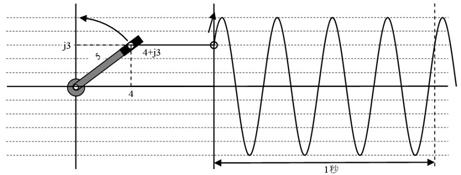
傕偪傠傫偲偰傕庤娫偑妡偐傝傑偡丅偙偺柺搢側嶌恾傕丄俤倶們倕倢傪巊偊偽娙扨偵峴偊傑偡丅
幚偼丄僼僃乕僓偲丄婎杮偺夞揮傪昞偡乽倕倶倫乮倞倲乯乿傪妡偗傞偩偗偱丄僼僃乕僓偑昞偡攇宍傪媮傔傞偙偲偑偱偒傞偺偱偡丅偮傑傝丄
僼僃乕僓丂亊丂倕倶倫乮倞倲乯丂亖丂僼僃乕僓偺昞偡岎棳偺攇偺宍
偱偡丅屻偼丄倲傪偩傫偩傫戝偒偔偟偰寁嶼偟偰傗傟偽丄岎棳偺攇宍偑弌偰偒傑偡丅俤倶們倕倢偱師偺傛偆偵抣傗幃傪擖椡偟偰傒傑偟傚偆丅
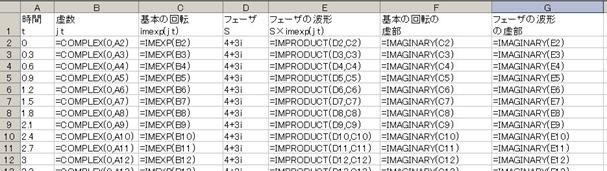
俙楍偑帪娫偱丄彮偟偢偮戝偒偔側偭偰偄傑偡丄俛楍偼帪娫偵倞傪妡偗偰嫊悢偵偟偨傕偺丄俠楍偼倕倶倫乮倞倲乯傪寁嶼偟偰丄婎杮偺夞揮乮敿宎侾偱丄曃妏乮攇偺嵍塃僘儗乯侽乯傪媮傔偨傕偺丄俢楍偼寁嶼偟偨偄岎棳偺僼僃乕僓乮係亄倞俁乯丄俤楍偼僼僃乕僓偲婎杮偺夞揮傪妡偗偨乽僼僃乕僓偺攇宍乿偱偡丅俥楍偲俧楍偼嫊晹傪庢傝弌偟偰丄攇宍傪媮傔偨傕偺偱偡丅
寁嶼寢壥偼壓恾偺傛偆偵側傝傑偡丅
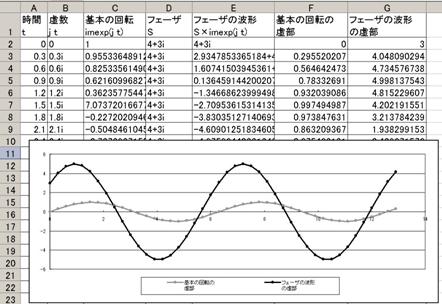
僌儔僼偵偼丄婎杮偺夞揮偺攇宍乮僌儗乕丗俥楍乯偲丄僼僃乕僓偑帵岎棳偺攇宍乮崟丗俧楍乯傪昞帵偟偰偄傑偡丅僌儗乕偺攇宍偼嵟戝抣偑侾偱侽偐傜巒傑傞婎杮偺夞揮傪帵偟偰偄傞偙偲偑暘傝傑偡偟丄崟偺攇宍偼丄嵟戝抣俆偱丄栺俁俈亱埵憡偑恑傫偱偄傑偡丅
偮傑傝乽婎杮偺夞揮偵僼僃乕僓傪妡偗傞偩偗偱丄僼僃乕僓偑昞偡夞揮偑暘傞乿乽夞揮偺嫊晹傪庢傝弌偣偽丄攇宍偑暘傞乿偺偱偡丅
幚晹偱偼側偔丄乽嫊晹傪庢傝弌偣偽丄攇宍偑暘傞乿偪傚偭偲柇偱偡丅偦偺棟桼偼丄帺揮幵傪慜偐傜尒偨忬懺傪婎杮偵峫偊偨偨傔乮儁僟儖偺忋壓偺乮嫊晹偺乯摦偒偑攇宍偵懳墳偟偨偐傜乯偱偡丅傕偟丄帺揮幵傪忋偐傜尒偨忬懺傪婎杮偵峫偊傟偽乮儁僟儖偺慜屻偺乮幚晹偺乯摦偒偑攇宍偵懳墳偡傞偺偱乯乽幚晹傪庢傝弌偣偽丄攇宍偑暘傞乿偙偲偵側傝傑偡丅幚晹丄嫊晹丄偳偪傜傪慖傫偱傕丄尒曽偑堘偆偩偗偱壗傟傕惓偟偄摎偱偡丅乮揹婥偺悽奅偱偼攇宍傪倱倝値娭悢偱昞偡偙偲偑岲傑傟丄們倧倱娭悢偱偼偁傑傝昞偝側偄帠偲傕娭學偑偁傝傑偡乯
俀. 暋慺揹埑丄暋慺揹棳
偙偙傑偱棃傟偽乽暋慺揹埑乿傗乽暋慺揹棳乿傕丄偳偆偣乽婼抺杺墹乿偺拠娫偩側乧偲暘傞偱偟傚偆丅偮傑傝乽柤慜偩偗擄偟偄搝乿偱偡丅
暋慺揹埑傗暋慺揹棳偼丄揹埑傗揹棳傪乽傋僟儖偺嵟弶偺埵抲乮偮傑傝丄僼僃乕僓乯乿偱昞偟偨傕偺丄偱偡丅尵偄曽傪彮偟曄偊傞偲丄僼僃乕僓偱昞偟偨岎棳揹埑偑暋慺揹埑丄僼僃乕僓偱昞偟偨岎棳揹棳偑暋慺揹棳偱偡丅
暅廗偟傑偟傚偆丅岎棳偼壓恾偺傛偆偵丄儁僟儖偺夞揮偱敪惗偟偰偄傑偟偨丅壓恾偺岎棳偼丄僋儔儞僋偺挿偝偑俆丄嵟弶偺埵抲偑栺俁俈亱恑傫偱偄傑偡丅
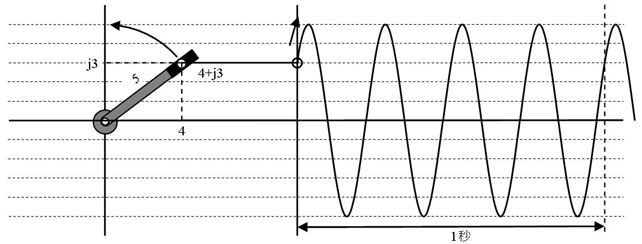
偙偺乽儁僟儖偺嵟弶偺埵抲乿傪丄暋慺悢乮係亄倞俁乯偱昞偟偨傕偺偑乽僼僃乕僓乿偱偟偨丅偦偟偰丄僼僃乕僓偱昞偟偨乽揹埑乿偑乽暋慺揹埑乿丄僼僃乕僓偱昞偟偨乽揹棳乿偑乽暋慺揹棳乿偱偡丅
忋恾偺岎棳偼丄偨偲偊偽揹埑E偱偁傟偽丄僼僃乕僓乮儁僟儖偺嵟弶偺埵抲乯傪巊偭偰丄
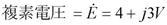
揹棳I偱偁傟偽丄僼僃乕僓乮儁僟儖偺嵟弶偺埵抲乯傪巊偭偰丄
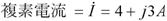
偲昞偡偙偲偑偱偒傑偡丅E傗I偺忋偵晅偄偰偄傞乽丒乿偼丄乽暋慺悢偱偡傛乿乮偮傑傝丄岦偒偑偁傝傑偡傛乯偲偄偆儅乕僋偱丄徣棯偝傟傞偙偲傕偁傝傑偡丅
暋慺揹埑傗揹棳偼乮僼僃乕僓偲摨堦恖暔偱偡偐傜乯戝偒偝偲嵟弶偺妏搙乮埵憡乯偼昞偟偰偄傑偡偑丄廃攇悢偼昞偟偰偄傑偣傫丅
壓恾偺揹埑攇宍偵懳墳偡傞僼僃乕僓傪昤偒丄暋慺揹埑丄嵟戝揹埑丄廃攇悢丄傪婰擖偟偰偔偩偝偄丅乮侾栚惙傝傪侾倁偲偟傑偡乯
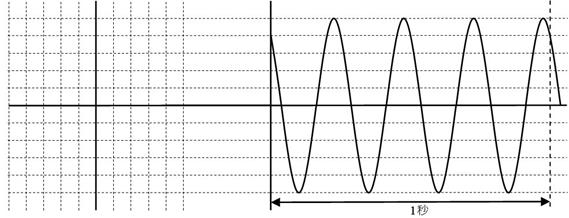
暋慺揹埑丗丂丂丂丂丂倁丂嵟戝揹埑丗丂丂倁丂廃攇悢丗丂丂俫倸
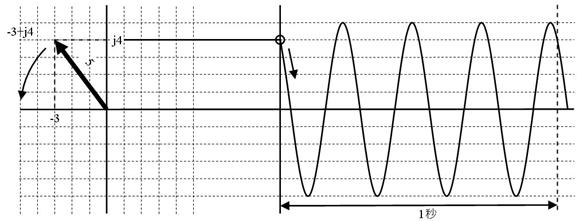
暋慺揹埑丗亅俁亄倞係倁丂嵟戝揹埑丗丂俆倁丂廃攇悢丗丂係俫倸
嵟戝揹埑偼丄攇宍偺嵟戝抣偐傜媮傔傞偙偲傕丄儁僟儖偺挿偝偐傜媮傔傞偙偲傕丄丅暋慺揹埑乮亅俁亄倞俁乯偺愨懳抣乮乥亅俁亄倞係乥亖俆乯傪寁嶼偟偰媮傔傞偙偲傕偱偒傑偡丅
俁. 暋慺揹埑偲揹棳偺僆乕儉懃
壓昞偺傛偆偵丄岎棳偺揹埑傗僀儞僺乕僟儞僗偼丄僔儞僾儖偵俙俠侾侽倁摍偲乽戝偒偝乿偩偗偱昞偡偙偲傕偱偒傑偟偨丅傑偨丄傛傝徻偟偔丄俉亄倞俇倁乮侾侽佢俁俈亱倁乯偲暋慺悢傪巊偭偰乽戝偒偝偲岦偒乿偱昞偡帠傕偱偒傑偟偨丅
|
崁栚
|
戝偒偝偩偗乮抣乯
|
戝偒偝偲岦偒乮暋慺悢)
|
|
柤徧
|
抣偺椺
|
柤徧
|
抣偺椺
|
|
揹埑
|
岎棳揹埑E
|
俙俠侾侽倁
|
暋慺揹埑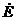
乮揹埑僼僃乕僓乯
|
俉亄倞俇倁
侾侽佢俁俈亱倁
|
|
揹棳
|
岎棳揹棳I
|
俙俠俆俙
|
暋慺揹棳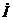
乮揹棳僼僃乕僓乯
|
俁亄倞係俙
俆佢俆俁亱俙
|
|
捠偟擄偝
|
僀儞僺乕僟儞僗Z
|
俀兌
|
暋慺僀儞僺乕僟儞僗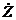
|
1.92亅倞0.56兌
2佢亅16亱兌
|
|
捠偟擄偝
|
傾僪儈僞儞僗Y
|
侽丏俆俽
|
暋慺傾僪儈僞儞僗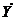
|
0.48亄倞0.14俽
0.5佢16亱俽
|
|
仸暘傝堈偝偺偨傔偵丄俙俠揹埑偲暋慺揹埑偺抣傪懙偊偰傑偡偑丄幚嵺偺嫮偝偼堎側傝傑偡丅俙俠揹埑偼幚岠抣傪帵偟丄僼僃乕僓偺戝偒偝偼嵟戝揹埑傪帵偟傑偡丅
|
偝偰丄岎棳偱傕僆乕儉懃偑巊偊傑偟偨丅偮傑傝丄忋昞偺乽戝偒偝偩偗乿晹暘偵偁傞俙俠侾侽倁丄俙俠俆俙丄俀兌偺娫偱丄
俙俠侾侽倁丂亖丂俙俠俆俙丂亊丂俀兌
偮傑傝丄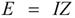
偲丄寁嶼偱偒傑偡丅
偝傜偵忋昞偺乽戝偒偝偲岦偒乿偺晹暘偵偁傞暋慺揹埑乮俉亄倞俇倁乯丄暋慺揹棳乮俁亄倞係俙乯丄暋慺僀儞僺乕僟儞僗乮侾丏俋俀亄倞侽丏俆俇兌乯偺娫偱僆乕儉懃傪巊偭偰丄
俉亄倞俇倁丂亖丂乮俁亄倞係乯俙丂亊丂乮侾丏俋俀亅倞侽丏俆俇乯兌
偮傑傝丄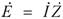
偲丄寁嶼偱偒傑偡丅
俤倶們倕倢偱乽=IMPRODUCT("3+4i","1.92-0.56i")乿偲擖椡偡傞偲丄乽8+6i乿偲丄忋婰偺捠傝偺寢壥偑昞帵偝傟傑偡丅
暋慺悢傪巊偭偨僆乕儉懃偺寁嶼椺傪悢偵帵偟傑偡丅偙偺傛偆偵丄戝偒偝偩偗偱偼側偔丄埵憡乮攇偺僘儗丗曃妏乯傕寁嶼偱偒傑偡丅
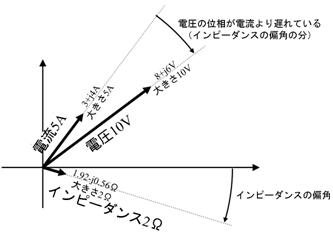
忋恾偱偼丄僀儞僺乕僟儞僗偺曃妏偺暘偩偗丄揹棳傛傝揹埑偺埵憡偑抶傟偰偄傞偙偲偑暘傝傑偡丅偙傟偼丄暋慺悢偱揹棳偲僀儞僺乕僟儞僗傪妡偗偨寢壥丄揹棳偲僀儞僺乕僟儞僗偺曃妏偺崌寁偑揹埑偺曃妏偲側偭偨乮暋慺悢偺妡偗嶼偱偼丄曃妏偑懌偟嶼偵側傞乯偨傔偱偡丅
傕偪傠傫丄暋慺揹棳丄暋慺揹埑丄暋慺僀儞僺乕僟儞僗丄偦傟偧傟偺戝偒偝乮愨懳抣乯偼丄乮曽岦偺側偄乯岎棳揹棳丄僀儞僺乕僟儞僗丄岎棳揹埑偺寁嶼偲堦抳偟傑偡丅
暋慺悢揹埑丒揹棳偱傕巊偊傞偲偼丄僆乕儉懃偼側偐側偐僼僩僐儘偺峀偄朄懃偱偡丅
俁.侾. 楙廗乮暋慺揹埑偺僆乕儉懃乯
壓恾偺夞楬偺俴俼偺暋慺僀儞僺乕僟儞僗偲暋慺揹棳傪媮傔丄壓恾塃懁偺恾偵彂偒崬傫偱偔偩偝偄丅
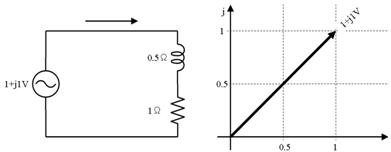
俁.俀. 摎
俤倶們倕倢偱=IMDIV("1+1i","1+0.5")偲寁嶼偟偰丄1.15+0.768i偲暘傞丅偙傟傪壓恾偺傛偆偵婰擖偡傞丅
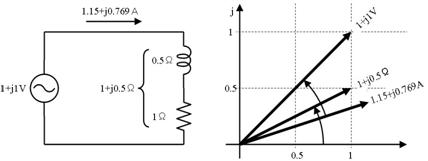
係. 椡棪
壓恾偺夞楬恾偼丄俁兌偺僐僀儖偲係兌偺掞峈偑捈楍偵愙懕偝傟偰偍傝丄僀儞僺乕僟儞僗偺戝偒偝偼俆兌偱偡丅揹尮偑侾侽倁偱偡偐傜丄俀俙偺揹棳偑棳傟傑偡丅
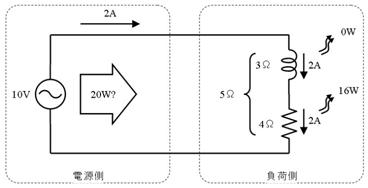
偝偰丄忋恾嵍偺揹尮懁偐傜尒傞偲丄侾侽倁偱俀俙棳傟偰偄傞偺偱丄俀侽倂偺揹椡傪憲傝弌偟偰偄傞傛偆偵巚偊傑偡丅偟偐偟丄忋恾塃偺晧壸懁偱尒傞偲丄乮僐僀儖偼揹棳偑棳傟偰傕敪擬偟傑偣傫偐傜乯係兌偵俀俙棳傟偰丄侾俇倂偺揹椡傪徚旓偡傞偩偗偱偡丅
忋恾嵍懁偺傛偆偵丄揹棳偲揹埑傪妡偗偰寁嶼偟偨乮尒偐偗偺乯揹椡傪乽旂憡揹椡乿偲屇傃丄忋恾塃懁偺傛偆偵丄杮摉偵徚旓偝傟偨揹椡傪乽桳岠揹椡乿偲屇傫偱丄憃曽傪嬫暿偟傑偡丅乮乽旂憡揹椡乿偲偼擄偟偄尵偄曽偱偡偑丄塸岅偺apparent power偮傑傝乽尒偨栚偺揹椡乿傪柪栿偟偨傕偺偱偡丅乯
旂憡揹椡傗桳岠揹椡偺堄枴傗扨埵偼師昞偺偲偍傝偱偡丅
|
柤慜
|
堄枴
|
扨埵
|
扨埵偺屇傃曽
|
|
旂憡揹椡
|
揹棳偲揹埑偺戝偒偝傪妡偗偨
尒偨栚偺揹椡
|
倁俙
|
儃儖僩傾儞儁傾
偁傞偄偼丂僽僀僄乕
|
|
桳岠揹椡
|
杮摉偵徚旓偝傟偨揹椡
|
倂
|
儚僢僩
|
傕偪傠傫丄旂憡揹椡偲桳岠揹椡偺嵎偑戝偒偄偲丄揹棳傗揹埑偼戝偒偄偺偵丄徚旓揹椡偑彮側偔側傝丄晄宱嵪偱偡丅偱偡偐傜丄偱偒傞偩偗旂憡揹椡偲桳岠揹椡偑摨偠偵側傞傛偆偵岺晇偟傑偡丅
偦偺岺晇偺栚埨偲偟偰丄桳岠揹椡亐旂憡揹椡偺抣傪乽椡棪乿偲屇傫偱巊梡偟傑偡丅椡棪偑侾乮侾侽侽亾乯側傜丄桳岠揹椡亖旂憡揹椡偱丄尒偨栚偺揹椡偼丄偡傋偰桳岠偵徚旓偝傟偰偄傑偡丅椡棪偑俆侽亾側傜丄尒偨栚偺揹椡偺敿暘偟偐桳岠妶梡偝傟偰偄傑偣傫丅
椡棪偺寁嶼偵偼怓乆側曽朄偑偁傝傑偡丅壓恾偺夞楬傪椺偵丄壓昞偱愢柧偟傑偡丅
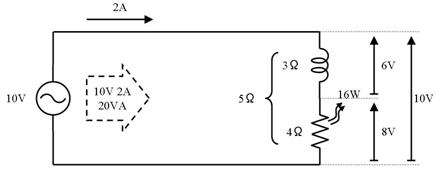
忋昞偺嘆乣嘋偺拞偐傜乽崱丄暘偭偰偄傞抣乿乽偦偺偲偒媮傔傗偡偄抣乿偑巊偊傞曽朄傪慖傫偱寁嶼偟傑偡丅
偲偙傠偱丄嘋偺曽朄偼丄偙偺椺偱偼柺搢側偩偗偱榑奜偱偡丅偦傟偵傕娭傢傜偢宖嵹偟偨偺偼乽椡棪乿偺帠傪乽們倧倱兤乿偲屇傇恖偑懡偄偐傜偱偡丅偙傟偼丄乽椡棪偑丄僀儞僺乕僟儞僗偺曃妏兤偺們倧倱偺抣偱偁傞乿帠偐傜棃偨屇傃柤偱偡偑丄偙偺屇傃曽偱偼乽兤偑壗偺妏搙側偺偐乿暘傜側偄偨傔丄乽椡棪乿傛傝傕晄惤幚側屇傃曽偵巚偊傑偡丅乮僶僀僋偺塣揮庤傪丄扨偵乽塣揮庤乿偲屇傫偱偄傞傛偆側傕偺偱偡丅乽塣揮庤傪楢傟偰偒偰偔傟乿偲棅傫偩偺偱偼丄帺摦幵偺塣揮庤偑棃傞偐傕抦傟傑偣傫乯偦傟偵傕偐偐傢傜偢丄彂愋偱傕巊傢傟傞懠丄岥摢偱傕乽僐僒僀儞僔乕僞傪應掕偟偲偄偰偔傟乿摍偲巊傢傟偰偄傑偡丅
係.侾. 楙廗
壓恾偺夞楬偺椡棪傪媮傔偰壓偝偄丅
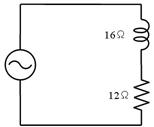
椡棪丂丂丂丂丂亾
係.俀. 摎
僀儞僺乕僟儞僗偑暘偭偰偄傞偺偱丄忋昞嘊偺曽朄偱寁嶼偟傑偡丅
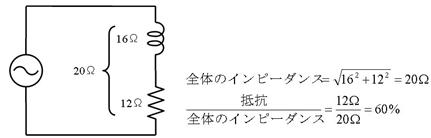
椡棪丂俇侽亾丂亾
俆. 暋慺揹椡
暋慺揹埑偵僆乕儉懃偑巊偊偨傛偆偵丄暋慺揹埑偲暋慺揹棳偐傜暋慺揹椡傪媮傔傞偙偲傕偱偒傑偡丅偨偲偊偽丄壓恾偺傛偆偵俉亄倞俇倁偱係亅倞俁俙偑棳傟偨応崌偼丄
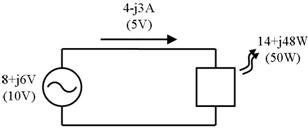
俤倶們倕倢偱丄=IMPRODUCT("8+6i","4+3i")偲擖椡偡傞帠偱丄暋慺揹椡偑14+58i偲寁嶼偝傟傑偡丅揹棳偺乽俁亅倞係乿偺倞偺晹暘乮嫊晹乯偺晞崋傪斀揮偟偰乽俁亄倞係乿偲擖椡偡傞揰偵拲堄偟傑偡丅乮棟桼偼屻弎偟傑偡乯
偙偆偟偰媮傔偨暋慺揹椡傪壓恾偵帵偟傑偡丅恾偱暘傞傛偆偵丄暋慺揹椡偼丄桳岠揹椡乮幚晹乯傕旂憡揹椡乮愨懳抣乯傕昞尰偟偰偄傑偡丅偝傜偵丄暋慺揹椡偺嫊晹偼乽柍岠揹椡乿偲屇偽傟偰偄傑偡丅偙偺傛偆偵丄暋慺揹椡偼岎棳揹椡偺怓乆側梫慺傪堦敪偱昞偡偙偲偑偱偒傑偡丅
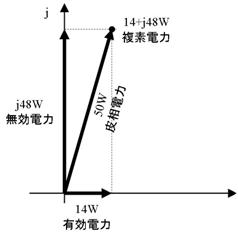
偝偰丄暋慺揹椡傪媮傔傞偲偒偵丄揹棳偺嫊晹傪媡晞崋偵偟傑偟偨丅偪傚偭偲晄帺慠偱偡丅偦偺棟桼偼丄壓恾偺傛偆側丄揹棳偲揹埑偺埵憡偑摨偠応崌傪峫偊傞偲棟夝偱偒傑偡丅揹棳偲揹埑偺埵憡偑摨偠側傜丄桳岠揹椡偩偗偑敪惗偟偰丄柍岠揹椡偼敪惗偟側偄乮椡棪偑侾侽侽亾偵側傞乯敜偱偡丅
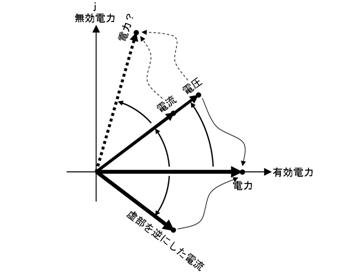
偝偰丄揹埑偲揹棳偺妡偗嶼偱偼丄揹棳偲揹埑偺曃妏偑崌寁偝傟傞偨傔丄偦偺傑傑妡偗傞偲忋恾偵揰慄偱帵偡揹椡偺傛偆偵丄柍岠側惉暘乮忋岦偒偺惉暘乯偑戝敿偲側傝傑偡丅
偲偙傠偑丄揹棳偺嫊晹傪媡晞崋偵偟偰寁嶼偟偰傗傞偲丄揹埑偺曃妏偼忋岦偒乮亄乯丄揹棳偺曃妏偼壓岦偒乮亅乯偱丄妡偗傞偲乮妡偗嶼偼丄曃妏偺懌偟嶼側偺偱乯懪偪徚偟偁偭偰曃妏偑僛儘偲側傝丄忋恾偵幚慄偱帵偡揹椡偺傛偆偵丄偪傚偆偳塃岦偒偺桳岠揹椡偩偗偵側傝傑偡丅
偮傑傝丄暋慺揹椡傪媮傔傞偲偒偵揹棳偺嫊晹傪媡晞崋偵偡傞棟桼偼丄揹埑偲揹棳偺埵憡偑摨偠偲偒偵丄桳岠揹椡偩偗偑摼傜傟傞傛偆偵偡傞偨傔偱偡丅
俆.侾. 楙廗
俤倶們倕倢傪梡偄偰丄壓恾偺夞楬偺晧壸偱敪惗偡傞暋慺揹椡傪媮傔丄桳岠揹椡丄柍岠揹椡丄旂憡揹椡傪寁嶼偟偰偔偩偝偄丅
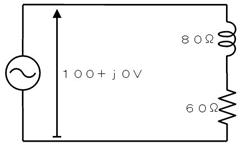
暋慺揹椡丂丂丂丂丂丂倂丂桳岠揹椡丂丂丂丂倂丂柍岠揹椡丂丂丂丂倁俙丂旂憡揹椡丂丂丂丂倁俙
俆.俀. 摎
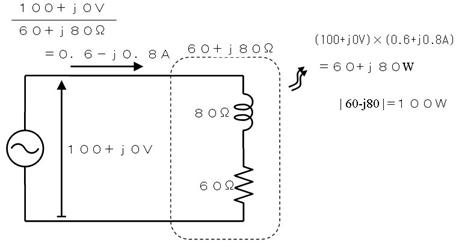
暋慺揹椡俇侽亄倞俉侽倂丂桳岠揹椡丂丂俇侽倂丂柍岠揹椡丂丂俉侽倁俙丂旂憡揹椡丂侾侽侽倁俙
暋慺揹棳偼俤倶們倕倢偱=IMDIV("100+0i","60+80i")偱侽丏俇亅倞侽丏俉俙
暋慺揹椡偼俤倶們倕倢偱=IMPRODUCT("100+0i","0.6+0.8i")
偁傞偄偼丄=IMPRODUCT("100+0i",IMCONJUGATE(IMDIV("100+0i","60+80i")))偱俇侽亄倞俉侽倂
彯丄暋慺揹椡偼揹棳傪寁嶼偣偢偵丄

偱傕寁嶼偱偒傑偡丅
丂俤仏偼俤偺嫊晹偺晞崋傪媡偵偟偨乮嫟栶偺乯悢偱偡丅俤倶們倕倢偱偼IMCONJUGATE()偱偡丅
俤倶們倕倢偱偼丄=IMDIV(IMPRODUCT("100+0i",IMCONJUGATE("100+0i")),"80+80i")偱寁嶼偱偒傑偡丅傕偪傠傫丄偙偺椺偱偼揹埑偺嫊晹偑僛儘側偺偱丄IMCONJUGATE偑側偔偰傕摨偠寢壥偑弌傑偡丅
丂
侾. 廃攇悢偼屻偱寛傔傞
廃攇悢偑堦掕偺揹椡暘栰摍偱偁傟偽丄椺偊偽乽偙偺僐僀儖偼倞俀兌乿偲丄梊傔媮傔偨僀儞僺乕僟儞僗偱寁嶼偡傞偙偲偑偱偒傑偡丅
椺偊偽壓恾嵍懁偱偼丄廃攇悢偑侽丏侾俆俋俫倸偲堦掕偱偁傝丄俀俫偺僐僀儖偼倞俀兌偲寛傑偭偰偄傑偡丅偱偡偐傜丄揹埑偑侾侽亄倞侽倁偱偁傟偽丄夞楬偵棳傟傞揹棳偼丄恾拞偺寁嶼偵傛傝丄亅倞俆俙偲暘傝傑偡丅
偦偺寢壥丄摨恾嵍壓偺僼僃乕僓偱帵偡傛偆偵丄揹埑傛傝俋侽亱抶傟偰丄戝偒偝偑俆俙偺揹棳偑棳傟傞偲媮傔傞偙偲偑偱偒傑偡丅
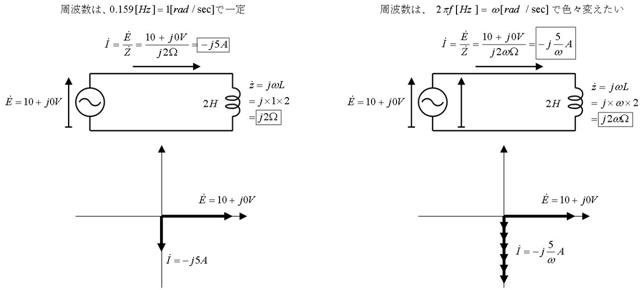
偲偙傠偑僆乕僨傿僆夞楬摍偺乽條乆側廃攇悢偺岎棳傪埖偄偨偄乿夞楬偱偼丄偙偺傛偆偵廃攇悢傪寛傔懪偪偡傞偙偲偑偱偒傑偣傫丅廃攇悢偼曄悢偵偟偰偍偄偰丄屻偱怓乆側廃攇悢偱寁嶼偟偨偄偐傜偱偡丅偦偙偱丄廃攇悢傪寛傔懪偪偣偢丄妏廃攇悢冎偺傑傑巆偟傑偡丅
妏廃攇悢冎偺戙傢傝偵丄廃攇悢f傪巊偭偰傕椙偄偺偱偡偑丄妏廃攇悢側傜冎俴偱嵪傓偲偙傠傪丄廃攇悢偱偼2兾倖俴偲彂偐側偔偰偼側傜側偄偨傔丄庤娫傪徣偔偨傔偵妏廃攇悢偑巊傢傟傑偡丅
冎傪巊偆偲丄忋恾塃懁偺傛偆偵丄僐僀儖偺僀儞僺乕僟儞僗偼倞俀冎兌丄偲側傝丄偦偺寢壥夞楬偵棳傟傞揹棳偼丄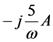 偲側傝傑偡丅
偲側傝傑偡丅
偙偺傛偆偵偟偰丄堦扷丂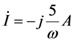 傪媮傔偰偍偗偽丄椺偊偽妏廃攇悢冎偑侾侽侽侽rad/sec偺応崌乮偮傑傝侾俆俋俫倸偺応崌乯偼丄
傪媮傔偰偍偗偽丄椺偊偽妏廃攇悢冎偑侾侽侽侽rad/sec偺応崌乮偮傑傝侾俆俋俫倸偺応崌乯偼丄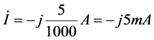 偲丄廃攇悢偵墳偠偰棳傟傞揹棳傪娙扨偵媮傔傞偙偲偑偱偒傑偡丅
偲丄廃攇悢偵墳偠偰棳傟傞揹棳傪娙扨偵媮傔傞偙偲偑偱偒傑偡丅
偙偺傛偆偵丄廃攇悢傪屻偱寛傔傞傛偆偵偡傞偲丄幃偑擖傝慻傫偱棃傑偡丅妛峑偱悢幃偵鐒堈偟偨曽偼丄乽悢妛偑嬯庤偩偲嬯偟偦偆偩側乿偲巚偆偐傕偟傟傑偣傫偑丄慡偔偦傫側偙偲偼偁傝傑偣傫丅
傑偢丄僆乕儉懃偱揹棳傗揹棳傪媮傔偨傝丄僀儞僺乕僟儞僗偺懌偟嶼傪偟偨傝偡傞寁嶼偑慻傒崌傢偝傟偰偄傞偩偗偡偐傜丄乽巐懃墘嶼乿偟偐弌偰偒傑偣傫丅
偝傜偵丄乽幃偑弌偰偒偨傜丄鉟楉偵曄宍偟偰惍棟偟側偗傟偽側傜側偄乿乮妛峑偱偦偆尵傢傟偨偐傜乯偲巚偄彑偪偱偡偑丄偦偺昁梫偑柍偄偺偱偡丅嵟弶偵嶌偭偨宍偺傑傑俤倶們倕倢偵擖椡偟偰丄寢壥傪寁嶼偝偣傟偽椙偄偐傜偱偡丅
俁. 夞楬偺弌椡揹埑傪媮傔傞
壓恾嵍懁偺夞楬偺擖椡偵丄僼僃乕僓乮戝偒偝偲埵憡乯偑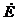 偱丄妏廃攇悢冎偺岎棳傪壛偊偨偲偒偺弌椡傪媮傔傑偡丅
偱丄妏廃攇悢冎偺岎棳傪壛偊偨偲偒偺弌椡傪媮傔傑偡丅
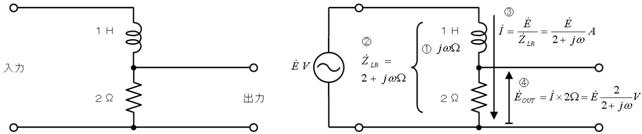
忋恾塃懁偺嘆嘇嘊乧偺弴偱峫偊傑偡丅
嘆侾俫偺僐僀儖偺僀儞僺乕僟儞僗偼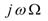 偱偡丅乮
偱偡丅乮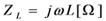 乯
乯
嘇僐僀儖偲掞峈偺捈楍崌惉僀儞僺乕僟儞僗偼丄憃曽偺僀儞僺乕僟儞僗傪崌寁偟偰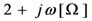 偱偡丅
偱偡丅
嘊擖椡偵岎棳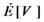 傪壛偊偨偲偒偵丄捈楍夞楬偵棳傟傞揹棳偼丄
傪壛偊偨偲偒偵丄捈楍夞楬偵棳傟傞揹棳偼丄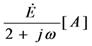 偱偡丅
偱偡丅
忋偱媮傔偨揹棳偑丄俀兌偺掞峈偵棳傟偰敪惗偡傞揹埑偑丄乽弌椡揹埑乿偱偡偐傜丄
嘋弌椡揹埑偼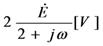 丄偪傚偭偲曄宍偟偰乮昁恵偱偼偁傝傑偣傫乯
丄偪傚偭偲曄宍偟偰乮昁恵偱偼偁傝傑偣傫乯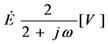 偲側傝傑偡丅
偲側傝傑偡丅
偨偲偊偽丄妏廃攇悢冎偑侾rad/sec乮侽丏侾俇俫倸乯偱丄擖椡偑侾侽亄倞侽 [V]偺応崌偺弌椡揹埑偼丄俤倶們倕倢偺僙儖偵丄=IMPRODUCT(2,IMDIV(10,"2+i"))丄偲擖椡偡傟偽丄俉亅倞係偲昞帵偝傟傑偡丅乮暋慺悢偺寁嶼偼俤倶們倕倢偑傗傝傑偡偐傜丄庤寁嶼偼偁傑傝昁梫偱偼偁傝傑偣傫丅乯
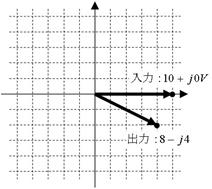
俁.侾. 楙廗
壓恾偺夞楬偺擖椡偵丄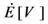 乮妏廃攇悢冎乯傪壛偊偨偲偒偵丄弌椡偵尰傟傞揹埑傪丄壓昞偺嬻棑傪婰擖偟偰峫偊偰偔偩偝偄丅傑偨丄侾侽亄倞侽倁傪擖椡偵壛偊偨応崌偺弌椡揹埑偺僼僃乕僓傪壓恾塃懁偵彂偒崬傫偱壓偝偄丅乮偙偺夞楬偼乽俠俼旝暘夞楬乿偲屇偽傟偰偄傑偡乯
乮妏廃攇悢冎乯傪壛偊偨偲偒偵丄弌椡偵尰傟傞揹埑傪丄壓昞偺嬻棑傪婰擖偟偰峫偊偰偔偩偝偄丅傑偨丄侾侽亄倞侽倁傪擖椡偵壛偊偨応崌偺弌椡揹埑偺僼僃乕僓傪壓恾塃懁偵彂偒崬傫偱壓偝偄丅乮偙偺夞楬偼乽俠俼旝暘夞楬乿偲屇偽傟偰偄傑偡乯
丂丂丂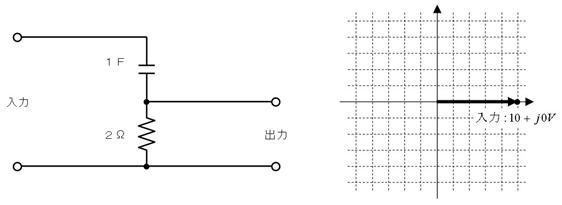
|
侾俥偺僐儞僨儞僒偺丄妏廃攇悢冎偱偺暋慺僀儞僺乕僟儞僗偼丄
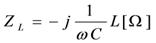 傛傝丄 傛傝丄
|
|
|
僐儞僨儞僒偲掞峈偺捈楍崌惉僀儞僺乕僟儞僗偼丄憃曽偺僀儞僺乕僟儞僗傪崌寁偟偰丄
|
|
|
擖椡偵岎棳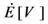 傪壛偊偨偲偒偵丄捈楍夞楬偵棳傟傞揹棳偼丄 傪壛偊偨偲偒偵丄捈楍夞楬偵棳傟傞揹棳偼丄
|
|
|
忋偱媮傔偨揹棳偑丄俀兌偵棳傟偰敪惗偟偨揹埑偑弌椡揹埑偱偡偐傜丄弌椡揹埑偼丄
|
|
|
偨偲偊偽丄侾侽亄倞侽倁丄妏廃攇悢侾rad/sec乮侽丏侾俇俫倸乯偺揹埑傪擖椡偟偨応崌偺弌椡偼丄俤倶們倕倢傪梡偄偰丄
|
|
俁.俀. 摎
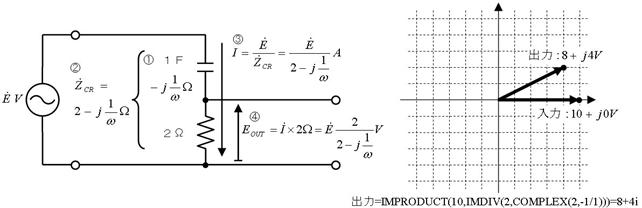
|
侾俥偺僐儞僨儞僒偺丄妏廃攇悢冎偱偺暋慺僀儞僺乕僟儞僗偼丄
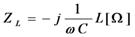 傛傝丄 傛傝丄
|
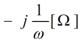
|
|
僐儞僨儞僒偲掞峈偺捈楍崌惉僀儞僺乕僟儞僗偼丄憃曽偺僀儞僺乕僟儞僗傪崌寁偟偰丄
|
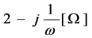
|
|
擖椡偵岎棳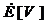 傪壛偊偨偲偒偵丄捈楍夞楬偵棳傟傞揹棳偼丄 傪壛偊偨偲偒偵丄捈楍夞楬偵棳傟傞揹棳偼丄
|
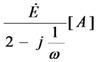
|
|
忋偱媮傔偨揹棳偑丄俀兌偵棳傟偰敪惗偟偨揹埑偑弌椡揹埑偱偡偐傜丄弌椡揹埑偼丄
|
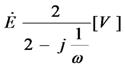
|
|
偨偲偊偽丄侾侽亄倞侽倁丄妏廃攇悢侾rad/sec乮侽丏侾俇俫倸乯偺揹埑傪擖椡偟偨応崌偺弌椡偼丄俤倶們倕倢偺僙儖偵丄
=IMPRODUCT(2,IMDIV(10,"2+i"))
偲擖椡偟偰丄
|
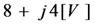
|
係. 廃攇悢偵傛傞弌椡偺曄壔
偝偰丄廃攇悢傪寛傔懪偪偣偢偵丄妏廃攇悢冎偱昞偟偨偺偼乽偁偲偱廃攇悢傪曄偊偰怓乆寁嶼偡傞乿偨傔偱偟偨丅偦傟偱偼幚嵺偵丄楙廗栤戣偱埖偭偨壓恾偺夞楬偵丄條乆側廃攇悢乮妏廃攇悢乯偺岎棳乮僼僃乕僓偼侾侽亄倞侽倁乮戝偒偝侾侽倁偱丄儁僟儖偼嵟弶塃岦偒乯偲偟傑偡乯傪壛偊偰丄弌椡偑偳偺傛偆偵曄壔偡傞偐妋擣偟傑偡丅
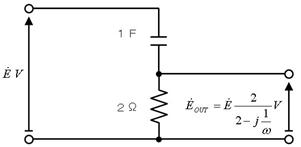
楙廗栤戣偺摎偐傜丄弌椡偼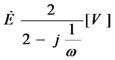 偲暘偭偰偄傑偡丅偙偺幃偼丄俤倶們倕倢偱丄
偲暘偭偰偄傑偡丅偙偺幃偼丄俤倶們倕倢偱丄
=IMPRODUCT(乽擖椡乿,IMDIV(2,IMSUB(2,IMDIV("i",乽冎乿))))
偺傛偆偵寁嶼偱偒傑偡丅偁偲偼丄乽擖椡乿乮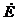 乯傪梌偊偰丄乽冎乿傪彮偟偢偮曄偊偰寢壥傪娤嶡偡傞偩偗偱偡丅偙偙偱偼擖椡偼侾侽亄倞侽乮偮傑傝=COMPLEX(10,0)乯偱丄冎偼俙楍偱巜掕偟傑偡丅
乯傪梌偊偰丄乽冎乿傪彮偟偢偮曄偊偰寢壥傪娤嶡偡傞偩偗偱偡丅偙偙偱偼擖椡偼侾侽亄倞侽乮偮傑傝=COMPLEX(10,0)乯偱丄冎偼俙楍偱巜掕偟傑偡丅
傑偡丄俤倶們倕倢偵壓恾偺傛偆偵擖椡偟傑偡丅俙楍埲奜偺僙儖偼丄堦峴擖椡偟偰壓岦偒偵僐僺乕偡傞偩偗偱偡丅俙楍乮妏廃攇悢乯偺僙儖偼嵟弶偺俇峴傪擖椡偟懠偺抣丄俈峴栚傪擖椡偟偰乮俈峴栚偩偗傪乯壓岦偒偵僐僺乕偟傑偡丅
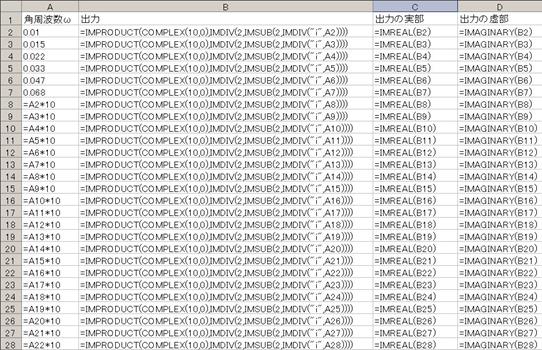
偡傞偲丄寁嶼寢壥偼壓恾偺傛偆偵側傝傑偡丅弌椡偺幚晹偲弌椡偺嫊晹傪乽嶶晍恾乿偱僌儔僼偵昤偄偰偄傑偡丅僌儔僼偺忋偵丄夁嫀偺楙廗栤戣偱寁嶼偟偨妏廃攇悢乮冎亖侾乯偺弌椡偺僼僃乕僓乮俉亄倞係乯傪彂偒壛偊偰偄傑偡丅
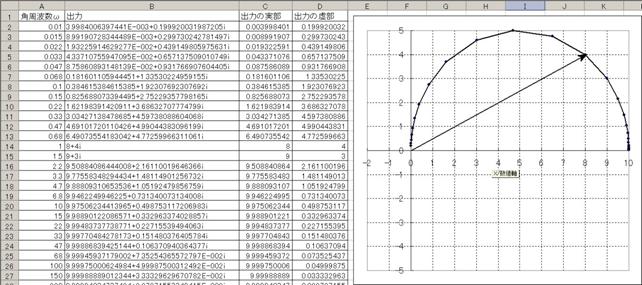
忋恾偺僌儔僼傪尒傟偽丄廃攇悢偑曄傢傞偲弌椡偺僼僃乕僓偑偳偺傛偆偵曄壔偡傞偐暘傝傑偡丅偮傑傝丄廃攇悢偑掅偄乮冎偑彫偝偄乯偲偒偼丄弌椡傕偲偰傕彫偝偄偱偡偑丄廃攇悢偑崅偔側傞偵偮傟偰丄敿墌傪昤偄偰帪寁夞傝偵弌椡偑戝偒偔側偭偰峴偒丄冎亖侾乮楙廗栤戣偱埖偭偨応崌乯偵丄俉亄倞係倁偑弌椡偝傟傑偡丅乮戝偒偝偼栺俋倁乯丅偦偟偰丄廃攇悢偑廫暘崅偔側傞偲丄傎傏侾侽倁偑弌椡偝傟傞偲暘傝傑偡丅
俆. 弌椡偺戝偒偝乮愨懳抣乯偲埵憡乮曃妏乯
忋偱嶌惉偟偨俤倶們倕倢僔乕僩偺堦晹乮乽弌椡偺幚晹乿偲乽弌椡偺嫊晹乿偺晹暘乯傪曄峏偟偰丄壓恾偺傛偆偵乽弌椡偺愨懳抣乿乮戝偒偝乯偲乽弌椡偺曃妏乿乮埵憡乯傪昞帵偝偣傑偡丅

寁嶼寢壥偼壓恾偺傛偆偵側傝傑偡丅廃攇悢傪墶幉乮懳悢乯偵丄愨懳抣乮懳悢乯偲曃妏傪廲幉偵丄嶶晍恾僌儔僼傪嶌惉偟偰偄傑偡丅乮僌儔僼偱偼乽懳悢乿偲乽戞俀幉乿偺婡擻傪巊偭偰偄傑偡乯
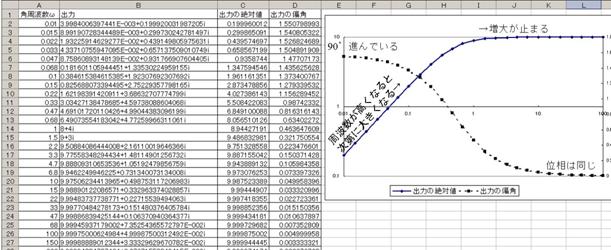
僌儔僼傪尒傞偲丄愨懳抣乮弌椡揹埑偺戝偒偝乯偼丄廃攇悢偑崅偔側傞偲師戞偵戝偒偔側傝傑偡偑丄冎偑侾偺偁偨傝偱憹戝偑巭傑傝丄偦傟埲忋廃攇悢偑崅偔側偭偰傕丄杦偳曄壔偟側偄偙偲偑暘傝傑偡丅
傑偨埵憡偼丄廃攇悢偑掅偄応崌偼侾丏俇rad掱搙乮俋侽亱乯恑傫偱偄傑偡偑丄廃攇悢偑崅偔側傞偲丄傎傏 侽亱乮擖椡偟偨揹埑偲摨偠曽岦偺僼僃乕僓偑弌椡偝傟傞乯偲暘傝傑偡丅
俆.侾. 楙廗
壓恾偺夞楬偵侾侽亄倞侽倁偺擖椡揹埑傪壛偊丄冎傪曄壔偝偣偨偲偒偺丄弌椡僼僃乕僓偺曄壔丄弌椡偺戝偒偝乮愨懳抣乯偺曄壔丄弌椡埵憡偺曄壔傪丄俤倶們倕倢傪巊偭偰僌儔僼偵昞帵偟偰偔偩偝偄丅
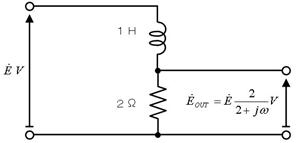
俆.俀. 摎
壓恾傛偆偵俤倶們倕倢偵擖椡偟傑偡丅

寁嶼寢壥偼壓恾偺傛偆偵側傝傑偡丅
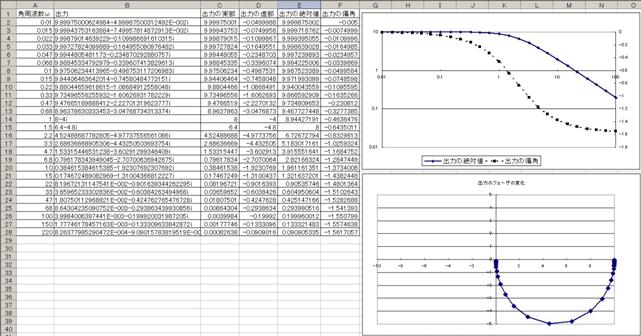
廃攇悢偑崅偔側傞偲丄弌椡偑彫偝偔側傝丄埵憡偑抶傟偰峴偔偙偲偑暘傝傑偡丅
俇. 廃攇悢揱払娭悢
乽廃攇悢揱払娭悢乿偼岆夝偟堈偄柤慜偱偡丅乽廃攇悢傪揱払偡傞條巕傪昞偡娭悢乿偱偼偁傝傑偣傫丅乽廃攇悢偱憹暆棪乮偮傑傝丄擖椡偺弌椡傊偺揱払乯偑曄壔偡傞條巕傪昞偡娭悢乿偲偄偆堄枴偱偡丅椺偊偽乽侾侽侽俫倸偱憹暆棪偼壗攞偱偡偐乿偲暦偗偽乽俁攞偱偡乿摍偲摎偊偰偔傟傞幃偺偙偲偱偡丅
偝偰丄壓恾偵俁攞偺憹暆婍傪帵偟傑偡丅侾丏俆倁傪擖椡偡傞偲丄俁攞偝傟偰丄係丏俆倁偑弌椡偝傟偰偄傑偡丅偙偺傛偆偵憹暆婍偱偼丄椺偊偽乽俁攞乿摍偲丄乽憹暆棪乿偑廳梫側惈擻偱偡丅媡偵丄憹暆棪偑俁攞偲暘偭偰偄傟偽丄侾侽倁擖椡偡傟偽丄俁侽倁偑弌椡偝傟傞乮偮傑傝丄擖椡亊攞棪亖弌椡乯偲寁嶼偡傞偙偲傕偱偒傑偡丅
偲偙傠偱偙偺乽憹暆棪乿偼丄弌椡傪擖椡偱妱偭偰媮傔偨傕偺偱偡丅偮傑傝丄弌椡傪擖椡偱妱傟偽丄偦偺夞楬偺廳梫側惈幙傪昞偡偙偲偑偱偒傞偺偱偡丅
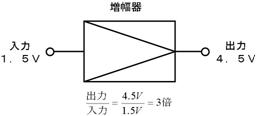
擖椡傗弌椡偼丄揹埑偱傕揹棳偱傕峔偄傑偣傫丅椺偊偽丄揹棳傪擖椡偡傟偽丄揹埑傪弌椡偡傞夞楬傕偁傝傑偡丅偟偐偟偙偙偱偼乽揹埑傪擖椡偟偰丄揹埑傪弌椡偡傞乿乮椙偔偁傞乯夞楬偩偗傪峫偊傑偡丅
偲偙傠偱丄怣崋乮擖椡傗弌椡乯偵偼丄捈棳傗岎棳摍偺條乆側庬椶偑偁傝傑偡丅偦偙偱師昞偵丄奺庬偺怣崋偺庬椶枅偵丄弌椡傪擖椡偱妱偭偨抣偺椺傪帵偟傑偡丅
弌椡亐擖椡偺怓乆
|
怣崋庬椶
|
捈棳揹埑
|
岎棳
|
|
岎棳揹埑
乮戝偒偝乯
|
暋慺揹埑
乮廃攇悢屌掕乯
|
暋慺揹埑
乮屻寛傔廃攇悢冎乯
|
|
擖椡偺椺
|
1.5VDC
|
1.5VAC
|
10+j0V
|
10+j0V
|
|
弌椡偺椺
|
4.5VDC
|
4.5VAC
|
8-j4V
|
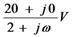
|
|
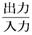
|
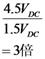
|
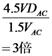
|
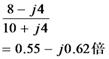
|
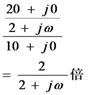
|
|
柤慜
|
捈棳揹埑憹暆棪
|
岎棳揹埑憹暆棪
|
(暋慺揹埑憹暆棪丠)
|
廃攇悢揱払娭悢
|
忋昞堦斣塃懁偺乽廃攇悢乮冎乯傪屻偐傜寛傔偰寁嶼偱偒傞丄暋慺揹埑偺憹暆棪乮弌椡亐擖椡乯傪乽廃攇悢揱払娭悢乿偲屇傃傑偡丅
彯丄忋昞塃懁偼楙廗栤戣偱庢傝忋偘偨丄壓恾偺夞楬傪昞偟偰偄傑偡丅
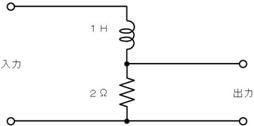
偝偰丄乽憹暆棪乿傕乽揱払娭悢乿傕丄弌椡亐擖椡偱媮傔傞揰偱偼丄摨偠拠娫偱偟偨丅壓恾嵍懁偵乽憹暆棪乿丄摨恾塃懁偵乽揱払娭悢乿偺椺傪帵偟傑偡丅
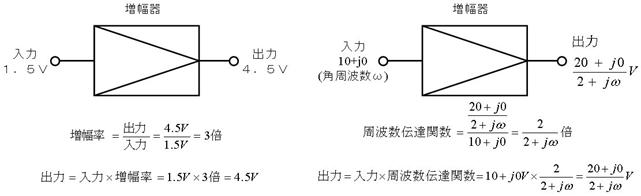
忋恾嵍懁偺椺偱偼丄弌椡偺係丏俆倁傪擖椡偺侾丏俆倁偱妱偭偰丄憹暆棪偺俁攞傪媮傔偰偄傑偡丅媡偵丄擖椡偺侾丏俆倁偵憹暆棪偺俁攞傪妡偗傞偲丄弌椡偺係丏俆倁傪寁嶼偱偒傑偡丅
忋恾塃懁偺椺偱偼丄弌椡偺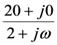 倁傪擖椡偺
倁傪擖椡偺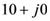 倁偱妱偭偰丄揱払娭悢偺
倁偱妱偭偰丄揱払娭悢偺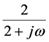 傪媮傔偰偄傑偡丅媡偵丄擖椡偺
傪媮傔偰偄傑偡丅媡偵丄擖椡偺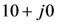 倁偵揱払娭悢偺
倁偵揱払娭悢偺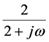 傪妡偗傞偲丄弌椡偺
傪妡偗傞偲丄弌椡偺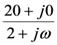 倁傪寁嶼偱偒傑偡丅
倁傪寁嶼偱偒傑偡丅
偙偙偵搊応偡傞傛偆側暋慺悢偺暘悢傪偝傜偵曄宍偟偰丄尒堈偔惍棟偟偨偄偲偄偆梸朷偵嬱傜傟傞曽傕懡偄偱偟傚偆丅傕偪傠傫偦傟偵傛偭偰俤倶們倕倢偺擖椡偼懡彮妝偵側傝傑偡偑丄曄宍偺搑拞偵娫堘偊傞帠傪峫偊傟偽丄幃偼偁傑傝曄宍偣偢偵丄偄偒側傝俤倶們倕倢偵擖傟傞偺傕傾儕偱偡丅偙偙偱偼幃偺曄宍偑寵偄側曽偺偨傔偵丄偁偊偰杦偳曄宍偣偢偵曻抲偟傑偡丅
偮傑傝廃攇悢揱払娭悢偼丄乽憹暆棪乿偵丄乮侾乯廃攇悢傪屻偱寛傔傜傟傞傛偆偵冎偱杽傔崬傫偱丄乮俀乯乽戝偒偝乮俁攞偲偐乯乿偩偗偱偼側偔乽埵憡乮曽岦乯乿傕杽傔崬傫偩丄傕偺偱偡丅尵偭偰傒傟偽乽暋慺悢偱寁嶼偟偨憹暆棪乿傒偨偄側傕偺偱偡丅
乽廃攇悢揱払娭悢乿傪乽揱払娭悢乿偲棯偟偰屇傇応崌傕偁傝丄乮杮彂偱傕傗偭偰偄傑偡乯娫堘偄偱偼偁傝傑偣傫偑丄杮棃偺堄枴偱偼彮偟堘偆傕偺偱偡丅乮崱偼堘偄偼偳偆偱傕偄偄偱偡乯
俇.侾. 楙廗
偡偱偵楙廗栤戣偱庢傝忋偘偨壓恾偺夞楬偺揱払娭悢傪媮傔偰偔偩偝偄丅
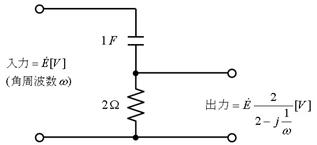
俇.俀. 摎
楙廗栤戣偺摎偐傜丄弌椡偼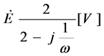 偲暘偭偰偄傑偡丅偦偙偱丄廃攇悢揱払娭悢偼壓恾偺傛偆偵弌椡傪擖椡偱妱偭偰丄寁嶼偱偒傑偡丅
偲暘偭偰偄傑偡丅偦偙偱丄廃攇悢揱払娭悢偼壓恾偺傛偆偵弌椡傪擖椡偱妱偭偰丄寁嶼偱偒傑偡丅
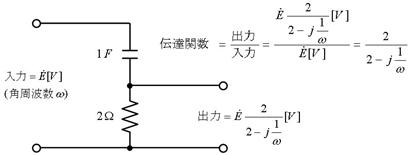
|
|
廃攇悢揱払娭悢
|
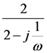
|
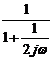 偲彂偔帠傕偱偒傑偡 偲彂偔帠傕偱偒傑偡
|
俇.俁. 楙廗
壓恾偺俠俼夞楬偺廃攇悢揱払娭悢傪壓昞傪杽傔側偑傜媮傔偰偔偩偝偄丅
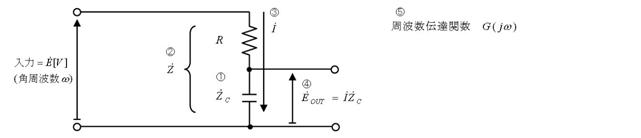
|
斣崋
|
幙栤
|
摎
|
|
嘆
|
僐儞僨儞僒偺廃攇悢冎偵偍偗傞丄暋慺僀儞僺乕僟儞僗偼
|
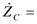
|
|
[兌]
|
|
嘇
|
擖椡偐傜尒傞偲俼俠偑捈楍側偺偱丄捈楍崌惉僀儞僺乕僟儞僗偼
|
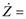
|
|
[兌]
|
|
嘊
|
俼俠偵棳傟傞揹棳偼擖椡揹埑俤傪僀儞僺乕僟儞僗偱妱偭偰丄
|
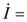
|
|
[俙]
|
|
嘋
|
弌椡揹埑偼丄棳傟傞揹棳偲僐儞僨儞僒偺僀儞僺乕僟儞僗傪妡偗偰
|
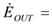
|
|
[倁]
|
|
嘍
|
揱払娭悢偼侾倁傪擖椡偟偨偲偒偺弌椡偩偐傜
|
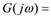
|
|
[攞]
|
俇.係. 摎
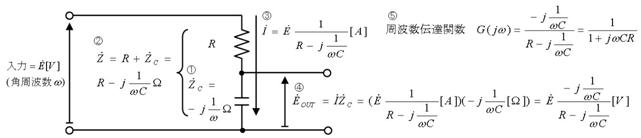
|
斣崋
|
幙栤
|
摎
|
|
嘆
|
僐儞僨儞僒偺廃攇悢冎偱偺暋慺僀儞僺乕僟儞僗偼
|
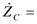
|
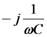
|
[兌]
|
|
嘇
|
擖椡偐傜尒傞偲丄俼俠偑捈楍側偺偱丄崌惉僀儞僺乕僟儞僗偼
|
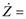
|
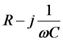
|
[兌]
|
|
嘊
|
偙偺偨傔丄俼俠偵棳傟傞揹棳偼擖椡揹埑傪僀儞僺乕僟儞僗偱妱偭偰丄
|
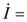
|
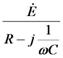
|
[俙]
|
|
嘋
|
弌椡揹埑偼丄揹棳偲僐儞僨儞僒偺僀儞僺乕僟儞僗傪妡偗偰
|
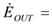
|
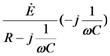
|
[倁]
|
|
嘍
|
揱払娭悢偼侾倁傪擖椡偟偨偲偒偺弌椡偩偐傜
|
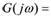
|
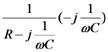
|
[攞]
|
|
|
悢妛偺摼堄側恖偼幃傪曄宍偟偰丄
乮嬯庤側恖偼曄宍偡傞昁梫偼偁傝傑偣傫丅曄宍偟側偔偰傕丄俤倶們倕倢偱寁嶼偱偒傑偡乯
|
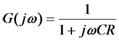
|
[攞]
|
俈. 廃攇悢揱払娭悢偺堄枴
揱払娭悢偼憹暆棪偺拠娫偱丄擖椡亊憹暆棪亖弌椡丄偱偁傞偺偲摨條偵丄擖椡亊揱払娭悢亖弌椡丄偲偄偆娭學偑偁傝傑偟偨丅
偱偡偐傜擖椡偑侾倁偺応崌傪峫偊傞偲丄侾亊憹暆棪亖弌椡丄侾亊揱払娭悢亖弌椡丄偮傑傝丄擖椡偑侾偺帪偺弌椡傪寁嶼偡傟偽丄偦傟偑揱払娭悢偱偡丅
偝偰摨偠帠傪暋慺揹埑偱峫偊傞偲丄壓恾偵帵偡偲偍傝丄揱払娭悢偑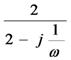 偺夞楬偵丄
偺夞楬偵丄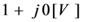 乮偮傑傝丄侾乯偺揹埑傪擖椡偡傞偲丄弌椡偼擖椡揹埑偲揱払娭悢傪妡偗偰丄
乮偮傑傝丄侾乯偺揹埑傪擖椡偡傞偲丄弌椡偼擖椡揹埑偲揱払娭悢傪妡偗偰丄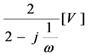 偲側傝丄摉慠側偑傜丄揱払娭悢偲慡偔摨偠偵側傝傑偡丅
偲側傝丄摉慠側偑傜丄揱払娭悢偲慡偔摨偠偵側傝傑偡丅
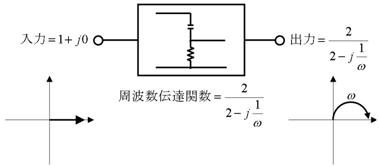
偮傑傝揱払娭悢偼丄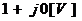 偺乮戝偒偝侾偱丄曃妏偑侽亱偺乯怣崋乮婎杮偺岎棳乯傪壛偊偨偲偒偺弌椡偲峫偊傞偙偲傕偱偒傑偡丅
偺乮戝偒偝侾偱丄曃妏偑侽亱偺乯怣崋乮婎杮偺岎棳乯傪壛偊偨偲偒偺弌椡偲峫偊傞偙偲傕偱偒傑偡丅
偱偡偐傜椺偊偽丄擖椡揹埑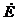 偐傜弌椡傪媮傔傞幃偑丄
偐傜弌椡傪媮傔傞幃偑丄
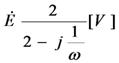
偲暘偭偰偄傞応崌偼丄廃攇悢揱払娭悢偲丄忋偺幃偺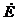 傪侾偵曄偊傞偩偗偱丄
傪侾偵曄偊傞偩偗偱丄
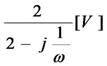
偲娙扨偵寁嶼偱偒傑偡丅
俉. 廃攇悢摿惈
揱払娭悢偼憹暆棪偺拠娫偱偡偐傜丄揱払娭悢偵娷傑傟傞妏廃攇悢乮冎乯傪條乆偵曄偊偰丄揱払娭悢偺戝偒偝乮愨懳抣乯傪寁嶼偡傟偽丄乽妏廃攇悢偺曄壔偵傛傞丄憹暆棪偺曄壔乿傪抦傞偙偲偑偱偒傑偡丅偙傟偑廃攇悢摿惈偱偡丅寁嶼偺曽朄偼弌椡揹埑偺寁嶼偲椙偔帡偰偄傑偡偑丄擖椡揹埑傪妡偗側偔偰傕椙偄偺偱懡彮娙扨偵側傝傑偡丅乮弌椡揹埑偺曄壔偱偼側偔丄憹暆棪偺曄壔傪寁嶼偡傞偐傜偱偡乯
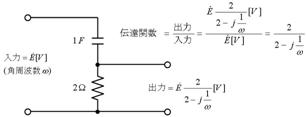
椺偊偽婛偵愢柧偟偨忋恾偺夞楬偺揱払娭悢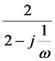 傪條乆側妏廃攇悢冎偱寁嶼偟丄偦偺幚晹丄嫊晹丄戝偒偝丄曃妏傪寁嶼偡傞僔乕僩傪嶌傞偲壓恾偺傛偆偵側傝傑偡丅
傪條乆側妏廃攇悢冎偱寁嶼偟丄偦偺幚晹丄嫊晹丄戝偒偝丄曃妏傪寁嶼偡傞僔乕僩傪嶌傞偲壓恾偺傛偆偵側傝傑偡丅

寁嶼寢壥偼壓恾偺傛偆偵側傝傑偡丅
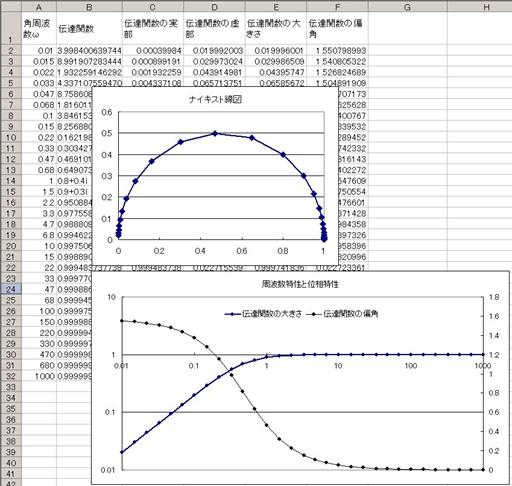
忋恾偱丄冎乮懳悢乯傪墶幉偵丄揱払娭悢偺戝偒偝乮懳悢乯傪僌儔僼偵偟偨傕偺偑乽廃攇悢摿惈乿丄冎乮懳悢乯傪墶幉偵丄揱払娭悢偺曃妏傪僌儔僼偵偟偨傕偺偑乽埵憡摿惈乿偱偡丅廃攇悢摿惈偲埵憡摿惈傪堦偮偺恾偵偐偄偰丄儃乕僨慄恾偲屇傇偙偲傕偁傝傑偡丅傑偨丄揱払娭悢偺幚晹偲嫊晹傪僌儔僼偵偟偨傕偺傪乽僫僀僉僗僩慄恾乿偲屇傃傑偡丅
揱払娭悢偐傜摼傜傟傞偙傟傜偺僌儔僼傪壓昞偵帵偟傑偡丅
|
墶幉
|
廲幉
|
昞偡撪梕
|
僌儔僼偺柤慜
|
|
妏廃攇悢冎乮懳悢乯
|
揱払娭悢偺愨懳抣
乮偍偍偒偝乯
乮懳悢乯
|
廃攇悢偺戝偒偝偵傛傞憹暆棪偺曄壔
|
廃攇悢摿惈
|
儃乕僨慄恾
|
|
妏廃攇悢冎乮懳悢乯
|
揱払娭悢偺曃妏
乮埵憡乯
乮懳悢乯
|
廃攇悢偺戝偒偝偵傛傞埵憡偺曄壔
|
埵憡摿惈
|
|
揱払娭悢偺幚晹
|
揱払娭悢偺嫊晹
|
憹暆棪偲埵憡偺娭學乮廃攇悢偼撉傒庢傝擄偄乯
|
僫僀僉僗僩慄恾
|
俋. 廃攇悢摿惈偲僨僔儀儖
僨乕僞僔乕僩摍偺帒椏偱偼丄揱払娭悢偺廃攇悢傪乮冎偱偼側偔乯俫倸偱巜掕偟丄寢壥偺愨懳抣傪棙摼倓俛偱丄曃妏傪乮儔僕傾儞偱偼側偔乯搙偱昞偡曽朄偑巊傢傟傑偡丅寁嶼偺曽朄偼摨偠偱丄扨埵傪曄偊偰寁嶼偡傞偩偗偱偡丅
偡偱偵愢柧偟偨壓恾偺夞楬偱丄廃攇悢俫倸偲倓俛丄搙傪巊偭偨廃攇悢丒埵憡摿惈恾乮儃乕僨慄恾乯傪俤倶們倕倢偱昤偒傑偡丅
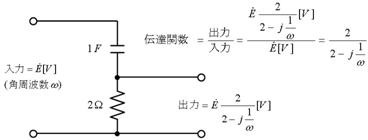
壓恾偺俤倶們倕倢僔乕僩偱偼丄梌偊偨廃攇悢偐傜妏廃攇悢冎傪媮傔丄偦偺冎偐傜揱払娭悢傪寁嶼偟偰丄偦偺寢壥傪倓俛偲搙偵曄姺偟偰昞帵偟偰偄傑偡丅
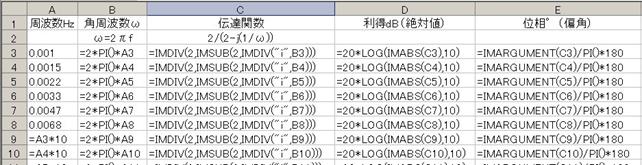
寁嶼偝偣丄僌儔僼傪昤偔偲壓恾偺傛偆偵側傝傑偡丅
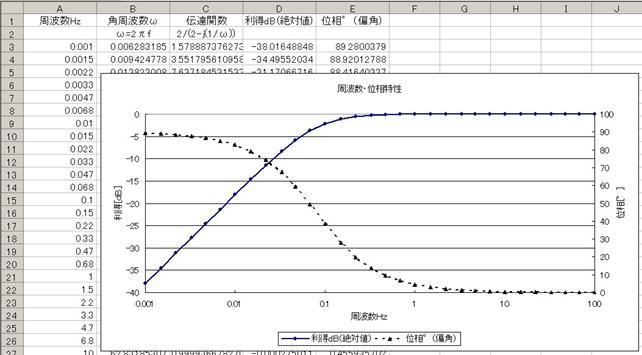
俋.侾. 楙廗
壓恾偺俠俼夞楬偺廃攇悢摿惈偺僌儔僼傪丄俤倶們倕倢傪巊偭偰昤偄偰偔偩偝偄丅墶幉偼廃攇悢俫倸偲偟丄廲幉偼棙摼倓俛偲偟偰偔偩偝偄丅
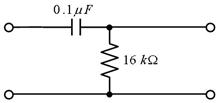
俋.俀. 摎
揱払娭悢偼丄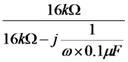 偙傟傪丄
偙傟傪丄
俤倶們倕倢偱偼=IMDIV(16E3,IMSUB(16E3,COMPLEX(0,-1/B2/0.1E-6)))偲擖椡偡傞偺偱丄壓婰偺傛偆偵俤倶們倕倧偵擖椡偟偰丄
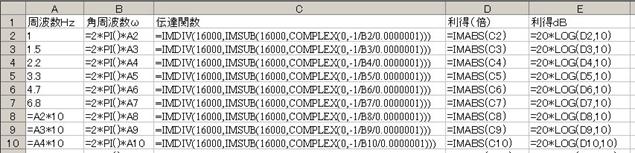
寁嶼偝偣丄僌儔僼傪昤偔偲壓恾偺傛偆偵昞帵偝傟傞丅
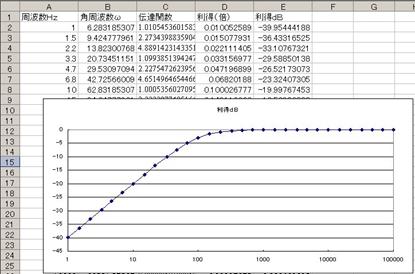
侾侽. 俠俼旝暘夞楬丒愊暘夞楬
壓恾嵍懁偑婛偵愢柧偟偨俠俼旝暘夞楬丄摨恾塃懁偑俠俼愊暘夞楬偱偡丅揱払娭悢偼偦傟偧傟恾偵帵偡捠傝偱偡丅
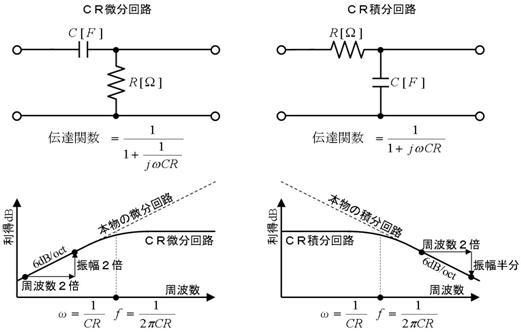
揱払娭悢傪尦偵廃攇悢摿惈乮棙摼乯傪昤偔偲忋恾偺傛偆偵側傝傑偡丅俠俼旝暘夞楬偼掅偄廃攇悢偱偼旝暘夞楬偲偟偰摥偒傑偡偑丄廃攇悢偑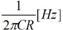 傛傝崅偔側傞偲丄暯傜側摿惈偵側偭偰偟傑偄傑偡丅
傛傝崅偔側傞偲丄暯傜側摿惈偵側偭偰偟傑偄傑偡丅
媡偵俠俼愊暘夞楬偼丄崅偄廃攇悢偱偼愊暘夞楬偲偟偰摥偒傑偡偑丄廃攇悢偑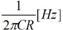 傛傝掅偔側傞偲丄暯傜側摿惈偵側偭偰偟傑偄傑偡丅
傛傝掅偔側傞偲丄暯傜側摿惈偵側偭偰偟傑偄傑偡丅
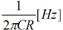 傛傝掅偄丄偁傞偄偼崅偄廃攇悢偱偼丄棙摼乮怣崋偺戝偒偝偑乯偑掅壓偟偰峴偔偺偱丄
傛傝掅偄丄偁傞偄偼崅偄廃攇悢偱偼丄棙摼乮怣崋偺戝偒偝偑乯偑掅壓偟偰峴偔偺偱丄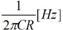 傪僇僢僩僆僼廃攇悢乮幷抐廃攇悢乯偲屇傫偱偄傑偡丅
傪僇僢僩僆僼廃攇悢乮幷抐廃攇悢乯偲屇傫偱偄傑偡丅
傑偨偄偢傟偺夞楬傕丄旝暘夞楬傗愊暘夞楬偲偟偰摥偔斖埻偱偼丄廃攇悢偑俀攞偵側傞偲怳暆偑俀攞丄偁傞偄偼敿暘偵側傝傑偡丅偙傟傪丄俇倓俛乛倧們倲乮俇僨僔儀儖僆僋僞乕僽乯偺摿惈偲屇傃傑偡丅
偮傑傝丄僆僋僞乕僽乮廃攇悢偑俀攞乯偵側傞偲丄怳暆偑亇俇倓俛乮怳暆偑俀攞丄偁傞偄偼敿暘偵乯憹尭偡傞偲偄偆帠偱偡丅
俇倓俛乛倧們倲偼丄俀侽倓俛乛倓倕們乮俀侽僨僔儀儖僨傿働乕僪乯偲傕屇偽傟傑偡丅廃攇悢偑侾侽攞偵側傞偲丄怳暆亇俀侽倓俛乮偮傑傝侾侽攞傗侾侽暘偺侾偵乯憹尭偡傞偲偄偆堄枴偱偡丅
侾侽.侾. 楙廗
壓恾偺俠俼夞楬偵偮偄偰丄壓昞偺栤偄偵摎偊偰偔偩偝偄丅
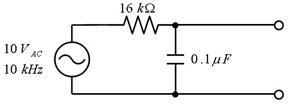
|
斣崋
|
幙栤
|
摎
|
|
嘆
|
夞楬偼俠俼旝暘夞楬偐丄愊暘夞楬偐
|
俠俼丂丂丂夞楬
|
|
嘇
|
僇僢僩僆僼廃攇悢偼丄
|
俫倸
|
|
嘊
|
怣崋廃攇悢偼僇僢僩僆僼廃攇悢偺壗攞偐丄
|
攞
|
|
嘋
|
怣崋偼壗暘偺侾偵庛傑傞偐丄
|
暘偺侾
|
|
嘍
|
弌椡怣崋偼壗倁俙俠偐丄
|
倣倁俙俠
|
侾侽.俀. 摎
僇僢僩僆僼廃攇悢偼壓恾偺捠傝寁嶼偟偰丄栺侾侽侽俫倸丄壛偊偰偄傞怣崋偼侾侽倠俫倸偱丄僇僢僩僆僼廃攇悢偺侾侽侽攞丄侾侽倠俫倸偼僇僢僩僆僼廃攇悢傛傝廫暘戝偒偄偺偱丄
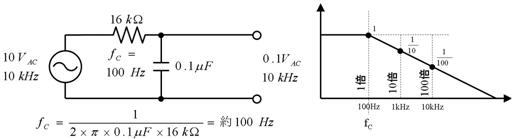
|
斣崋
|
幙栤
|
摎
|
|
嘆
|
夞楬偼俠俼旝暘夞楬偐丄愊暘夞楬偐
|
俠俼愊暘夞楬
|
|
嘇
|
僇僢僩僆僼廃攇悢偼丄
|
侾侽侽俫倸
|
|
嘊
|
怣崋廃攇悢偼僇僢僩僆僼廃攇悢偺壗攞偐丄
|
侾侽侽攞
|
|
嘋
|
怣崋偼壗暘偺侾偵庛傑傞偐丄
|
侾侽侽暘偺侾
|
|
嘍
|
弌椡怣崋偼壗倁俙俠偐丄
|
侾侽侽倣倁俙俠
|
侾侾. 妛栤揑側廃攇悢揱払娭悢
偙偙傑偱愢柧偟偨廃攇悢揱払娭悢偺僀儊乕僕偼丄壓恾嵍懁偺傛偆側傕偺偱偟偨丅偮傑傝乽妏廃攇悢冎傪梌偊傞偲丄偦偺廃攇悢偱偺弌椡偺戝偒偝偲埵憡偑暘傞乿偲偄偆棟夝偱偟偨丅

揹巕岺嶌偵偼偙偺峫偊曽偑岦偄偰偍傝丄棟夝偑娙扨側忋丄幚梡忋壗偺栤戣傕偁傝傑偣傫丅偨偩偟丄妛栤揑偵偼丄揱払娭悢偼乽倞冎傪梌偊傞偲丄偦偺廃攇悢偱偺弌椡偺戝偒偝偲埵憡偑暘傞乿偲峫偊傑偡丅偙偺傛偆偵峫偊傞偲丄悢妛偲偺宷偑傝偑椙偔側傞忋丄惂屼棟榑偵傕偡傫側傝擖傟傞乮惂屼棟榑偱偼倞冎偺強傪丄冃亄倞冎偵抲偒姺偊傞乯偨傔偱偡丅
偲偼偄偊丄妛栤偺峫偊曽偱傕丄揱払娭悢杮懱偵偼壗偺堘偄傕偁傝傑偣傫丅堘偄偼嵍懁傪俧乮冎乯偲偡傞偐丄俧乮倞冎乯偲偡傞偐丄偲偄偆揰偩偗偱偡丅
|
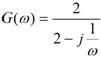
|
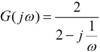
|
|
愢柧偟偨廃攇悢揱払娭悢
|
妛栤偺廃攇悢揱払娭悢
|
妛栤偺廃攇悢揱払娭悢偱偼丄幃偺拞偵乽j冎乿傪嶌傞偨傔偵曄宍偟丄偝傜偵乽俀乿傪堦売強偵偁偮傔偰丄
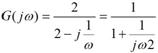
偲彂偔応崌偑杦偳偱偡丅傕偪傠傫丄杮彂偺栚揑偼丄悢妛偺旤偟偝傪姮擻偡傞帠偱偼偁傝傑偣傫偟丄傑偟偰傗幃偺曄宍傪楙廗偡傞偙偲偱偼偁傝傑偣傫偺偱丄偙偺曄宍偑偱偒傞昁梫偼偁傝傑偣傫丅偙傫側傕偺偼丄偦偺傑傑俤倶們倕倢偵擖傟偰寁嶼偱偒傟偽椙偄偺偱偡丅
侾俀. 乮嶲峫乯揱払娭悢偐傜乮巐懃墘嶼偩偗偱乯僗僥僢僾墳摎傪寁嶼偡傞
廃攇悢揱払娭悢偼丄廃攇悢偱怳暆傗埵憡偑偳偺傛偆偵曄壔偡傞偐傪昞偟偰偄傞偺偱丄岎棳埲奜偺攇宍乮偨偲偊偽丄撍慠億儞偲揹埑偑忋偑偭偨偲偒丗僗僥僢僾怣崋乯傪擖椡偟偨偲偒偺弌椡攇宍乮僗僥僢僾墳摎乯傪寁嶼偡傞偺偼嬯庤偱偡丅
偲偼偄偊丄俤倶們倕倢傪巊偭偰乮巐懃墘嶼偩偗偱乯偙偺傛偆側応崌偺弌椡傪寁嶼偡傞偙偲偼偱偒傑偡丅傕偪傠傫丄棷悢傗媡儔僾儔僗曄姺偼慡偔巊偄傑偣傫丅
偙偺傛偆偵丄揱払娭悢偐傜僗僥僢僾傪寁嶼偡傞帠偼偁傑傝偁傝傑偣傫偐傜丄堦椺傪徯夘偡傞偩偗偵棷傔傑偡丅俤倶們倕倢傪巊偊偽乽揱払娭悢偐傜巐懃墘嶼偩偗偱僗僥僢僾墳摎偑寁嶼偱偒傞傫偩乿偲偄偆帠偩偗抦偭偰偍偗偽椙偄偱偟傚偆丅
偝偰丄偨偲偊偽乽彫尛偄傪栣偆偨傃偵丄崱傑偱栣偭偨彫尛偄偺憤崌寁傪寁嶼偡傞乿偲尵偆姶偠偱丄乽偙傟傑偱偺抣偺崌寁乿傪媮傔傞寁嶼傪乽愊嶼乿偲屇傃傑偡丅偨偲偊偽丄侾丄俁丄俀偲棃傟偽丄愊嶼抣偼侾亄俁亄俀偱俇偱偡丅壓恾嵍懁偺僔乕僩偺俛楍偺抣偼丄俙楍傪愊嶼偟偨傕偺偱偡丅
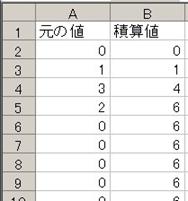 丂丂丂丂
丂丂丂丂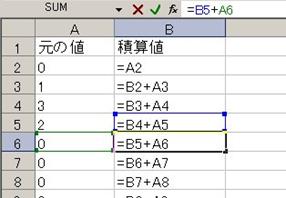
椺偊偽丄俛俆僙儖偺俇偼俙俀乣俙俆傑偱偺愊嶼抣偱偡丅愊嶼偺曽朄偼娙扨偱丄忋恾塃懁偺俛俇僙儖偵帵偡傛偆偵丄捈偖忋偺僙儖偲丄捈偖嵍偺僙儖傪懌偡偩偗偱偡丅乮幚偼偙偺乽懌偟嶼乿偮傑傝乽愊嶼乿偑丄乽愊暘乿側傫偱偡偗偳乧棟孅偼偝偰偍偄偰乯
師偵丄揱払娭悢偐傜擖椡倃偲弌椡倄偺娭學傪媮傔傑偡丅偡偱偵愢柧偟偨傛偆偵丄揱払娭悢偵擖椡揹埑傪妡偗傞偲弌椡揹埑偵側傝傑偟偨偐傜丄偨偲偊偽丄揱払娭悢
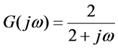
偱偼丄擖椡揹埑倃偲弌椡揹埑倄偺娭學偼丄
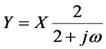
偱媮傔傞偙偲偑偱偒傑偡丅偙傟傪曄宍偟偰丄
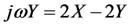 丂乧丂嘆
丂乧丂嘆
偲偟傑偡丅
偝偰偙偙偱丄偄偝偝偐晽曄傢傝側峫偊傪偟傑偡丅偮傑傝壓昞偺傛偆偵丄乽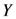 傪j冎偱妱傞偙偲偼丄俤倶們倕倢偱愊嶼偡傞偙偲偩乿偲峫偊傞偺偱偡丅
傪j冎偱妱傞偙偲偼丄俤倶們倕倢偱愊嶼偡傞偙偲偩乿偲峫偊傞偺偱偡丅
偄偝偝偐晽曄傢傝側峫偊曽偺昞
偨偲偊偽忋昞偱懢慄偱埻傫偩晹暘側傜丄乽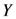 偼丄
偼丄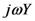 傪愊嶼偟偨傕偺偩乿偲峫偊傑偡丅偮傑傝丄
傪愊嶼偟偨傕偺偩乿偲峫偊傑偡丅偮傑傝丄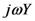 偼乽愊嶼偡傞慜偺弌椡
偼乽愊嶼偡傞慜偺弌椡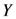 乿丄
乿丄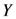 偼乽愊嶼偟偨屻偺弌椡
偼乽愊嶼偟偨屻偺弌椡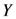 乿偱偡丅偙傟傪丄忋偺嘆幃偵斀塮偡傞偲丄
乿偱偡丅偙傟傪丄忋偺嘆幃偵斀塮偡傞偲丄
愊嶼偡傞慜偺弌椡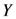 亖 俀亊擖椡
亖 俀亊擖椡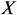 亅 俀亊愊嶼偟偨屻偺弌椡
亅 俀亊愊嶼偟偨屻偺弌椡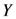 丂乧丂嘇
丂乧丂嘇
偲峫偊傞偙偲偑偱偒傞偺偱丄偦偺捠傝偵丄俤倶們倕倢偱丄壓恾偺傛偆側僔乕僩傪嶌惉偟傑偡丅
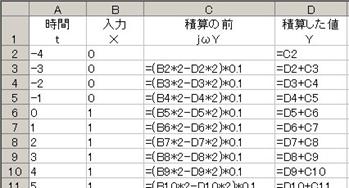
俠楍偺=(B*2-D2*2)*0.1摍偑忋偺嘇幃傪寁嶼偟偰偄傞晹暘偱丄枛旜偺乽*0.1乿偼丄寁嶼傪備偭偔傝峴偆偨傔偺傕偺偱偡乮抣偑彫偝偄偲抣偼備偭偔傝曄壔偟傑偡乯丅偙偺抣偼丄帪掕悢偺侾侽暘偺侾乣侾侽侽暘偺侾偑栚埨偱丄
帪掕悢偑0.1昩偺夞楬側傜*00.1掱搙偵愝掕偟傑偡丅乮偙偺抣偵傛偭偰侾峴偁偨傝偺帪娫偑寛傑傝傑偡乯
寁嶼偝偣偰丄僌儔僼傪昤偔偲壓恾偺傛偆偵僗僥僢僾墳摎偑昞帵偝傟傑偡丅
婎杮偺峫偊曽偼丄婛偵俠俼夞楬偱梡偄偨乽僔儈儏儗乕僔儑儞乿偲摨偠偱偡丅
偝傜偵暋嶨側揱払娭悢偱偼丄忋偺嘇幃傪嶌傞偲偒丄嵟傕愊嶼偺尮棳偵側偭偰偄傞崁丄偮傑傝乽偄偝偝偐晽曄傢傝側峫偊曽偺昞乿偱堦斣嵍偵偁傞傕偺乮倞冎偺師悢偑崅偄崁乯丄傪嵍曈乮嵍懁乯偵扨撈偱帩偭偰偔傞傛偆偵曄宍偡傞偺偑億僀儞僩偱偡丅俤倶們倕倢偱偼丄崱夞偺俠楍偵憡摉偡傞丄嵍曈偺抣傪帵偡楍偑寁嶼偺拞怱偵側傝傑偡丅偙偺楍偵擖椡揹埑傗愊嶼抣傪尦偵嵍曈偺抣傪媮傔傞幃傪婰擖偟傑偡丅揱払娭悢偵傛偭偰偼丄愊嶼偟偨抣傪愊嶼偟偨抣偺楍丄愊嶼偟偨抣傪愊嶼偟偨抣傪愊嶼偟偨抣偺楍丄傪嶌傞応崌傕偁傝傑偡丅
侾. 僆儁傾儞僾
僆儁傾儞僾偼戲嶳偺慺巕傪撪憼偡傞偙偲偱丄傎傏棟憐揑側惈擻傪帩偨偣偨敿摫懱晹昳偱偡丅棟憐揑側暘丄暼偑柍偔偰愝寁傕娙扨偱偡丅
搊応偟偨摉弶偼抣抜偑崅偔偰丄儂僀儂僀偲巊偆偙偲偼弌棃傑偣傫偱偟偨丅偟偐偟丄尰嵼偼係偮擖傝俀俆墌側偳偲埨壙偵斕攧偝傟偰偍傝丄搾悈偺傛偆偵巊偆偙偲偑偱偒傑偡丅
乽棟憐揑側惈擻乿偲偼尵偭偰傕丄懡彮偼乽棟憐偵撏偐側偄晹暘乿傕偁傝傑偡丅偦偙偱僆儁傾儞僾夞楬偺愝寁偼丄傑偢丄乽棟憐揑側惈擻乿乮棟憐僆儁傾儞僾乯偲峫偊偰愝寁偟丄偦偺屻偱乽棟憐偵撏偐側偄晹暘乿偵傛傞埆塭嬁傪専摙偡傞応崌偑懡偄偱偡丅
偙偙偱偼傑偢乽棟憐揑側惈擻乿偲峫偊偰愝寁偡傞曽朄傪愢柧偟傑偡丅崱擔偺僆儁傾儞僾偼惈擻偑岦忋偟偰偄傞偺偱丄偙偺傛偆側愝寁偱傕丄偦偺傑傑巊偊傞応崌偑憡摉偁傝傑偡丅
偲傝傢偗丄儗僀儖丒僩僂丒儗僀儖擖弌椡偑壜擻側丄弌椡揹棳偺斾妑揑戝偒側俠俷俵俽僆儁傾儞僾傪巊偊偽丄廃攇悢偺掅偄夞楬側傜丄乽棟憐揑側惈擻乿偲峫偊偰愝寁偟偰傕丄奣偹惓偟偔摦嶌偟傑偡丅僆儁傾儞僾偺婎杮偩偗傪棟夝偟偨抜奒偱傕乮懡彮妱崅偱偡偑乯偙偺傛偆側僆儁傾儞僾乮椺偊偽丄俶俰俵俈侽係係乮俀倁乣俆倁揹尮梡乯傗丄俴俵俠俇係俉係乮俆乣侾俆倁揹尮梡乯乯傪巊偊偽愝寁傪妝偟傓偙偲偑偱偒傞偱偟傚偆丅偦偟偰丄杮彂偺愢柧偑奣偹棟夝偱偒傟偽丄栚揑偵墳偠偰妱埨側僆儁傾儞僾傪慖傇偙偲傕廫暘妝偟傔傞偱偟傚偆丅
俀. 僆儁傾儞僾偺抂巕偲摦嶌
壓恾偵帵偡傛偆偵丄僆儁傾儞僾偵偼乽亄擖椡抂巕乿乽亅擖椡抂巕乿乽弌椡抂巕乿乮偙偙偱偼乽亄擖椡乿乽亅擖椡乿乽弌椡乿偲棯偟傑偡乯偺俁杮偺怣崋抂巕偲丄乽亄揹尮抂巕乿乽亅揹尮抂巕乿乮偙偙偱偼乽亄揹尮乿乽亅揹尮乿偲棯偟傑偡乯偺俀杮偺揹尮抂巕偑偁傝傑偡丅
俀杮偺揹尮抂巕偼夞楬恾偱偼偟偽偟偽徣棯偝傟傑偡丅
僆儁傾儞僾 偼-亄擖椡偲-亅擖椡-偺揹埑偺乽嵎乿傪媮傔偰丄偙傟傪廫暘偵憹暆偟偰-弌椡-偵弌偟傑偡丅偮傑傝丄
弌椡丂亖
乮丂亄擖椡丂亅丂亅擖椡丂乯亊丂戝偒側憹暆棪
仸乽戝偒側憹暆棪乿偼椺偊偽侾侽枩攞摍偱偡
偦偟偰丄堷偒嶼偑惓妋偱丄憹暆棪偑戝偒偄偺偱丄師偺崁偱愢柧偡傞係偮偺惈幙偑惗偠傑偡丅
俁. 棟憐揑側僆儁傾儞僾偺惈幙
僆儁傾儞僾偺惈幙偼戲嶳偁傝傑偡偑丄壓昞偺係偮傪棟夝偡傟偽丄俋妱偺婎杮夞楬偼棟夝偡傞偙偲偑偱偒傑偡丅
傑偢丄僆儁傾儞僾偼乽惓妋乿偱乽戝偒側憹暆棪乿偺晹昳偱偡偐傜丄壓昞偺斣崋嘇偲嘊偵帵偡傛偆偵丄亄擖椡偺揹埑偑丄嬐偐偱傕亅擖椡傛傝崅偄偩偗偱丄弌椡偼亄揹尮揹埑傑偱價儏儞偲怳傝愗偭偰偟傑偄傑偡丅摨條偵丄亄擖椡偺揹埑偑丄嬐偐偱傕亅擖椡傛傝掅偄偩偗偱丄弌椡偼亅揹尮揹埑傑偱價儏儞偲怳傝愗偭偰偟傑偄傑偡丅
師偵丄憹暆棪偑戝偒偄偨傔丄壓昞嘆偵帵偡傛偆偵丄亄擖椡偑亅擖椡偲慡偔摨偠帪偩偗乽弌椡偑怳傝愗傜側偄乿忬懺偵側傝傑偡丅媡偵丄弌椡偑怳傝愗偭偰側偗傟偽丄亄擖椡偲亅擖椡偼摨偠揹埑偱偁傞偲傕尵偊傑偡丅
偙偙偱婥傪偮偗傞偙偲偼丄偙偺傛偆側乮嘆偺乯乽怳傝愗傜側偄乿忬懺偲側傞偺偼丄夞楬峔惉偑丄晧婣娨偺乮弌椡抂巕偺揹埑偑擖椡抂巕偵夞傝崬傫偱偄傞乯応崌偩偗偱丄偦傟埲奜偺夞楬偱偼乮嘇偲嘊偺乯怳傝愗偭偨忬懺偱摦嶌偡傞偲偄偆揰偱偡丅偮傑傝丄怳傝愗偭偰嘇嘊偺摦嶌傪偡傞偐丄怳傝愗傜偢偵嘆偺摦嶌傪偡傞偐偼丄夞楬峔惉偱寛傑傞偲峫偊偰偔偩偝偄丅乮棟桼偼屻偱愢柧偟傑偡乯
僆儁傾儞僾夞楬偺廳梫側惈幙
|
斣崋
|
擖椡抂巕偺忬懺
|
|
弌椡抂巕偺忬懺
|
夞楬偺峔惉
|
|
嘆
|
亄擖椡 亖 亅擖椡
|
佁
|
怳傝愗傜側偄
|
晧婣娨偺夞楬
乮弌椡抂巕偺揹埑偑丄擖椡抂巕偵夞傝崬傫偱偄傞乯
|
|
嘇
|
亄擖椡 亜 亅擖椡
|
佁
|
亄偵怳傝愗傞
|
晧婣娨偱側偄夞楬
乮弌椡抂巕偺揹埑偑丄擖椡抂巕偵夞傝崬傫偱偄側偄乯
|
|
嘊
|
亄擖椡 亙 亅擖椡
|
佁
|
亅偵怳傝愗傞
|
|
嘋
|
擖椡抂巕偵偼揹棳偑棳傟側偄
|
嵟屻偵丄忋昞偺嘆乣嘊偺壗傟偺応崌偱傕丄摨昞嘋偵帵偡傛偆偵擖椡抂巕偵偼揹棳偑棳傟傑偣傫丅
偱偡偐傜丄僆儁傾儞僾偺夞楬傪撉傓偲偒偼丄晧婣娨偺桳柍傪嵟弶偵敾掕偟偰丄師昞偺傛偆偵峫偊傑偡丅
|
夞楬峔惉
|
棙梡偡傞摿挜
|
|
晧婣娨偑妡偐偭偰偄傞
|
嘆偲嘋偺惈幙偱峫偊傞
|
|
晧婣娨偼側偄
|
嘇偲嘊偲嘋偺惈幙偱峫偊傞
|
係. 儐僯僥傿僎僀儞憹暆婍
偱偼丄廳梫側係偮偺惈幙傪巊偭偰僆儁傾儞僾偺夞楬傪撉傒傑偡丅
嵟弶偵庢傝忋偘傞乽儐僯僥傿僎僀儞憹暆婍乮儐僯僥傿僎僀儞僶僢僼傽偲傕屇偽傟傑偡乯乿偼丄婏柇側柤慜偱偡偑乽侾攞偺憹暆婍乿偲偄偆堄枴偱偡丅偮傑傝丄擖傟偨揹埑偑偦偺傑傑弌偰偔傞憹暆婍偱偡偐傜丄堦尒栶偵棫偨側偄傛偆偵巚偊傑偡丅
偟偐偟丄廳梫側惈幙嘋偵傛傝丄擖椡抂巕偵偼揹棳偑棳傟傑偣傫偐傜丄偨偲偊偽丄儐僯僥傿僎僀儞憹暆婍偱丄廩揹偟偨僐儞僨儞僒偺揹埑傪應掕偟偰傕丄僐儞僨儞僒偑曻揹偟偰揹埑偑掅壓偡傞偙偲偑偁傝傑偣傫丅偮傑傝丄儐僯僥傿僎僀儞憹暆婍傪巊偆偲丄應掕偝傟傞夞楬偵塭嬁傪梌偊偢偵丄惓妋偵揹埑傪應掕偱偒傞偺偱偡丅
憹暆婍偺傛偆側丄擖椡揹埑偺戝彫偱丄弌椡揹埑傕妸傜偐偵曄壔偡傞夞楬偼丄乮僆儁傾儞僾傪巊偭偨応崌乯偐側傜偢晧婣娨偺妡偐偭偨夞楬偱偡丅
偝偰丄壓恾偑儐僯僥傿僎僀儞憹暆婍偺椺偱偡丅嵍偐傜揹埑傪梌偊傞偲丄塃懁偵弌椡偟傑偡丅
壓恾偵奃怓栴報偱帵偡傛偆偵丄弌椡抂巕偺揹埑偑亅擖椡偵夞傝崬傫偱偄傑偡偐傜丄晧婣娨偺夞楬偱偡丅偱偡偐傜丄廳梫側惈幙偺嘆偲嘋傪巊偭偰峫偊傑偡丅
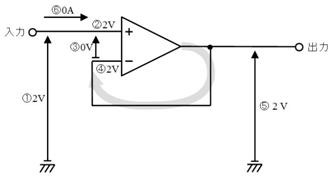
係.侾. 妋擣
忋恾傪尒偰壓昞偵彂偒崬傒側偑傜儐僯僥傿僎僀儞憹暆婍偺摦嶌傪妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡揹埑偼丄
|
倁
|
|
嘇
|
亄擖椡抂巕偺揹埑偼丄
|
倁
|
|
嘊
|
廳梫側惈幙嘆偵傛傟偽丄乮晧婣娨偺夞楬偱偼乯俀杮偺擖椡抂巕偺揹埑嵎偼
|
倁
|
|
嘋
|
亅擖椡抂巕偺揹埑偼丄
|
倁
|
|
嘍
|
弌椡揹埑偼丄
|
倁
|
|
嘐
|
廳梫側惈幙嘋偵傛傟偽丄擖椡偵棳傟傞揹棳偼丄
|
俙
|
係.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡揹埑偼丄
|
俀倁
|
|
嘇
|
亄擖椡抂巕偺揹埑偼丄
|
俀倁
|
|
嘊
|
廳梫側惈幙嘆偵傛傟偽丄乮晧婣娨偺夞楬偱偼乯俀杮偺擖椡抂巕偺揹埑嵎偼
|
侽倁
|
|
嘋
|
亅擖椡抂巕偺揹埑偼丄
|
俀倁
|
|
嘍
|
弌椡揹埑偼丄
|
俀倁
|
|
嘐
|
廳梫側惈幙嘋偵傛傟偽丄擖椡偵棳傟傞揹棳偼丄
|
侽俙
|
忋昞偺嘍偱暘傞傛偆偵丄擖椡偟偨揹埑偑偦偺傑傑弌椡偝傟傑偡丅傑偨丄忋昞偺嘐偱暘傞傛偆偵擖椡偵偼揹棳偑棳傟傑偣傫丅
俆. 僆儁傾儞僾偺揹尮
乽揹尮乿偲偼夞楬恾偵揹抮偺恾婰崋偱帵偡傛偆側丄夞楬傪摦嶌偝偣傞僄僱儖僊傪嫙媼偡傞晹暘偺偙偲偱偡丅
尦棃僆儁傾儞僾偼丄壓恾嵍懁偵帵偡傛偆偵丄亄揹尮偲亅揹尮偺俀揹尮乮椉揹尮乯偱巊梡偡傞傛偆偵愝寁偝傟傑偟偨丅側偤側傜丄亄揹尮偲亅揹尮偺恀傫拞偁偨傝乮偮傑傝丄侽倁晅嬤乯偱埨掕偟偰摦嶌偡傞偐傜偱偡丅
偲偙傠偑丄僆儁傾儞僾偺墳梡斖埻偑峀偑傞偵偮傟丄揹尮傪侾偮偟偐搵嵹偟側偄傛偆側丄寉曋側婡婍偱傕棙梡偝傟傞傛偆偵側傝丄壓恾塃懁偵帵偡傛偆側丄扨堦揹尮偱巊梡偝傟傞婡夛偑憹偊偰棃傑偟偨丅
摉弶偼丄俀揹尮梡偵愝寁偝傟偨僆儁傾儞僾傪丄夞楬傪岺晇偟偰扨堦揹尮偱巊梡偟偰偄傑偟偨偑丄偦偺屻丄扨堦揹尮梡偺僆儁傾儞僾傕嶌傜傟傞傛偆偵側傝傑偟偨丅
夞楬偺摦嶌偼俀揹尮偺曽偑愢柧偟堈偄応崌偑懡偄偺偱丄杮彂偱偼摿偵揹尮傪帵偝側偄尷傝丄俀揹尮偲峫偊偰愢柧偟偰偄傑偡丅
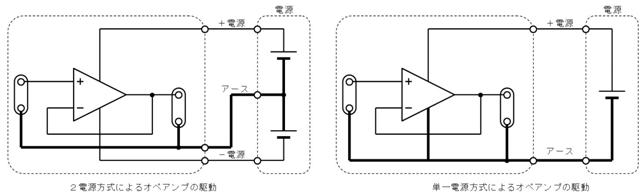
俇. 僆儁傾儞僾偺拞偺恖
偝偰丄儐僯僥傿僎僀儞憹暆婍偺摥偒偼丄廳梫側惈幙嘆乽晧婣娨偺夞楬側傜丄亄擖椡亖亅擖椡乿傪丄棙梡偟偰峫偊傑偟偨丅偙偙偱偼丄僆儁傾儞僾傪媅恖壔偡傞偙偲偱丄側偤偙偺廳梫側惈幙嘆偑惗偠傞偺偐愢柧偟傑偡丅壓恾偑媅恖壔偟偨僆儁傾儞僾偱偡丅
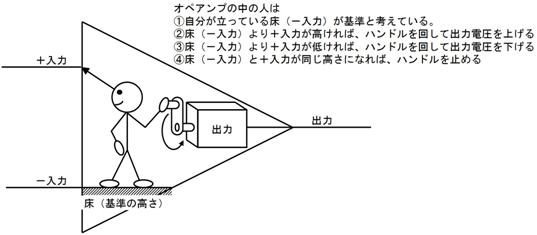
僆儁傾儞僾偺拞偺恖偼丄忋恾偺傛偆偵乽乮帺暘偑棫偮乯彴乮亅擖椡乯偑婎弨乿偲峫偊偰偄傑偡丅偦偟偰丄忢偵亄擖椡偺揹埑傪婥偵偟偰偄傑偡丅
拞偺恖偼丄亄擖椡偺揹埑偑丄彴乮亅擖椡乯傛傝崅偗傟偽丄僴儞僪儖傪夞偟偰弌椡傪忋偘傑偡丅媡偵丄亄擖椡偑丄彴乮亅擖椡乯傛傝掅偗傟偽丄媡偵僴儞僪儖傪夞偟偰弌椡揹埑傪壓偘傑偡丅
拞偺恖偼丄彴偲亄擖椡偺揹埑偵堘偄偑偁傞尷傝丄僴儞僪儖偼偄偮傑偱傕夞偟懕偗傑偡丅偟偐偟丄弌椡揹埑偑揹尮抂巕偺揹埑偵払偡傞偲丄乮揹尮揹埑傪墇偊傞揹埑偼弌椡偱偒傑偣傫偐傜乯偦傟埲忋僴儞僪儖偼夞傜側偔側傝傑偡丅乮偙傟偑屻偱愢柧偡傞僐儞僷儗乕僞偺摦嶌偱偡乯
偝偰丄壓恾偼媅恖壔偟偨儐僯僥傿僎僀儞憹暆婍偱偡丅
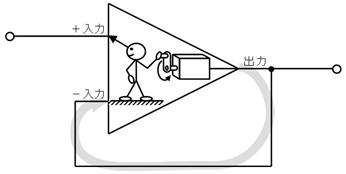
忋恾偺夞楬偱偼丄弌椡揹埑偑亅擖椡偵夞傝崬傫偱晧婣娨偑妡偐偭偰偄傑偡丅偙偺傛偆偵晧婣娨偵愙懕偟偨偙偲偱丄寑揑側曄壔偑婲偒傑偡丅偮傑傝丄拞偺恖偑乽僴儞僪儖傪夞偟偰丄帺暘偺彴偺崅偝傪忋壓偱偒傞乿傛偆偵側傞偺偱偡丅
偙偺偨傔拞偺恖偼丄亄擖椡偑彴傛傝崅偗傟偽丄僴儞僪儖傪夞偟偰彴傪忋偘偰峴偒傑偡丅偦偟偰丄彴偺崅偝偑亄擖椡偲摨偠偵側傟偽丄僴儞僪儖傪夞偡偺傪巭傔傑偡丅偦偺寢壥丄弌椡揹埑乮亅擖椡乯偑亄擖椡偲摍偟偔側傞偺偱偡丅
偮傑傝晧婣娨傪妡偗傞偙偲偱丄拞偺恖偑乽帺暘偑棫偮彴偺崅偝傪曄偊傞乿偙偲傪壜擻偵偟丄偦偺寢壥拞偺恖偑亄擖椡偲摨偠崅偝傑偱彴傪忋偘傞乮壓偘傞乯偨傔偵丄僆儁傾儞僾偺廳梫側惈幙嘆丄偮傑傝乽亄擖椡亖亅擖椡乮彴乯乿偑惗傑傟傞偺偱偡丅
傑偨丄拞偺恖偼僴儞僪儖傪夞偟偰揹埑傪忋偘壓偘偟傑偡偐傜丄幚偼弌椡揹埑偼弖帪偵忋壓偱偒傑偣傫丅偙偺偨傔丄儐僯僥傿僎僀儞憹暆婍偵戝偒側怳暆偺怣崋傪擖傟傞偲丄壓恾偺壓懁偵帵偡傛偆偵丄揹埑偑彊乆偵曄壔偟傑偡丅乮屻偵徻偟偔愢柧偟傑偡乯偙傟傕幚嵺偺僆儁傾儞僾偱惗偠傞乮僗儖乕儗乕僩偲尵偆乯尰徾偱偡丅
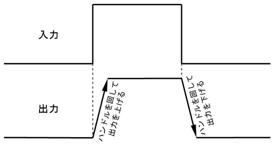
俉. 旕斀揮憹暆夞楬
偙偙偱庢傝忋偘傞乽旕斀揮憹暆夞楬乿偼曄側柤慜偱偡偑乽斀揮偟側偄憹暆婍乿偮傑傝丄乽擖椡偑亄偵怳傟偨傜丄弌椡傕亄偵怗傟傞乿偲偄偆乽偁傝偒偨傝偺乿憹暆婍偱偡丅乮僆儁傾儞僾憹暆婍偱偼丄擖弌椡偑斀揮偡傞応崌偑庡棳側偺偱丄偁偊偰乽旕斀揮乿偲庡挘偟偰偄傞栿偱偡乯
旕斀揮憹暆婍偼丄儐僯僥傿僎僀儞憹暆婍偲偪偑偄丄擖椡偝傟偨揹埑傪戝偒偔偡傞嶌梡偑偁傝傑偡丅
壓恾偑旕斀揮憹暆夞楬偺椺偱丄嵍偐傜揹埑傪梌偊傞偲丄塃懁偵弌椡偟傑偡丅
偙偺夞楬偼壓恾奃怓栴報偱帵偡傛偆偵丄弌椡抂巕偺揹埑偑亅擖椡偵夞傝崬傫偱偄傑偡偐傜丄晧婣娨偺夞楬偱偡丅偱偡偐傜丄廳梫側惈幙偺嘆偲嘋傪巊偭偰峫偊傑偡丅
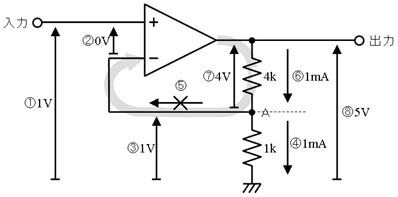
俉.侾. 妋擣
忋恾傪尒偰壓昞偵彂偒崬傒側偑傜旕斀揮憹暆夞楬偺摦嶌傪妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偵壛傢傞揹埑偼
|
倁
|
|
嘇
|
廳梫側惈幙嘆偵傛傟偽丄俀杮偺擖椡抂巕偺揹埑嵎偼
|
倁
|
|
嘊
|
亅擖椡抂巕偺揹埑偼
|
倁
|
|
嘋
|
侾倠兌偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘍
|
廳梫側惈幙嘋偵傛傟偽丄侾倠兌偺忋懁偐傜丄亅擖椡抂巕偵岦偐偭偰棳傟傞揹棳偼丄
|
倣俙
|
|
嘐
|
係倠兌偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘑
|
係倠兌偵惗偠傞揹埑乮椉抂揹埑乯偼丄
|
倁
|
|
嘒
|
弌椡抂巕偺揹埑偼丄
|
倁
|
俉.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偵壛傢傞揹埑偼
|
侾倁
|
|
嘇
|
廳梫側惈幙嘆偵傛傟偽丄俀杮偺擖椡抂巕偺揹埑嵎偼
亄擖椡 亖 亅擖椡偱偁傞偐傜丄
|
侽倁
|
|
嘊
|
亅擖椡抂巕偺揹埑偼丄亄擖椡偲摨偠偱偁傞偐傜丄
|
侾倁
|
|
嘋
|
侾倠兌偵棳傟傞揹棳偼丄侾倁偱侾倠兌偱偁傞偐傜丄
|
侾倣俙
|
|
嘍
|
廳梫側惈幙嘋偵傛傟偽丄侾倠兌偺忋懁偐傜丄亅擖椡抂巕偵岦偐偭偰棳傟傞揹棳偼丄擖椡抂巕偵偼揹棳偑棳傟側偄偐傜丄
|
侽倣俙
|
|
嘐
|
係倠兌偵棳傟傞揹棳偼丄僉儖僸儂僢僼偺朄懃傪俙揰偵巊偭偰丄
|
侾倣俙
|
|
嘑
|
係倠兌偵惗偠傞揹埑乮椉抂揹埑乯偼丄
|
係倁
|
|
嘒
|
弌椡抂巕偺揹埑偼丄侾倁偲係倁傪壛偊偰
|
俆倁
|
偮傑傝丄偙偺夞楬偼侾倁傪擖傟傞偲俆倁傪弌椡偟傑偡丅俆攞偵憹暆偟偰偄傞傛偆偱偡丅偟偐偟丄傂傚偭偲偡傞偲忢偵俆倁弌椡偝傟偰丄幚偼憹暆偼偝傟偰偄側偄偺偐傕抦傟傑偣傫丅偦偙偱丄擖椡傪俀倁偵曄峏偟偰丄傕偆堦搙専摙偟傑偡丅
俉.俁. 楙廗
壓恾偺夞楬恾偺奺晹偺揹埑丒揹棳傪壓昞偵婰擖偟偰偔偩偝偄丅傑偨丄憹暆婍偺擖椡揹埑偲弌椡揹埑偺娭學乮擖弌椡揹埑摿惈乯傪壓恾塃懁偺僌儔僼偵彂偒崬傫偱偔偩偝偄丅
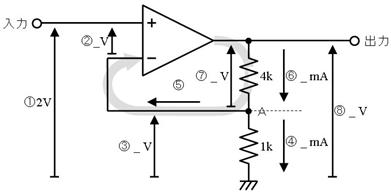
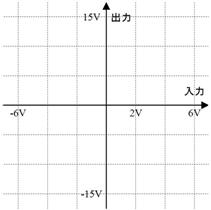
忋恾傪尒偰壓昞偵彂偒崬傒側偑傜峫偊偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偵壛傢傞揹埑偼
|
倁
|
|
嘇
|
廳梫側惈幙嘆偵傛傟偽丄俀杮偺擖椡抂巕偺揹埑嵎偼
|
倁
|
|
嘊
|
亅擖椡抂巕偺揹埑偼
|
倁
|
|
嘋
|
侾倠兌偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘍
|
廳梫側惈幙嘋偵傛傟偽丄侾倠兌偺忋懁偐傜丄亅擖椡抂巕偵岦偐偭偰棳傟傞揹棳偼丄
|
倣俙
|
|
嘐
|
係倠兌偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘑
|
係倠兌偵惗偠傞揹埑乮椉抂揹埑乯偼丄
|
倁
|
|
嘒
|
弌椡抂巕偺揹埑偼丄
|
倁
|
俉.係. 摎
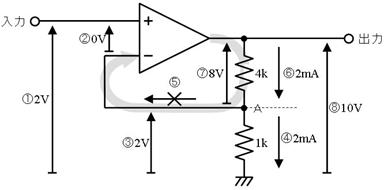
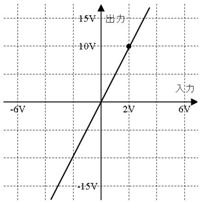
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偵壛傢傞揹埑偼
|
俀倁
|
|
嘇
|
廳梫側惈幙嘆偵傛傟偽丄俀杮偺擖椡抂巕偺揹埑嵎偼
亄擖椡 亖 亅擖椡偱偁傞偐傜丄
|
侽倁
|
|
嘊
|
亅擖椡抂巕偺揹埑偼丄亄擖椡偲摨偠偱偁傞偐傜丄
|
俀倁
|
|
嘋
|
侾倠兌偵棳傟傞揹棳偼丄侾倁偱侾倠兌偱偁傞偐傜丄
|
俀倣俙
|
|
嘍
|
廳梫側惈幙嘋偵傛傟偽丄侾倠兌偺忋懁偐傜丄亅擖椡抂巕偵岦偐偭偰棳傟傞揹棳偼丄擖椡抂巕偵偼揹棳偑棳傟側偄偐傜丄
|
侽倣俙
|
|
嘐
|
係倠兌偵棳傟傞揹棳偼丄僉儖僸儂僢僼偺朄懃傪俙揰偵巊偭偰丄
|
俀倣俙
|
|
嘑
|
係倠兌偵惗偠傞揹埑乮椉抂揹埑乯偼丄
|
俉倁
|
|
嘒
|
弌椡抂巕偺揹埑偼丄侾倁偲係倁傪壛偊偰
|
侾侽倁
|
侾倁傪擖椡偡傞偲俆倁傪丄俀倁傪擖椡偡傞偲侾侽倁傪弌椡偟偰偄傑偡偐傜丄柧傜偐偵侾侽攞偵憹暆偟偰偄傑偡丅擖椡偲弌椡偺娭學傪忋恾塃懁偺僌儔僼偵帵偟傑偡丅
偙偺憹暆婍偺揹埑憹暆棪俙倁偼丄俀杮偺掞峈偐傜師偺傛偆偵寁嶼偱偒傑偡丅
揹埑憹暆棪俙倁亖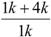 亖俆攞
亖俆攞
旕斀揮憹暆夞楬偼丄儐僯僥傿僎僀儞憹暆婍偲摨條丄亄擖椡抂巕偑偦偺傑傑憹暆婍偺擖椡抂巕偵側偭偰偄傑偡偐傜丄廳梫側惈幙嘋偵傛傝丄擖椡偵揹棳偑棳傟傑偣傫丅
俉.俆. 楙廗
壓恾偺憹暆夞楬偺奺晹偺揹埑丒揹棳偲丄揹埑憹暆棪傪媮傔偰偔偩偝偄丅傑偨丄憹暆婍偺擖椡揹埑偲弌椡揹埑偺娭學乮擖弌椡揹埑摿惈乯傪壓恾塃懁偺僌儔僼偵彂偒崬傫偱偔偩偝偄丅
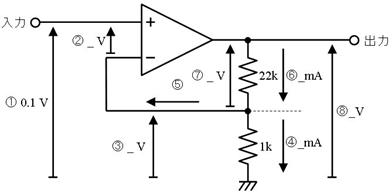
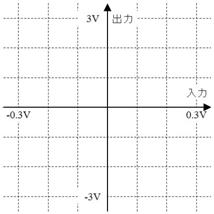
|
嘆丂丂 丂丂丂倁
|
嘇丂丂丂丂丂丂倁
|
嘊丂丂丂丂丂丂倁
|
嘋丂丂丂丂丂倣俙
|
|
嘍丂丂 丂丂倣俙
|
嘐丂丂丂丂丂倣俙
|
嘑丂丂丂丂丂丂倁
|
嘒丂丂丂丂丂丂倁
|
|
嘓俙倁 亖 丂丂攞
|
|
|
|
俉.俇. 摎
壓恾奃怓偺宱楬偱晧婣娨偑妡偐偭偰偄傞偺偱丄廳梫側惈幙嘆偲嘋傪巊偄傑偡丅
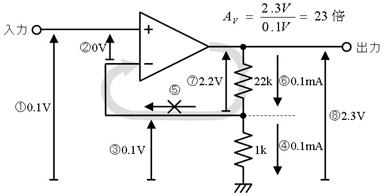
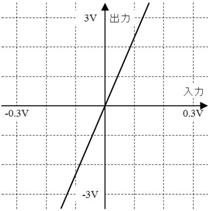
|
嘆丂丂 侽丏侾倁
|
嘇丂丂丂丂丂侽倁
|
嘊丂丂丂侽丏侾倁
|
嘋丂丂侽丏侾倣俙
|
|
嘍丂丂 丂侽倣俙
|
嘐丂丂侽丏侾倣俙
|
嘑丂丂丂俀丏俀倁
|
嘒丂丂丂俀丏俁倁
|
|
嘓俙倁 亖 俀俁攞
|
|
|
|
俋. 僐儞僷儗乕僞
僐儞僷儗乕僞偼乽斾傋傞夞楬乿偲偄偆堄枴偱乽斾妑夞楬乿偲栿偝傟偰偄傑偡丅擖椡揹埑偑偁傞揹埑傛傝乽崅偄偐乿乽掅偄偐乿傪敾暿偡傞摥偒偑偁傝傑偡丅偙偺傛偆側弌椡偺忬懺偑乽僀僠偐僶僠偐乿偲偄偆夞楬偼丄晧婣娨偺妡偐偭偰側偄夞楬偱偡丅偱偡偐傜丄廳梫側惈幙偺嘇嘊嘋傪巊偭偰峫偊傑偡丅
壓恾偵僐儞僷儗乕僞偺椺傪帵偟傑偡丅乮偙偙偱偼丄俆倁偺扨堦揹尮偱峫偊偰偄傑偡乯
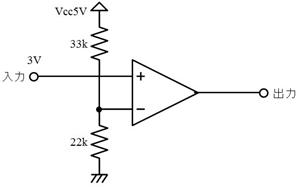
俋.侾. 楙廗
忋恾傪尒偰壓昞偵彂偒崬傒側偑傜峫偊偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
暘埑偺朄懃偱丄俀俀倠偺椉抂揹埑偼丄
|
倁
|
|
嘇
|
亅擖椡抂巕偺揹埑偼丄
|
倁
|
|
嘊
|
亄擖椡抂巕偺揹埑偼丄
|
倁
|
|
嘋
|
亄擖椡偲亅擖椡抂巕偺揹埑偺娭學偼丄
|
亄擖椡丂亅擖椡
|
|
嘍
|
廳梫側惈幙嘇嘊傛傝丄僆儁傾儞僾偺弌椡抂巕偺忬懺偼丄
|
|
|
嘐
|
弌椡抂巕偺揹埑偼丄
|
倁
|
俋.俀. 摎
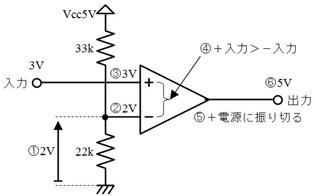
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
暘埑偺朄懃偱丄俀俀倠偺椉抂揹埑偼丄
乮廳梫側惈幙嘋偱丄亅擖椡抂巕偵揹棳偑棳傟側偄偺偱丄暘埑偺朄懃偑巊偊傑偡乯
|
俀倁
|
|
嘇
|
亅擖椡抂巕偺揹埑偼丄
|
俀倁
|
|
嘊
|
亄擖椡抂巕偺揹埑偼丄
|
俁倁
|
|
嘋
|
亄擖椡偲亅擖椡抂巕偺揹埑偺娭學偼丄
|
亄擖椡亜亅擖椡
|
|
嘍
|
廳梫側惈幙嘇嘊傛傝丄僆儁傾儞僾偺弌椡抂巕偺忬懺偼丄
|
亄偵怳傝愗傞
|
|
嘐
|
弌椡抂巕偺揹埑偼丄
|
俆倁
|
偮傑傝丄偙偺夞楬偵俁倁傪擖椡偟偨応崌丄俆倁偑弌椡偝傟傑偡丅
俋.俁. 楙廗
師偵丄偙偺僐儞僷儗乕僞偵侾倁傪擖椡偟偨偲偒偺夞楬偺忬懺傪峫偊傑偡丅
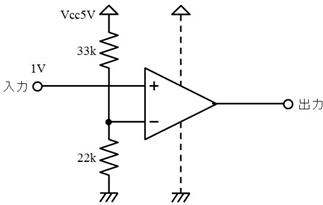
忋恾傪尒偰壓昞偵彂偒崬傒側偑傜峫偊偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
暘埑偺朄懃偱丄俀俀倠偺椉抂揹埑偼丄
|
倁
|
|
嘇
|
亅擖椡抂巕偺揹埑偼丄
|
倁
|
|
嘊
|
亄擖椡抂巕偺揹埑偼丄
|
倁
|
|
嘋
|
亄擖椡偲亅擖椡抂巕偺揹埑偺娭學偼丄
|
亄擖椡丂亅擖椡
|
|
嘍
|
廳梫側惈幙嘇嘊傛傝丄僆儁傾儞僾偺弌椡抂巕偺忬懺偼丄
|
|
|
嘐
|
弌椡抂巕偺揹埑偼丄
乮亅揹尮偼丄偙偺夞楬偱偼僌儔僂儞僪乮侽倁乯偵愙懕偝傟偰偄傑偡乯
|
倁
|
俋.係. 摎
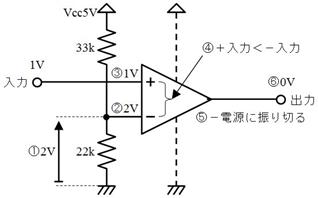
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
暘埑偺朄懃偱丄俀俀倠偺椉抂揹埑偼丄
乮廳梫側惈幙嘋偱丄亅擖椡抂巕偵揹棳偑棳傟側偄偺偱丄暘埑偺朄懃偑巊偊傑偡乯
|
俀倁
|
|
嘇
|
亅擖椡抂巕偺揹埑偼丄
|
俀倁
|
|
嘊
|
亄擖椡抂巕偺揹埑偼丄
|
侾倁
|
|
嘋
|
亄擖椡偲亅擖椡抂巕偺揹埑偺娭學偼丄
|
亄擖椡亙亅擖椡
|
|
嘍
|
廳梫側惈幙嘇嘊傛傝丄僆儁傾儞僾偺弌椡抂巕偺忬懺偼丄
|
乕偵怳傝愗傞
|
|
嘐
|
弌椡抂巕偺揹埑偼丄
乮亅揹尮偼丄偙偺夞楬偱偼僌儔僂儞僪乮侽倁乯偵愙懕偝傟偰偄傑偡乯
|
侽倁
|
偮傑傝丄偙偺夞楬偵侾倁傪擖椡偟偨応崌丄俆倁偑弌椡偝傟傑偡丅
俋.俆. 楙廗
壓恾偺夞楬偺擖椡揹埑傪丄侽乣俆倁偺斖埻偱曄壔偝偣偨偲偒偺丄弌椡偺揹埑偺條巕傪壓恾塃懁偺僌儔僼偵婰擖偟偰壓偝偄丅
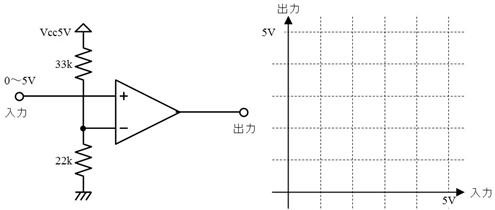
俋.俇. 摎
擖椡揹埑俀倁傪嫬栚偵丄偦傟傛傝擖椡偑崅偄偲偒偼丄弌椡偼俆倁丄偦傟傛傝擖椡偑掅偄偲偒偼丄弌椡偼侽倁偲側傝傑偡丅偙偺傛偆側嫬栚偺揹埑傪乽僗儗僢僔儑儖僪(threshold)揹埑乿偲屇傃傑偡丅
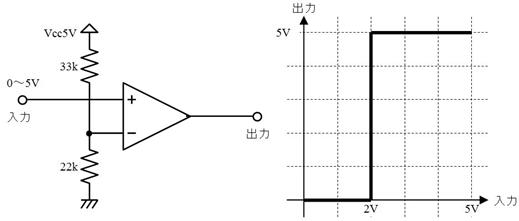
亄擖椡抂巕偵擖椡傪壛偊傞僐儞僷儗乕僞偱偼丄亅擖椡抂巕偺揹埑傪婎弨偵丄擖椡偑崅偗傟偽亄偵怳傝愗傝丄擖椡偑掅偗傟偽丄亅偵怳傝愗傝傑偡丅
俋.俈. 楙廗
壓恾偺僐儞僷儗乕僞偼偙傟傑偱専摙偟偰偒偨夞楬偺亄擖椡偲亅擖椡傪擖傟懼偊偰偄傑偡丅
壓恾偺夞楬偺擖椡揹埑傪丄侽乣俆倁偺斖埻偱曄壔偝偣偨偲偒偺丄弌椡偺揹埑偺條巕傪壓恾塃懁偺僌儔僼偵婰擖偟偰壓偝偄丅
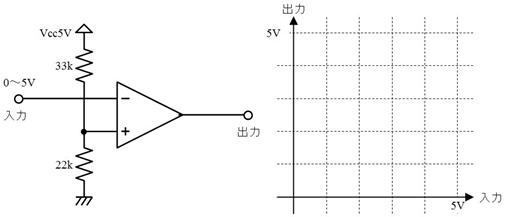
俋.俉. 摎
擖椡揹埑俀倁傪嫬栚偵丄偦傟傛傝擖椡偑崅偄偲偒偼丄弌椡偼侽倁丄偦傟傛傝擖椡偑掅偄偲偒偼丄弌椡偼俆倁偲側傝傑偡丅
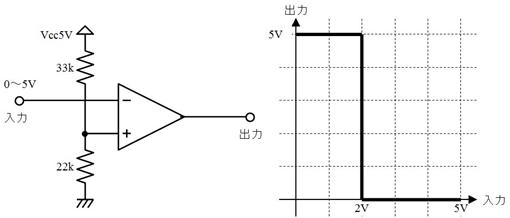
亅擖椡抂巕偵擖椡傪壛偊傞僐儞僷儗乕僞偱偼丄亄擖椡抂巕偺揹埑傪婎弨偵丄擖椡偑崅偗傟偽亅偵怳傝愗傝丄擖椡偑掅偗傟偽丄亄偵怳傝愗傝傑偡丅偮傑傝丄亄擖椡抂巕偵擖椡傪壛偊傞僞僀僾偲偼丄弌椡偺忬懺偑媡偵側傝傑偡丅
擖椡偵巊偆抂巕傪慖傇偙偲偱僐儞僷儗乕僞偺摦嶌傪壓昞偺傛偆偵曄偊傞偙偲偑偱偒傑偡丅
|
僐儞僷儗乕僞偺擖椡抂巕偲摦嶌
|
|
擖椡偵巊偆抂巕
|
擖椡偑崅偄偲偒
|
擖椡偑掅偄偲偒
|
僐儞僷儗乕僞偺僞僀僾
|
|
亄抂巕
|
亄偵怳傝愗傞
|
亅偵怳傝愗傞
|
旕斀揮僐儞僷儗乕僞
|
|
亅抂巕
|
亅偵怳傝愗傞
|
亄偵怳傝愗傞
|
斀揮僐儞僷儗乕僞
|
侾. 斀揮憹暆夞楬
擖椡揹埑偑忋偑傞偲丄媡偵弌椡揹埑偑壓偑傞偨傔丄斀揮憹暆婍偲屇偽傟偰偄傑偡丅亄擖椡偑愙抧偝傟偰偄傞帠偑摿挜偱偡丅偙偺僞僀僾偺夞楬偼丄慺巕偺摿惈傪慺捈偵堷偒弌偡偺偱丄僼傿儖僞傗旕慄宍夞楬摍丄條乆側墳梡夞楬偵棙梡偝傟傑偡丅
偝偰丄壓恾偵斀揮憹暆夞楬傪帵偟傑偡丅弌椡抂巕偺揹埑偑丄俀倠兌傪捠偠偰亅擖椡偵夞傝崬傫偱偄傑偡偐傜丄晧婣娨偺夞楬偱偡丅
侾.侾. 楙廗
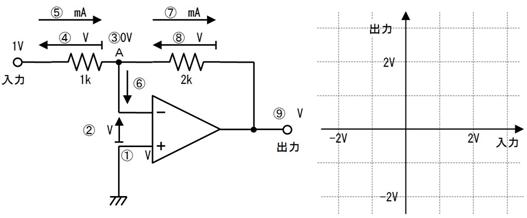
忋恾傪尒偰壓昞偵彂偒崬傒側偑傜峫偊丄忋恾塃懁偺僌儔僼偵擖弌椡摿惈傪彂偒崬傫偱偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
傾乕僗偵愙懕偝傟偰偄傞偺偱丄亄擖椡抂巕偺揹埑偼丄
|
|
|
嘇
|
晧婣娨偺夞楬偩偐傜丄亄擖椡偲亅擖椡偺嵎偼丄
|
|
|
嘊
|
偙偺偨傔丄俙揰偺揹埑偼丄
|
|
|
嘋
|
擖椡揹埑侾倁偲俙揰偺揹埑偺嵎偐傜丄侾倠兌偺椉抂揹埑偼丄
|
|
|
嘍
|
僆乕儉懃傛傝丄侾倠兌偵棳傟傞揹棳偼丄
|
|
|
嘐
|
廳梫側惈幙偐傜丄亅擖椡抂巕偵棳傟傞揹棳偼丄
|
|
|
嘑
|
俙揰偵僉儖僸懃傪偮偐偭偰丄俀倠兌偵棳傟傞揹棳偼丄
|
|
|
嘒
|
僆乕儉懃偐傜丄俀倠兌偺椉抂揹埑偼丄
|
|
|
嘓
|
弌椡偼丄俙揰傛傝嘒偺揹埑偩偗壓偑偭偨揹埑偩偐傜丄
|
|
侾.俀. 摎
擖椡偵宷偑偭偨侾倠兌傪乽擖椡掞峈乿丄弌椡偵宷偑偭偨俀倠兌傪乽婣娨掞峈乿偲屇傃傑偡丅
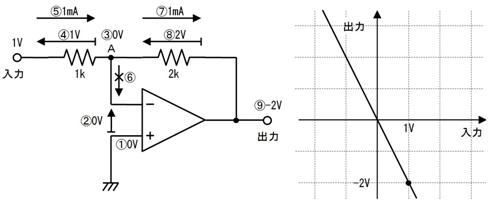
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
傾乕僗偵愙懕偝傟偰偄傞偺偱丄亄擖椡抂巕偺揹埑偼丄
|
侽倁
|
|
嘇
|
晧婣娨偺夞楬偩偐傜丄亄擖椡偲亅擖椡偺嵎偼丄
|
侽倁
|
|
嘊
|
偙偺偨傔丄俙揰偺揹埑偼丄
|
侽倁
|
|
嘋
|
擖椡揹埑侾倁偲俙揰偺揹埑偺嵎偐傜丄侾倠兌偺椉抂揹埑偼丄
|
侾倁
|
|
嘍
|
僆乕儉懃傛傝丄侾倠兌偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘐
|
廳梫側惈幙偐傜丄亅擖椡抂巕偵棳傟傞揹棳偼丄
|
侽俙
|
|
嘑
|
俙揰偵僉儖僸懃傪偮偐偭偰丄俀倠兌偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘒
|
僆乕儉懃偐傜丄俀倠兌偺椉抂揹埑偼丄
|
俀倁
|
|
嘓
|
弌椡偼丄俙揰傛傝嘒偺揹埑偩偗壓偑偭偨揹埑偩偐傜丄
|
亅俀倁
|
僆儁傾儞僾傪巊偭偨憹暆婍偼僔乕僜乕偵偨偲偊傞偙偲傕偱偒傑偡丅壓恾偵斀揮憹暆婍偺條巕傪帵偟傑偡丅
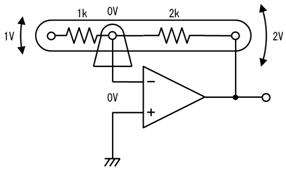
亅擖椡偼亄擖椡偲摨偠揹埑偵側傞偨傔丄忢偵侽倁偱偡丅偙偺偨傔丄僔乕僜乕偺拞墰偺巟揰偩偲峫偊傑偡丅擖椡懁偑侾倠兌側偺偱榬偺挿偝偑侾倣丄弌椡懁偑俀倠兌側偺偱榬偺挿偝偑俀倣偲峫偊傑偡丅巟揰偑屌掕偝傟偰偄傞偨傔丄擖椡懁偑侾倁忋偑傞偲丄弌椡懁偑俀倁壓偑傝丄媡偵擖椡懁偑侾倁壓偑傞偲丄弌椡懁偑俀倁忋偑傝傑偡丅
壓恾偼旕斀揮憹暆夞楬偺條巕偱偡丅
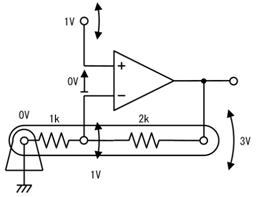
侾倠兌偺嵍懁偼傾乕僗乮侽倁乯偵愙懕偝傟偰偄傞偨傔丄僔乕僜乕偺嵍抂傪巟揰偩偲峫偊傑偡丅亄擖椡抂巕傪侾倁忋壓偝偣傞偲丄乮亄擖椡亖亅擖椡偼摨偠揹埑側偺偱乯亅擖椡抂巕傕侾倁忋壓偟丄僔乕僜乕偺摥偒偱丄弌椡抂巕偼俁倁忋壓偟傑偡丅
儐僯僥傿僎僀儞憹暆婍傗丄旕斀揮憹暆婍偼丄乮僆儁傾儞僾偺亄擖椡抂巕傪丄偦偺傑傑擖椡偵巊梡偟偰偄偨偨傔乯擖椡偵乮杦偳乯揹棳偑棳傟傑偣傫偱偟偨丅偟偐偟丄壓恾偵帵偡傛偆偵丄斀揮憹暆夞楬偼擖椡懁偺侾倠兌偵揹棳偑棳傟偰摦嶌偟傑偡丅偱偡偐傜丄揹埑寁偺擖椡晹摍偵偼揔偟傑偣傫丅
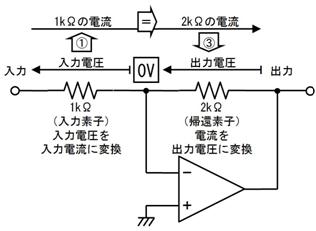
偟偐偟丄忋恾偺乮亄擖椡偑愙抧偝傟偨乯僞僀僾偺夞楬偼丄埲壓偵愢柧偡傞棟桼偵傛傝丄僼傿儖僞傗曄姺夞楬摍偺乮怣崋偺惈幙傪曄壔偝偣傞傛偆側乯僆儁傾儞僾傜偟偄條乆側梡搑偵妶梡偝傟傑偡丅
側偤側傜偙偺夞楬偱偼丄忋恾偵帵偡傛偆偵丄傑偢丄侾倠兌偺塃懁乮亅擖椡抂巕乯偑侽倁偱偡偐傜丄擖椡揹埑偑惓妋偵侾倠兌偵壛傢傝傑偡丅偦偺寢壥嘆侾倠兌偵偼擖椡揹埑偵惓妋偵懳墳偟偨揹棳偑棳傟傑偡丅師偵丄嘇侾倠兌偵棳傟偨揹棳偼丄乮擖椡抂巕偵偼揹棳偑棳傟側偄偺偱乯慡偰俀倠兌偵棳傟傑偡丅嵟屻偵丄俀倠兌偺嵍懁偑侽倁偱偡偐傜丄嘊俀倠兌偵棳傟偨揹棳偱敪惗偡傞揹埑偑丄偦偺傑傑弌椡揹埑偲側傝傑偡丅
偮傑傝丄忋恾偵帵偡傛偆偵丄侾倠兌偑乽擖椡揹埑傪揹棳偵曄姺偡傞慺巕乿丄俀倠兌偑乽揹棳傪弌椡揹埑偵曄姺偡傞慺巕乿偲偟偰嶌梡偟傑偡丅偙偺摿挜偵傛傝丄侾倠兌乮擖椡慺巕乯傗俀倠兌乮婣娨慺巕乯偺戙傢傝偵條乆側慺巕傗夞楬傪巊梡偡傞偙偲偱丄慺巕傗夞楬偺帩偮揹埑偲揹棳偺娭學傪丄偦偺傑傑夞楬偺摿惈偲偟偰棙梡偡傞帠偑偱偒傞偺偱偡丅
偙偙偱偼丄岎棳棟榑偺峫偊曽傪巊偭偰僆儁傾儞僾傪巊偭偨斀揮憹暆夞楬傪専摙偟偰偄傑偡丅夞楬偺摦嶌傪徻偟偔専摙偟偨偄応崌偵偼曋棙側峫偊曽偱偡偑丄抦傜側偔偰傕戝偒側栤戣偼偁傝傑偣傫偐傜丄嫽枴偑側偗傟偽撉傒旘偽偡偙偲傕偱偒傑偡丅撪梕揑偵偼丄捈棳偱偺揹埑乛揹棳偑丄暋慺揹埑乛暋慺揹棳偵丄憹暆棪偑揱払娭悢偵柤慜傪曄偊偨偩偗偱偡丅
偝偰丄斀揮憹暆婍傪岎棳棟榑偱峫偊傞偲丄掞峈俼傪僀儞僺乕僟儞僗倅偵彂偒姺偊偰丄壓恾偺傛偆偵側傝傑偡丅
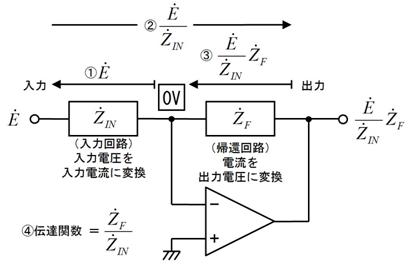
擖椡偵嘆岎棳揹埑俤偑壛傢傞偲丄嘇俤乛倅俬俶偺揹棳偑棳傟丄偦偺揹棳偑偦偺傑傑婣娨夞楬偵傕棳傟傞偨傔丄弌椡揹埑偼丄嘊俤亊倅俥乛倅俬俶偲側傝傑偡丅弌椡乛擖椡偑揱払娭悢偱偡偐傜丄嘋揱払娭悢偼丄倅俥乛倅俬俶偲嬌傔偰僔儞僾儖偵側傝傑偡丅乮嬌惈偼柍帇偟偰偄傑偡乯
偙偺傛偆偵丄擖椡夞楬偲婣娨夞楬偺僀儞僺乕僟儞僗偺斾偑丄偦偺傑傑夞楬偺揱払娭悢偵側傞偨傔丄巚偄捠傝偺摿惈偺夞楬傪嶌傞偙偲偑偱偒傞偺偱偡丅偨偲偊偽丄屻偵愢柧偡傞壓恾偺夞楬偼丄
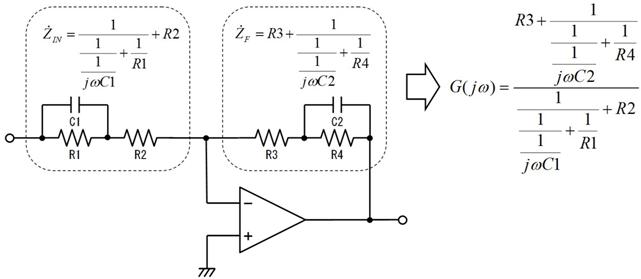
偙偺傛偆偵丄暲楍僀儞僺乕僟儞僗偲捈楍僀儞僺乕僟儞僗偺寁嶼偩偗抦偭偰偄傟偽丄揱払娫憙傪媮傔傞偙偲偑偱偒傑偡丅偦偟偰丄揱払娭悢偝偊暘傟偽丄昁梫側摿惈傪俤倶們倕倢偱昞帵偝偣傞偙偲偑偱偒傑偡丅
恾拞偺幃傪尒偰傕乽暘悢偑戲嶳弌偰偒偰丄倞傕擖偭偰傞偟丄擄偟偦偆偩乿偲偄偆怱攝偼慡偔偁傝傑偣傫丅弌偰偒偨悢幃傪懱嵸傛偔曄宍偡傞偲偄偆乮妛峑偱愱傜楙廗偡傞嶌嬈偺乯昁梫偼柍偔偰丄偦偺傑傑俤倶們倕倢偵擖椡偟偰抣傪媮傔傟偽椙偄偺偱偡丅
忋偺揱払娭悢偺抣偼丄壓恾偺娙扨側俤倶們倕倢僔乕僩偱媮傔傞帠偑偱偒傑偡丅壓恾偺僔乕僩偱偼丄夋柺嵍忋俛俀僙儖偵丄冎偺抣偑偁傝丄偙偺抣傪屻偱曄壔偝偣偰廃攇悢摿惈傪寁嶼偟傑偡丅偦偺俀偮壓偺俛係僙儖偵偼偙偺僔乕僩偺寁嶼寢壥偱偁傞丄冎偵懳墳偟偨揱払娭悢偺抣偑昞帵偝傟傑偡丅

俛俇乣俛侾侾偼掞峈抣傗僐儞僨儞僒梕検偱偡丅俠俇乣俢侾侾僙儖偱偼丄巊傢傟傞慺巕偺僀儞僺乕僟儞僗傗傾僪儈僞儞僗傪昞帵偝偣偰偄傑偡丅偄偢傟偐娙扨側曽乮掞峈側傜僀儞僺乕僟儞僗丄僐儞僨儞僒側傜傾僪儈僞儞僗乯傪寁嶼偟丄懠曽偼媡悢傪寁嶼偟偰昞帵偝偣偰偄傑偡丅
偙傟傜慺巕偺抣傪尦偵丄俠侾俁僙儖乣俢侾係僙儖偱偼擖椡夞楬偺僀儞僺乕僟儞僗丄俠侾俇僙儖乣俢侾俈僙儖偼婣娨夞楬偺僀儞僺乕僟儞僗傪寁嶼偟偰偄傑偡丅婛偵慺巕偺僀儞僺乕僟儞僗偲傾僪儈僞儞僗偺椉曽偑昞帵偝傟偰偄傞偺偱丄捈楍晹暘偼僀儞僺乕僟儞僗傪懌偟嶼丄暲楍晹暘偼傾僪儈僞儞僗傪懌偟嶼偡傞偩偗偱偡丅偼偭偒傝尵偭偰丄堦搙幃傪棫偰偰慺巕偺抣傪戙擖偡傞傛傝丄夞楬恾偐傜忋偺傛偆側俤倶們倕倢僔乕僩傪嶌傞曽偑梋掱妝偱偡丅
偙偺傛偆偵偟偰媮傔偨丄婣娨夞楬偺僀儞僺乕僟儞僗傪丄擖椡夞楬偺僀儞僺乕僟儞僗偱妱傟偽丄俛係僙儖偺揱払娭悢偺抣傪媮傔傞偙偲偑偱偒傑偡丅
屻偼丄廃攇悢冎偺抣傪條乆偵曄壔偝偣偰僌儔僼傪昤偔偩偗偱偡偑丄庤擖椡偱偼庤娫偑妡偐傝傑偡偐傜丄儅僋儘傪巊偄傑偡丅偙偙偱偼丄昗弨儌僕儏乕儖偵師偺傛偆側儅僋儘傪嶌偭偰偄傑偡丅偙偺儅僋儘偼丄冎乮俛俀僙儖乯偺抣傪師乆偲曄壔偝偣偰丄偦偺帪偺俧乮倞冎乯乮俛係僙儖乯偺抣傪庢傝弌偟丄俥楍偲俧楍偵暲傋偰曐懚偟傑偡丅
|
Option
Explicit
Public
Sub 寁嶼()
Dim i As Long
Dim omega As Double
For i = 0 To 100
omega = 10 ^ ((i - 50) / 5)
Worksheets("Sheet1").Range("B2").Value = omega
Worksheets("Sheet1").Cells(i + 2, 6) = omega
Worksheets("Sheet1").Cells(i + 2, 7) =
Worksheets("Sheet1").Range("B4").Value
Next
End
Sub
|
儊僯儏乕僶乕偐傜乽寁嶼乿儅僋儘傪幚峴偡傞偙偲傕偱偒傑偡偟丄僣乕儖僶乕偵儃僞儞傪愝偗偰丄僋儕僢僋堦敪偱幚峴偡傞偙偲傕偱偒傑偡丅
儅僋儘偺幚峴丗乽儊僯儏乕僶乕乿仺乽僣乕儖乿仺乽儅僋儘乿仺乽儅僋儘乿仺乮儅僋儘傪慖戰偟偰乯仺乽幚峴乿
儅僋儘偺僣乕儖僶乕傊偺搊榐丗乽儊僯儏乕僶乕乿仺乽儐乕僓乕愝掕乿仺乽僐儅儞僪乿僞僽偺乽暘椶乿儃僢僋僗偱乽儅僋儘乿慖戰偟丄乽僐儅儞僪乿儃僢僋僗偵昞帵偝傟傞乽儐乕僓乕愝掕偺儊僯儏乕崁栚乿傪忋晹偺僣乕儖僶乕偵僪儔僢僌僪儘僢僾偟偨屻丄僪儘僢僾偟偰偱偒偨乽儐乕僓乕愝掕偺儊僯儏乕崁栚乿傪塃僋儕僢僋偟偰乽儅僋儘偺搊榐乿傪慖傃丄乽寁嶼乿儅僋儘傪愝掕
儅僋儘傪幚峴偡傞偲丄俥楍偵冎偺抣偑丄俧楍偵冎偵懳墳偟偨揱払娭悢偺抣乮俧乮倞冎乯乯偑昞帵偝傟傑偡偐傜丄埵憡偱傕棙摼偱傕丄岲偒側暔傪寁嶼偝偣偰僌儔僼偵昞帵偱偒傑偡丅壓恾偼冎偐傜廃攇悢傪丄俧乮倞冎乯偐傜棙摼傪寁嶼偟偰昞帵偟偨椺偱偡丅

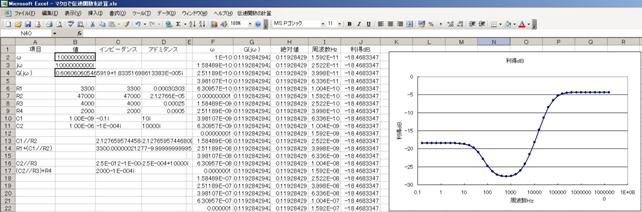
壓恾偺傛偆偵斀揮憹暆婍傪墳梡偟偰丄暋悢偺擖椡揹埑偺崌寁傪弌椡偡傞偙偲偑偱偒傑偡丅
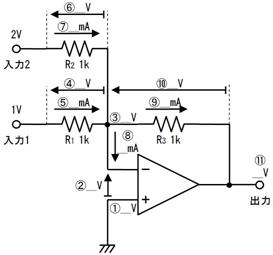
俆.侾. 楙廗
忋恾偺夞楬偺摦嶌傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄乮傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
倁
|
|
嘇
|
亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮侾倠兌偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
倁
|
|
嘊
|
亅擖椡偺揹埑偼丄
|
倁
|
|
嘋
|
俼侾偺椉抂揹埑偼丄
|
倁
|
|
嘍
|
俼侾偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘐
|
俼俀偺椉抂揹埑偼丄
|
倁
|
|
嘑
|
俼俀偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘒
|
亅擖椡偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘓
|
俼俁偵棳傟傞揹棳偼丄
乮嘍丄嘑丄嘒偲僉儖僸懃偐傜丄乯
|
倣俙
|
|
嘔
|
俼俁偺椉抂揹埑偼丄
|
倁
|
|
嘕
|
弌椡揹埑偼丄
|
倁
|
俆.俀. 摎
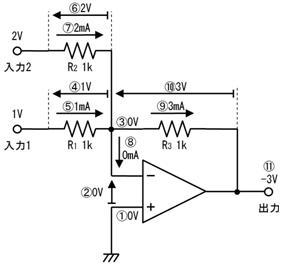
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄乮傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
侽倁
|
|
嘇
|
亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮侾倠兌偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
侽倁
|
|
嘊
|
亅擖椡偺揹埑偼丄
|
侽倁
|
|
嘋
|
俼侾偺椉抂揹埑偼丄
|
侾倁
|
|
嘍
|
俼侾偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘐
|
俼俀偺椉抂揹埑偼丄
|
俀倁
|
|
嘑
|
俼俀偵棳傟傞揹棳偼丄
|
俀倣俙
|
|
嘒
|
亅擖椡偵棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘓
|
俼俁偵棳傟傞揹棳偼丄
乮嘍丄嘑丄嘒偲僉儖僸懃偐傜丄乯
|
俁倣俙
|
|
嘔
|
俼俁偺椉抂揹埑偼丄
|
俁倁
|
|
嘕
|
弌椡揹埑偼丄
|
亅俁倁
|
偙偺傛偆偵丄擖椡侾偲擖椡俀偵壛傢偭偨揹埑偺崌寁偑丄斀揮偟偰弌椡偝傟傑偡丅擖椡偺壓恾偼偝傜偵憹傗偡偙偲傕偱偒傑偡丅傑偨丄擖椡掞峈偺塃懁偼侽倁偺亅擖椡偵愙懕偝傟偰偄傞偨傔丄擖椡侾偺怣崋偑擖椡俀偵媡棳偡傞偙偲傕偁傝傑偣傫丅
壓恾偼乽惓擖椡乿偲乽晧擖椡乿偺嵎傪弌椡偡傞乽嵎摦憹暆夞楬乿偱偡丅偙偺傛偆偵丄俼侾乣俼係偺慡掞峈偵摨偠傪巊梡偡傞偲丄憹暆棪偑侾偵側傝傑偡丅
壓恾偺椺偱偼丄乽晧擖椡乿偵偼俁倁丄乽惓擖椡乿偵偼乮晧擖椡傛傝侾倁崅偄乯係倁偑壛傢偭偰偄傑偡丅乽惓擖椡乿偲乽晧擖椡乿偺嵎偼侾倁偱偡丅
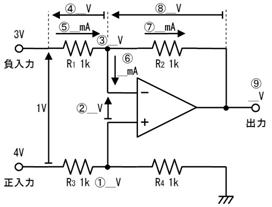
俇.侾. 楙廗
忋恾傪嶲峫偵丄壓昞偵彂偒崬傫偱嵎摦憹暆夞楬偺摦嶌傪専摙偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄
乮惓擖椡偺係倁偑俼俁偲俼係偱暘埑偝傟偰偄傞偐傜丄乯
|
倁
|
|
嘇
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
俼俀偱晧婣娨偑妡偐偭偰偄傞偐傜丄
|
倁
|
|
嘊
|
亅擖椡偺揹埑偼丄
|
倁
|
|
嘋
|
俼侾偺椉抂揹埑偼丄
|
倁
|
|
嘍
|
俼侾偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘐
|
亅擖椡偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘑
|
俼俀偵棳傟傞揹棳偼丄乮嘍丄嘐偲僉儖僸懃偐傜丄乯
|
倣俙
|
|
嘒
|
俼俀偺椉抂揹埑偼丄
|
倁
|
|
嘓
|
弌椡揹埑偼丄乮嘐偲嘒偐傜丄乯
|
倁
|
俇.俀. 摎
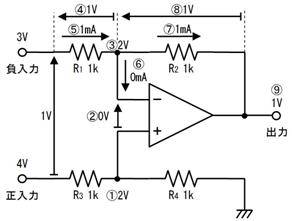
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄
乮惓擖椡偺係倁偑俼俁偲俼係偱暘埑偝傟偰偄傞偐傜丄乯
|
俀倁
|
|
嘇
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
俼俀偱晧婣娨偑妡偐偭偰偄傞偐傜丄
|
侽倁
|
|
嘊
|
亅擖椡偺揹埑偼丄
|
俀倁
|
|
嘋
|
俼侾偺椉抂揹埑偼丄
|
侾倁
|
|
嘍
|
俼侾偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘐
|
亅擖椡偵棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘑
|
俼俀偵棳傟傞揹棳偼丄乮嘍丄嘐偲僉儖僸懃偐傜丄乯
|
侾倣俙
|
|
嘒
|
俼俀偺椉抂揹埑偼丄
|
侾倁
|
|
嘓
|
弌椡揹埑偼丄乮嘐偲嘒偐傜丄乯
|
侾倁
|
嵎摦憹暆夞楬偼丄壓恾乮倎乯偵帵偡偲偍傝晧擖椡傪傾乕僗偵愙懕偡傞偲丄俀攞偺旕斀揮憹暆夞楬偲丄俀暘偺侾偺暘埑夞楬偩偲峫偊傞偙偲偑偱偒傑偡丅偱偡偐傜丄惓擖椡偵俀倁傪擖椡偡傟偽丄偦傟偑暘埑偝傟偰侾倁偲側傝丄俀攞偵憹暆偝傟偰俀倁偑弌椡偝傟傑偡丅
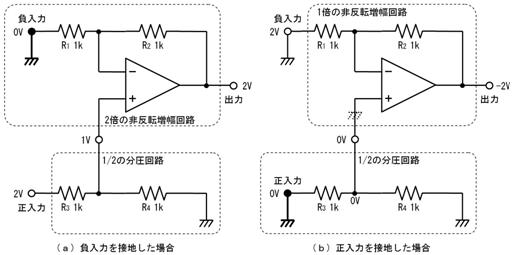
傑偨丄忋恾乮倐乯偵帵偡偲偍傝惓擖椡傪傾乕僗偵愙懕偡傞偲丄侾攞偺斀揮憹暆夞楬偲丄俀暘偺侾偺暘埑夞楬偩偲峫偊傞偙偲偑偱偒傑偡丅偱偡偐傜丄晧擖椡偵俀倁傪擖椡偡傟偽丄偦傟偑斀揮偝傟偰亅俀倁偑弌椡偝傟傑偡丅
偙偺傛偆偵丄惓擖椡偵壛偊偨揹埑偼斀揮偝傟偢偵弌椡偝傟丄晧擖椡偵壛偊偨揹埑偼斀揮偟偰弌椡偝傟傑偡丅偦偺寢壥丄惓擖椡偲晧擖椡偺嵎偑弌椡偝傟傑偡丅
嵎摦憹暆夞楬偱揹埑嵎傪憹暆偟偰弌椡偡傞応崌偼丄壓恾偺傛偆偵 俼俀 亖 憹暆棪 亊
俼侾 偲偟傑偡丅乮俼侾亖俼俁丄俼俀亖俼係偲偟傑偡乯偱偡偐傜丄壓恾偺夞楬偺憹暆棪偼侾侽攞偱偡丅
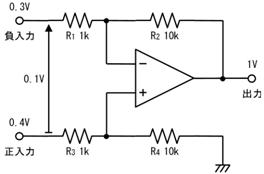
嵎摦憹暆夞楬偼擖椡抂巕偵揹棳偑棳傟偰摦嶌偡傞偨傔丄應掕偡傞夞楬偵塭嬁傪梌偊傑偡丅偙傟傪杊巭偡傞偵偼丄師偵愢柧偡傞寁應憹暆夞楬傪巊偄傑偡丅
寁憰憹暆夞楬乮僀儞僗僣儖儊儞僥乕僔儑儞丒傾儞僾乛寁應憰抲憹暆夞楬乯偼丄壓恾偵帵偡傛偆偵丄嵎摦憹暆夞楬偺慜抜偵斀揮憹暆夞楬傪捛壛偟丄擖椡偵棳傟傞揹棳傪彫偝偔乮擖椡僀儞僺乕僟儞僗傪崅偔乯偟偨傕偺偱偡丅俼俆亖俼俇偲偟丄俼俈偱憹暆棪傪愝掕偱偒傑偡丅
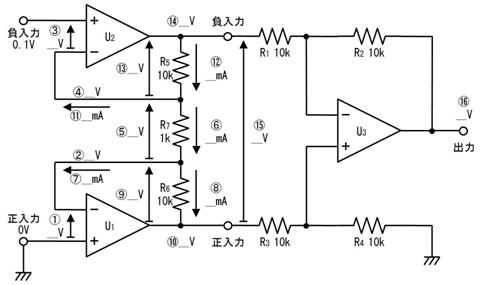
俈.侾. 楙廗
忋恾偺寁憰憹暆夞楬偺惓擖椡傪傾乕僗偵愙懕偟丄晧擖椡偵侽丏侾倁傪壛偊偨応崌偺奺晹偺揹埑乛揹棳傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
倀侾偺亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮俼俇偱晧婣娨偑妡偐偭偰偄傞偺偱丄乯
|
倁
|
|
嘇
|
倀侾偺亅擖椡偺揹埑偼丄
|
倁
|
|
嘊
|
倀俀偺亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮俼俆偱晧婣娨偱妡偐偭偰偄傞偺偱丄乯
|
倁
|
|
嘋
|
倀俀偺亅擖椡偺揹埑偼丄
|
倁
|
|
嘍
|
俼俈偺椉抂揹埑偼丄
乮嘇偲嘋偐傜丄乯
|
倁
|
|
嘐
|
俼俈偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘑
|
倀侾偺亅擖椡偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘒
|
俼俇偵棳傟傞揹棳偼丄
乮嘐丄嘑偲僉儖僸懃偐傜丄乯
|
倣俙
|
|
嘓
|
俼俇偺椉抂揹埑偼丄
|
倁
|
|
嘔
|
倀侾偺弌椡抂巕偺揹埑偼丄
|
倁
|
|
嘕
|
倀俀偺亅擖椡偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘖
|
俼俆偵棳傟傞揹棳偼丄
乮嘋丄嘐偲僉儖僸懃偐傜丄乯
|
倣俙
|
|
嘗
|
俼俆偺椉抂揹埑偼丄
|
倁
|
|
嘙
|
倀俀偺弌椡抂巕偺揹埑偼丄
|
倁
|
|
嘚
|
倀侾偺弌椡抂巕偐傜丄倀俀偺弌椡抂巕傑偱偺揹埑偼丄
|
倁
|
|
嘜
|
倀俁偺弌椡揹埑偼丄
乮侾攞偺嵎摦憹暆夞楬偩偐傜丄乯
|
倁
|
俈.俀. 摎
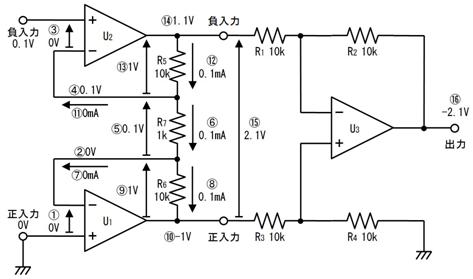
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
倀侾偺亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮俼俇偱晧婣娨偑妡偐偭偰偄傞偺偱丄乯
|
侽倁
|
|
嘇
|
倀侾偺亅擖椡偺揹埑偼丄
|
侽倁
|
|
嘊
|
倀俀偺亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮俼俆偱晧婣娨偱妡偐偭偰偄傞偺偱丄乯
|
侽倁
|
|
嘋
|
倀俀偺亅擖椡偺揹埑偼丄
|
侽丏侾倁
|
|
嘍
|
俼俈偺椉抂揹埑偼丄
乮嘇偲嘋偐傜丄乯
|
侽丏侾倁
|
|
嘐
|
俼俈偵棳傟傞揹棳偼丄
|
侽丏侾倣俙
|
|
嘑
|
倀侾偺亅擖椡偵棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘒
|
俼俇偵棳傟傞揹棳偼丄
乮嘐丄嘑偲僉儖僸懃偐傜丄乯
|
侽丏侾倣俙
|
|
嘓
|
俼俇偺椉抂揹埑偼丄
|
侾倁
|
|
嘔
|
倀侾偺弌椡抂巕偺揹埑偼丄
|
亅侾倁
|
|
嘕
|
倀俀偺亅擖椡偵棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘖
|
俼俆偵棳傟傞揹棳偼丄
乮嘋丄嘐偲僉儖僸懃偐傜丄乯
|
侽丏侾倣俙
|
|
嘗
|
俼俆偺椉抂揹埑偼丄
|
侾倁
|
|
嘙
|
倀俀偺弌椡抂巕偺揹埑偼丄
|
侾丏侾倁
|
|
嘚
|
倀侾偺弌椡抂巕偐傜丄倀俀偺弌椡抂巕傑偱偺揹埑偼丄
|
俀丏侾倁
|
|
嘜
|
倀俁偺弌椡揹埑偼丄
乮侾攞偺嵎摦憹暆夞楬偩偐傜丄乯
|
亅俀丏侾倁
|
偙偺傛偆偵丄慜抜偺旕斀揮憹暆夞楬偺嵎摦怣崋憹暆棪偼乮俼俆亄俼俇乯乛俼俈偲側傝傑偡丅
俉. 僆儁傾儞僾偲墳梡夞楬偺廃攇悢摿惈
壓恾塃懁偵懢偄奃怓慄偱帵偡傛偆偵丄僆儁傾儞僾杮懱偺廃攇悢乮棙摼乯摿惈偼丄塃尐壓偑傝偱偡丅偙傟偼丄僴儞僪儖傪夞偟偰揹埑傪忋偘壓偘偡傞偺偵帪娫偑妡偐傞偨傔偱偡丅乮僴儞僪儖傪夞偡懍偝偼堦掕偱偡偐傜丄忋偘壓偘偺昿搙偑憹偡傎偳丄彮偟偟偐夞偣側偔側傝傑偡乯
壓恾嵍懁偵旕斀揮憹暆婍傪帵偟傑偡丅摨恾偵帵偡偲偍傝丄巊梡偡傞掞峈偵傛偭偰憹暆棪傪暆峀偔愝掕偡傞偙偲偑偱偒傑偡丅壓恾偺椺偱偼丄婣娨掞峈傪俋倠兌丄俋俋倠兌丄俋俋俋倠兌偲曄峏偡傞偙偲偱侾侽攞丄侾侽侽攞丄侾侽侽侽攞偲愝掕偟偰偄傑偡丅
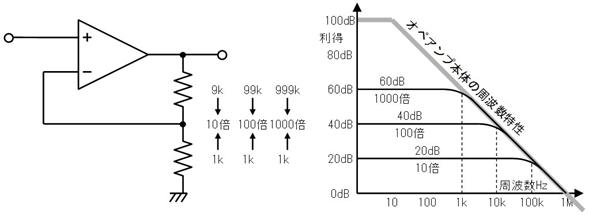
偙偺傛偆偵丄掞峈抣偵傛偭偰偼崅偄憹暆棪傪摼傞偙偲偑偱偒傑偡偑丄忋恾塃懁偺僌儔僼偵奃怓慄偱帵偡乽僆儁傾儞僾杮懱偺廃攇悢摿惈乿傛傝戝偒側憹暆棪偼弌偣傑偣傫丅偙偺偨傔丄憹暆棪傪戝偒偔偡傞傎偳丄幷抐廃攇悢乮偙偙偐傜憹暆棪偑壓偑傞偧丄偲偄偆廃攇悢乯偑掅偔側偭偰峴偒傑偡丅忋偺椺偱偼丄攞棪傪侾侽攞丄侾侽侽攞丄侾侽侽侽攞偲戝偒偔偡傞偲丄幷抐廃攇悢偼侾侽侽倠俫倸丄侾侽倠俫倸丄侾倠俫倸偲掅偔側偭偰偄傑偡丅
偙偺傛偆偵夞楬傪愝寁偡傞忋偱僆儁傾儞僾杮懱偺廃攇悢摿惈偼廳梫偱偡丅偙偺偨傔僨乕僞僔乕僩偱偼壓昞偺傛偆側條乆側曽朄偱廃攇悢摿惈偑帵偝傟傑偡丅
|
柤徧傗扨埵
|
愢柧
|
忋恾偺椺
|
|
廃攇悢摿惈恾
|
僌儔僼偱恾帵偝傟傞
|
忋恾塃懁奃怓偺僌儔僼
|
|
儐僯僥傿僎僀儞廃攇悢
乵俫倸乶
|
乮晧婣娨傪妡偗側偄偲偒偵乯憹暆棪偑侾攞乮棙摼偑侽倓俛乯偵側傞廃攇悢乮壓恾嘆乯
|
侾俵俫倸
|
|
俧俛愊
僎僀儞僶儞僪僂傿僘
乵俫倸乶
|
乮晧婣娨傪妡偗側偄偲偒偺乯嵟崅偺憹暆棪偲憹暆棪偑壓偑傝巒傔傞廃攇悢偺愊乮壓恾嘇乯
|
侾侽俫倸亊侾侽枩攞(100dB)
亖侾俵俫倸
|
|
偁傞廃攇悢乮擟堄乯偱偺廃攇悢偲憹暆棪偺愊乮壓恾嘊乯
|
侾侽倠俫倸亊侾侽侽攞
亖侾俵俫倸
|
仸嵟崅偺憹暆棪偼丄晧婣娨傪妡偗側偄偲偒偺捈棳偺憹暆棪偱乽僆乕僾儞儖乕僾乮晧婣娨側偟偺乯僎僀儞乿偲傕屇偽傟傑偡丅
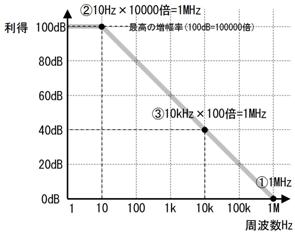
幷抐廃攇悢偑崅偔丄偦偺偆偊憹暆棪傕戝偒偄憹暆婍傪愝寁偡傞偵偼丄壓恾忋懁偺傛偆偵丄廃攇悢摿惈偺桪傟僆儁傾儞僾傪巊偆偐丄壓恾壓懁偺傛偆偵丄憹暆棪傪梷偊乮偰幷抐廃攇悢傪崅傔乯偨憹暆夞楬傪暋悢愙懕偟傑偡丅壓恾偼忋壓嫟偵丄揹埑憹暆棪侾侽侽侽攞丄幷抐廃攇悢侾侽侽倠俫倸偺憹暆婍偺椺偱偡丅
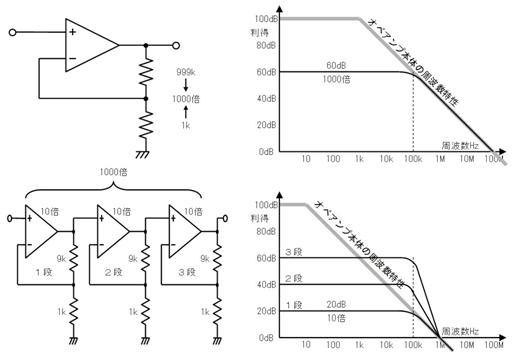
俉.侾. 楙廗
僆乕僾儞儖乕僾僎僀儞俉侽倓俛丄俧俛愊俁侽侽倠俫倸偺僆儁傾儞僾偺廃攇悢摿惈傪壓恾偵揰慄偱嶌恾偟丄偙偺僆儁傾儞僾傪巊偭偰嶌偭偨侾侽侽攞偺憹暆婍偺廃攇悢摿惈傪幚慄偱彂偒壛偊丄憹暆婍偺幷抐廃攇悢乮僇僢僩僆僼廃攇悢乯傪摎偊偰偔偩偝偄丅
僇僢僩僆僼廃攇悢乮倖俠乯丂丂丂丂倠俫倸
俉.俀. 摎
俉侽倓俛偼揹埑侾侽侽侽侽攞偺帠偱偁傞丅俧俛愊俁侽侽倠俫倸傪嵟戝偺憹暆棪侾侽侽侽侽攞偱妱傞偲丄俁侽俫倸偲側傞偐傜丄偙偺僆儁傾儞僾偼俁侽俫倸埲忋偺廃攇悢偱棙摼偑掅壓偟偰峴偔丅嵟戝偺棙摼偑俉侽倓俛偱偁傞偙偲傪峫偊偰丄壓恾揰慄偺傛偆偵嶌恾偱偒傞丅
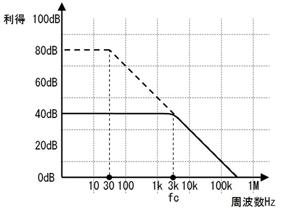
僇僢僩僆僼廃攇悢乮倖俠乯丂丂丂俁倠俫倸
揹埑侾侽侽攞偼係侽倓俛偩偐傜丄憹暆婍偺棙摼偼僆儁傾儞僾杮懱偺棙摼傪墇偊傜傟側偄帠傪峫偊偰丄廃攇悢摿惈偼忋恾幚慄偺傛偆偵側傝丄恾傛傝倖俠偼俁倠俫倸偲暘偐傞丅
昁梫埲忋偵崅偄廃攇悢傑偱憹暆偱偒傞偲丄儔僕僆偺揹攇傪庴怣偟偰岆摦嶌偡傞応崌偑偁傝傑偡偟丄嶨壒傕懡偔側傝傑偡丅傑偨憹暆棪偑掅偄応崌偼丄壓恾偵帵偡傛偆側僆乕僶乕僔儏乕僩偑弌傞応崌傕偁傝傑偡丅
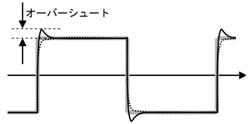
偙偺傛偆側応崌丄壓恾嵍懁偺夞楬恾偵帵偡偲偍傝丄婣娨掞峈偲暲楍偵彫偝側梕検偺婣娨僐儞僨儞僒傪愙懕偡傞偲丄晄梫側崅偄廃攇悢偺憹暆傪梷偊丄僆乕僶乕僔儏乕僩傪柍偔偡偙偲偑偱偒傑偡丅
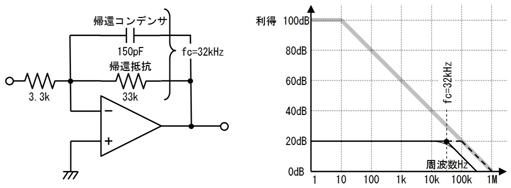
忋恾塃懁偺僌儔僼偺揰慄偑僐儞僨儞僒偺柍偄忬懺丄幚慄偑僐儞僨儞僒傪庢傝晅偗偨応崌偺廃攇悢摿惈偱偡丅俁俁倠兌偲侾俆侽倫俥偱寛傑傞廃攇悢乮倖俠乯傛傝崅偄廃攇悢偱憹暆棪偑壓偑偭偰峴偒傑偡丅
僐儞僨儞僒偺梕検偼丄=1/2/PI()/F1/C1丄忋偺椺偱偼=1/2/PI()/32E3/33E3偱媮傔傞帠偑偱偒傑偡丅乮倖俠偼=1/2/PI()/C1/R1偱偡乯
巊梡偡傞忋尷偺廃攇悢偺俀乣俆攞掱搙偱懷堟傪惂尷偟偰偍偔偺偑丄埨掕摦嶌偺僐僣偱偡丅
俋.侾. 楙廗
壓恾偺斀揮憹暆婍偺憹暆棪傪俆攞偲偟丄懷堟傪侾侽倠俫倸偵惂尷偱偒傞傛偆丄婣娨掞峈偲婣娨僐儞僨儞僒偺抣傪寛掕偟丄憹暆婍偺廃攇悢摿惈傪僌儔僼偵彂偒壛偊偰偔偩偝偄丅
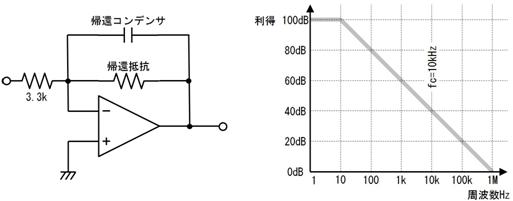
俋.俀. 摎
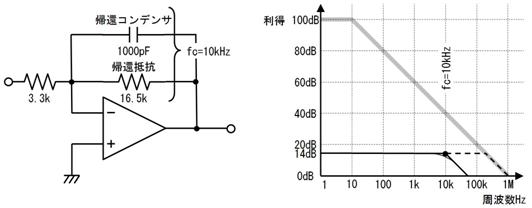
婣娨掞峈偼=5*3.3E3偱侾俇丏俆倠兌丄 婣娨僐儞僨儞僒偼=1/2/pi()/10E3/16.5E3偱丄侾侽侽侽倫俥丅嶲峫傑偱偵丄揹埑憹暆棪俆攞偼=20*LOG(5,10)偱栺侾係倓俛丅
侾侽. 愊暘夞楬
偨偲偊偽壓恾偺傛偆偵丄侾倁傪擖椡偡傞偲侾昩偵侾倁偺惃偄偱丄俀倁傪擖椡偡傞偲侾昩偵俀倁偺惃偄偱丄弌椡偑忋徃偟懕偗傞夞楬傪愊暘夞楬偲屇傃傑偡丅擖椡偑侽倁偺応崌偼丄弌椡揹埑偼曄摦偟傑偣傫丅
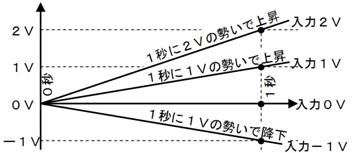
僨僕僞儖寁嶼婡偑柍偄帪戙偵偼丄僔儈儏儗乕僔儑儞傪偡傞偨傔偵廳梫側夞楬偱丄僆儁傾儞僾偼偙偺夞楬傪嶌傞偨傔偵奐敪偝傟偨偲傕尵偊傑偡丅
僆儁傾儞僾傪巊偭偨愊暘夞楬傪壓恾偵帵偟傑偡丅
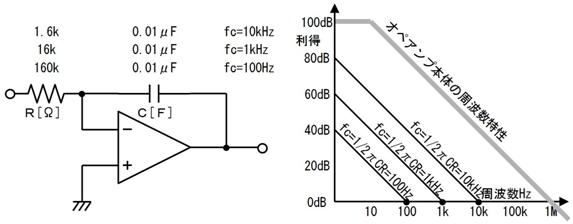
偙偺夞楬偼丄擖椡揹埑偑崅偄掱丄弌椡揹埑偑惃偄椙偔乽壓偑傞乿偺偱丄柤慜偙偦乽愊暘夞楬乿偲屇偽傟偰偄傑偡偑丄摥偒偼乽斀揮愊暘夞楬乿偱偡丅
摦嶌偺僀儊乕僕偼丄擖椡揹埑偵斾椺偟偨揹埑偑俼偵棳傟丄偦偺揹棳偱俠偑廩揹偝傟丄俠偺揹埑偑乮斀揮偟偰乯弌椡揹埑偵側傞丅偦偺偨傔丄堦掕偺揹埑傪壛偊傞偲丄堦掕偺儁乕僗偱俠偑廩揹偝傟丄弌椡揹埑偑崀壓偡傞丄偲偄偆傕偺偱偡丅
崱傑偱愢柧偟偨丄捈棳夞楬傗岎棳夞楬偺峫偊曽傪巊偭偰丄揹埑偺曄壔傗揱払娭悢傪媮傔傞帠偑偱偒傑偡偑丄偦偺徻嵶傪愢柧偡傞偺偼杮彂偺庡栚揑偱偼側偄偺偱屻夞偟偵偟丄愝寁偵昁梫側抣偺媮傔曽傪愭偵徯夘偟傑偡丅
忋恾偺夞楬偺丄掞峈俼傗僐儞僨儞僒梕検俠偼丄擖椡揹埑偲丄弌椡揹埑偺崀壓懍搙偐傜丄師偺傛偆偵寁嶼偱偒傑偡丅
俠
亊 俼
亖 擖椡揹埑乵倁乶
亐 弌椡揹埑偺崀壓懍搙乵倁乛昩乶
傑偨丄偙偺夞楬偼忋恾塃懁偺僌儔僼偺傛偆偵丄廃攇悢偑忋徃偡傞偲憹暆棪偑掅壓偟傑偡丅憹暆棪偑掅壓偟偰侾攞乮侽倓俛乯偵側傞廃攇悢偐傜丄俠傗俼偼師偺傛偆偵寁嶼偱偒傑偡丅
俠
亊 俼
亖 侾
乛乮俀 兾 亊
憹暆棪偑侾攞偲側傞廃攇悢乵俫倸乶乯
=1/2/pi()/F1乵昩乶
傑偨媡偵丄
憹暆棪偑侾攞偲側傞廃攇悢乵俫倸乶亖
侾 乛乮俀 兾 亊俠 亊
俼乯
=1/2/pi()/C1/R1乵俫倸乶
偲丄寁嶼偡傞偙偲偑偱偒傑偡丅俠 亊
俼偼帪掕悢冄乮僞僂乯偲屇傫偱偄傞傕偺偱偡丅
愊暘夞楬偼埨掕摦嶌偡傞応崌偑懡偔丄摿偵埨掕偺偨傔偺岺晇偣偢偵墳梡偡傞偙偲偑偱偒傑偡丅
偨偩偟丄悢昩偐傜悢廫昩傪墇偊傞丄嬌傔偰備偭偔傝偲帪娫傪妡偗偰摦嶌偡傞愊暘夞楬偱偼丄僐儞僨儞僒偺揹壸偑乮彫偝側寠偺奐偄偨僶働僣偺傛偆偵乯楻傟偰偟傑偄丄弌椡揹埑偑晄惓妋偵側傞応崌偑偁傝傑偡丅偙偺傛偆側応崌偼丄楻傟揹棳偺彮側偄僐儞僨儞僒乮億儕僾儘僺儗儞僼傿儖儉僐儞僨儞僒摍乯傪巊偄丄嬻拞偵攝慄偡傞側偳偺岺晇傪偟傑偡丅偙偺傛偆側夞楬偼丄僆儁傾儞僾傗僐儞僨儞僒丄偦傟偵婎斅偑墭傟偰偄傞偩偗偱乮墭傟傪捠偟偰乯揹棳偑楻傟偰偟傑偆偺偱丄僼儔僢僋僗彍嫀塼摍偱鉟楉偵惔憒偟傑偡丅
侾侽.侾. 楙廗
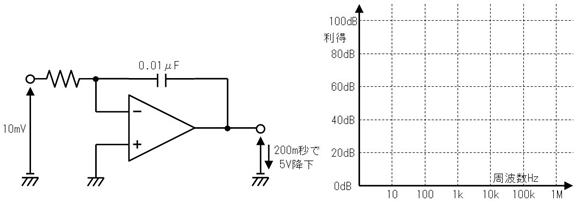
忋恾偵帵偡偲偍傝丄侽丏侽侾兪俥偺僐儞僨儞僒傪巊偭偰丄擖椡侾侽倣倁傪壛偊偨偲偒丄俀侽侽倣昩偺娫偱丄弌椡揹埑偑俆倁崀壓偡傞愊暘夞楬傪丄壓昞偵婰擖偟偰愝寁偟偰偔偩偝偄丅傑偨丄偙偺愊暘夞楬偺廃攇悢摿惈傪忋恾塃懁偺僌儔僼偵婰擖偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
弌椡揹埑偺崀壓懍搙偼丄
|
倁乛昩
|
|
嘇
|
偙偺偲偒偺擖椡揹埑偼丄
|
倣倁
|
|
嘊
|
俠亊俼偺抣乮帪掕悢乯偼丄
|
兪昩
|
|
嘋
|
僐儞僨儞僒偼侽丏侽侾兪俥偩偐傜掞峈偺抣偼
|
倠兌
|
|
嘍
|
憹暆棪偑侾攞偲側傞廃攇悢偼丄
|
俫倸
|
侾侽.俀. 摎
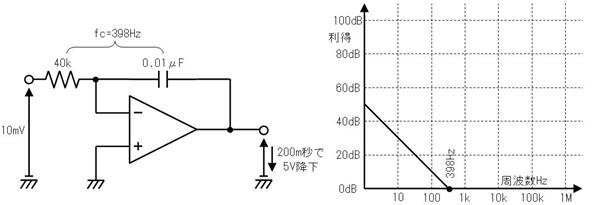
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
弌椡揹埑偺崀壓懍搙偼丄俆倁乛俀侽侽倣昩偱丄
=5/200E-3
|
俀俆倁乛昩
|
|
嘇
|
偙偺偲偒偺擖椡揹埑偼丄
|
侾侽倣倁
|
|
嘊
|
俠亊俼偺抣乮帪掕悢乯偼丄侾侽倣倁亐俀俆倁乛昩偱
=10E-3/25
|
係侽侽兪昩
|
|
嘋
|
僐儞僨儞僒偼侽丏侽侾兪俥偩偐傜掞峈偺抣偼
係侽侽兪昩乛侽丏侽侾兪俥偱=400E-6/0.01E-6
|
係侽倠兌
|
|
嘍
|
憹暆棪偑侾攞偲側傞廃攇悢偼丄俀乛乮俀兾俠俼乯
=1/2/pi()/0.01E-6/40E3
|
俁俋俉俫倸
|
侾侽.俁. 楙廗乮愊暘夞楬偺捈棳専摙乯
婛偵愢柧偟偨曽朄偱愊暘夞楬偼愝寁偱偒傑偡丅
偙偙偱偼丄捈棳夞楬傪暅廗偡傞偨傔偵丄愊暘夞楬偺摦嶌傪捈棳専摙偟傑偡丅婛偵抦偭偰偄傞夞楬傪巊偆偲偒偼丄偙偺傛偆側専摙偼昁梫偁傝傑偣傫丅偟偐偟丄抦傜側偄夞楬偵弌夛偭偨偲偒偼丄捈棳夞楬傪抦幆傪巊偭偰丄摦嶌傪峫偊傞偙偲偑偱偒傑偡丅
偨偩偟丄偙偆偄偭偨愢柧偼丄嫵壢彂揑偱戅孅側忋丄捈偖偵偼栶偵棫偨側偄偺偱丄枅夞偙偺傛偆側専摙傪峴偆偙偲偼峊偊傑偡丅乽抦傜側偄夞楬偑弌偰偒偨傜丄捈棳棟榑偲岎棳棟榑偩乿偲偩偗妎偊偲偄偰壓偝偄丅
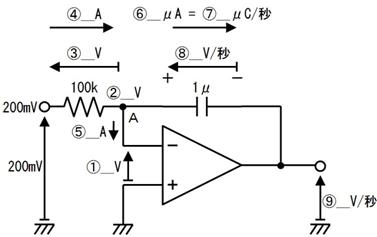
偝偰丄忋恾偺愊暘夞楬偼丄婣娨僐儞僨儞僒傪捠偠偰丄弌椡揹埑偑亅擖椡抂巕偵夞傝崬傫偱偄傑偡偐傜丄晧婣娨偺夞楬偱偡丅忋恾偺夞楬傪丄壓昞偺抣棑偵彂偒崬傫偱捈棳専摙偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偲亅擖椡偺揹埑偼丄晧婣娨偩偐傜丄
|
亄擖椡丂亅擖椡
|
|
嘇
|
俙揰偺揹埑偼丄
|
[倁]
|
|
嘊
|
掞峈偺椉抂揹埑偼丄
|
[倣倁]
|
|
嘋
|
掞峈偵棳傟傞揹棳偼丄僆乕儉懃傛傝丄
|
[兪俙]
|
|
嘍
|
亅擖椡抂巕偵棳傟傞揹棳偼丄
|
[俙]
|
|
嘐
|
僐儞僨儞僒偵棳傟傞揹棳偼丄僉儖僸懃傛傝丄
|
[兪俙]
|
|
嘑
|
僐儞僨儞僒偵侾昩偵棳傟崬傓揹壸偼丄
乮侾俙亖侾俠乛昩偩偐傜丄乯
|
[兪俠乛昩]
|
|
嘒
|
僐儞僨儞僒偺揹埑偺侾昩偁偨傝偺忋徃偼丄
乮僐儞僨儞僒偺揹埑亖揹壸[俠]乛梕検[俥]偩偐傜丄僐僢僾偵棳傟崬傓悈傪憐憸偟偰丄乯
|
[倁乛昩]
|
|
嘓
|
弌椡揹埑偺侾昩偁偨傝偺曄壔偼丄
乮僐儞僨儞僒偺揹埑栴報偺岦偒偵拲堄偟偰丄乯
|
[倁乛昩]
|
侾侽.係. 摎
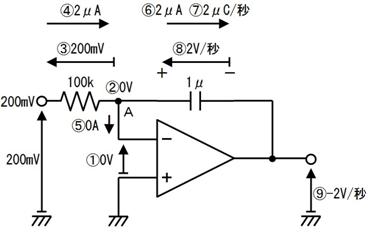
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偲亅擖椡偺揹埑偼丄晧婣娨偩偐傜丄
|
亄擖椡亖亅擖椡
|
|
嘇
|
俙揰偺揹埑偼丄
|
侽[倁]
|
|
嘊
|
掞峈偺椉抂揹埑偼丄
|
俀侽侽[倣倁]
|
|
嘋
|
掞峈偵棳傟傞揹棳偼丄僆乕儉懃傛傝丄=200E-3/100E3
|
俀[兪俙]
|
|
嘍
|
亅擖椡抂巕偵棳傟傞揹棳偼丄
|
侽[俙]
|
|
嘐
|
僐儞僨儞僒偵棳傟傞揹棳偼丄僉儖僸懃傛傝丄
|
俀[兪俙]
|
|
嘑
|
僐儞僨儞僒偵侾昩偵棳傟崬傓揹壸偼丄
乮侾俙亖侾俠乛昩偩偐傜丄乯
|
俀[兪俠乛昩]
|
|
嘒
|
僐儞僨儞僒偺揹埑偺侾昩偁偨傝偺忋徃偼丄
乮僐儞僨儞僒偺揹埑亖揹壸[俠]乛梕検[俥]偩偐傜丄僐僢僾偵棳傟崬傓悈傪憐憸偟偰丄乯=2E-6/1E-6
|
俀[倁乛昩]
|
|
嘓
|
弌椡揹埑偺侾昩偁偨傝偺曄壔偼丄
乮僐儞僨儞僒偺揹埑栴報偺岦偒偵拲堄偟偰丄乯
|
亅俀[倁乛昩]
|
侾侽.俆. 楙廗乮愊暘夞楬偺岎棳専摙乯
偙偙偱偼丄岎棳夞楬傪暅廗偡傞偨傔偵丄愊暘夞楬偺摦嶌傪岎棳専摙偟傑偡丅
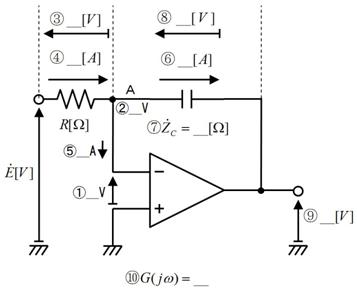
忋恾偺夞楬偵暋慺揹埑 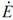 傪壛偊偨偲峫偊偰丄壓昞偺摎棑偵丄昞偺嵟壓晹偵偁傞岓曗偐傜慖傫偩暥帤傗幃傪彂偒崬傫偱岎棳専摙偟丄揱払娭悢傪媮傔偰偔偩偝偄丅
傪壛偊偨偲峫偊偰丄壓昞偺摎棑偵丄昞偺嵟壓晹偵偁傞岓曗偐傜慖傫偩暥帤傗幃傪彂偒崬傫偱岎棳専摙偟丄揱払娭悢傪媮傔偰偔偩偝偄丅
|
斣崋
|
幙栤
|
摎
|
|
嘆
|
亄擖椡偲亅擖椡偺揹埑偼丄晧婣娨偩偐傜丄
|
亄擖椡丂亅擖椡
|
|
嘇
|
俙揰偺揹埑偼丄
|
[倁]
|
|
嘊
|
掞峈偺椉抂揹埑偼丄
|
[倁]
|
|
嘋
|
掞峈R偵棳傟傞揹棳偼丄僆乕儉懃傛傝丄
|
[俙]
|
|
嘍
|
亅擖椡抂巕偵棳傟傞揹棳偼丄
|
[俙]
|
|
嘐
|
僐儞僨儞僒C偵棳傟傞揹棳偼丄僉儖僸懃傛傝丄
|
[俙]
|
|
嘑
|
僐儞僨儞僒C偺暋慺僀儞僺乕僟儞僗偼丄
|
[兌]
|
|
嘒
|
僐儞僨儞僒偺椉抂揹埑偼丄僆乕儉懃傛傝丄
|
[倁]
|
|
嘓
|
弌椡抂巕偺揹埑偼丄
僐儞僨儞僒偺揹埑偺栴報偺岦偒傪峫偊偰丄
|
[倁]
|
|
嘔
|
揱払娭悢偼丄
乮侾亄倞侽倁傪擖椡偟偨偲偒偺弌椡偩偐傜丄乯
|
|
|
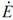 丂 丂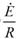 丂 丂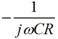 丂 丂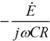 丂 丂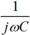 丂 丂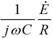 丂侽丂侾丂亜丂亙丂亖 丂侽丂侾丂亜丂亙丂亖
|
侾侽.俇. 摎
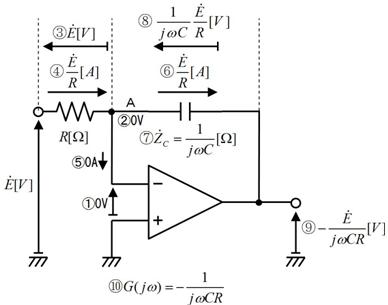
|
斣崋
|
幙栤
|
摎
|
|
嘆
|
亄擖椡偲亅擖椡偺揹埑偼丄晧婣娨偩偐傜丄
|
亄擖椡亖亅擖椡
|
|
嘇
|
俙揰偺揹埑偼丄
|
侽[倁]
|
|
嘊
|
掞峈偺椉抂揹埑偼丄
|
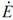 [倁] [倁]
|
|
嘋
|
掞峈偵棳傟傞揹棳偼丄僆乕儉懃傛傝丄
|
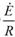 [俙] [俙]
|
|
嘍
|
亅擖椡抂巕偵棳傟傞揹棳偼丄
|
侽 [俙]
|
|
嘐
|
僐儞僨儞僒偵棳傟傞揹棳偼丄僉儖僸懃傛傝丄
|
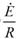 [俙] [俙]
|
|
嘑
|
僐儞僨儞僒偺暋慺僀儞僺乕僟儞僗偼丄
|
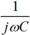 [兌] [兌]
|
|
嘒
|
僐儞僨儞僒偺椉抂揹埑偼丄僆乕儉懃傛傝丄
|
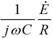 [倁] [倁]
|
|
嘓
|
弌椡抂巕偺揹埑偼丄
僐儞僨儞僒偺揹埑偺栴報偺岦偒傪峫偊偰丄
|
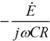 [倁] [倁]
|
|
嘔
|
揱払娭悢偼丄
乮侾亄倞侽倁傪擖椡偟偨偲偒偺弌椡偩偐傜丄乯
|
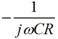
|
偨偲偊偽壓恾偺傛偆偵丄擖椡偑侾昩偵侾倁忋徃偟偰偄傞偲侾倁傪丄侾昩偵俀倁掅壓偟偰偄傞偲亅俀倁傪弌椡偡傞夞楬傪旝暘夞楬偲屇傃傑偡丅偮傑傝丄擖椡偑忋壓偡傞惃偄傪弌椡偡傞夞楬偱偡丅
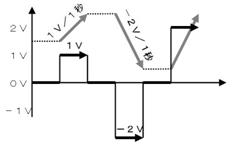
僆儁傾儞僾傪巊偭偨旝暘夞楬傪壓恾偵帵偟傑偡丅
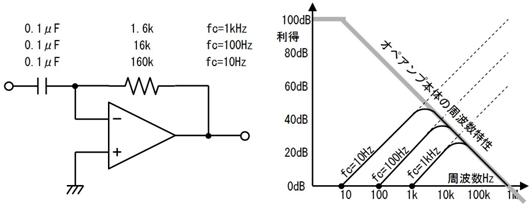
偙偺夞楬偼丄擖椡揹埑偑惃偄椙偔忋徃偡傞掱丄弌椡揹埑偑乽掅偔乿側傞偺偱丄柤慜偙偦乽旝暘夞楬乿偲屇偽傟偰偼偄傑偡偑丄摥偒偼乽斀揮旝暘夞楬乿偱偡丅
摦嶌偺僀儊乕僕偼丄擖椡揹埑偺曄摦偵斾椺偟偨揹棳偑俠偵棳傟丄偦偺揹棳偑俼偵棳傟偰丄偦偺寢壥俼偵敪惗偟偨揹埑偑乮斀揮偟偰乯弌椡揹埑偵側傞丅偦偺偨傔丄擖椡偑堦掕懍搙偱曄摦偡傞偲丄俠偵堦掕偺揹棳偑棳傟偰丄弌椡偵堦掕偺揹埑偑尰傟傞丄偲偄偆傕偺偱偡丅
弌椡揹埑偼丄擖椡揹埑偺忋徃懍搙丄掞峈俼丄僐儞僨儞僒梕検俠偐傜師偺傛偆偵寁嶼偱偒傑偡丄
弌椡揹埑乵倁乶
亖 擖椡揹埑偺崀壓懍搙乵倁乛昩乶
亊 俠
亊 俼
=E1*C1*R1乵倁乶
媡偵俠傗俼偺抣偼丄
俠
亊 俼
亖 弌椡揹埑乵倁乶乛丂擖椡揹埑偺崀壓懍搙乵倁乛昩乶
偙偺夞楬偼忋恾塃懁偺傛偆偵丄廃攇悢偑壓偑傞偲憹暆棪偑掅壓偟傑偡丅憹暆棪偑掅壓偟偰侾攞乮侽倓俛乯偲側傞廃攇悢偼丄
憹暆棪偑侾攞偲側傞廃攇悢
亖侾乛乮俀兾 亊 俠 亊 俼乯乵俫倸乶
=1/2/pi()/C1/R1乵俫倸乶
媡偵俠傗俼偺抣偼丄
俠
亊 俼
亖 侾乛乮俀兾
亊 憹暆棪偑侾攞偲側傞廃攇悢乯
=1/2/pi()/F1
偱寁嶼偡傞偙偲偑偱偒傑偡丅
偝偰旝暘夞楬偼丄忋恾塃偺僌儔僼偵帵偡傛偆偵丄廃攇悢偑忋偑傞偲憹暆棪傕忋徃乮旝暘夞楬偲偟偰摦嶌乯偡傞傕偺偺丄僆儁傾儞僾杮棃偺廃攇悢摿惈傪墇偊偰戝偒偔憹暆偡傞偙偲偼偱偒偢丄崅偄廃攇悢偱偼丄廃攇悢偑忋偑傞偲憹暆棪偑掅壓偟偰偟傑偄傑偆偡丅
偙偺偲偒丄僆儁傾儞僾杮懱偺憹暆棪偑壓偑偭偰峴偔崅偄廃攇悢偱丄忋恾偺僌儔僼偵揰慄偱帵偡傛偆偵丄柍棟偵憹暆棪傪忋偘傛偆偲偡傞偨傔丄旝暘夞楬偼乮敪怳偡傞摍乯晄埨掕偵側傝傗偡偔丄埨掕偝偣傞偨傔偵壓恾偺傛偆偵岺晇偟偰巊偄傑偡丅
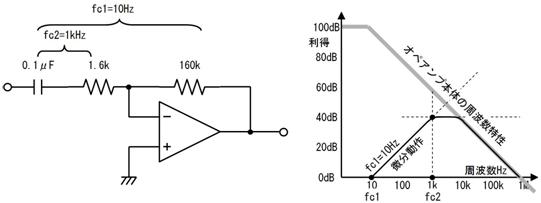
忋恾偺夞楬偱偼丄擖椡偵侾丏俇倠兌傪捛壛偡傞偙偲偱丄忋恾塃懁偺僌儔僼偵帵偡傛偆偵丄侾倠俫倸埲忋偺廃攇悢偱憹暆棪偑忋偑傜側偄傛偆偵偟乮偁傞偄偼丄憹暆棪偺忋尷傪侾侽侽攞偵惂尷偟偰乯丄廃攇悢摿惈傪暯傜偵偟偰偄傑偡丅偙傟偵傛偭偰乽柍棟偵崅偄廃攇悢偺憹暆棪傪忋偘傛偆偲偡傞乿偙偲偑側偔側傝丄夞楬偑埨掕偟傑偡丅
侾侾.侾. 楙廗
壓恾塃偺摿惈傪帩偮丄壓恾嵍偺旝暘夞楬傪丄壓昞偵婰擖偟側偑傜愝寁偟偰偔偩偝偄丅旝暘夞楬偲偟偰摦嶌偡傞廃攇悢偼丄偳偺傛偆側廃攇悢偺斖埻偱偡偐丠
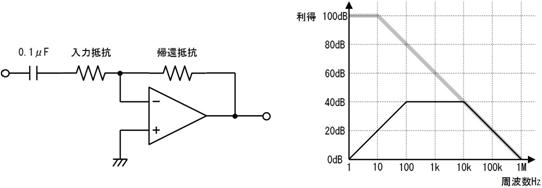
旝暘夞楬偲偟偰摦嶌偡傞廃攇悢偺斖埻丂丂丂丂俫倸乣丂丂丂丂俫倸
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
婣娨掞峈偺抣偼丄侾俫倸偱憹暆棪偑侾攞偲側傝丄僐儞僨儞僒偑侽丏侾兪俥偩偐傜丄
|
俵兌
|
|
嘇
|
擖椡掞峈偺抣偼丄侾侽侽俫倸偐傜忋偱丄棙摼偑暯傜偵側傞偐傜丄
|
倠兌
|
|
嘊
|
廃攇悢偲嫟偵憹暆棪偑忋徃偡傞晹暘偑旝暘夞楬偲偟偰摥偄偰偄傞偐傜丄旝暘夞楬偲偟偰摦嶌偡傞忋尷偺廃攇悢偼丄
|
俫倸
|
侾侾.俀. 摎
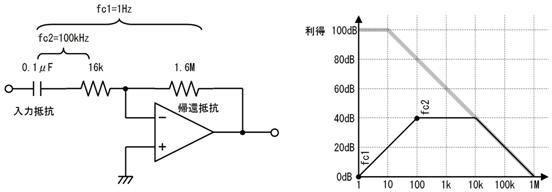
旝暘夞楬偲偟偰摦嶌偡傞斖埻丂丂丂侽俫倸乣丂侾侽侽俫倸
乮侽俫倸偲偼捈棳偺帠乯
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
婣娨掞峈偺抣偼丄侾俫倸偱憹暆棪偑侾攞偲側傝丄僐儞僨儞僒偑侽丏侾兪俥偩偐傜丄=1/2/pi()/1/0.1E-6
|
侾丏俇俵兌
|
|
嘇
|
擖椡掞峈偺抣偼丄侾侽侽俫倸偐傜忋偱丄棙摼偑暯傜偵側傞偐傜丄=1/2/pi()/100/0.1E-6
|
侾俇倠兌
|
|
嘊
|
廃攇悢偲嫟偵憹暆棪偑忋徃偡傞晹暘偑旝暘夞楬偲偟偰摥偄偰偄傞偐傜丄旝暘夞楬偲偟偰摦嶌偡傞忋尷偺廃攇悢偼丄乮僌儔僼偵偼侾俫倸埲壓偺晹暘偼昤偐傟偰偄傑偣傫偑丄偄偔傜掅偄廃攇悢偱傕摦嶌偟傑偡乯
|
侾侽侽俫倸
|
侾俀. 岎棳憹暆夞楬
旕斀揮憹暆婍傗斀揮憹暆婍偼丄捈棳傕憹暆偱偒傞偺偱丄壓恾忋懁乮倐乯偺傛偆偵丄擖椡偵娷傑傟傞捈棳傑偱憹暆偟傑偡丅椺偊偽丄晹壆偺柧傞偝傪應掕偡傞応崌摍偼丄偙偺傛偆偵捈棳傕憹暆偡傞夞楬偑昁梫偱偡丅
媡偵儅僀僋偱廍偭偨壒惡傪憹暆偡傞応崌偼丄捈棳偼慡偔昁梫偑側偔丄媡偵桳奞偱偡丅側偤側傜丄儅僀僋偺弌椡怣崋偼丄俀倁掱搙偺捈棳偺拞偵丄侾倣倁掱搙偺彫偝偄壒惡乮岎棳乯偑擖偭偰偄傞応崌傕懡偄偺偱偡丅偙偺偨傔丄偦偺傑傑侾侽侽侽攞偵憹暆偟偨偺偱偼丄俀侽侽侽倁偺捈棳偺拞偵丄侾倁偺岎棳偑擖偭偰偄傞忬懺偲側傝丄憹暆婍偺弌椡偼怳傝愗偭偰偟傑偄傑偡丅
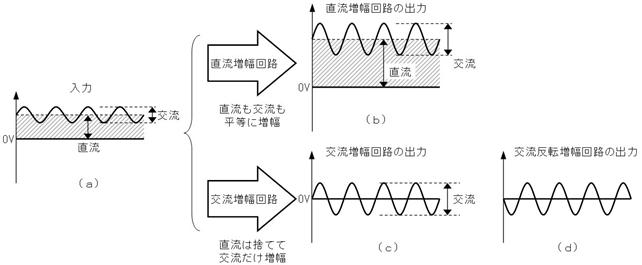
偦偙偱丄忋恾壓懁乮們乯偺傛偆偵丄捈棳偼幪偰嫀偭偰丄岎棳偩偗傪憹暆偡傞夞楬偑巊梡偝傟傑偡丅偙傟偑岎棳憹暆夞楬偱偡丅
忋恾乮們乯傗乮倓乯恾傪尒偰傕丄幚偵偡偭偒傝偟偨弌椡怣崋偑摼傜傟傞偙偲偑暘傝傑偡丅偙偺傛偆偵丄捈棳偑晄梫偱丄媡偵桳奞側応崌偼懡偄偺偱丄岎棳憹暆夞楬偼昿斏偵巊梡偝傟傑偡丅
擖椡偺攇乮忋恾乮倎乯乯偲摨偠僞僀儈儞僌偱弌椡偺攇偑忋壓偡傞乮忋恾乮們乯乯僞僀僾傪乽岎棳憹暆夞楬乿丄媡偺僞僀儈儞僌偱弌椡偺攇偑忋壓偡傞乮忋恾乮倓乯乯僞僀僾偑乽岎棳斀揮憹暆夞楬乿偱偡丅岎棳憹暆夞楬偺応崌丄斀揮偲旕斀揮傪嬫暿偟側偄応崌傕偁傝傑偡丅
侾俁. 斀揮岎棳憹暆婍
壓恾壓懁乮倐乯偵帵偡斀揮岎棳憹暆夞楬偼丄壓恾忋懁乮倎乯偺旝暘夞楬偲摨偠峔惉偱偡丅椉幰偺堘偄偼丄旝暘夞楬偼壓恾乮倎乯偺僌儔僼偵懢慄偱帵偡乽廃攇悢偑忋偑傞偲棙摼傕忋偑傞乿晹暘乮旝暘摦嶌乯傪巊梡偟傑偡偑丄岎棳憹暆婍偼乮倐乯偺僌儔僼偵懢慄偱帵偡乽廃攇悢偑曄傢偭偰傕棙摼偑堦掕乿偺晹暘乮憹暆摦嶌乯傪巊梡偡傞丄偲偄偆揰偱偡丅
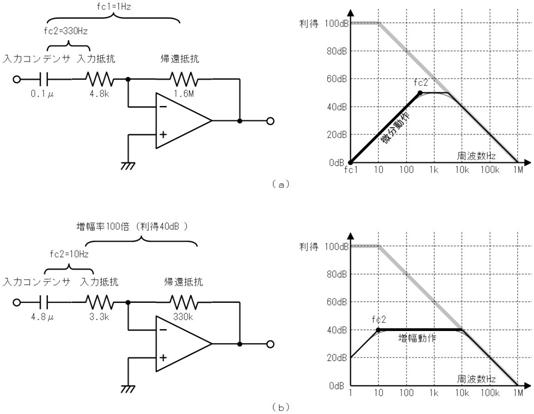
忋恾乮倐乯偺岎棳斀揮憹暆夞楬偺丄僌儔僼偺暯傜側晹暘乮憹暆摦嶌偺晹暘乯偺憹暆棪偼丄斀揮憹暆夞楬偲摨偠傛偆偵峫偊偰丄
憹暆棪
亖 婣娨掞峈
乛 擖椡掞峈
俁俁侽倠
乛 俁丏俁倠
亖 侾侽侽攞乮係侽倓俛乯
=330E3/3.3E3
偲寁嶼偡傞偙偲偑偱偒傑偡丅
傑偨忋恾乮倐乯偺丄僌儔僼偺暯傜側晹暘偺嵍抂偺廃攇悢乮倖俠俀乯偼丄擖椡掞峈俼偲擖椡僐儞僨儞僒俠偺抣偐傜丄
暯傜側晹暘偺嵍抂偺廃攇悢
亖 侾乛乮俀兾
亊 俠
亊 俼乯
侾
乛乮俀兾 亊 係丏俉兪俥 亊 俁丏俁倠兌乯
亖 侾侽俫倸
=1/2/PI()/4.8E-6/3.3E3
偲寁嶼偡傞偙偲偑偱偒傑偡丅
侾侽俫倸埲壓偱偼憹暆棪偑偳傫偳傫壓偑偭偰峴偒傑偡偐傜丄憹暆偟偨偄怣崋偑丄侾侽俫倸傛傝崅偔側偗傟偽偄偗傑偣傫丅
偝偰丄偙偺壓尷偺廃攇悢愝掕偱拲堄偡傞帠偑偁傝傑偡丅壓恾偼侾侽俫倸乮倖俠俀乯晅嬤偺憹暆棪偺僌儔僼傪奼戝偟偨傕偺偱偡丅
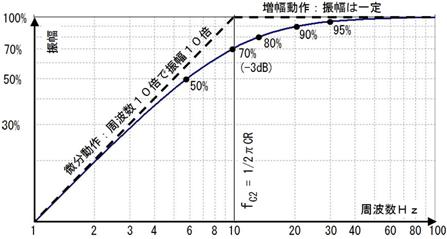
=100*IMABS(IMDIV(1,IMSUM(1,IMDIV(1,COMPLEX(0,F1/10)))))%
F1丗廃攇悢
僇僢僩僆僼廃攇悢嬤朤偱偺憹暆棪
憹暆棪偼丄忋恾偵揰慄偱帵偡傛偆偵丄侾侽俫倸埲忋偱偡偖偵暯傜偵側傞偺偱偼側偔丄幚慄偱帵偡傛偆偵乮妏偵娵傒偑晅偄偰偄傞偨傔乯侾侽俫倸偱傕怳暆偼俈侽亾掱搙乮亅俁倓俛乯偵彫偝偔側偭偰偄傑偡丅偦偟偰俀侽俫倸丄偮傑傝倖俠俀偺俀攞偺廃攇悢偵側偭偰丄傛偆傗偔俋侽亾偵側傝傑偡丅偱偡偐傜丄侾侽俫倸埲忋偺怣崋傪憹暆偡傞偲偒偵丄倖俠俀傪侾侽俫倸偵愝掕偡傞偲丄侾侽俫倸偺怣崋偱憹暆棪偑俁妱尭偲側傝傑偡丅
偲偼偄偊丄傓傗傒偵乮侽丏侽侾俫倸摍偲乯倖俠俀傪嬌傔偰掅偔愝掕偡傞偲乮傕偪傠傫丄掅偄廃攇悢傕妋幚偵憹暆偱偒傑偡偑乯揹尮傪擖傟偨傝働乕僽儖傪愙懕偟偰偐傜丄夞楬偑埨掕偡傞傑偱帪娫偑妡偐傝丄偦偺娫弌椡偑怳傝愗偭偨傝偟傑偡偐傜拲堄偑昁梫偱偡丅
偮傑傝晛捠偺梡搑偱偁傟偽丄倖俠俀偼乽昁梫側怣崋偑庛傑傜側偄斖埻偱丄偱偒傞偩偗崅偔乿愝掕偟偰偍偔偲栤戣偑彮側偄偱偡丅
侾俁.侾. 楙廗
壓恾偺夞楬傪梡偄偰丄憹暆棪侾侽攞偺岎棳斀揮憹暆婍傪嶌傝傑偡丅埖偆怣崋偼侾侽侽俫倸埲忋偱偡偑丄侾侽侽俫倸偺怣崋偱傕憹暆棪傪俋俆亾妋曐偟傑偡丅壓昞偵彂偒崬傒側偑傜丄愝寁偟偰壓偝偄丅
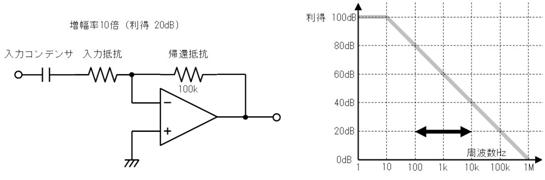
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
憹暆棪傪侾侽攞偵偡傞偨傔偵偼丄擖椡掞峈偺抣偼丄
|
倠兌
|
|
嘇
|
侾侽侽俫倸偺怣崋偱俋俆亾偺怳暆傪妋曐偟偨偄偐傜丄
忋偺乽僇僢僩僆僼廃攇悢嬤朤偱偺憹暆棪乿偺僌儔僼傛傝丄
侾侽侽俫倸偼倖俠偺壗攞偲側偭偰偄傞偐丄
|
攞
|
|
嘊
|
擖椡掞峈偲擖椡僐儞僨儞僒偱寛傑傞倖俠偺抣偼丄
|
俫倸
|
|
嘋
|
擖椡僐儞僨儞僒偺抣偼丄
|
兪俥
|
侾俁.俀. 摎
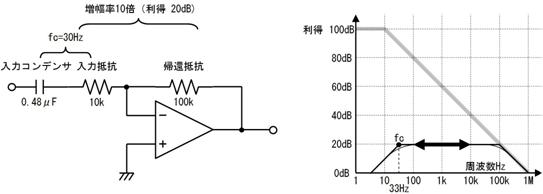
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
憹暆棪傪侾侽攞偵偡傞偨傔偵偼丄擖椡掞峈偺抣偼丄
=100E3/10
|
侾侽倠兌
|
|
嘇
|
侾侽侽俫倸偺怣崋偱俋俆亾偺怳暆傪妋曐偟偨偄偐傜丄
忋偺乽僇僢僩僆僼廃攇悢嬤朤偱偺憹暆棪乿偺僌儔僼傛傝丄
侾侽侽俫倸偼倖俠偺壗攞偲側偭偰偄傞偐丄
婛弌偺乽僇僢僩僆僼廃攇悢嬤朤偱偺憹暆棪乿偺僌儔僼傛傝丄俁攞
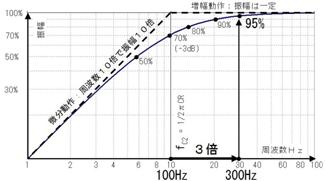
|
俁攞
|
|
嘊
|
擖椡掞峈偲擖椡僐儞僨儞僒偱寛傑傞倖俠偺抣偼丄
侾侽侽俫倸亐俁亖俁俁俫倸
|
俁俁俫倸
|
|
嘋
|
擖椡僐儞僨儞僒偺抣偼丄
=1/2/PI()/10E3/300
|
侽丏係俉兪俥
|
侾係. 扨堦揹尮偺岎棳斀揮憹暆夞楬
壓恾忋懁偼俀揹尮偺俀攞偺岎棳斀揮憹暆夞楬偱偡丅擖椡偑僾儔僗偺偲偒偼弌椡偑儅僀僫僗偵丄擖椡偑儅僀僫僗偺偲偒偼弌椡偑僾儔僗偵側傝丄惓忢偵摦嶌偟偰偄傑偡丅
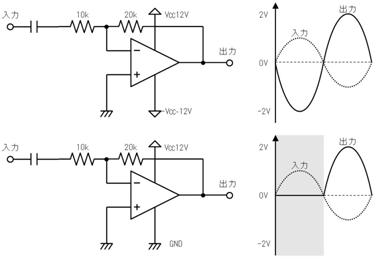
忋恾壓懁偼丄摨偠憹暆婍傪扨揹尮偱巊梡偟偨條巕偱偡丅扨揹尮偱偼儅僀僫僗偺揹埑偑弌椡偱偒側偄偨傔丄擖椡偑僾儔僗偺偲偒偼弌椡偵怣崋偑尰傟傑偣傫丅
扨堦揹尮偱岎棳斀揮憹暆夞楬傪惓偟偔摦嶌偝偣傞偨傔偵丄壓恾偵帵偡傛偆側乽亄擖椡抂巕偵揹埑傪壛偊傞乿夞楬偑椙偔棙梡偝傟傑偡丅偙偺偲偒壛偊傞揹埑傪乽僶僀傾僗揹埑乿偲屇傃傑偡丅
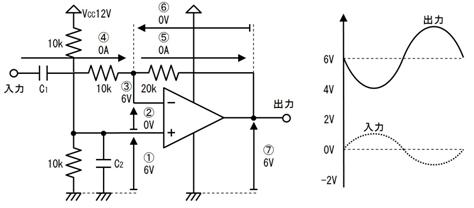
侾係.侾. 妋擣
僶僀傾僗傪壛偊偨扨堦揹尮偺岎棳斀揮憹暆夞楬偺柍怣崋帪偺弌椡揹埑傪丄忋恾傪嶲峫偵壓昞偵彂偒崬傫偱妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡抂巕偺揹埑偼丄
乮揹尮揹埑傪俀杮偺侾侽倠兌偱暘埑偟偰偄傞偐傜丄乯
|
倁
|
|
嘇
|
亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮晧婣娨偺夞楬偩偐傜丄乯
|
倁
|
|
嘊
|
亅擖椡抂巕偺揹埑偼丄
|
倁
|
|
嘋
|
擖椡掞峈偵棳傟傞捈棳偼丄
乮僐儞僨儞僒偼捈棳傪捠偝側偄偐傜丄乯
|
俙
|
|
嘍
|
婣娨掞峈偵棳傟傞捈棳偼丄
乮僆儁傾儞僾偺擖椡偵偼揹棳偑棳傟側偄偐傜丄乯
|
俙
|
|
嘐
|
婣娨掞峈偺椉抂揹埑偼丄
|
倁
|
|
嘑
|
柍怱崋帪偺弌椡揹埑乮弌椡僶僀傾僗揹埑乯偼丄
|
倁
|
侾係.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡抂巕偺揹埑偼丄
乮揹尮揹埑傪俀杮偺侾侽倠兌偱暘埑偟偰偄傞偐傜丄乯
|
俇倁
|
|
嘇
|
亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮晧婣娨偺夞楬偩偐傜丄乯
|
侽倁
|
|
嘊
|
亅擖椡抂巕偺揹埑偼丄
|
俇倁
|
|
嘋
|
擖椡掞峈偵棳傟傞捈棳偼丄
乮僐儞僨儞僒偼捈棳傪捠偝側偄偐傜丄乯
|
侽俙
|
|
嘍
|
婣娨掞峈偵棳傟傞捈棳偼丄
乮僆儁傾儞僾偺擖椡偵偼揹棳偑棳傟側偄偐傜丄乯
|
侽俙
|
|
嘐
|
婣娨掞峈偺椉抂揹埑偼丄
|
侽倁
|
|
嘑
|
柍怱崋帪偺弌椡揹埑乮弌椡僶僀傾僗揹埑乯偼丄
|
俇倁
|
偙偺傛偆偵丄亄擖椡偵僶僀傾僗揹埑傪壛偊傞岎棳斀揮憹暆夞楬偱偼丄弌椡抂巕偺揹埑偼壛偊偨僶僀傾僗揹埑偲摨偠偵側傝傑偡丅
侾係.俁.
楙廗
俠俀偑柍偄偲丄揹尮揹埑偺嬐偐側曄摦偑憹暆偝傟偰丄弌椡偵戝偒偔側偭偰尰傟傑偡丅壓恾偼丄揹尮揹埑偵俀倣倁偺曄摦偺偁傞侾侽侽侽攞偺扨揹尮岎棳斀揮憹暆婍偱偡丅壓恾傪嶲峫偵壓昞偵彂偒崬傫偱丄弌椡揹埑偺曄摦傪媮傔偰偔偩偝偄丅
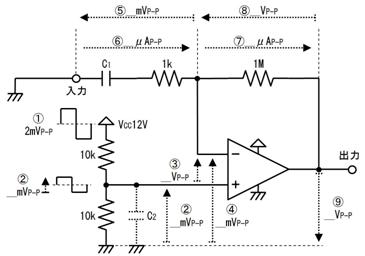
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹尮揹埑偺曄摦偑俀倣倁俹亅俹偁傞偲偟傑偡丅
|
亅
|
|
嘇
|
俠俀偼柍偄偲峫偊偰丄亄擖椡偺揹埑曄摦偼丄
乮揹尮傪俀杮偺侾侽倠兌偱暘埑偟偰偄傞偐傜丄乯
|
倣倁俹亅俹
|
|
嘊
|
亄擖椡抂巕偲亅擖椡抂巕偺揹埑嵎偼丄
|
倁
|
|
嘋
|
亅擖椡抂巕偺揹埑曄摦偼丄
|
倣倁俹亅俹
|
|
嘍
|
擖椡掞峈偺椉抂揹埑偺曄摦偼丄
乮柍怣崋丄偮傑傝擖椡偼傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
倣倁俹亅俹
|
|
嘐
|
擖椡掞峈乮侾倠乯偵棳傟傞揹棳偺曄摦偼丄
乮俠侾偼廫暘戝偒偄偲偟偰丄乯
|
兪俙俹亅俹
|
|
嘑
|
婣娨掞峈乮侾俵乯偵棳傟傞揹棳偺曄摦偼丄
乮僆儁傾儞僾偺擖椡偵偼揹棳偑棳傟側偄偐傜丄乯
|
兪俙俹亅俹
|
|
嘒
|
婣娨掞峈偺椉抂揹埑偺曄摦偼丄
|
倁俹乕俹
|
|
嘓
|
弌椡揹埑偺揹埑曄摦偼丄
|
倁俹亅俹
|
侾係.係. 摎
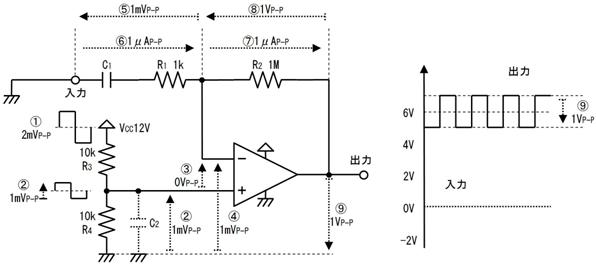
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹尮揹埑偺曄摦偑俀倣倁俹亅俹偁傞偲偟傑偡丅
|
亅
|
|
嘇
|
俠俀偼柍偄偲峫偊偰丄亄擖椡偺揹埑曄摦偼丄
乮揹尮傪俀杮偺侾侽倠兌偱暘埑偟偰偄傞偐傜丄乯
|
侾倣倁俹亅俹
|
|
嘊
|
亄擖椡抂巕偲亅擖椡抂巕偺揹埑嵎偼丄
|
侽倁
|
|
嘋
|
亅擖椡抂巕偺揹埑曄摦偼丄
|
侾倣倁俹亅俹
|
|
嘍
|
擖椡掞峈偺椉抂揹埑偺曄摦偼丄
乮柍怣崋丄偮傑傝擖椡偼傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
侾倣倁俹亅俹
|
|
嘐
|
擖椡掞峈乮侾倠乯偵棳傟傞揹棳偺曄摦偼丄
乮俠侾偼廫暘戝偒偄偲偟偰丄乯
|
侾兪俙俹亅俹
|
|
嘑
|
婣娨掞峈乮侾俵乯偵棳傟傞揹棳偺曄摦偼丄
乮僆儁傾儞僾偺擖椡偵偼揹棳偑棳傟側偄偐傜丄乯
|
侾兪俙俹亅俹
|
|
嘒
|
婣娨掞峈偺椉抂揹埑偺曄摦偼丄
|
侾倁俹乕俹
|
|
嘓
|
弌椡揹埑偺揹埑曄摦偼丄
|
侾倁俹亅俹
|
偙偺傛偆偵丄僶僀傾僗揹埑偺曄摦偼丄憹暆偝傟偰弌椡偵尰傟傑偡丅偱偡偐傜丄憹暆棪偑戝偒偄応崌偼丄梕検偺戝偒側俠俀傪庢傝晅偗偰丄僶僀傾僗揹埑偺曄摦傪彫偝偔偟傑偡丅
偨偲偊埨掕壔揹尮傪巊偭偰偄偰傕丄揹尮偐傜夞楬傑偱偺攝慄偺乮揹慄偺掞峈抣偺乯塭嬁摍偱丄悢倣倁偺曄摦偼偟偽偟偽惗偠傑偡丅偱偡偐傜丄憹暆棪偑戝偒偄応崌偼丄俼俁乛乛俼係偲俠俀偱寛傑傞帪掕悢冄偑丄侽丏侾乣侾昩偵側傞傛偆偵俠俀傪寛傔傞応崌偑戝敿偱偡丅乮偦傟埲忋戝偒偄偲丄夞楬偑埨掕偡傞傑偱偵帪娫偑妡偐傝傑偡乯
冄
亖乮 俼俁 乛乛
俼係 乯亊 俠俀
亖 侽丏侾
乣 侾 丂乮乽乛乛乿偼暲楍崌惉掞峈偺儅乕僋乯
俤倶們倕倢偱偼丄=1/(1/R3+1/R4)*C2 偑
侽丏侾乣侾昩
俠俀偺梕検偼丄
俠俀
亖 侽丏侾乣侾
亐 乮
俼俁 乛乛 俼係
乯
俤倶們倕倢偱偼丄=T1*(1/R3+1/R4)
侾係.俆. 楙廗
忋恾偺夞楬偱丄帪掕悢冄偑侾昩偵側傞傛偆偵丄俠俀傪寛掕偟偰壓偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俼俁偲俼係偺暲楍崌惉掞峈偼丄
|
倠兌
|
|
嘇
|
帪掕悢偑侾昩偲偡傞偐傜丄俠俀偺抣偼丄
|
兪俥
|
侾係.俇. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俼俁偲俼係偺暲楍崌惉掞峈偼丄
=1/(1/10E3+1/10E3)
|
俆倠兌
|
|
嘇
|
帪掕悢偑侾昩偲偡傞偐傜丄俠俀偺抣偼丄
=1/5E3
|
俀侽侽兪俥
|
侾俆. 侾師偺僼傿儖僞
廃攇悢偵傛偭偰棙摼摍偑曄壔偡傞夞楬傪僼傿儖僞偲屇傃傑偡丅晄梫側廃攇悢偺怣崋傪庢傝彍偄偨傝丄婓朷偺怣崋偩偗傪慖戰偟偨傝丄攇宍傪惍偊偨傝丄條乆側梡搑偱巊傢傟傑偡丅
婛偵愢柧偟偨愊暘夞楬丄旝暘夞楬丄懷堟惂尷丄岎棳憹暆夞楬傕丄侾師偺僼傿儖僞偺堦庬偱偡丅偙偺傛偆偵侾師偺僼傿儖僞偵偼丄懡偔偺庬椶偑偁傝傑偡偑丄杦偳偺応崌侾偮偺僆儁傾儞僾偱峔惉偱偒傑偡丅壓恾偵戙昞揑側侾師僼傿儖僞偺夞楬偲廃攇悢摿惈傪帵偟傑偡丅
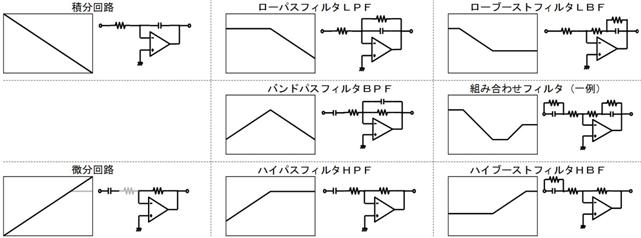
忋恾偺忋抜偑愊暘宯偺僼傿儖僞丄壓抜偑旝暘宯偺僼傿儖僞偱丄拞抜偼愊暘偲旝暘憃曽偺惈幙傪旛偊偨僼傿儖僞偱偡丅嵍偐傜塃偵峴偔偵廬偭偰慺巕偑捛壛偝傟丄偦傟偵傛偭偰廃攇悢摿惈偺愜傟嬋偑傝売強偑憹偊偰備偒傑偡丅
侾師偺僼傿儖僞偼丄偄偢傟傕俇倓俛乛倧們倲乮廃攇悢侾侽攞偱憹暆棪侾侽攞乮偁傞偄偼侾侽暘偺侾乯乯偺妱崌偱偟偐丄憹暆棪偑曄壔偟傑偣傫丅偙傟埲忋媫寖偵曄壔偝偣偨偄偲偒偼丄侾師偺僼傿儖僞傪暋悢愙懕偟偨傝丄俀師埲忋偺僼傿儖僞傪棙梡偟傑偡丅
偡偱偵愢柧偟偨壓恾偺乽懷堟惂尷乿偺夞楬偑丄幚偼侾師儘乕僷僗僼傿儖僞偱偡丅

忋偺夞楬偱偼丄婣娨夞楬乮屻傠懁乯偺俠偲俼偱寛傑傞廃攇悢侾乛俀兾俠俼乵俫倸乶傛傝崅偄廃攇悢偱丄憹暆棪偑掅壓偟偰峴偒傑偟偨丅
壓恾傪梡偄偰丄偦偺棟桼傪愢柧偟傑偡丅壓恾偱偼婣娨夞楬偺俠偲俼偱寛傑傞廃攇悢偼侾倠俫倸偱偡丅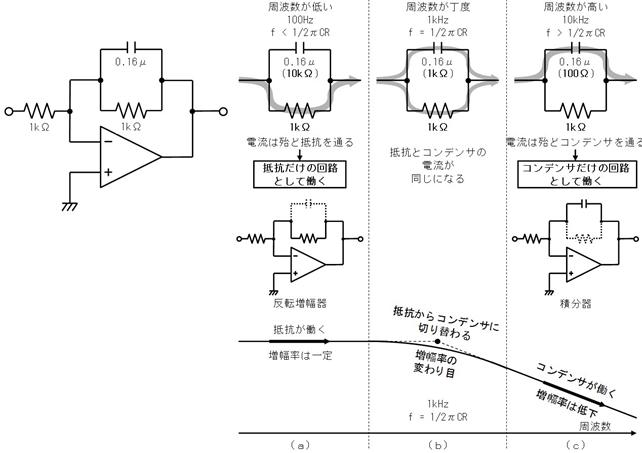
忋恾乮倎乯偵帵偡丄廃攇悢偑侾侽侽俫倸偲掅偄応崌偼丄掞峈乮侾倠兌乯偵斾傋偰僐儞僨儞僒偼侾侽倠兌偲戝偒偄偺偱丄揹棳偼杦偳掞峈傪捠傝傑偡丅偙偺偨傔丄僐儞僨儞僒偼柍偄偲峫偊偰傕偐傑偄傑偣傫丅廬偭偰丄偙偺廃攇悢偱偼掞峈偩偗偺夞楬偲側傝丄乮斀揮憹暆夞楬偲偟偰摦嶌偟偰乯憹暆棪偼廃攇悢偵傛傜偢堦掕偱偡丅
忋恾乮們乯偵帵偡丄廃攇悢偑侾侽倠俫倸偲崅偄応崌偼丄掞峈乮侾倠兌乯偵斾傋偰僐儞僨儞僒偑侾侽侽兌偲彫偝偄偺偱丄揹棳偼杦偳僐儞僨儞僒傪捠傝傑偡丅偙偺偨傔丄掞峈偼柍偄偲峫偊偰傕偐傑偄傑偣傫丅廬偭偰丄偙偺廃攇悢偱偼僐儞僨儞僒偩偗偺夞楬偲側傝丄乮愊暘夞楬偲偟偰摦嶌偟偰乯憹暆棪偼廃攇悢偑崅偄掱尭彮偟偰峴偒傑偡丅
乮倎乯偲乮們乯偺曄傢傝栚偑丄忋恾乮倐乯偱偡丅偙偺偲偒丄掞峈偲僐儞僨儞僒偺僀儞僺乕僟儞僗乮偺戝偒偝乯偑摍偟偔側傝丄掞峈偲僐儞僨儞僒偵摨偠揹棳偑棳傟傑偡丅
掞峈偺僀儞僺乕僟儞僗偼俼乵兌乶偱丄僐儞僨儞僒偺僀儞僺乕僟儞僗乮偺戝偒偝乯偑侾乛俀兾倖俠乵兌乿偱偟偨偐傜丄椉曽偑摨偠偵側傞偲偒丄偮傑傝俼亖侾乛俀兾倖俠偲側傞廃攇悢偼倖亖侾乛俀兾俠俼偲寁嶼偡傞偙偲偑偱偒傑偡丅
偙偺傛偆偵丄廃攇悢偑曄壔偟偰丄僐儞僨儞僒偺僀儞僺乕僟儞僗偑掞峈傛傝廫暘戝偒偔丄偁傞偄偼廫暘彫偝偔側傞偲丄偳偪傜偐堦曽偩偗偵揹棳偑棳傟丄偦偆偱側偄曽偼乽柍偄乿偲峫偊偰傕椙偄忬懺偵側傝傑偡丅偙傟偵傛偭偰丄傑傞偱夞楬傪愗傝懼偊偨傛偆偵側傝丄斀揮憹暆婍偩偭偨摦嶌偑丄崅偄廃攇悢偱偼愊暘夞楬偺摦嶌偵愗傝懼傢傞偺偱偡丅
侾俇.侾. 楙廗
壓恾偺丄幷抐廃攇悢倖俠係係侽俫倸丄憹暆棪俀攞偺侾師儘乕僶僗僼傿儖僞偺俠俼偺抣傪丄壓昞偵婰擖偟側偑傜寛掕偟偰偔偩偝偄丅
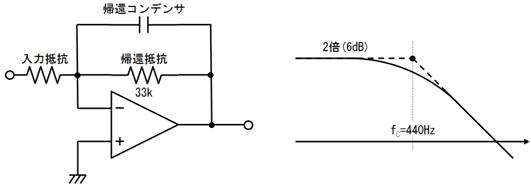
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
憹暆棪傪俀攞偵偡傞偨傔偵偼丄擖椡掞峈偺抣偼丄
|
倠兌
|
|
嘇
|
幷抐廃攇悢倖俠傪係係侽俫倸偵偡傞偨傔偵丄婣娨僐儞僨儞僒偺抣偼丄
|
兪俥
|
侾俇.俀. 摎
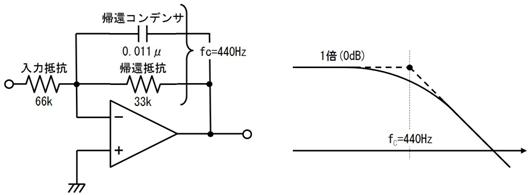
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
憹暆棪傪俀攞偵偡傞偨傔偵偼丄擖椡掞峈偺抣偼丄
|
俇俇倠兌
|
|
嘇
|
幷抐廃攇悢倖俠傪係係侽俫倸偵偡傞偨傔偵丄婣娨僐儞僨儞僒偺抣偼丄
=1/2/PI()/33E3/440
|
侽丏侽侾侾兪俥
|
侾俈. 侾師僴僀僷僗僼傿儖僞俫俹俥
偡偱偵愢柧偟偨壓恾偺乽岎棳斀揮憹暆夞楬乿偑丄幚偼侾師僴僀僷僗僼傿儖僞偱偡丅
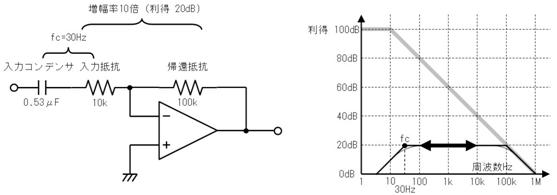
忋偺夞楬偱偼丄擖椡夞楬乮慜懁乯偺俠偲俼偱寛傑傞廃攇悢侾乛俀兾俠俼乵俫倸乶傛傝掅偄廃攇悢偱丄廃攇悢偑壓偑傞掱憹暆棪偑掅壓乮廃攇悢偑忋偑傞掱憹暆棪偑忋徃乯偟偰峴偒傑偟偨丅
摦嶌偺巇慻傒偼俴俹俥偲摨條偵慜懁偺乮擖椡夞楬偺乯掞峈偲僐儞僨儞僒偺僀儞僺乕僟儞僗傪斾傋偰峫偊傞偙偲偑偱偒傑偡丅壓恾傪梡偄偰愢柧偟傑偡丅壓恾偱偼擖椡夞楬偺俠偲俼偱寛傑傞廃攇悢偼侾倠俫倸偱偡丅
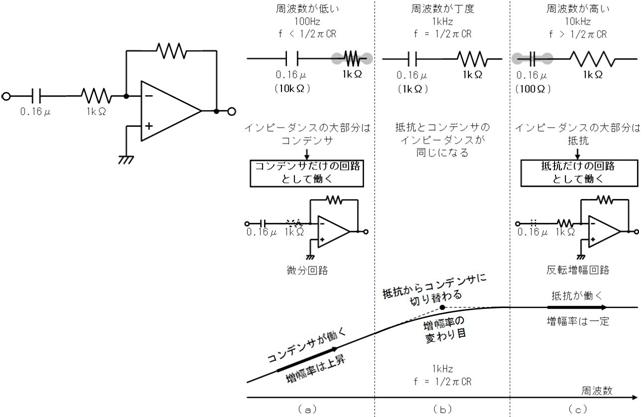
忋恾乮倎乯偵帵偡丄廃攇悢偑掅偄応崌偼丄掞峈偵斾傋偰僐儞僨儞僒偺僀儞僺乕僟儞僗偑戝偒偔側傝丄掞峈偼僔儑乕僩偟偰偄傞偲峫偊傞偙偲偑偱偒丄乽柍偄乿偲峫偊偰偐傑偄傑偣傫丅廬偭偰丄偙偺廃攇悢偱偼僐儞僨儞僒偩偗偺夞楬偲側傝丄乮旝暘夞楬偲偟偰摦嶌偟偰乯廃攇悢偑忋偑傞偲憹暆棪偑忋徃偟偰峴偒傑偡丅
忋恾乮們乯偺廃攇悢偑崅偄応崌偼丄掞峈偵斾傋偰僐儞僨儞僒偺僀儞僺乕僟儞僗偑彫偝偄偺偱丄僐儞僨儞僒偼僔儑乕僩偟偰偄傞偲峫偊傞偙偲偑偱偒丄乽柍偄乿偲峫偊偰偐傑偄傑偣傫丅廬偭偰丄偙偺廃攇悢偱偼掞峈偩偗偺夞楬偲側傝丄乮斀揮憹暆夞楬偲偟偰摦嶌偟偰乯憹暆棪偼廃攇悢偑曄壔偟偰傕堦掕偱偡丅
掞峈抣偲僐儞僨儞僒偺僀儞僺乕僟儞僗偑摨偠偵側傞丄忋恾乮倐乯応崌偑丄旝暘夞楬偑斀揮憹暆夞楬偵愗傝懼傢傞嫬栚偱偡丅偙偺偲偒丄俼乵兌乶亖侾乛俀兾倖俠乵兌乿偲側傝丄嫬栚偺廃攇悢偼丄倖亖侾乛俀兾俠俼偲寁嶼偡傞偙偲偑偱偒傑偡丅
侾俉. 侾師僶儞僪僷僗僼傿儖僞俛俹俥
壓恾偵帵偡偲偍傝丄侾師僶儞僪僷僗僼傿儖僞乮俛俹俥乯偼丄侾師俴俹俥偲侾師俫俹俥傪慻傒崌傢偣偨傕偺偱偡丅
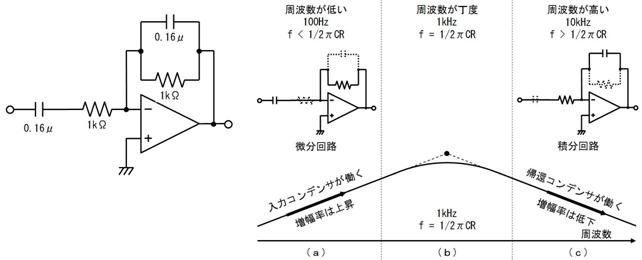
忋恾乮倎乯偵帵偡傛偆偵廃攇悢偺掅偄斖埻偱偼丄擖椡夞楬乮俠俼捈楍乯偱偼丄掞峈偵斾傋偰僐儞僨儞僒偺僀儞僺乕僟儞僗偑崅偔丄掞峈偼僔儑乕僩偟偰偄傞偲峫偊傞偙偲偑偱偒丄擖椡僐儞僨儞僒偺傒偺夞楬偲尒傞偙偲偑偱偒傑偡丅傑偨婣娨夞楬乮俠俼暲楍乯偱偼丄僐儞僨儞僒偺僀儞僺乕僟儞僗偑崅偔丄揹棳偺戝敿偼掞峈偵棳傟傞偨傔丄掞峈偺傒偺夞楬偲尒傞偙偲偑偱偒傑偡丅偙偺偨傔丄廃攇悢偺掅偄晹暘偱偼旝暘夞楬偲偟偰摦嶌偟丄廃攇悢偺忋徃偵敽偭偰憹暆棪偑忋徃偟偰峴偒傑偡丅
忋恾乮們乯偵帵偡傛偆偵廃攇悢偺崅偄斖埻偱偼丄擖椡夞楬乮俠俼捈楍乯偱偼丄僐儞僨儞僒偺僀儞僺乕僟儞僗偑掅偔丄僔儑乕僩偟偰偄傞偲峫偊傞偙偲偑偱偒丄擖椡掞峈偺傒偺夞楬偲尒傞偙偲偑偱偒傑偡丅傑偨丄婣娨夞楬乮俠俼暲楍乯偱偼丄僐儞僨儞僒偺僀儞僺乕僟儞僗偑掅偔丄揹棳偺戝敿偼僐儞僨儞僒偵棳傟傞偨傔丄僐儞僨儞僒偺傒偺夞楬偲尒傞偙偲偑偱偒傑偡丅偙偺偨傔丄廃攇悢偺崅偄晹暘偱偼愊暘夞楬偲偟偰摦嶌偟丄廃攇悢偺忋徃偵敽偭偰憹暆棪偑掅壓偟偰峴偒傑偡丅
擖椡夞楬偲婣娨夞楬偺憃曽偱丄掞峈抣偲僐儞僨儞僒偺僀儞僺乕僟儞僗偑摨偠偵側傞丄忋恾乮倐乯偲偒偑丄旝暘夞楬偑愊暘夞楬偵愗傝懼傢傞嫬栚偱偡丅偙偺偲偒擖椡夞楬偲婣娨夞楬偺奺俠俼偑摨偠僀儞僺乕僟儞僗丄偮傑傝丄俼乵兌乶亖侾乛俀兾倖俠乵兌乿偲側傝丄偙傟傛傝丄嫬栚偺廃攇悢偼丄倖亖侾乛俀兾俠俼偲寁嶼偡傞偙偲偑偱偒傑偡丅
侾俉.侾. 楙廗
壓恾偺丄拞怱廃攇悢倖俠係係侽俫倸丄憹暆棪侾侽攞偺侾師僶儞僪僷僗僼傿儖僞偺俠俼偺抣傪丄壓昞偵婰擖偟側偑傜寛掕偟偰偔偩偝偄丅
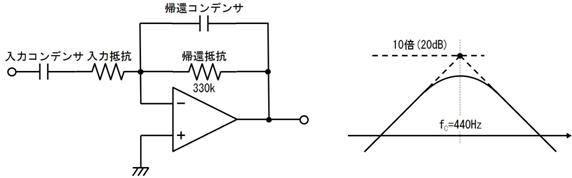
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
憹暆棪傪侾侽攞偵偡傞偨傔偵偼丄擖椡掞峈偺抣偼丄
|
倠兌
|
|
嘇
|
拞怱廃攇悢倖俠傪係係侽俫倸偵偡傞偨傔偵丄婣娨僐儞僨儞僒偺抣偼丄
|
兪俥
|
|
嘊
|
拞怱廃攇悢倖俠傪係係侽俫倸偵偡傞偨傔偵丄擖椡僐儞僨儞僒偺抣偼丄
|
兪俥
|
侾俉.俀. 摎
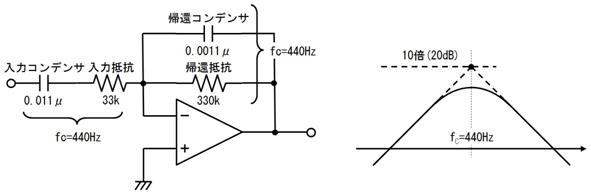
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
憹暆棪傪侾侽攞偵偡傞偨傔偵偼丄擖椡掞峈偺抣偼丄
=33E3*10
|
俁俁倠兌
|
|
嘇
|
拞怱廃攇悢倖俠傪係係侽俫倸偵偡傞偨傔偵丄婣娨僐儞僨儞僒偺抣偼丄
=1/2/PI()/330E3/440
|
侽丏侽侽侾侾兪俥
|
|
嘊
|
拞怱廃攇悢倖俠傪係係侽俫倸偵偡傞偨傔偵丄擖椡僐儞僨儞僒偺抣偼丄
=1/2/PI()/33E3/440
|
侽丏侽侾侾兪俥
|
侾俋. 侾師慻傒崌傢偣僼傿儖僞乮摦嶌偺僀儊乕僕乯
慻傒崌傢僼傿儖僞偼丄擖椡夞楬傗婣娨夞楬偵丄傛傝懡偔偺俠俼偑巊梡偝傟丄廃攇悢摿惈偵暋悢偺愜傟嬋偑傝偑偁傞夞楬偱偡丅偙偙偱偼丄惓妋側寁嶼偺曽朄偱偼側偔丄摦嶌偺僀儊乕僕傪愢柧偟傑偡丅
壓恾偺傛偆偵丄婣娨懁偵俠俼夞楬傪愝偗偰丄廃攇悢摿惈偑壗搙傕愜傟嬋偑傝偮偮丄塃壓傝偲側傞僼傿儖僞傕僆儁傾儞僾侾偮偱嶌傞偙偲偑偱偒傑偡丅
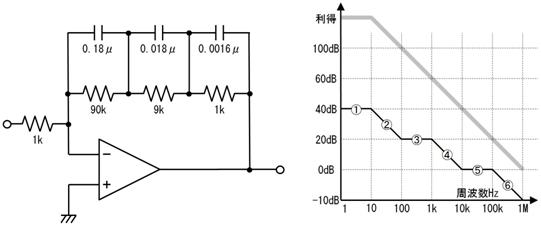
忋恾塃懁偺僌儔僼偵嘆乣嘐偵帵偡丄偦傟偧傟偺廃攇悢偱偺僐儞僨儞僒偺僀儞僺乕僟儞僗傪丄壓恾嘆乣嘐偵帵偟傑偡丅
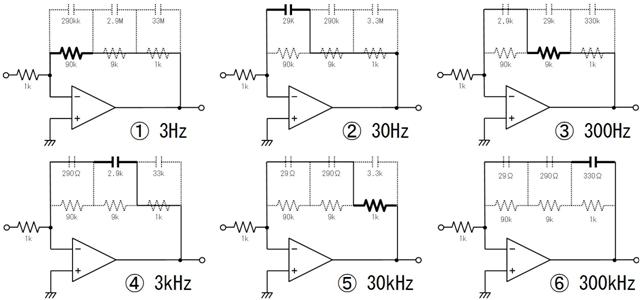
忋恾偵懢慄偱帵偡傛偆偵丄僀儞僺乕僟儞僗偺曄壔偵傛偭偰丄庡栶偲偟偰嶌梡偡傞慺巕偑岎戙偟丄憹暆夞楬偲偟偰偺摦嶌偲丄愊暘夞楬偲偟偰偺摦嶌偑岎屳偵愗傝懼傢傝傑偡丅
偙傟偲偼暿偵壓恾偺傛偆偵丄擖椡懁偵俠俼夞楬傪愝偗偰丄廃攇悢摿惈偑壗搙傕愜傟嬋偑傝偮偮丄塃忋傝偲側傞僼傿儖僞傕僆儁傾儞僾侾偮偱嶌傞偙偲偑偱偒傑偡丅
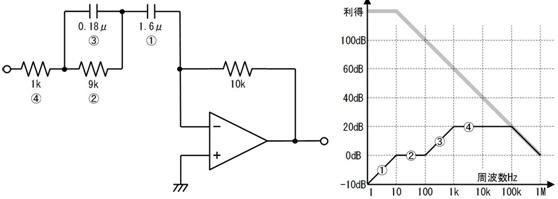
忋恾偱偼丄廃攇悢偑崅偔側傞偵廬偭偰丄嘆嘇嘊嘋偺弴偱庡栶偵側傞慺巕偑愗傝懼傢傝丄忋恾塃懁偺僌儔僼偵帵偡廃攇悢摿惈偑摼傜傟傑偡丅
偝傜偵暿偺夞楬偱偼丄壓恾偺傛偆偵丄擖椡懁偵傕婣娨懁偵傕俠俼夞楬傪愝偗偰丄廃攇悢摿惈偑壗搙傕愜傟嬋偑傝偮偮丄忋壓偡傞僼傿儖僞傕僆儁傾儞僾侾偮偱嶌傞偙偲偑偱偒傑偡丅庡栶偲側傞慺巕偑曄壔偟偰丄斀揮憹暆夞楬丄旝暘夞楬丄愊暘夞楬偵摦嶌偑愗傝懼傢傝傑偡丅
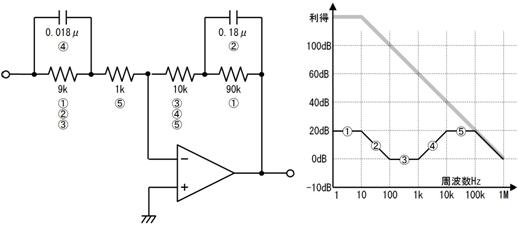
忋恾偺傛偆側慻傒崌傢偣僼傿儖僞偼堦尒暋嶨偵尒偊傑偡偑丄婡擻偡傞慺巕偑弴偵愗傝懼傢傞偩偗偱丄摦嶌偼扨弮偱偡丅
壓恾嵍懁偺廃攇悢摿惈傪帩偮丄壓恾塃懁偺慻傒崌傢偣僼傿儖僞傪椺偵丄慺巕偺愗傝懼傢傝偲夞楬偺摦嶌傪丄廃攇悢偺掅偄応崌嘆偐傜丄廃攇悢偺崅偄応崌嘍傊偲岦偐偭偰丄壓昞偱愢柧偟傑偡丅
廃攇悢偑崅偔側傞偲乮俠偺僀儞僺乕僟儞僗偑師戞偵崅偔側傞偨傔乯丄俠偲俼偑暲楍側晹暘偱偼乽俠偑庡偵揹棳傪棳偡偨傔丄俼傪柍帇偱偒傞乿傑偨丄俠偲俼偑捈楍側晹暘偱偼乽俠偑抁棈偡傞偨傔丄俼偩偗偑婡擻偡傞乿偲峫偊傑偡丅
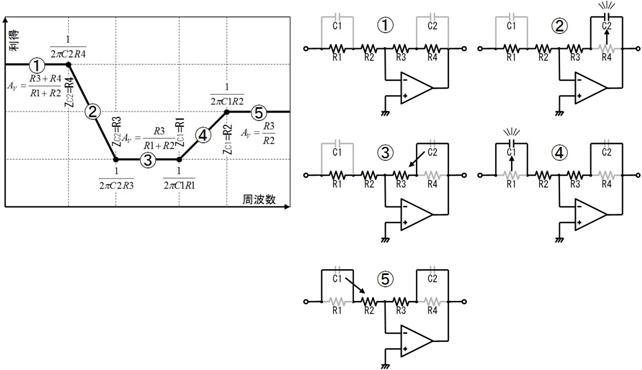
|
斣崋
|
嘆
|
嘇
|
嘊
|
嘋
|
嘍
|
|
廃攇悢
|
掅偄
|
仺
|
仺
|
仺
|
崅偄
|
|
慺巕偺
僀儞僺乕僟儞僗
|
C2亜R4
|
C2亙R4
|
C2亙R4
|
C2亙R4
|
C2亙R4
|
|
C2亜R3
|
C2亜R3
|
C2亙R3
|
C2亙R3
|
C2亙R3
|
|
C1亜R1
|
C1亜R1
|
C1亜R1
|
C1亙R1
|
C1亙R1
|
|
C1亜R2
|
C1亜R2
|
C1亜R2
|
C1亜R2
|
C1亙R2
|
|
愢柧
|
廃攇悢偑廫暘掅偄帪丄俠侾俠俀偼杦偳揹棳傪棳偟傑偣傫丅偙偺偨傔夞楬恾嘆偺傛偆偵丄掞峈偩偗偺憹暆夞楬偲偟偰摦嶌偟丄廃攇悢摿惈偼僌儔僼嘆偺傛偆偵暯傜偵側傝傑偡丅
|
俠俀偺僀儞僺乕僟儞僗偑俼係傛傝彫偝偔側傞偲丄揹棳偼庡偵俠俀傪棳傟丄夞楬恾嘇偺傛偆偵婣娨夞楬偵俠偺擖偭偨愊暘夞楬偲偟偰摦嶌偟丄廃攇悢摿惈偼僌儔僼嘇偺傛偆偵丄塃壓傝偲側傝傑偡丅
|
俠俀偺僀儞僺乕僟儞僗偑俼俁傛傝彫偝偔側傞偲丄婣娨夞楬偺庡側僀儞僺乕僟儞僗偼俼俁偲側傝丄夞楬恾嘊偺傛偆偵憹暆夞楬偲偟偰摦嶌偟丄廃攇悢摿惈偼僌儔僼嘊偺傛偆偵暯傜偵側傝傑偡丅
|
俠侾偺僀儞僺乕僟儞僗偑俼侾傛傝彫偝偔側傞偲丄揹棳偼庡偵俠侾傪棳傟丄夞楬恾嘋偺傛偆偵擖椡夞楬偵俠偺擖偭偨旝暘夞楬偲偟偰摦嶌偟丄廃攇悢摿惈偼僌儔僼嘋偺傛偆偵丄塃忋傝偲側傝傑偡丅
|
俠侾偺僀儞僺乕僟儞僗偑俼俀傛傝彫偝偔側傞偲丄擖椡夞楬偺庡側僀儞僺乕僟儞僗偼俼俀偲側傝丄夞楬恾嘍偺傛偆偵憹暆夞楬偲偟偰摦嶌偟丄廃攇悢摿惈偼僌儔僼嘍偺傛偆偵暯傜偵側傝傑偡丅
|
|
摦嶌
|
憹暆夞楬
|
愊暘夞楬
|
憹暆夞楬
|
旝暘夞楬
|
憹暆夞楬
|
|
憹暆棪[攞]
|
(R3+R4)/(R1+R2)
|
|
R3/(R1+R2)
|
|
R3/R2
|
|
廃攇悢[Hz]
|
亅
|
1 / (2兾C2R4)
|
1 / (2兾C2R3)
|
1 / (2兾C1R1)
|
1 / (2兾C1R2)
|
亅
|
|
|
|
|
|
|
|
|
|
|
|
俀侽. 侾師慻傒崌傢偣僼傿儖僞乮帠椺専摙乯
幚嵺偺夞楬偱偼丄庡栶偵側傞慺巕偑偼偭偒傝愗傝懼傢傜偢丄旝柇側姶偠偱堏峴偟偰峴偔応崌傕懡偄偱偡丅椺偊偽壓恾偼丄埨暔僆乕僨傿僆偱掅壒偲崅壒傪憹嫮偡傞栚揑偱棙梡偟偨夞楬偱偡丅乮弌暔偺僇僫儖宆僀儎儂儞偱乮壒怓偼慺揋側偺偵乯掅壒偲崅壒偑庛偐偭偨偺偱嶌傝傑偟偨乯
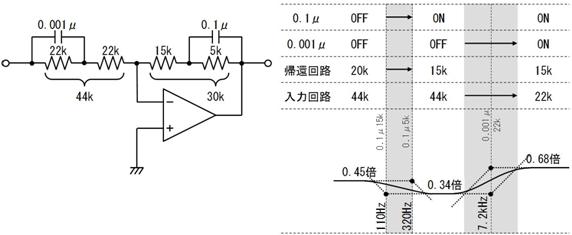
偝偰忋恾嵍懁偺夞楬恾傪尒傞偲丄擖椡夞楬偺俀杮偺掞峈偑摨偠抣偱偡偟丄婣娨夞楬偺俀杮偺掞峈傕俁攞掱搙偟偐嵎偑偁傝傑偣傫丅偦偺偨傔丄乽摦嶌偺僀儊乕僕乿偱愢柧偟偨傛偆偵丄廃攇悢偵傛偭偰慺巕傪柍帇偡傞栿偵峴偒傑偣傫丅
偙偺傛偆側応崌丄傑偢丄忋恾塃懁偺昞偺傛偆偵丄僐儞僨儞僒傪廃攇悢偱俷俶乛俷俥俥偡傞僗僀僢僠偩偲峫偊偰憹暆棪傪寁嶼偟傑偡丅
偮傑傝丄僐儞僨儞僒偑偳偪傜傕俷俥俥乮偲偰傕掅偄廃攇悢乯偱偼憹暆棪偼侽丏係俆攞丄廃攇悢偑彮偟忋偑偭偰侽丏侾兪偑俷俶偵側傞偲侽丏俁係攞丄偝傜偵廃攇悢偑忋偑偭偰椉曽偲傕俷俶偵側傞偲侽丏俇俉攞丄偲媮傔傑偡丅
偦偺屻偱丄僐儞僨儞僒偲掞峈偱寛傑傞廃攇悢傪偦傟偧傟寁嶼偟丄乮俁俀侽俫倸丄侾侾侽俫倸丄俈丏俀倠俫倸丄俈丏俀倠俫倸乯憹暆棪偑曄壔傪巒傔傞廃攇悢偲偟偰丄忋恾塃壓偺傛偆偵丄僌儔僼偵彂偒崬傒傑偡丅
婣娨夞楬偱偼丄乽曄壔傪巒傔傞廃攇悢乿偑俁俀侽俫倸丆乽曄壔傪廔偊傞廃攇悢乿偑侾侾侽俫倸偲丄乽巒傔乿偲乽廔傝乿偺抣偑媡偵側偭偰偄傑偡丅偙傟偼丄憹暆棪偺抜嵎偑彫偝偄偨傔偱偡丅
擖椡夞楬偱傕丄乽曄壔傪巒傔傞廃攇悢乿偑俈丏俀倠俫倸丆乽曄壔傪廔偊傞廃攇悢乿偑俈丏俀倠偲摨偠偱偡偑丄偙傟傕丄乮婣娨夞楬掱偱偼柍偄偗傟偳乯憹暆棪偺抜嵎偑彫偝偄偨傔偱偡丅
偙偺傛偆偵偟偰僌儔僼偵彂偒崬傫偩憹暆棪偺捈慄偺娫傪捠傞傛偆偵丄側偩傜偐偵嬋慄傪昤偗偽丄戝懱偺廃攇悢摿惈傪抦傞偙偲偑偱偒傑偡丅
傕偪傠傫丄岎棳夞楬偺抦幆傪巊偭偰揱払娭悢傪媮傔丄俤倶們倕倢偱惓妋柍斾側廃攇悢摿惈傪昤偔偙偲傕偱偒傑偡丅偟偐偟丄妛峑偺儗億乕僩埲奜偱偼丄偦傟掱偺惛枾偝偑媮傔傜傟偨帠偼偁傝傑偣傫丅
俀侾. 僔儏儈僢僩丒僩儕僈乮斀揮乯
僔儏儈僢僩僩儕僈偼敪柧幰偺乮僆僢僩乕丒僔儏儈僢僩偝傫乯偵偪側傫偩柤慜偱偡丅恄宱偺尋媶傪偟偰偄偨僔儏儈僢僩偝傫偼丄巋寖偑堦掕偺儗儀儖傪挻偊側偄偲斀墳乮僩儕僈乯偟側偄偲偄偆恄宱偺惈幙傪揹巕夞楬偱柾曧偡傞偨傔偵丄偙偺夞楬傪敪柧偟傑偟偨丅
壓恾偵僔儏儈僢僩僩儕僈偺椺傪帵偟傑偡丅乮偙偙偱偼俆倁扨堦揹尮偱峫偊偰偄傑偡乯亅擖椡偵怣崋偑擖椡偝傟偨斀揮僐儞僷儗乕僞偺夞楬偲帡偰偄傑偡偑丄僔儏儈僢僩僩儕僈偱偼丄弌椡偐傜亄擖椡偵岦偐偭偰乽惓婣娨乿掞峈偑捛壛偝傟偰偄傑偡丅
亅擖椡偵弌椡揹埑偑夞傝崬傓乽晧婣娨乿偱偼丄亄擖椡偲亅擖椡偺揹埑偑摍偟偔側傝傑偟偨偑丄惓婣娨偱偼偙偺尰徾偼惗偠傑偣傫丅
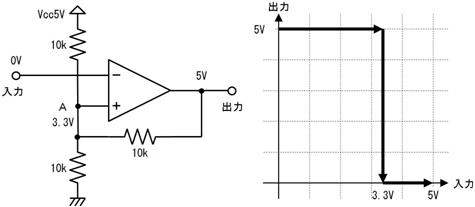
偝偰嵟弶偺忬懺傪丄忋恾偺傛偆偵擖椡偑侽倁偱弌椡偑俆倁偲偟傑偡丅偙偺偲偒丄俙揰偺揹埑偼乽拞揰偺揹埑乿偱寁嶼偟偰丄俁丏俁倁偱偡丅
擖椡揹埑偑師戞偵忋徃偟偰峴偒俁丏俁倁傪墇偊傞偲乮僐儞僷儗乕僞偲摨條偵乯弌椡偑斀揮偟偰侽倁偲側傝傑偡丅乮忋恾塃偺僌儔僼乯
壓恾偼丄斀揮屻偺夞楬偺忬懺偱偡丅弌椡偼侽倁丄俙揰偺揹埑偼侾丏俈倁偱偡丅
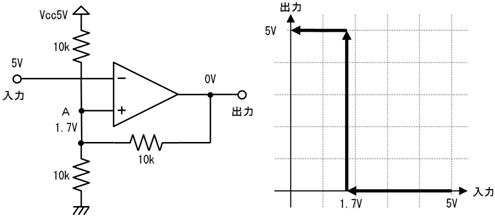
偝偰師偵丄擖椡揹埑偑師戞偵崀壓偟偰峴偒丄侾丏俈倁傪挻偊傞偲丄弌椡偑斀揮偟偰俆倁偲側傝傑偡丅乮忋恾塃偺僌儔僼乯
僔儏儈僢僩僩儕僈偲僐儞僷儗乕僞偺堘偄偼丄僐儞僷儗乕僞偱偼侾偮偟偐側偐偭偨僗儗僢僔儑儖僪揹埑乮鑷抣揹埑乯偑丄僔儏儈僢僩僩儕僈偱偼壓恾偵帵偡傛偆偵俀偮偵憹偊傞偙偲偱偡丅
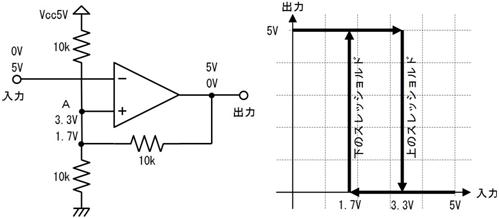
俀偮偺僗儗僢僔儑儖僪傪乽忋偺僗儗僢僔儑儖僪乿乮俁丏俁倁乯丄乽壓偺僗儗僢僔儑儖僪乿乮侾丏俈倁乯偲屇傫偱嬫暿偟傑偡丅
俀侾.侾. 楙廗
壓恾偺僔儏儈僢僩僩儕僈偺忋偺僗儗僢僔儑儖僪偲壓偺僗儗僢僔儑儖僪傪媮傔偰丄擖弌椡揹埑摿惈傪僌儔僼偵婰擖偟偰偔偩偝偄丅扐偟丄僆儁傾儞僾偺亅揹尮抂巕偼傾乕僗偵愙懕偝傟偰偄傞偲偟傑偡丅
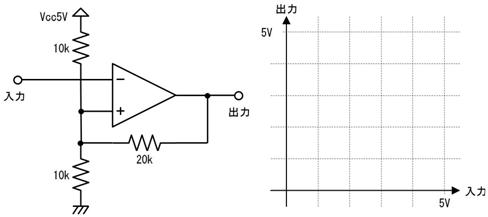
忋偺僗儗僢僔儑儖僪丂丂丂丂倁丂壓偺僗儗僢僔儑儖僪丂丂丂丂倁
俀侾.俀. 摎
偨偲偊偽丄壓恾偺僔乕僩偱拞揰乮俙乯偺揹埑傪寁嶼偡傞丅
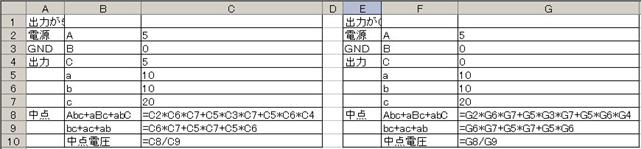
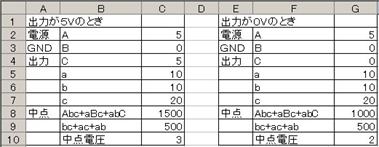
忋恾偺捠傝丄忋偺僗儗僢僔儑儖僪偼俁倁丄壓偺僗儗僢僔儑儖僪偼俀倁偲暘傞丅廬偭偰丄擖弌椡摿惈偼丄壓恾偺捠傝偵側傞丅
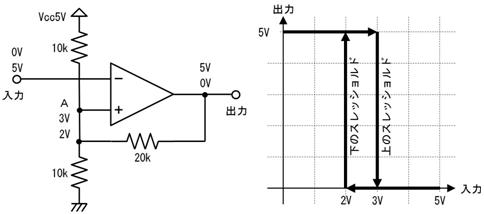
忋偺僗儗僢僔儑儖僪丂丂俁丂倁丂壓偺僗儗僢僔儑儖僪丂丂俀丂倁
俀侾.俁. 楙廗
僗儗僢僔儑儖僪俀丏俆倁偺斀揮僐儞僷儗乕僞偵丄壓恾偵揰慄偱帵偡怣崋傪擖椡偡傞偲丄壓恾偵幚慄偱帵偡怣崋傪弌椡偟傑偟偨丅
忋偺楙廗偱峫偊偨僔儏儈僢僩僩儕僈乮忋偺僗儗僢僔儑儖僪俁倁丄壓偺僗儗僢僔儑儖僪俀倁乯偵丄摨偠怣崋傪擖椡偟偨応崌偺弌椡怣崋傪丄壓恾偵彂偒壛偊偰偔偩偝偄丅傑偨丄僐儞僷儗乕僞偲僔儏儈僢僩僩儕僈偺弌椡怣崋偺堘偄傪愢柧偟偰偔偩偝偄丅
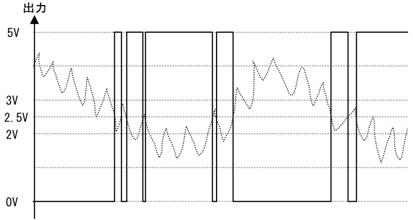
俀侾.係. 摎
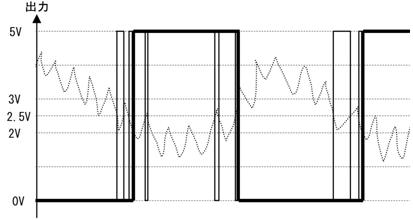
|
弌椡怣崋偺堘偄
僐儞僷儗乕僞偺弌椡偼丄擖椡怣崋偑僗儗僢僔儑儖僪乮俀丏俆倁乯傪墶愗傞偲偒丄弌椡怣崋偑昿斏偵斀揮傪孞傝曉偡丅偟偐偟僔儏儈僢僩僩儕僈偼丄擖椡怣崋偺戝傑偐側忋壓傪斀塮偟偰丄備偭偔傝偲斀揮偡傞丅
|
偙偺傛偆偵丄僔儏儈僢僩僩儕僈偼怳暆偺彫偝側嶨壒偺塭嬁傪梷偊偰丄怣崋偺戝傑偐側曄壔傪懆偊偰斀揮偡傞偙偲偑偱偒傞偨傔丄嶨壒偵傞岆摦嶌傪杊巭偟偨偄応崌偵傕梡偄傜傟傑偡丅
擖椡揹埑偑忋徃偡傞偲弌椡偑亄偵斀揮偟丄擖椡揹埑偑崀壓偡傞偲弌椡偑亅偵斀揮偡傞乮偮傑傝斀揮偟側偄乯僔儏儈僢僩僩儕僈偱偡丅
俀俀.侾. 楙廗
壓恾偑旕斀揮僔儏儈僢僩僩儕僈偺夞楬椺偱偡丅壓昞偵彂偒崬傒側偑傜丄壓恾偺夞楬偺摦嶌傪峫偊丄壓恾偺僌儔僼偵擖弌椡揹埑摿惈傪彂偒崬傫偱偔偩偝偄丅乮偙偙偱偼俆倁扨堦揹尮偱峫偊偰偄傑偡乯
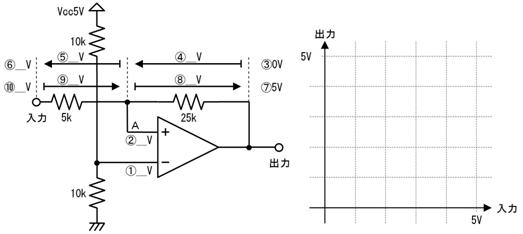
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
侾侽倠兌偱揹尮偺俆倁傪暘埑偟偰偄傞偨傔丄亅擖椡抂巕偺揹埑偼丄
|
倁
|
|
嘇
|
偙偺僆儁傾儞僾偑斀揮偡傞帪偺丄亄擖椡抂巕偺揹埑偺揹埑偼丄
|
倁
|
|
嘋
|
埲壓偱偼丄忋偺嘇偱峫偊偨丄僆儁傾儞僾偑斀揮偡傞弖娫偺奺晹偺揹埑傪峫偊傞丅偮傑傝丄亄擖椡抂巕偑忋偺嘇偱峫偊偨揹埑偲偟偰峫偊傞丅
弌椡偑嘊侽倁偺偲偒丄俀俆倠兌偺椉抂揹埑偼丄
|
倁
|
|
嘍
|
俆倠兌偵偼俀俆倠兌偲摨偠揹棳偑棳傟偰偄傞偐傜丄偦偺椉抂揹埑偼丄
|
倁
|
|
嘐
|
擖椡揹埑偼丄
|
倁
|
|
嘒
|
傑偨丄弌椡偑嘑俆倁偺偲偒丄俀俆倠兌偺椉抂揹埑偼丄
|
倁
|
|
嘓
|
俆倠兌偵偼俀俆倠兌偲摨偠揹棳偑棳傟偰偄傞偐傜丄偦偺椉抂揹埑偼丄
|
倁
|
|
嘔
|
擖椡揹埑偼丄
|
倁
|
|
嘕
|
壓偺僗儗僢僔儑儖僪偼丄
|
倁
|
|
嘖
|
忋偺僗儗僢僔儑儖僪偼丄
|
倁
|
俀俀.俀. 摎
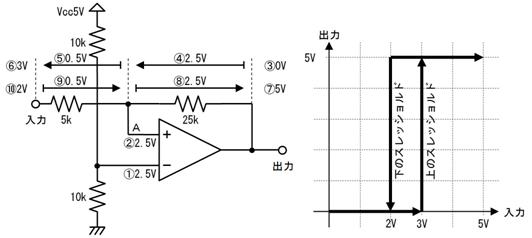
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
侾侽倠兌偱揹尮偺俆倁傪暘埑偟偰偄傞偨傔丄亅擖椡抂巕偺揹埑偼丄
|
俀丏俆倁
|
|
嘇
|
偙偺僆儁傾儞僾偑斀揮偡傞帪偺丄亄擖椡抂巕偺揹埑偺揹埑偼丄
|
俀丏俆倁
|
|
嘋
|
埲壓偱偼丄忋偺嘇偱峫偊偨丄僆儁傾儞僾偑斀揮偡傞弖娫偺奺晹偺揹埑傪峫偊傞丅偮傑傝丄亄擖椡抂巕偑忋偺嘇偱峫偊偨揹埑偲偟偰峫偊傞丅
弌椡偑嘊侽倁偺偲偒丄俀俆倠兌偺椉抂揹埑偼丄
|
俀丏俆倁
|
|
嘍
|
俆倠兌偵偼俀俆倠兌偲摨偠揹棳偑棳傟偰偄傞偐傜丄偦偺椉抂揹埑偼丄
|
侽丏俆倁
|
|
嘐
|
擖椡揹埑偼丄
|
俁倁
|
|
嘒
|
傑偨丄弌椡偑嘑俆倁偺偲偒丄俀俆倠兌偺椉抂揹埑偼丄
|
俀丏俆倁
|
|
嘓
|
俆倠兌偵偼俀俆倠兌偲摨偠揹棳偑棳傟偰偄傞偐傜丄偦偺椉抂揹埑偼丄
|
侽丏俆倁
|
|
嘔
|
擖椡揹埑偼丄
|
俀倁
|
|
嘕
|
壓偺僗儗僢僔儑儖僪偼丄
|
俀倁
|
|
嘖
|
忋偺僗儗僢僔儑儖僪偼丄
|
俁倁
|
俀俁. 柍埨掕儅儖僠僶僀僽儗乕僞
乽柍埨掕乿偲偼暦偒姷傟側偄尵梩偱偡偑丄壓昞偵帵偡乽俀偮偺忬懺偑偁傞夞楬偺庬椶乿偱丄乽柍埨掕乿偵暘椶偝傟傞夞楬丄偮傑傝乽俀偮乮偙偙偱偼丄亄偵怳傝愗偭偨偲偒丄亅偵怳傝愗偭偨偲偒乯偺忬懺偺壗傟偱傕埨掕偣偢丄岎屳偵擖傟懼傢傝傪孞傝曉偡夞楬乿偲偄偆堄枴偱偡丅
俀偮偺忬懺偑偁傞夞楬偺庬椶
|
朚柤
|
塸柤
|
堄枴
|
|
憃埨掕
|
倐倝倱倲倎倐倢倕
僶僀丒僗僥乕僽儖
|
偳偪傜偺忬懺偱傕棷傑傞偙偲偑偱偒傞
|
|
扨埨掕
|
倣倧値倧倱倲倎倐倢倕
儌僲丒僗僥乕僽儖
|
偳偪傜偐堦曽偱偩偗偱棷傑傞偙偲偑偱偒丄懠曽偵愗傝懼偊偰傕丄偟偽傜偔偡傞偲尦偵栠傞
|
|
柍埨掕
|
倎倱倲倎倐倢倕
傾丒僗僥乕僽儖
値倧値倱倲倎倐倢倕
僲儞丒僗僥乕僽儖
|
偳偪傜偺忬懺偵傕棷傑傞偙偲偑偱偒偢丄俀偮偺忬懺傪岎屳偵孞傝曉偡
|
偝偰丄壓恾偼柍埨掕儅儖僠僶僀僽儗乕僞偺夞楬偱偡丅揰慄偱帵偡斀揮僔儏儈僢僩僩儕僈偵丄掞峈偲僐儞僨儞僒偑捛壛偝傟偰偄傑偡丅乮偙偙偱偼俆倁扨堦揹尮偱峫偊偰偄傑偡乯
揰慄晹偼僔儏儈僢僩僩儕僈偲偟偰摦嶌偟傑偡偐傜丄壓恾俛揰乮僔儏儈僢僩僩儕僈偺擖椡乯偺揹埑偑丄忋偺僗儗僢僔儑儖僪乮俁倁乯傪挻偊傟偽弌椡偼侽倁偵斀揮偟丄壓偺僗儗僢僔儑儖僪乮俀倁乯傪壓夞傟偽弌椡偼俆倁偵斀揮偟傑偡丅
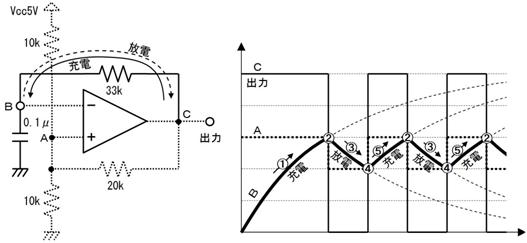
忋恾塃懁偺僌儔僼偼夞楬恾拞偺俙丄俛丄俠揰偺揹埑曄壔傪帵偟傑偡丅偙偺傛偆偵丄夞楬偼師偺嘇嘊嘋嘍乮忋恾塃懁僌儔僼偺斣崋偲懳墳偟偰偄傑偡乯偺摦嶌傪孞傝曉偟偰丄弌椡偑俆倁偺忬懺偲丄弌椡偑侽倁偺忬懺傪岎屳偵孞傝曉偟傑偡丅
嘆乮嵟弶偺堦夞偩偗乯僐儞僨儞僒偼丄嵟弶偺侽倁偐傜弌椡揹埑乮俠揰乯偺俆倁傪栚巜偟偰丄忋恾嵍懁夞楬恾偺幚慄栴報偺宱楬偱廩揹偝傟偰峴偔丅偙偺偨傔俛揰偺揹埑偼師戞偵忋徃偡傞丅
嘇俛揰偺揹埑偑忋偺僗儗僢僔儑儖僪乮俁倁乯傪挻偊傞偲丄弌椡揹埑乮俠揰乯偑侽倁偵斀揮偡傞丅乮俙揰偺揹埑偼俀倁偲側傞乯
嘊僐儞僨儞僒偼丄俁倁偐傜弌椡揹埑乮俠揰乯偺侽倁傪栚巜偟偰丄忋恾嵍懁夞楬恾偺揰慄栴報偺宱楬偱曻揹偝傟偰峴偔丅偙偺偨傔俛揰偺揹埑偼師戞偵崀壓偡傞丅
嘋俛揰偺揹埑偑壓偺僗儗僢僔儑儖僪乮俀倁乯傪壓夞傞偲丄弌椡揹埑乮俠揰乯偑俆倁偵斀揮偡傞丅乮俙揰偺揹埑偼俁倁偲側傞乯
嘍僐儞僨儞僒偼丄俀倁偐傜弌椡揹埑乮俠揰乯偺俆倁傪栚巜偟偰丄忋恾嵍懁夞楬恾偺幚慄栴報偺宱楬偱廩揹偝傟偰峴偔丅偙偺偨傔俛揰偺揹埑偼師戞偵忋徃偡傞丅仺嘇偵栠傝孞傝曉偡
偝偰丄嘇偐傜嘋偵曻揹偡傞偺偵妡偐傞帪娫偼丄乽俠俼夞楬偺曻揹乿偱愢柧偟偨曽朄偱寁嶼偱偒傑偡丅嘇偱偺揹埑偑俁倁乮嵟弶乯丄嘋偱偺揹埑偑俀倁偱偡偐傜丄俤倶們倕倢偱=-0.1E-6*33E3*ln(2/3)偲寁嶼偟偰丄侾丏俁倣昩偲媮傔傞偙偲偑偱偒傑偡丅
崱夞偺夞楬偱偼丄侽倁傪栚巜偟偰曻揹偟偨偨傔偵丄俁倁偲俀倁傪捈愙寁嶼偵巊偆偙偲偑偱偒傑偟偨偑丄偨偲偊偽侽丏俆倁傪栚巜偟偰曻揹偡傞乮幚嵺偺僆儁傾儞僾偱偼椙偔偁傞乯応崌偼丄俀丏俆倁乮俁倁亅侽丏俆倁乯偐傜丄侾丏俆倁乮俀倁亅侽丏俆倁乯傑偱曻揹偡傞丄偲峫偊偰寁嶼偟傑偡丅偮傑傝乽栚巜偡揹埑偲偺嵎乿傪巊偭偰寁嶼偟傑偡丅
偙偺夞楬偱偼丄廩揹偲曻揹偺攇宍偑忋壓懳徧偱丄曻揹帪娫偲廩揹帪娫偑摨偠偱偡偐傜丄敪怳偺廃婜偼俀攞偺俀丏俇倣昩偲側傝丄廃攇悢偼=1/2.6E-3偲寁嶼偟偰丄栺俁俉侽俫倸偱偡丅
幚嵺偵偼丄廩揹偲曻揹偺攇宍偑忋壓懳徾偵側傜側偄応崌偑椙偔偁傝傑偡丅
偙偺夞楬偺摦嶌帪娫偼丄俠亊俼偺抣丄偮傑傝侽丏侾兪偲俁俁倠兌偱寛傑傞帪掕悢冄偵斾椺偟傑偡丅
俀俁.侾. 楙廗
壓恾偺柍埨掕儅儖僠僶僀僽儗乕僞偑曄峏慜偺愝掕偱偼侾俁俀俫倸偱敪怳偟傑偟偨丅偦偺屻丄偙偺夞楬偺掞峈偲僐儞僨儞僒傪壓恾偵帵偡傛偆偵曄峏偟傑偟偨丅曄峏慜偺敪怳廃婜偲丄曄峏屻偺廃婜偲廃攇悢傪丄壓昞偵彂偒崬傒側偑傜媮傔偰偔偩偝偄丅
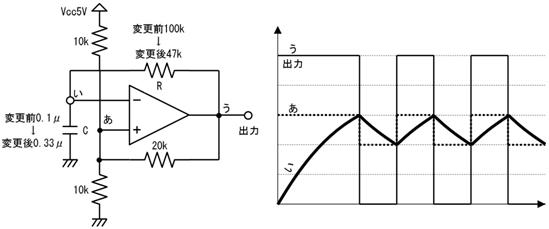
曄峏慜偺廃婜丂丂丂丂倣昩丂曄峏屻偺廃婜丂丂丂丂倣昩丂曄峏屻偺廃攇悢丂丂丂丂俫倸
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
曄峏慜偺廃婜偼丄廃攇悢偺媡悢偩偐傜丄
|
倣昩
|
|
嘇
|
俠偲俼偱摦嶌帪娫偑寛傑傞夞楬偱偼丄
乮摦嶌帪娫傪寛傔偰偄傞俠偲俼埲奜偺愝掕偑摨偠側傜乯
夞楬偺摦嶌帪娫偼丄俠亊俼偺抣乮偮傑傝丄帪掕悢冄乯偵斾椺偟傑偡丅偮傑傝丄
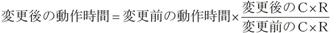
偲寁嶼偱偒傑偡丅
崱夞偺曄峏偱偼丄摦嶌帪娫傪寛傔偰偄傞俠傗俼埲奜偺愝掕乮揹尮揹埑傗摦嶌帪娫傪寛傔偰偄側偄掞峈偺抣乯偼摨偠偱偡偐丄
|
摨偠丒堘偆
|
|
嘋
|
曄峏慜偺俠亊俼偺抣偼丄
|
倣昩
|
|
嘍
|
曄峏屻偺俠亊俼偺抣偼丄
|
倣昩
|
|
嘐
|
曄峏屻偺廃婜偼丄
|
倣昩
|
|
嘑
|
曄峏屻偺廃攇悢偼廃婜偺媡悢偱丄
|
俫倸
|
俀俁.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
曄峏慜偺廃婜偼丄廃攇悢偺媡悢偩偐傜丄
俤倶們倕倢偱=1/132偲寁嶼偟偰丄
|
俈丏俇倣昩
|
|
嘇
|
俠偲俼偱摦嶌帪娫偑寛傑傞夞楬偱偼丄
乮摦嶌帪娫傪寛傔偰偄傞俠偲俼埲奜偺愝掕偑摨偠側傜乯
夞楬偺摦嶌帪娫偼丄俠亊俼偺抣乮偮傑傝丄帪掕悢冄乯偵斾椺偟傑偡丅偮傑傝丄
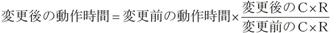
偲寁嶼偱偒傑偡丅
崱夞偺曄峏偱偼丄摦嶌帪娫傪寛傔偰偄傞俠傗俼埲奜偺愝掕乮揹尮揹埑傗摦嶌帪娫傪寛傔偰偄側偄掞峈偺抣乯偼摨偠偱偡偐丄
|
摨偠丒堘偆
|
|
嘋
|
曄峏慜偺俠亊俼偺抣偼丄
=0.1E-6*100E3偲寁嶼偟偰丄
|
侾侽倣昩
|
|
嘍
|
曄峏屻偺俠亊俼偺抣偼丄
=0.33E-6*47E3偲寁嶼偟偰丄
|
侾俇倣昩
|
|
嘐
|
曄峏屻偺廃婜偼丄
=7.6E-3*16/10偲寁嶼偟偰丄
|
侾俀倣昩
|
|
嘑
|
曄峏屻偺廃攇悢偼廃婜偺媡悢偱丄
=1/12E-3偲寁嶼偟偰丄
偁傞偄偼傛傝惓妋偵偼丄慡懱傪捠偠偰丄
=1/(1/132*0.33E-6*47E3/0.1E-6/100E3)偲寁嶼偟偰丄
|
俉俁俫倸
乮俉俆俫倸乯
|
廬偭偰丄
曄峏慜偺廃婜丂俈丏俇倣昩丂曄峏屻偺廃婜丂丂侾俀倣昩丂曄峏屻偺廃攇悢丂丂俉俆俫倸
偲側傝傑偡丅
俀係. 揹棳揹埑曄姺夞楬
壓恾乮倎乯偵帵偡傛偆偵丄僼僅僩僟僀僆乕僪摍偺僙儞僒偼丄椉抂傪抁棈乮僔儑乕僩乯偟偨偲偒偵丄岝偺嫮偝偵斾椺偟偨揹棳偑棳傟傑偡丅偙偺傛偆偵慺巕偺椉抂傪抁棈偟偨忬懺偱丄棳傟傞揹棳傪應掕偱偒傞偺偑丄壓恾乮倐乯偵帵偡揹棳揹埑曄姺夞楬乮僩儔儞僗僐儞僟僋僞儞僗傾儞僾乯偱偡丅
偙偙偱偼僼僅僩僟僀僆乕僪傪懢梲揹抮偺傛偆偵敪揹偝偣傞忬懺偱巊梡偟偰偄傑偡丅乮僼僅僩儃儖僥傿僢僋儌乕僪乛岝揹抧儌乕僪乯偙偺傎偐偵丄僼僅僩僟僀僆乕僪偵媡揹埑乮倁俼乯傪壛偊偰偍偒丄棳傟傞媡揹棳乮俬俼乯傪専弌偡傞乮僼僅僩僐儞僟僋僥傿僽儌乕僪乛岝摫揹儌乕僪乯傕偁傝傑偡丅慜幰偼捈慄惈偑椙岲偱乮俇寘偵傕媦傇捈慄惈乯丄屻幰偼墳摎懍搙偑崅偔側傝傑偡丅
俀係.侾. 楙廗
忋恾乮倐乯傪嶲峫偵壓昞偵婰擖偟側偑傜丄揹棳揹埑曄姺夞楬偺摦嶌傪専摙偟偰偔偩偝偄丅
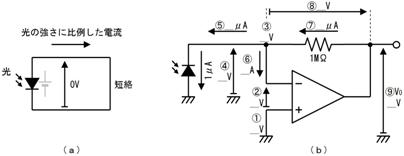
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄
乮傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
倁
|
|
嘇
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
乮侾俵兌偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
倁
|
|
嘊
|
亅擖椡偺揹埑偼丄
|
倁
|
|
嘋
|
僟僀僆乕僪偺椉抂揹埑偼丄
|
倁
|
|
|
嘋偐傜丄僟僀僆乕僪偼抁棈偟偨忬懺偲側傞偙偲偑暘偐傝傑偡丅
|
|
|
嘍
|
擖椡晹傪嵍偵岦偐偭偰棳傟傞揹棳偼丄
乮僟僀僆乕僪偺岝揹棳偑侾兪俙偩偐傜丄乯
|
兪俙
|
|
嘐
|
亅擖椡偵棳傟傞揹棳偼丄
|
俙
|
|
嘑
|
婣娨掞峈乮侾俵兌乯偵棳傟傞揹棳偼丄
乮嘍嘐偲僉儖僸懃偐傜丄乯
|
兪俙
|
|
嘒
|
婣娨掞峈偺椉抂揹埑偼丄
乮僆乕儉懃傛傝丄乯
|
倁
|
|
嘓
|
弌椡揹埑偼丄
|
倁
|
俀係.俀. 摎
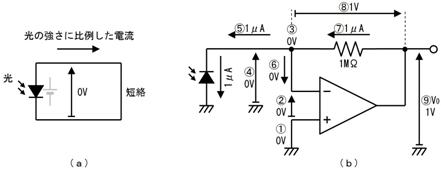
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄
乮傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
侽倁
|
|
嘇
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
乮侾俵兌偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
侽倁
|
|
嘊
|
亅擖椡偺揹埑偼丄
|
侽倁
|
|
嘋
|
僟僀僆乕僪偺椉抂揹埑偼丄
|
侽倁
|
|
|
嘋偐傜丄僟僀僆乕僪偼抁棈偟偨忬懺偲側傞偙偲偑暘偐傝傑偡丅
|
|
|
嘍
|
擖椡晹傪嵍偵岦偐偭偰棳傟傞揹棳偼丄
乮僟僀僆乕僪偺岝揹棳偑侾兪俙偩偐傜丄乯
|
侾兪俙
|
|
嘐
|
亅擖椡偵棳傟傞揹棳偼丄
|
侽俙
|
|
嘑
|
婣娨掞峈乮侾俵兌乯偵棳傟傞揹棳偼丄
乮嘍嘐偲僉儖僸懃偐傜丄乯
|
侾兪俙
|
|
嘒
|
婣娨掞峈偺椉抂揹埑偼丄
乮僆乕儉懃傛傝丄乯
|
侾倁
|
|
嘓
|
弌椡揹埑偼丄
|
侾倁
|
偙偺傛偆偵丄揹棳揹埑曄姺夞楬傪巊梡偡傞偙偲偱丄僟僀僆乕僪偺椉抂傪抁棈偟偨乮侽倁偵偟偨乯忬懺偱丄僟僀僆乕僪偵棳傟偨揹棳偵斾椺偟偨揹埑傪弌椡偡傞偙偲偑偱偒傑偡丅
嬌庛偄岝傪應掕偡傞応崌偼丄壓恾偵帵偡傛偆偵丄夞楬慡懱傪僔乕儖僪働乕僗偵擖傟偰丄應掕岝傪働乕僗偵愝偗偨嬥栐摍偐傜僟僀僆乕僪偵徠幩偟傑偡丅
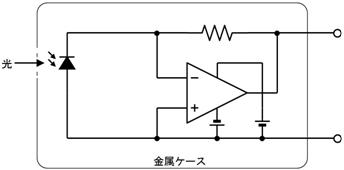
忋恾偺傛偆偵丄揹尮偵揹抮傪梡偄偰僔乕儖僪働乕僗偺拞偵擖傟傞偲丄揹尮偵婲場偡傞僲僀僘傕杊偖偙偲偑偱偒傑偡丅
壓恾偺夞楬偼丄擖椡偑僾儔僗偺応崌偼斀揮偟偰弌椡偝傟傑偡偑丄擖椡偑儅僀僫僗偺応崌偼弌椡偼侽倁偺傑傑偱曄壔偟傑偣傫丅偙偺傛偆側夞楬傪敿攇惍棳夞楬偲屇傃傑偡丅
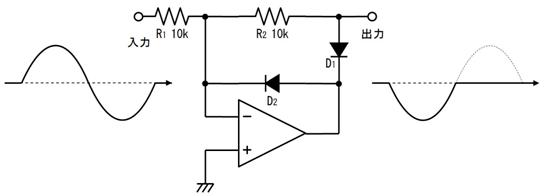
俀俆.侾. 楙廗
忋恾偺敿攇惍棳夞楬偵亄侾侽倁傪壛偊偨応崌偺奺晹偺揹埑乛揹棳傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
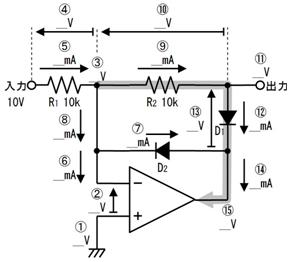
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄
乮傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
倁
|
|
嘇
|
亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮掞峈傗僟僀僆乕僪偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
倁
|
|
嘊
|
亄擖椡偺揹埑偼丄
|
倁
|
|
嘋
|
俼侾偺椉抂揹埑偼丄
|
倁
|
|
嘍
|
俼侾偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘐
|
僆儁傾儞僾偺擖椡偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘑
|
俢俀傪塃岦偒偵棳傟傞揹棳偼丄
乮媡曽岦偩偐傜丄乯
|
倣俙
|
|
嘒
|
俼侾偺塃懁偐傜亅擖椡偵岦偐偭偰棳傟傞揹棳偼丄
乮嘑丄嘐偐傜丄乯
|
倣俙
|
|
嘓
|
俼俀偵棳傟傞揹棳偼丄
乮嘍丄嘒偐傜丄乯
|
倣俙
|
|
嘔
|
俼俀偺椉抂揹埑偼丄
|
倁
|
|
嘕
|
弌椡揹埑偼丄
|
倁
|
|
嘖
|
俢侾偵棳傟傞揹棳偼丄
乮嘓偐傜丄乯
|
倣俙
|
|
嘗
|
俢侾偺椉抂揹埑偼丄
|
倁
|
|
嘙
|
僆儁傾儞僾偺弌椡抂巕偵棳傟崬傓揹棳偼丄
|
倣俙
|
俀俆.俀. 摎
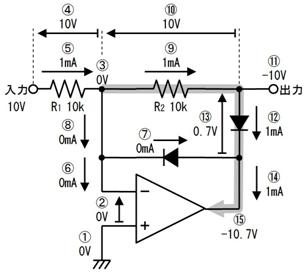
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄
乮傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
侽倁
|
|
嘇
|
亄擖椡偲亅擖椡偺揹埑嵎偼丄
乮掞峈傗僟僀僆乕僪偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
侽倁
|
|
嘊
|
亄擖椡偺揹埑偼丄
|
侽倁
|
|
嘋
|
俼侾偺椉抂揹埑偼丄
|
侾侽倁
|
|
嘍
|
俼侾偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘐
|
僆儁傾儞僾偺擖椡偵棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘑
|
俢俀傪塃岦偒偵棳傟傞揹棳偼丄
乮媡曽岦偩偐傜丄乯
|
侽倣俙
|
|
嘒
|
俼侾偺塃懁偐傜亅擖椡偵岦偐偭偰棳傟傞揹棳偼丄
乮嘑丄嘐偐傜丄乯
|
侽倣俙
|
|
嘓
|
俼俀偵棳傟傞揹棳偼丄
乮嘍丄嘒偐傜丄乯
|
侾倣俙
|
|
嘔
|
俼俀偺椉抂揹埑偼丄
|
侾侽倁
|
|
嘕
|
弌椡揹埑偼丄
|
亅侾侽倁
|
|
嘖
|
俢侾偵棳傟傞揹棳偼丄
乮嘓偐傜丄乯
|
侾倣俙
|
|
嘗
|
俢侾偺椉抂揹埑偼丄
|
侽丏俈倁
|
|
嘙
|
僆儁傾儞僾偺弌椡抂巕偵棳傟崬傓揹棳偼丄
|
侾倣俙
|
偙偺傛偆偵擖椡揹埑偑僾儔僗偺偲偒偼丄擖椡揹埑偑斀揮偟偰弌椡偵尰傟傑偡丅
俀俆.俁. 楙廗
忋恾偺敿攇惍棳夞楬偵亅侾侽倁傪壛偊偨応崌偺奺晹偺揹埑乛揹棳傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
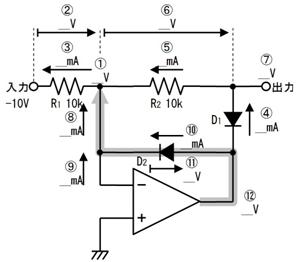
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亅擖椡偺揹埑偼丄
|
倁
|
|
嘇
|
俼侾偺椉抂揹埑偼丄
|
倁
|
|
嘊
|
俼侾偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘋
|
俢侾傪忋岦偒偵棳傟傞揹棳偼丄
乮媡曽岦偩偐傜丄乯
|
倣俙
|
|
嘍
|
俼俀傪棳傟傞揹棳偼丄
|
倣俙
|
|
嘐
|
俼俀偺椉抂揹埑偼丄
|
倁
|
|
嘑
|
弌椡揹埑偼丄
|
倁
|
|
嘒
|
俼侾偺塃懁偵岦偐偭偰搊傞揹棳偼丄
|
倣俙
|
|
嘓
|
亅擖椡偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘔
|
俢俀傪嵍岦偒偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘕
|
俢俀偺椉抂揹埑偼丄
|
倁
|
|
嘖
|
僆儁傾儞僾偺弌椡抂巕偺揹埑偼丄
|
倁
|
俀俆.係. 摎
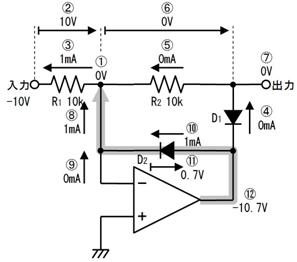
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亅擖椡偺揹埑偼丄
|
侽倁
|
|
嘇
|
俼侾偺椉抂揹埑偼丄
|
侾侽倁
|
|
嘊
|
俼侾偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘋
|
俢侾傪忋岦偒偵棳傟傞揹棳偼丄
乮媡曽岦偩偐傜丄乯
|
侽倣俙
|
|
嘍
|
俼俀傪棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘐
|
俼俀偺椉抂揹埑偼丄
|
侽倁
|
|
嘑
|
弌椡揹埑偼丄
|
侽倁
|
|
嘒
|
俼侾偺塃懁偵岦偐偭偰搊傞揹棳偼丄
|
侾倣俙
|
|
嘓
|
亅擖椡偵棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘔
|
俢俀傪嵍岦偒偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘕
|
俢俀偺椉抂揹埑偼丄
|
侽丏俈倁
|
|
嘖
|
僆儁傾儞僾偺弌椡抂巕偺揹埑偼丄
|
亅侾侽丏俈倁
|
偙偺傛偆偵擖椡揹埑偑儅僀僫僗偺応崌偼丄弌椡揹埑偼侽倁偱曄壔偟傑偣傫丅壓恾偺傛偆偵僟僀僆乕僪偺岦偒傪媡偵偡傞偲偙偱丄擖椡偑儅僀僫僗偺応崌偵弌椡偑弌傞夞楬偵曄峏偱偒傑偡丅
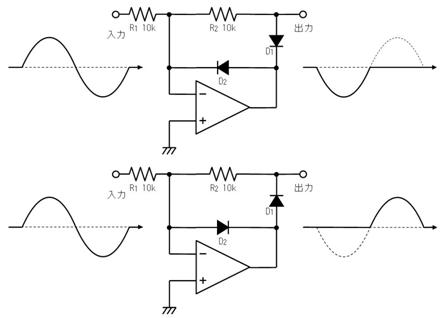
壓恾偺傛偆偵敿攇惍棳夞楬偺弌椡乮傠乯偲丄擖椡怣崋乮偄乯傪俀丗侾偺妱崌偱壛偊傞偲丄慡攇惍棳攇宍乮偼乯傪弌椡偱偒傑偡丅
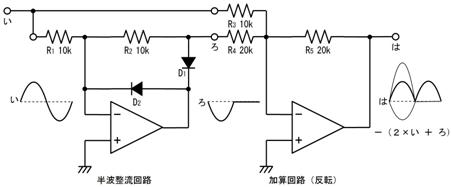
忋恾偺夞楬偼丄僾儔僗偺揹埑偑擖椡偝傟偰傕丄儅僀僫僗偺揹埑偑擖椡偝傟偰傕丄僾儔僗偺揹埑偑弌椡偝傟傞偺偱丄愨懳抣夞楬偲屇偽傟傑偡丅
壓恾偺傛偆偵僐儞僨儞僒俠侾傪捛壛偡傞偲丄弌椡攇宍傪側傔傜偐偵偟偰乮暯妸偟偰乯丄暯嬒揹埑傪弌椡偡傞偙偲偑偱偒傑偡丅
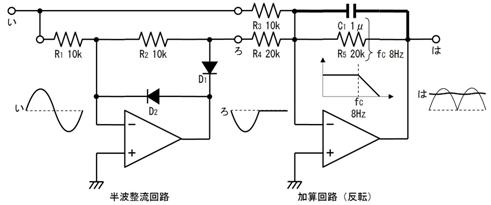
忋恾偺夞楬偺暯妸偺帪掕悢偼=C1*R5偱丄僇僢僩僆僼廃攇悢偼=1/2/pi()/C1/R5偱寁嶼偱偒傑偡丅僇僢僩僆僼廃攇悢偑丄怣崋廃攇悢偺侾侽侽暘偺侾掱搙偱偁傟偽丄怣崋惉暘傪杦偳娷傑側偄妸傜偐側暯嬒揹埑偑弌椡偝傟傑偡丅
壓恾偼嵟戝抣専攇夞楬偱偡丅亄擖椡偵侾倁傪壛偊傞偲丄亅擖椡揹埑偑侾倁偵側傞傑偱僟僀僆乕僪傪捠偠偰僐儞僨儞僒偑廩揹偝傟傑偡乮壓恾幚慄栴報偺宱楬乯丅偦偺屻亄擖椡揹埑偑壓偑偭偰傕僟僀僆乕僪偑媡揹埑偵側傞偨傔僆儁傾儞僾偼僐儞僨儞僒傪曻揹偡傞偙偲偑偱偒傑偣傫丅曻揹偼掞峈傪捠偠偰備偭偔傝偲峴傢傟傑偡乮壓恾揰慄栴報偺宱楬乯丅
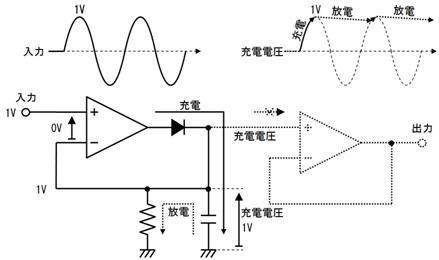
偦偺寢壥丄僐儞僨儞僒偼擖椡揹埑偺嵟戝抣偵懍傗偐偵廩揹偝傟丄備偭偔傝偲曻揹偝傟傑偡丅僐儞僨儞僒偺揹埑偵塭嬁傪梌偊側偄傛偆偵丄忋恾偵揰慄偱帵偡乽儐僯僥傿僎僀儞憹暆婍乿傪愝偗偰丄弌椡傪庢傝弌偟傑偡丅
偙傟傑偱丄僆儁傾儞僾偑乽棟憐揑側惈擻乿傪帩偭偰偄傞偲峫偊偰乮棟憐僆儁傾儞僾偲峫偊偰乯夞楬偺摥偒傪愢柧偟偰棃傑偟偨丅
婛偵弎傋偨傛偆偵丄僆儁傾儞僾偺惈擻偼偐側傝岦忋偟偰偄傑偡偐傜丄夞楬偺庬椶傗僆儁傾儞僾偺昳庬偵傛偭偰偼乽棟憐揑側惈擻乿偲峫偊偰傕栤戣側偄応崌傕憹偊偰偄傑偡丅偟偐偟丄棟憐揑偲偼尵偊側偄晹暘傪棟夝偡傞偙偲偱丄摨偠僆儁傾儞僾偱傕丄傛傝崅偄惈擻偑堷偒弌偣偨傝丄傛傝埨壙側僆儁傾儞僾偱嵪傑偡偙偲偑偱偒傞傛偆偵側傝傑偡丅
偙偙偱偼丄僆儁傾儞僾偺乽棟憐揑偱側偄乿晹暘傪愢柧偟乮棟憐揑偱偼側偄偨傔偵乯夞楬偺摦嶌偵偳偺傛偆側塭嬁偑弌傞偺偐峫偊丄昁梫偑偁傟偽懳嶔偺曽朄傪夝愢偟傑偡丅
壓恾偺俁夞楬偼偄偢傟傕侾侽攞偺旕斀揮憹暆夞楬偱偡偑丄掞峈偺抣偑偦傟偧傟堎側傝傑偡丅棟憐僆儁傾儞僾偱偁傟偽丄偳偺夞楬傕惓偟偔摦嶌偡傞敜偱偡丅
巊梡偡傞掞峈抣偑崅偄掱丄棳傟傞揹棳偑尭傝丄敪擬傗徚旓揹椡偑彮側偔側傝傑偡偐傜丄壗偺栤戣傕柍偗傟偽丄掞峈抣偺嵟傕崅偄乮倎乯偺夞楬傪巊偄偨偄偲偙傠偱偡丅
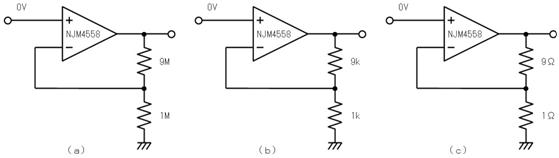
偙偺夞楬偱偼僆儁傾儞僾偺乽棟憐揑偱側偄乿晹暘偺拞偱乽擖椡僶僀傾僗揹棳乿偑栤戣偵側傝傑偡丅
僆儁傾儞僾偺廳梫側惈幙嘋偵乽擖椡抂巕偵偼揹棳偑棳傟側偄乿偑偁傝傑偟偨丅偲偙傠偑幚嵺偵偼嬐偐側揹棳偑擖椡抂巕偵棳傟傑偡丅偙偺揹棳偑擖椡僶僀傾僗揹棳偱偡丅捠忢丄擖椡僶僀傾僗揹棳偼丄擖椡揹埑偵娭學側偔忢偵堦掕偺戝偒偝偱棳傟傑偡丅
壓昞偵俶俰俵係俆俆俉偺僨乕僞僔乕僩偺堦晹傪帵偟傑偡丅昞偺俁峴栚偵乽擖椡僶僀傾僗揹棳乿偺抣偑婰嵹偝傟偰偄傑偡丅
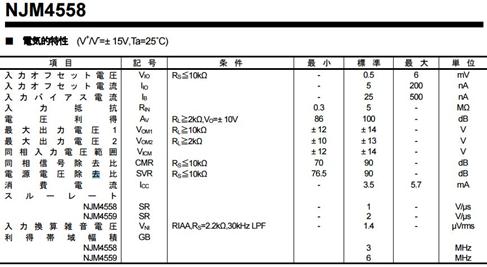
俶俰俵係俆俆俉偺擖椡僶僀傾僗揹棳偼俀俆乣俆侽侽値俙偱偡丅扨埵偑乽値俙乿偱偡偐傜丄妋偐偵旕忢偵彫偝側揹棳偱偡偑丄偙傟偱傕夞楬偵傛偭偰偼塭嬁偑偁傝傑偡丅
俶俰俵係俆俆俉偺埵抲晅偗
偙偙偱偼乽棟憐僆儁傾儞僾偲尰幚偺僆儁傾儞僾偺堘偄乿傪嫮挷偡傞偨傔偵俶俰俵係俆俆俉傪庢傝忋偘傑偡丅偮傑傝係俆俆俉偼丄僆僼僙僢僩傗僶僀傾僗揹棳偑懡偔丄弌椡僗僀儞僌偑彫偝偔丄崅偄廃攇悢偼憹暆偱偒側偄摍偲丄棟憐僆儁傾儞僾偐傜偼掱墦偄惈擻偱偡丅惈擻偼僀儅僀僠偱偡偑丄埨壙偱偁傝丄傑偨丄惈幙傪妶偐偟偨巊偄曽偑妋棫偟偰偄傞偨傔丄塱傜偔棙梡偝傟傑偟偨丅揹尮揹埑偑掅偄偲巊偄擄偄偺偱丄崱屻偼搼懣偝傟偰峴偔偱偟傚偆丅
僆儁傾儞僾偼侾俋俇侽擭戙拞偛傠偐傜兪俙俈侽俀丄俈侽俋偲恑曕偟丄俇俉擭偺俈係侾偱旕忢偵巊偄傗偡偔側傝傑偟偨丅俼俠係俆俆俉偼丄侾俋俈侽擭戙偵儗僀僙僆儞幮偑俈係侾傪夵椙偟偰乮弶抜傪俹俶俹偵曄峏乯掅嶨壒壔偟偨偟偨僆儁傾儞僾偱丄俶俰俵係俆俆俉偼偦偺僙僇儞僪僜乕僗乮偦偭偔傝偝傫乯偱偡丅掅嶨壒偺摿惈傪妶偐偟偰僆乕僨傿僆婡婍偵懡梡偝傟傑偟偨丅
侾.侾. 楙廗乮擖椡僶僀傾僗揹棳偺塭嬁乯
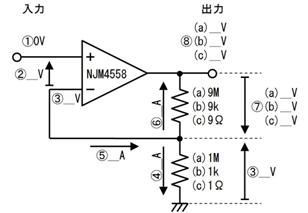
偱偼丄忋恾傪尒側偑傜壓昞偵婰擖偟偰丄嵟弶偺俁偮偺夞楬偱擖椡僶僀傾僗揹棳傪塭嬁傪峫偊傑偡丅
|
|
幙栤
|
摎
|
|
嘆
|
擖椡揹埑偼
|
侽倁丂丂
|
|
嘇
|
晧婣娨偺夞楬偩偐傜亄擖椡偲亅擖椡偺娫偺揹埑偼丄
|
倁
|
|
嘊
|
亅擖椡抂巕偺揹埑偼丄
|
倁
|
|
嘋
|
壓懁偺掞峈偵棳傟傞揹棳偼丄
|
俙
|
|
嘍
|
俶倀俵係俆俆俉偺擖椡僶僀傾僗揹棳乮嵟戝抣乯偼丄
|
俙
|
|
嘐
|
忋懁偺掞峈偵棳傟傞揹棳偼丄
|
俙
|
|
嘑
|
忋懁偺掞峈偵敪惗偡傞揹埑偼丄
|
乮倎乯偺応崌
|
乮倐乯偺応崌
|
乮們乯偺応崌
|
|
倁
|
倁
|
倁
|
|
嘒
|
弌椡揹埑偼丄
|
倁
|
倁
|
倁
|
侾.俀. 摎
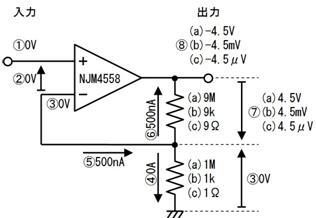
|
|
幙栤
|
摎
|
|
嘆
|
擖椡揹埑偼
|
侽倁
|
|
嘇
|
晧婣娨偺夞楬偩偐傜亄擖椡偲亅擖椡偺娫偺揹埑偼丄
|
侽倁
|
|
嘊
|
亅擖椡抂巕偺揹埑偼丄
|
侽倁
|
|
嘋
|
壓懁偺掞峈偵棳傟傞揹棳偼丄
|
侽俙
|
|
嘍
|
俶倀俵係俆俆俉偺擖椡僶僀傾僗揹棳乮嵟戝抣乯偼丄
|
俆侽侽値俙
|
|
嘐
|
忋懁偺掞峈偵棳傟傞揹棳偼丄
|
俆侽侽値俙
|
|
嘑
|
忋懁偺掞峈偵敪惗偡傞揹埑偼丄
|
乮倎乯偺応崌
|
乮倐乯偺応崌
|
乮們乯偺応崌
|
|
係丏俆倁
|
係丏俆倣倁
|
係丏俆兪倁
|
|
嘒
|
弌椡揹埑偼丄
|
亅係丏俆倁
|
亅係丏俆倣倁
|
亅係丏俆兪倁
|
偮傑傝丄杮棃偱偁傟偽擖椡偺侽倁偺侾侽攞丄偮傑傝侽倁偑弌椡偝傟傞敜偱偡偑丄椺偊偽乮倎乯偱偼亅係丏俆倁偑弌椡偝傟偰偄傑偡丅偙傟偼巊偊偦偆偵偁傝傑偣傫丅
乮倐乯偱偁傟偽丄亅係丏俆倣倁偲偐側傝彫偝偔側傝丄乮們乯偱偼亅係丏俆兪倁偲應掕偑擄偟偄傎偳彫偝偔側偭偰偄傑偡丅偱偡偐傜丄擖椡僶僀傾僗揹棳偺塭嬁傪旔偗傞偨傔偵偼乮倐乯偐乮們乯傪慖傇傋偒偱偡丅
侾.俁. 楙廗乮夞楬揹棳乯
偙偺傛偆側擖椡僶僀傾僗揹棳偺専摙偲暯峴偟偰丄夞楬偵棳偡揹棳傕専摙偟傑偡丅係俆俆俉摍偺斈梡僆儁傾儞僾傪巊偭偨夞楬偼丄庡偵嵟戝侾乣侾侽倣俙掱搙偺揹棳偱摦嶌偝偣傑偡丅乮僆儁傾儞僾偺昳庬偵傛偭偰偼丄侾侽乣侾侽侽兪俙偱摦嶌偝偣傞帠傕壜擻偱偡乯
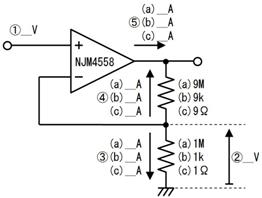
忋恾傪尒側偑傜壓昞偵彂偒崬傒丄擖椡偵侾倁傪壛偊偨応崌偺丄夞楬偵棳傟傞揹棳傪専摙偟偰偔偩偝偄丅乮擖椡僶僀傾僗揹棳偺塭嬁偼柍帇偟偰専摙偟偰偔偩偝偄乯
|
|
幙栤
|
乮倎乯偺応崌
|
乮倐乯偺応崌
|
乮們乯偺応崌
|
|
嘆
|
擖椡揹埑偼丄
|
倁
|
倁
|
倁
|
|
嘇
|
壓懁偺掞峈偺揹埑偼丄
|
倁
|
倁
|
倁
|
|
嘊
|
壓懁偺掞峈偺揹棳偼丄
|
俙
|
俙
|
俙
|
|
嘋
|
忋懁偺掞峈偺揹棳偼丄
|
俙
|
俙
|
俙
|
|
嘍
|
僆儁傾儞僾偑弌椡偡傞揹棳偼丄
|
俙
|
俙
|
俙
|
侾.係. 摎
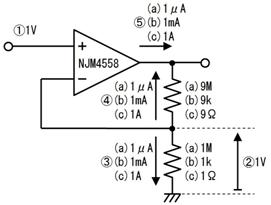
|
|
幙栤
|
乮倎乯偺応崌
|
乮倐乯偺応崌
|
乮們乯偺応崌
|
|
嘆
|
擖椡揹埑偼丄
|
侾倁
|
侾倁
|
侾倁
|
|
嘇
|
壓懁偺掞峈偺揹埑偼丄
|
侾倁
|
侾倁
|
侾倁
|
|
嘊
|
壓懁偺掞峈偺揹棳偼丄
|
侾兪俙
|
侾倣俙
|
侾俙
|
|
嘋
|
忋懁偺掞峈偺揹棳偼丄
|
侾兪俙
|
侾倣俙
|
侾俙
|
|
嘍
|
僆儁傾儞僾偑弌椡偡傞揹棳偼丄
|
侾兪俙
|
侾倣俙
|
侾俙
|
乮倎乯偺夞楬偼掞峈抣偑崅偄偨傔丄嬐偐側乮侾兪俙乯側揹棳偟偐棳傟偰偄傑偣傫丅徣揹椡偺実懷婡婍偱偼丄擖椡僶僀傾僗揹棳偺彫偝側僆儁傾儞僾傪巊梡偟偰丄偙偺掱搙偺揹棳偱摦嶌偝偣傞偙偲傕椙偔偁傝傑偡丅乮傕偪傠傫丄俶俰俵係俆俆俉偱偼柍棟偱偡乯
乮們乯偺夞楬偼掞峈抣偑偲偰傕彫偝偔丄椺偊偽侾倁傪擖椡偟偨偲偒偵僆儁傾儞僾偼侾俙傪偺揹棳傪弌椡偡傞昁梫偑偁傝傑偡丅偟偐偟丄係俆俆俉偑弌椡偱偒傞偺偼丄偨偐偩偐侾侽乣俀侽倣俙偱偡偐傜丄侾俙偼偲偰傕柍棟偱偡丅揹尮揹棳傕侾俙埲忋徚旓偡傞偙偲偵側傝丄敪擬傕戝偒偔側傝傑偡丅
偦偙偱乮倐乯偺夞楬偱偁傟偽丄夞楬揹棳偼侾倣俙偲丄俶倀俵係俆俆俉偑弌椡偱偒傞戝偒偝偵廂傑偭偰偄傑偡丅
偙偺傛偆偵夞楬揹棳偼丄壓昞偵帵偡偲偍傝丄乮侾乯擖椡僶僀傾僗揹棳偵斾傋傟偽廫暘戝偒偔丄乮俀乯僆儁傾儞僾偺弌椡揹棳傛傝偼彫偝偄斖埻偵愝掕偟傑偡丅
|
僆儁傾儞僾偺巇條
俶俰俵係俆俆俉偺椺
|
戝彫娭學
|
夞楬揹棳
|
|
擖椡僶僀傾僗揹棳
乮嵟戝俆侽侽値俙乯
|
亙亙
|
擖椡僶僀傾僗揹棳傛傝廫暘戝偒偔偡傞
|
|
惛搙偺媮傔傜傟側偄夞楬偱傕丄擖椡僶僀傾僗揹棳偺嵟掅侾侽侽攞埲忋
乮俆侽兪俙埲忋乯
|
|
惛搙偺媮傔傜傟傞夞楬偱偼侾侽侽侽攞偐偦傟埲忋
乮侽丏俆倣俙埲忋乯
|
|
僆儁傾儞僾偺嵟戝弌椡揹棳
乮侾侽倣俙乯
嫋梕偱偒傞揹尮偺徚旓揹棳傛傝彫偝偔偡傞
|
亜
|
敪擬偑尷搙撪偱偁傟偽丄偓傝偓傝傑偱巊梡偱偒傞
乮侾侽倣俙埲壓乯
|
侾.俆. 擖椡僶僀傾僗揹棳傪懪偪徚偡夞楬
夞楬偵傛偭偰偼丄偨偲偊擖椡僶僀傾僗揹棳偑棳傟偰傕丄偦偺塭嬁偑憡嶦偟偰塭嬁傪彫偝偔偡傞偙偲偑偱偒傑偡丅壓恾偼僶僀傾僗揹棳偺塭嬁傪憡嶦偟偨岎棳斀揮憹暆夞楬偺椺偱偡丅
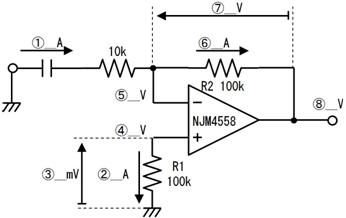
忋恾傪尒側偑傜丄壓昞偵婰擖偟偰擖椡僶僀傾僗揹棳偺塭嬁偑憡嶦偝傟傞條巕傪専摙偟傑偡丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡僐儞僨儞僒傪捠偟偰棳傟崬傫偱偔傞捈棳揹棳偼丄
|
俙
|
|
嘇
|
俶俰俵係俆俆俉偺嵟戝擖椡僶僀傾僗揹棳偼丄
|
値俙
|
|
嘊
|
擖椡僶僀傾僗揹棳偵傛偭偰俼侾偵敪惗偡傞揹埑偼丄
|
倣倁
|
|
嘋
|
亄擖椡抂巕偺揹埑偼丄
|
倣倁
|
|
嘍
|
晧婣娨偑妡偐偭偰偄傞偐傜丄亅擖椡抂巕偺揹埑偼丄
|
倣倁
|
|
嘐
|
俼俀偵棳傟傞嵟戝擖椡僶僀傾僗揹棳偼丄
|
値俙
|
|
嘑
|
擖椡僶僀傾僗揹棳偵傛偭偰俼俀偵敪惗偡傞揹埑偼丄
|
倣倁
|
|
嘒
|
弌椡揹埑偼丄
|
倁
|
侾.俇. 摎
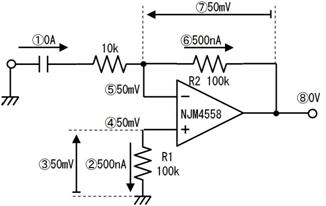
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡僐儞僨儞僒傪捠偟偰棳傟崬傫偱偔傞捈棳揹棳偼丄
|
侽俙
|
|
嘇
|
俶俰俵係俆俆俉偺嵟戝擖椡僶僀傾僗揹棳偼丄
|
俆侽侽値俙
|
|
嘊
|
擖椡僶僀傾僗揹棳偵傛偭偰俼侾偵敪惗偡傞揹埑偼丄
|
俆侽倣倁
|
|
嘋
|
亄擖椡抂巕偺揹埑偼丄
|
俆侽倣倁
|
|
嘍
|
晧婣娨偑妡偐偭偰偄傞偐傜丄亅擖椡抂巕偺揹埑偼丄
|
俆侽倣倁
|
|
嘐
|
俼俀偵棳傟傞嵟戝擖椡僶僀傾僗揹棳偼丄
|
俆侽侽値俙
|
|
嘑
|
擖椡僶僀傾僗揹棳偵傛偭偰俼俀偵敪惗偡傞揹埑偼丄
|
俆侽倣倁
|
|
嘒
|
弌椡揹埑偼丄
|
侽倁
|
擖椡僶僀傾僗揹棳偼摨偠昳庬偱傕屄懱枅偵堎側傝傑偡偟丄壏搙偱傕曄壔偟傑偡丅偟偐偟丄亄擖椡偲亅擖椡偺僶僀傾僗揹棳偼傎傏摨偠偱偁傞偨傔丄忋恾偺夞楬偱塭嬁傪懪偪徚偡偙偲偑偱偒傑偡丅
婣娨掞峈乮忋恾偺俼俀乯偺抣偑戝偒偔丄擖椡僶僀傾僗揹棳偑俼俀偵棳傟偰敪惗偡傞揹埑偑丄惓忢側夞楬偺摦嶌乮偳偙傑偱偑惓忢偐偼丄夞楬偺梡搑偱寛傑傝傑偡乯傪嫸傢偣傞応崌偼丄忋恾俼侾偺傛偆側懳嶔傪巤偟傑偡丅偨偩偟丄俠俵俷俽僆儁傾儞僾偺傛偆側擖椡僶僀傾僗揹棳偺彫偝側僆儁傾儞僾偱偼丄俼侾偼晄梫偱偡丅
旕斀揮憹暆夞楬偺応崌傕丄壓恾偺傛偆偵擖椡僶僀傾僗揹棳偱敪惗偡傞揹埑傪亄擖椡偲亅擖椡偱摍偟偔偡傞偙偲偱丄塭嬁傪憡嶦偱偒傑偡丅
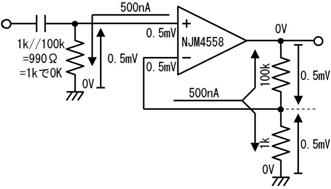
俠俵俷俽僆儁傾儞僾偱偼丄擖椡僶僀傾僗揹棳偼乽杮摉偵柍偄乿偲尵偊傞掱彫偝偔側傝丄崅偄掞峈抣偺夞楬傪巊梡偟偰傕乮僶僀傾僗揹棳偺乯塭嬁偑弌側偔側傝傑偡丅
壓昞偵俠俵俷俽僆儁傾儞僾丄俶俰俵俈侽係係偺僨乕僞僔乕僩偺堦晹傪帵偟傑偡丅昞偺俁峴栚偵乽擖椡僶僀傾僗揹棳乿偺抣偑婰嵹偝傟偰偄傑偡丅
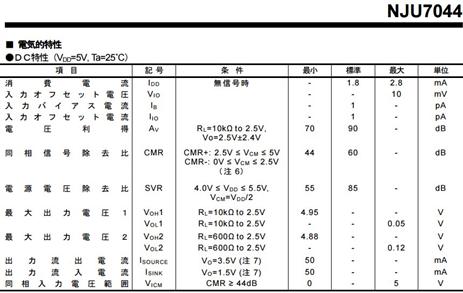
擖椡僶僀傾僗揹棳偼侾倫俙偲旕忢偵彫偝偔側偭偰偄傑偡丅侾倫俙偱偁傟偽丄侾侽俵兌偺掞峈偵棳傟偰傕丄侾侽兪倁偺揹埑偟偐惗偠傑偣傫丅擖椡僶僀傾僗揹棳偺塭嬁傪乽柍偄乿偲峫偊偰愝寁偱偒傑偡丅乮偝傜偵俴俵俠俇俇侽偱偼俁倖俙傑偱彫偝偔側偭偰偄傑偡乯
扐偟崅掞峈偺夞楬偼丄暿搑愢柧偡傞乽擬嶨壒乿傗乽僗僩儗僀梕検乿偺塭嬁偵傛傝丄嶨壒偑憹偊丄崅偄廃攇悢偑憹暆偱偒側偔側傞偨傔丄夞楬偺栚揑傪峫偊偰丄栤戣偺柍偄斖埻偱崅掞峈傪巊梡偟傑偡丅
俁. 嵟戝弌椡揹棳
擖椡僶僀傾僗揹棳偺崁偱丄壓恾乮們乯偺夞楬偼弌椡揹棳偑戝偒偔側傝偡偓偰巊偊側偄帠偵怗傟傑偟偨丅偙偙偱偼偙偺傛偆偵丄僆儁傾儞僾偑弌椡偱偒傞嵟戝偺揹棳偵偮偄偰愢柧偟傑偡丅

偝偰丄壓恾偺傛偆偵僆儁傾儞僾偺弌椡傪怳傝愗傜偣丄弌椡偵愙懕偟偨掞峈偺抣傪彫偝偔偡傞偲丄僆儁傾儞僾偐傜弌椡偝傟傞揹棳偑憹壛偟傑偡丅
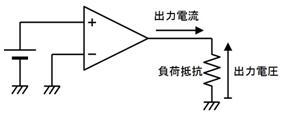
壓恾偼俶俰俵係俆俉侽傪亇侾俆倁偺俀揹尮偱巊梡偟偨応崌偺丄嵟崅乛嵟掅弌椡揹埑偲弌椡揹棳偺僌儔僼偱偡丅僾儔僗懁偵拲栚偡傞偲丄揹棳偑侾倣俙偺応崌偼侾係倁掱搙偺揹埑偑弌偣傑偡偑丄係侽倣俙偱偼侾俁倁丄俋侽倣俙偱偼俇倁偟偐弌椡偱偒側偄偙偲偑暘傝傑偡丅
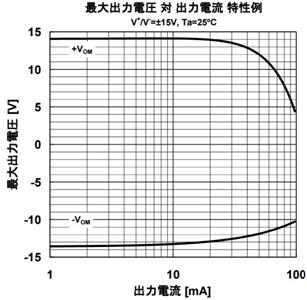
偙偺忬嫷傪惍棟偟偨壓昞偵帵偟傑偡丅偮傑傝丄僆儁傾儞僾偵偼揹棳傪棳偡擻椡偵尷奅偑偁傝丄柍棟偵弌椡揹棳傪憹傗偦偆偲偡傞偲丄僆儁傾儞僾偑晧偗偰丄弌椡揹埑偑壓偑偭偰偟傑偄傑偡丅
壓昞偐傜堦尒丄嵟崅弌椡揹埑偝偊変枬偡傟偽丄傛傝戝偒側弌椡揹棳傪棳偡偙偲偑偱偒傞傛偆偵傕巚偊傑偡丅偲偙傠偑丄僆儁傾儞僾偑夁擬偡傞偨傔丄偦偺傛偆側巊偄曽偵偼拲堄偑昁梫偱偡丅
|
弌椡揹棳
|
嵟崅弌椡揹埑
|
晧壸掞峈
|
徚旓揹椡
|
|
侾倣俙
|
侾係倁
|
侾係倁亐侾倣俙亖侾係倠兌
|
侾倁亊侾倣俙亖侾倣倂
|
|
係侽倣俙
|
侾俁倁
|
侾俁倁亐係侽倣俙亖俁俁侽兌
|
俀倁亊係侽倣俙亖俉侽倣倂
|
|
俋侽倣俙
|
俇倁
|
俇倁亐俋侽倣俙亖俇俇兌
|
俋倁亊俋侽倣俙亖俉侾侽倣倂
|
側偤側傜椺偊偽丄俋侽倣俙偺弌椡揹棳傪庢傝弌偟偰偄傞偲偒丄壓恾偵帵偡傛偆偵丄僆儁傾儞僾撪晹偺慺巕偼掞峈偲偟偰摥偄偰偄傑偡丅偦偟偰丄偙偺掞峈偱徚旓偡傞揹椡偱僆儁傾儞僾偑敪擬偟傑偡丅壓恾偺椺偱偼丄俇倁傪弌椡偟偰偄傞偲偒丄撪晹偺掞峈乮慺巕乯偵偼俋倁偺揹埑偑壛傢傝丄俋侽倣俙偺揹棳偑棳傟偰偄傞偨傔丄俉侾侽倣倂偺揹椡偑徚旓偝傟偰偄傑偡丅偙偺傛偆側丄弌椡揹棳枅偺徚旓揹椡傪忋昞偺乽徚旓揹椡乿偺楍偵帵偟傑偡丅
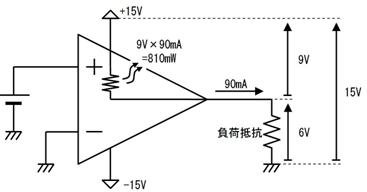
僆儁傾儞僾偼徚旓揹椡偑戝偒偔側傞偲師戞偵寖偟偔敪擬偟丄偮偄偵偼擬偱夡傟偰偟傑偄傑偡丅壓恾偼俶俰俵係俆俉侽偺愨懳嵟戝掕奿偱偡丅
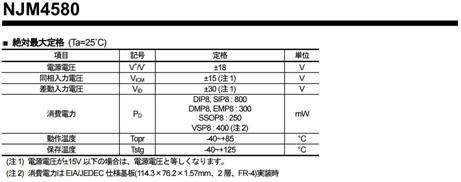
忋昞偵傛傟偽丄俢俬俹俉宍僷僢働乕僕偺応崌丄俉侽侽倣倂偺揹椡傪堦弖偱傕徚旓偝偣傞偲乽偄偮夡傟偰傕抦傜傫乿偲婰嵹偝傟偰偄傑偡丅
廬偭偰丄婛偵弎傋偨俋侽倣俙弌椡揹棳傪庢傝弌偟偨応崌偺俉侾侽倣倂偺徚旓揹椡偼丄愨懳嵟戝掕奿傪挻偊偰偄傞偨傔堦弖偨傝偲傕嫋偝傟傑偣傫丅偮傑傝丄俋侽倣俙偺弌椡揹棳偼丄乽棳偡擻椡偼偁傞偑丄棳偡偲夡傟傞乿帠偑暘傝傑偡丅
偙偺傛偆偵丄僆儁傾儞僾偺嵟戝弌椡揹棳偼丄僨乕僞僔乕僩偵婰嵹偝傟偨乽嵟戝弌椡揹棳乿偺抣偑尷奅偱偼偁傝傑偡偑丄乮僆儁傾儞僾偑夁擬偟偰夡傟側偄傛偆偵乯徚旓揹椡偑掕奿傪廫暘壓夞傞偙偲傕妋擣偟偰棙梡偟傑偡丅傑偨丄侾偮偺僷僢働乕僕偵暋悢偺僆儁傾儞僾偑擖偭偰偄傞応崌丄慡偰偺僆儁傾儞僾偺徚旓揹椡偺崌寁偑掕奿傪廫暘壓夞傞傛偆偵専摙偟傑偡丅
俁.侾. 楙廗
壓恾偺傛偆偵丄俶俰俵係俆俉侽傪亇侾俆倁揹尮偱巊梡偟丄弌椡傪亄懁偵怳傝愗傜偣偰丄俇侽倣俙偺揹棳傪庢傝弌偟偟傑偟偨丅婛弌偺僌儔僼傪棙梡偟偰丄弌椡揹埑傪媮傔丄徚旓揹椡傪寁嶼偟偰偔偩偝偄丅
弌椡揹埑丂丂丂丂倁丂徚旓揹椡丂丂丂丂倣倂
俁.俀. 摎
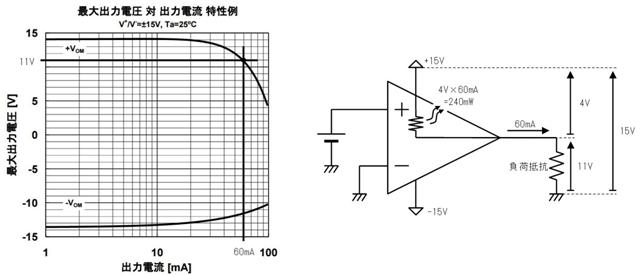
弌椡揹埑丂丂侾侾倁丂徚旓揹椡丂俀係侽倣倂
忋婰偺僌儔僼偐傜丄俇侽倣俙帪偺亄懁弌椡揹埑傪撉傒庢傞偲侾侾倁丅僆儁傾儞僾偺撪晹慺巕偵偼係倁偺揹埑偑壛傢偭偰偍傝丄俇侽倣俙偺揹棳偑棳傟偰偄傞偐傜丄俀係侽倣倂偺揹椡偑徚旓偝傟偰偄傞丅
係. 擖椡僆僼僙僢僩揹埑
壓恾偺夞楬偼丄棟憐僆儁傾儞僾偱偁傟偽丄惓妋偵侽倁傪弌椡偡傞敜偱偡丅偲偙傠偑壓恾偱偼丄侾倁偑弌椡偝傟偰偄傑偡丅
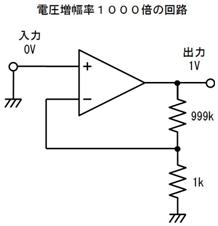
偙偺夞楬偱偼僆儁傾儞僾偺乽棟憐揑偱側偄乿晹暘偺拞偱乽擖椡僆僼僙僢僩揹埑乿乮埲壓丄僆僼僙僢僩乯偑栤戣偵側傝傑偡丅
偝偰丄僆儁傾儞僾偺廳梫側惈幙嘆偵乽晧婣娨偺夞楬偱偼丄亄擖椡偲亅擖椡偺揹埑偼摨偠乿偑偁傝傑偟偨丅偲偙傠偑幚嵺偵偼丄亄擖椡偲亅擖椡偺娫偵嬐偐側揹埑偺嵎偑惗偠傑偡丅偙偺揹埑偑僆僼僙僢僩偱偡丅
僆僼僙僢僩偼丄壓恾偵帵偡傛偆偵丄拞偺恖偑棫偮彴偵惗偠偨乽抜嵎乿偺傛偆側傕偺偱偡丅拞偺恖偼彴偺崅偝傪亄擖椡偵傄偭偨傝偁傢偣偨偮傕傝偱傕丄奜偐傜尒傞偲丄亅擖椡偲亄擖椡偺娫偵偼嵎偑惗偠偰偟傑偄傑偡丅
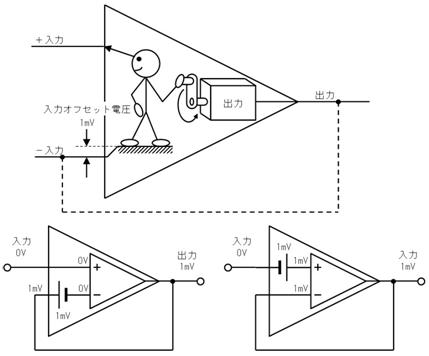
夞楬恾偱偼丄僆僼僙僢僩傪忋恾壓懁偺傛偆偵丄擖椡抂巕偵憓擖偝傟偨揹抮偱昞偡偙偲偑偱偒傑偡丅揹抮偼亅擖椡偵憓擖偟偰傕丄亄擖椡偵憓擖偟偰傕偐傑偄傑偣傫丅傑偨揹抮偺嬌惈傕丄偳偪傜岦偒偱傕峔偄傑偣傫丅
忋恾偱偼侾倣倁偺揹抮偑憓擖偝傟偨乮侾倣倁偺僆僼僙僢僩偑偁偭偨乯偨傔偵丄杮棃侽倁偲側傞憹暆婍偺弌椡偑偵侾倣倁偑弌椡偝傟偰偄傑偡丅
偝偰丄僆僼僙僢僩偵偼丄屄懱嵎偑偁傞丄壏搙偱曄壔偡傞丄偲偄偆俀偮偺摿挜偑偁傝傑偡丅
壓昞偼乽俶俰俵俷俹俙俀俈俈乿乮摿偵僆僼僙僢僩傪彫偝偔偟偨昳庬偱偡乛俷俹俙俀俈俈偺僙僇儞僪僜乕僗乮偦偭偔傝偝傫乯乯偺僆僼僙僢僩揹埑偱偡丅乮俥僌儗乕僪昳偺乯昗弨抣偱侾侽兪倁偲彫偝偔梷偊傜傟偰偄傞偺偑暘傝傑偡丅
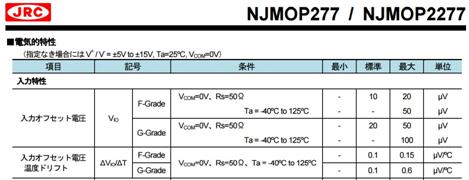
壓恾偼摨僆儁傾儞僾偺僆僼僙僢僩揹埑偺屄懱嵎偱偡丅摨恾偺僌儔僼傪尒傞偲僆僼僙僢僩揹埑偼屄懱枅偵亅係侽兪倁乣亄係侽兪倁偺斖埻偱條乆偵堎側傞偙偲偑暘傝傑偡丅
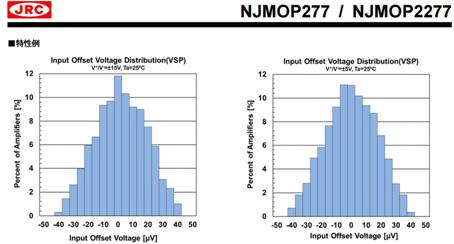
偮傑傝丄昗弨偺僆僼僙僢僩揹埑偑侾侽兪倁偟偐側偄乮俥僌儗乕僪偺乯俶俰俵俷俹俙俀俈俈傪峸擖偟偰傕丄塣偑埆偄偲僆僼僙僢僩偑係侽兪倁敪惗偡傞応崌傕偁傞偙偲偑暘傝傑偡丅乮媡偵塣偑椙偗傟偽丄杦偳僛儘偲偄偆応崌傕偁傝傑偡乯傕偪傠傫晄椙昳偱偼偁傝傑偣傫丅偙傟偑僆僼僙僢僩揹埑偺屄懱嵎偱偡丅
傑偨嵟弶偺昞偵偼丄擖椡僆僼僙僢僩揹埑壏搙僪儕僼僩乮埲壓丄壏搙僪儕僼僩乯傕帵偝傟偰偄傑偡丅壏搙僪儕僼僩偲偼丄壏搙偵傛傞僆僼僙僢僩偺曄壔偱偡丅
摨昞偵傛傟偽丄乮俥僌儗乕僪昳偱乯壏搙偑侾亷曄壔偡傞偲丄嵟戝偱擖椡僆僼僙僢僩偑侽丏侾俆兪倁曄壔偡傞偙偲偑傢偐傝傑偡丅偨偲偊偽丄壏搙偑係侽亷曄壔偡傞偲丄嵟埆偱俇兪倁掱搙偺僆僼僙僢僩揹埑偺曄壔偑偁傝傑偡丅
偙偺傛偆偵丄僆僼僙僢僩偼彫偝側抣偱偡偑丄壓恾偺傛偆偵戝偒側憹暆棪傪帩偮夞楬偱偼丄僆僼僙僢僩傕憹暆偝傟傞偨傔丄塭嬁偑戝偒偔側傝傑偡丅壓恾偼侾侽侽侽攞偺憹暆婍傪丄僆僼僙僢僩侾倣倁偺僆儁傾儞僾偱嶌偭偨椺偱偡丅
俇.侾. 楙廗乮僆僼僙僢僩偺塭嬁乯
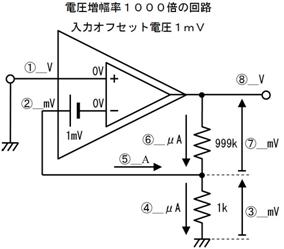
忋恾偺夞楬偵偮偄偰丄僆僼僙僢僩揹埑偺塭嬁傪挷傋傑偡丅壓昞偵彂偒側偑傜丄侽倁傪擖椡偟偨応崌偺弌椡揹埑傪峫偊偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡揹埑偼丄
|
侽倁
|
|
嘇
|
晧婣娨偺夞楬偩偐傜丄亄擖椡偲亅擖椡偺揹埑偼摨偠偵側傞敜偩偑丄侾倣倁偺僆僼僙僢僩偑偁傞偨傔丄儅僀僫僗擖椡抂巕偺揹埑偼丄
|
倣倁
|
|
嘊
|
侾倠兌偺椉抂揹埑偼丄
|
倣倁
|
|
嘋
|
侾倠兌偵棳傟傞揹棳偼丄
|
兪俙
|
|
嘍
|
僆儁傾儞僾偺擖椡抂巕偵棳傟傞揹棳偼丄
乮偙偙偱偼擖椡僶僀傾僗揹棳傪柍帇偟偰乯
|
俙
|
|
嘐
|
俋俋俋倠偵棳傟傞揹棳偼丄
|
兪俙
|
|
嘑
|
俋俋俋倠偵敪惗偡傞揹埑偼丄
|
倣倁
|
|
嘒
|
弌椡揹埑偼丄
|
倁
|
俇.俀. 摎
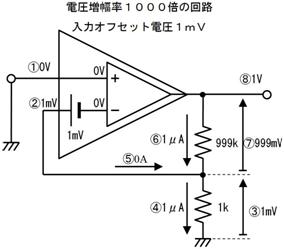
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡揹埑偼丄
|
侽倁
|
|
嘇
|
晧婣娨偺夞楬偩偐傜丄亄擖椡偲亅擖椡偺揹埑偼摨偠偵側傞敜偩偑丄侾倣倁偺僆僼僙僢僩偑偁傞偨傔丄儅僀僫僗擖椡抂巕偺揹埑偼丄
|
侾倣倁
|
|
嘊
|
侾倠兌偺椉抂揹埑偼丄
|
侾倣倁
|
|
嘋
|
侾倠兌偵棳傟傞揹棳偼丄
|
侾兪俙
|
|
嘍
|
僆儁傾儞僾偺擖椡抂巕偵棳傟傞揹棳偼丄
乮偙偙偱偼擖椡僶僀傾僗揹棳傪柍帇偟偰乯
|
侽俙
|
|
嘐
|
俋俋俋倠偵棳傟傞揹棳偼丄
|
侾兪俙
|
|
嘑
|
俋俋俋倠偵敪惗偡傞揹埑偼丄
|
俋俋俋倣倁
|
|
嘒
|
弌椡揹埑偼丄
|
侾倁
|
偙偺傛偆偵丄崅偄惛搙偑昁梫側夞楬傗丄崅攞棪偺憹暆婍丄彫偝側揹埑傪埖偆夞楬摍偱偼丄僆僼僙僢僩偺塭嬁偑戝偒偔尰傟傞偺偱丄懳嶔偑昁梫偵側傝傑偡丅
僆僼僙僢僩懳嶔偵偼師昞偵帵偡傛偆偵乽夞楬偱懳嶔偡傞乿偲乽僆儁傾儞僾偱懳嶔偡傞乿偺俀僞僀僾偑偁傝傑偡丅嵟嬤偼丄僆僼僙僢僩偺彫偝側僆儁傾儞僾傕懨摉側壙奿偱庤偵擖傞偺偱乽僆儁傾儞僾偱懳嶔偡傞乿偑庡棳偱偡丅
|
曽朄
|
夞楬偱懳嶔偡傞
|
僆儁傾儞僾偱懳嶔偡傞
|
|
奣梫
|
僆僼僙僢僩揹埑傪挷愡偡傞夞楬傪捛壛偡傞丅
|
僆僼僙僢僩揹埑偺彫偝側僆儁傾儞僾傪棙梡偡傞丅
|
|
旓梡
|
挷愡夞楬偺旓梡偑昁梫
|
妱崅側僆儁傾儞僾偑昁梫
|
|
庤娫
|
挷惍偑昁梫
|
挷惍偼晄梫
|
婛偵愢柧偟偨傛偆偵丄僆僼僙僢僩偼摨偠昳庬偱傕屄懱嵎偱戝偒偔堎側傝傑偡丅偙偺偨傔丄夞楬偱懳嶔偡傞応崌偼丄偁傜偐偠傔抣傪尒墇偟偰乮寛傔懪偪偱乯懳嶔偟偰偍偔偙偲偼偱偒偢丄敿屌掕掞峈傪梡偄偰丄屄暿偵挷惍偡傞昁梫偑偁傝傑偡丅
僆僼僙僢僩揹埑傪丄夞楬偱懳嶔偟偰挷惍偟偰傕丄壏搙偑曄壔偡傞偲壏搙僪儕僼僩偑敪惗偟偰丄挷惍偑僘儗偰偟傑偄丄僆僼僙僢僩偺塭嬁偑嵞敪偟傑偡丅摿偵憰抲偺揹尮傪搳擖偟偨屻偼丄嵟弶偼幒壏偱偁偭偨慺巕偑丄棳傟傞揹棳偵傛偭偰壏傑傞偺偱丄壏搙僪儕僼僩偑栚棫偪傑偡丅
壏搙僪儕僼僩偺懳嶔偼乽壏搙僪儕僼僩偺彫偝側僆儁傾儞僾傪慖傇乿偙偲偱峴偄傑偡丅
夁嫀偵偼壏搙僪儕僼僩偺塭嬁傪懪偪徚偡夞楬傪愝偗偨傝丄僆儁傾儞僾傪堦掕偺壏搙偵曐偮乽俬俠僆乕僽儞乿傪巊梡偟偨傝偟傑偟偨偑丄壏搙僪儕僼僩偺彫偝側僆儁傾儞僾偑懨摉側壙奿偵側偭偨偨傔丄偁傑傝棙梡偝傟傑偣傫丅
僆僼僙僢僩偲壏搙僪儕僼僩偺彮側偄僆儁傾儞僾傪慖傇偙偲偱丄僆僼僙僢僩偺塭嬁傪柍偔偡偺偑丄尰嵼偼堦斒揑偱偡丅偟偐偟丄揹巕岺嶌偱偼乽庤帩偪偺晹昳偱帋偟偰傒偨偄乿乽偲傝偁偊偢摦偔偐僠僃僢僋偟偨偄乿偲偄偆応崌傕懡偔丄奜晅偗偺夞楬偱僆僼僙僢僩傪挷惍偡傞曽朄傪愢柧偟傑偡丅
僆儁傾儞僾偼侾偮偺僷僢働乕僕偵丄侾偮擖傝丄俀偮擖傝丄係偮擖傝丄偲暋悢撪憼偟偨傕偺偑嶌傜傟偰偄傑偡丅侾偮擖傝偺僆儁傾儞僾偺拞偵偼乽僆僼僙僢僩挷惍乮僆僼僙僢僩僰儖乯抂巕乿傪旛偊偰偄傞傕偺偑偁傝傑偡丅
壓恾偼俴俥係侾侾偺僺儞愙懕恾偺椺偱丄侾斣僺儞偲俆斣僺儞偑乽僆僼僙僢僩挷惍抂巕乿偱偡丅挷惍傪峴傢側偄応崌偼丄側偵傕愙懕偣偢丄峴偆偲偒偼僨乕僞僔乕僩偺巜帵偵偟偨偑偭偰敿屌掕掞峈摍傪愙懕偟傑偡丅
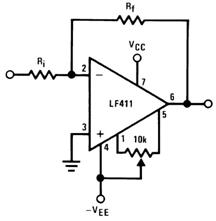
僆僼僙僢僩偺彮側偄僆儁傾儞僾偺廩幚丄晹昳揰悢偺嶍尭丄挷惍僐僗僩偺掅尭摍偺棟桼偱丄僆僼僙僢僩挷惍抂巕偺偁傞僆儁傾儞僾偼尭偭偰偄傑偡偟丄棙梡偺婡夛傕彮側偔側偭偰偄傑偡丅
壓恾偵揰慄偱帵偡夞楬偑丄僆僼僙僢僩挷惍夞楬偱偡丅揰慄偺夞楬偑摦嶌偟偰偄側偄応崌丄侽倁傪擖椡偟偰傕丄俇倣倁偺僆僼僙僢僩偑侾侽侽侽攞偵憹暆偝傟偰丄俇倁偑弌椡偝傟傑偡丅
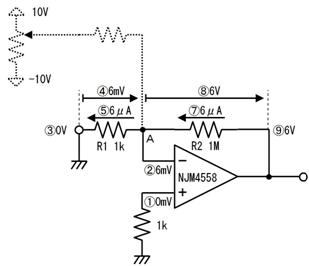
偦偙偱丄壓恾偵丄僆僼僙僢僩懳嶔夞楬傪摦嶌偝偣偨忬懺傪帵偟傑偡丅
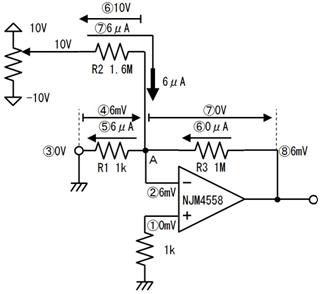
俇倣倁偺僆僼僙僢僩偑尨場偲側傝丄俼侾偼忋恾俙揰偐傜丄俇兪傾儞儁傾偺揹棳傪媧偄崬傒傑偡丅偦偙偱丄俼俀偐傜俙揰偵岦偐偭偰丄摨偠俇兪俙傪棳偟崬傓偙偲偱丄俼俁偵棳傟傞揹棳傪僛儘偵挷惍偱偒傑偡丅乮僉儖僸揹棳懃傪俙揰偵巊偄傑偡乯
傑偨丄旕斀揮憹暆夞楬偺応崌偼丄壓恾偺曽朄偱僆僼僙僢僩傪挷惍偟傑偡丅
侾侽.侾. 楙廗
壓恾傪尒側偑傜壓昞偵彂偒崬傒丄僆僼僙僢僩挷惍偺曽朄傪峫偊傑偡丅
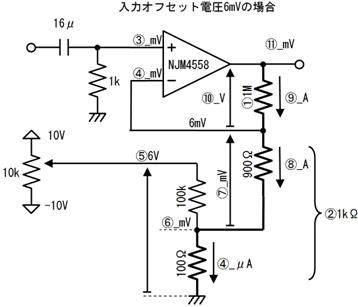
|
斣崋
|
幙栤
|
抣
|
|
嘆嘇
|
婣娨掞峈偺暘埑斾偼嘆偲嘇傛傝丄
|
栺侾侽侽侽暘偺侾
|
|
|
偙偺偨傔忋恾偺夞楬偺憹暆棪偼丄
|
栺侾侽侽侽攞
|
|
嘊
|
亄擖椡抂巕偼侾倠兌偱愙抧偝傟偰偄傞偺偱丄
擖椡僶僀傾僗揹棳偺塭嬁傪峫偊側偗傟偽丄
|
倣倁
|
|
嘋
|
晧婣娨偺夞楬偩偐傜亄擖椡偲亅擖椡偼摨偠揹埑偵側傞敜偩偑丄俇倣倁偺僆僼僙僢僩偑偁傞偲偟偰丄亅擖椡抂巕偺揹埑偼乮亄偺揹埑偑尰傟偨偲偡傞偲乯
|
倣倁
|
|
嘍
|
敿屌掕掞峈偐傜庢傝弌偟偨揹埑偼丄
|
俇倁
|
|
嘐
|
忋偺嘍偺揹埑偑侾侽侽倠偲侾侽侽兌偱暘埑偝傟偰丄侾侽侽兌偺忋懁偺揹埑偼丄
|
栺丂丂丂倣倁
|
|
嘑
|
俋侽侽兌偺椉抂揹埑偼丄
|
倁
|
|
嘒
|
俋侽侽兌偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘓
|
侾俵兌偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘔
|
侾俵兌偺椉抂揹埑偼丄
|
倁
|
|
嘕
|
弌椡揹埑偼丄
|
倣倁
|
侾侽.俀. 摎
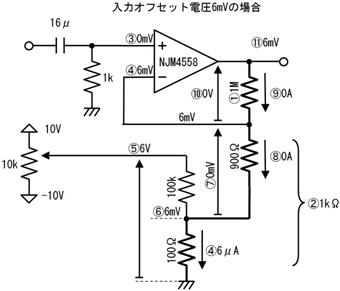
|
斣崋
|
幙栤
|
抣
|
|
嘆嘇
|
婣娨掞峈偺暘埑斾偼嘆偲嘇傛傝丄
|
栺侾侽侽侽暘偺侾
|
|
|
偙偺偨傔忋恾偺夞楬偺憹暆棪偼丄
|
栺侾侽侽侽攞
|
|
嘊
|
亄擖椡抂巕偼侾倠兌偱愙抧偝傟偰偄傞偺偱丄
擖椡僶僀傾僗揹棳偺塭嬁傪峫偊側偗傟偽丄
|
侽倣倁
|
|
嘋
|
晧婣娨偺夞楬偩偐傜亄擖椡偲亅擖椡偼摨偠揹埑偵側傞敜偩偑丄俇倣倁偺僆僼僙僢僩偑偁傞偲偟偰丄亅擖椡抂巕偺揹埑偼乮亄偺揹埑偑尰傟偨偲偡傞偲乯
|
俇倣倁
|
|
嘍
|
敿屌掕掞峈偐傜庢傝弌偟偨揹埑偼丄
|
俇倁
|
|
嘐
|
忋偺揹埑偑侾侽侽倠偲侾侽侽兌偱暘埑偝傟偰丄侾侽侽兌偺忋懁偺揹埑偼丄
|
栺俇倣倁
|
|
嘑
|
俋侽侽兌偺椉抂揹埑偼丄
|
侽倁
|
|
嘒
|
俋侽侽兌偵棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘓
|
侾俵兌偵棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘔
|
侾俵兌偺椉抂揹埑偼丄
|
侽倁
|
|
嘕
|
弌椡揹埑偼丄
|
俇倣倁
|
侾侾. 岎棳憹暆夞楬偺僆僼僙僢僩懳嶔
僆僼僙僢僩偺戝偒側僆儁傾儞僾偱傕丄岎棳憹暆夞楬偱偁傟偽丄柍挷惍偱僆僼僙僢僩偺塭嬁傪梷偊傞偙偲偑偱偒傑偡丅壓恾偼丄懳嶔傪峴偭偰偄側偄岎棳憹暆夞楬偱偡丅
侾侾.侾. 楙廗
壓恾偺夞楬偺摦嶌傪丄壓昞偵婰擖偟側偑傜峫偊丄弌椡僆僼僙僢僩揹埑傪媮傔偰壓偝偄丅
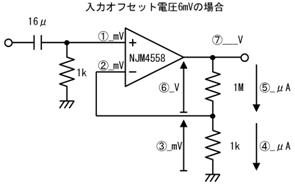
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡揹埑偼丄侾倠兌傪捠偠偰傾乕僗偝傟偰偄傞偐傜丄
|
倁
|
|
嘇
|
杮棃晧婣娨夞楬偱偼亄擖椡偲亅擖椡偺揹埑偼摍偟偄偑丄
偙偺僆儁傾儞僾偺嵟戝僆僼僙僢僩揹埑偼俇倣倁偩偐傜丄壖偵亅擖椡偵惓偺僆僼僙僢僩揹埑偑尰傟傞偲偡傟偽丄
|
倣倁
|
|
嘊
|
侾俵兌偺壓懁偵偁傞丄侾倠兌偺椉抂揹埑偼丄
|
倣倁
|
|
嘋
|
偙偺侾倠兌偵棳傟傞揹棳偼丄
|
兪俙
|
|
嘍
|
擖椡僶僀傾僗揹棳傪柍帇偡傟偽丄侾俵兌偵棳傟傞揹棳偼丄
|
兪俙
|
|
嘐
|
侾俵兌偺椉抂揹埑偼丄
|
倁
|
|
嘑
|
弌椡揹埑偼丄
|
倁
|
侾侾.俀. 摎
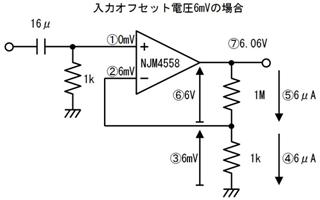
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡揹埑偼丄侾倠兌傪捠偠偰傾乕僗偝傟偰偄傞偐傜丄
|
侽倁
|
|
嘇
|
杮棃晧婣娨夞楬偱偼亄擖椡偲亅擖椡偺揹埑偼摍偟偄偑丄
偙偺僆儁傾儞僾偺嵟戝僆僼僙僢僩揹埑偼俇倣倁偩偐傜丄壖偵亅擖椡偵惓偺僆僼僙僢僩揹埑偑尰傟傞偲偡傟偽丄
|
俇倣倁
|
|
嘊
|
侾俵兌偺壓懁偵偁傞丄侾倠兌偺椉抂揹埑偼丄
|
俇倣倁
|
|
嘋
|
偙偺侾倠兌偵棳傟傞揹棳偼丄
|
俇兪俙
|
|
嘍
|
擖椡僶僀傾僗揹棳傪柍帇偡傟偽丄侾俵兌偵棳傟傞揹棳偼丄
|
俇兪俙
|
|
嘐
|
侾俵兌偺椉抂揹埑偼丄
|
俇倁
|
|
嘑
|
弌椡揹埑偼丄
|
俇丏侽侽俇倁
|
偲側傝丄僆僼僙僢僩偑栺侾侽侽侽攞偵奼戝偝傟偰丄俇倁偲側偭偰弌椡偵偁傜傢傟傑偟偨丅
岎棳夞楬偺応崌乽捈棳偼憹暆偟側偔偰椙偄乿偲偄偆敳偗摴偑偁傝傑偡偐傜丄壓恾偺傛偆側夞楬傪梡偄偰丄岎棳偱偼侾侽侽侽攞丄捈棳偱偼侾攞丄偲偄偆嬶崌偵丄捈棳偺憹暆棪偩偗傪壓偘傞偙偲偱丄弌椡揹埑偺僆僼僙僢僩傪彫偝偔偟傑偡丅
侾侾.俁. 楙廗
偱偼丄壓恾傪尒側偑傜丄壓昞偵彂偒崬傫偱丄夞楬偺摦嶌傪峫偊傑偡丅
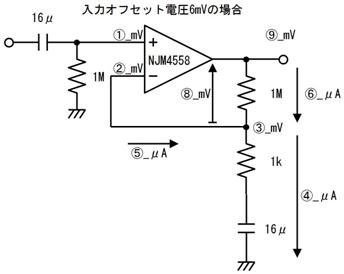
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡揹埑偼丄侾俵兌傪捠偠偰傾乕僗偝傟偰偄傞偐傜丄
|
倁
|
|
嘇
|
杮棃晧婣娨夞楬偱偼亄擖椡偲亅擖椡偺揹埑偼摍偟偄偑丄
偙偺僆儁傾儞僾偺嵟戝僆僼僙僢僩揹埑偼俇倣倁偩偐傜丄壖偵亅擖椡偵惓偺僆僼僙僢僩揹埑偑尰傟傞偲偡傟偽丄
|
倣倁
|
|
嘊
|
侾俵兌偺壓懁偵偁傞丄侾倠兌偲侾俇兪俥偺捈楍夞楬偵壛傢傞揹埑偼丄
|
倣倁
|
|
嘋
|
僐儞僨儞僒偼捈棳傪捠偝側偄偐傜丄侾倠偲侾俇兪偺捈楍夞楬偵棳傟傞揹棳偼丄
|
兪俙
|
|
嘍
|
擖椡僶僀傾僗揹棳傪柍帇偡傟偽丄亅擖椡偐傜棳傟傞揹棳偼丄
|
兪俙
|
|
嘐
|
侾俵兌偵棳傟傞揹棳偼丄
|
兪俙
|
|
嘐
|
侾俵兌偺椉抂揹埑偼丄
|
倁
|
|
嘑
|
弌椡揹埑偼丄
|
倣倁
|
侾侾.係. 摎
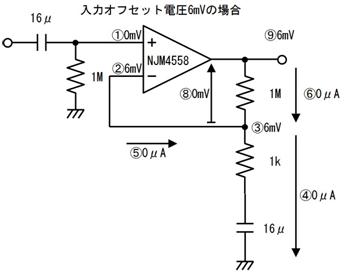
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡揹埑偼丄侾俵兌傪捠偠偰傾乕僗偝傟偰偄傞偐傜丄
|
侽倁
|
|
嘇
|
杮棃晧婣娨夞楬偱偼亄擖椡偲亅擖椡偺揹埑偼摍偟偄偑丄
偙偺僆儁傾儞僾偺嵟戝僆僼僙僢僩揹埑偼俇倣倁偩偐傜丄壖偵亅擖椡偵惓偺僆僼僙僢僩揹埑偑尰傟傞偲偡傟偽丄
|
俇倣倁
|
|
嘊
|
侾俵兌偺壓懁偵偁傞丄侾倠兌偲侾俇兪俥偺捈楍夞楬偵壛傢傞揹埑偼丄
|
俇倣倁
|
|
嘋
|
僐儞僨儞僒偼捈棳傪捠偝側偄偐傜丄侾倠偲侾俇兪偺捈楍夞楬偵棳傟傞揹棳偼丄
|
侽兪俙
|
|
嘍
|
擖椡僶僀傾僗揹棳傪柍帇偡傟偽丄亅擖椡偐傜棳傟傞揹棳偼丄
|
侽兪俙
|
|
嘐
|
侾俵兌偵棳傟傞揹棳偼丄
|
侽兪俙
|
|
嘐
|
侾俵兌偺椉抂揹埑偼丄
|
侽倁
|
|
嘑
|
弌椡揹埑偼丄
|
俇倣倁
|
偙偺傛偆偵丄婣娨夞楬偵僐儞僨儞僒傪巊偆偙偲偱丄捈棳偺憹暆棪傪侾偵壓偘丄僆僼僙僢僩揹埑傕侾攞偱偟偐弌椡偵塭嬁偟側偄傛偆偵夵慞偱偒傑偡丅偙偺憹暆婍偼侾乛乮俀兾亊侾倠亊侾俇兪俥乯埲壓偺廃攇悢偱偼憁暈棪偑壓偑偭偰峴偒傑偡丅
侾俀. 嵟崅乛嵟掅弌椡揹埑
僆儁傾儞僾偺廳梫側惈幙偵丄嘇亄擖椡 亜
亅擖椡側傜丄弌椡偼亄揹尮傑偱怳傝愗傞丄傑偨丄嘊亄擖椡 亙 亅擖椡側傜丄弌椡偼亅揹尮傑偱怳傝愗傞丄偲偄偆偺偑偁傝傑偟偨丅
壓恾嵍偼柍埨掕儅儖僠僶僀僽儗乕僞偺夞楬丄塃偼棟憐僆儁傾儞僾偺摦嶌攇宍偱偡丅
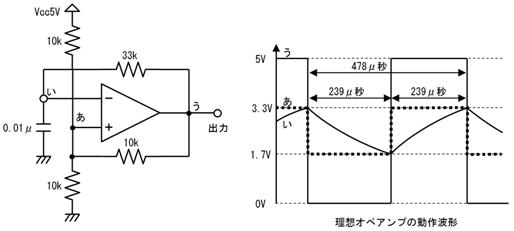
偲偙傠偑丄幚嵺偵忋恾偺夞楬傪嶌偭偰摦嶌偝偣傞偲丄壓恾偵帵偡偲偍傝丄僆儁傾儞僾偺昳庬偵傛偭偰攇宍偑堎側傝傑偡丅摨恾偱偼丄乽偄乿偺僐儞僨儞僒偺揹埑攇宍偲丄乽偆乿偺弌椡攇宍傪昞帵偟偰偄傑偡丅
|
嘆儗僀儖丒僩僁丒儗僀儖僞僀僾
|
嘇斈梡僞僀僾
|
嘊斈梡扨揹尮僞僀僾
|
|
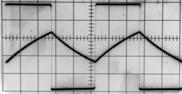
|

|
|
|
俴俵俠俇係俉俀
|
俶俰俵係俆俉侽
|
俴俵俁俆俉
|
乽偆乿偺弌椡攇宍偵拲栚偡傞偲丄嘆偺儗僀儖僩僁儗僀儖僞僀僾偱偼傎傏棟憐捠傝偵侽倁乣俆倁傑偱怳傟偰偄傑偡偑丄斈梡僞僀僾偱偼侾丏俁乣係丏俀倁掱搙丄斈梡扨揹尮僞僀僾偱偼侽丏俈乣俁丏俇倁掱搙偟偐怳傟偰偄傑偣傫丅
偙偺傛偆偵僆儁傾儞僾偼昳庬傗忦審偵傛偭偰丄弌椡偱偒傞嵟崅偺揹埑偲嵟掅偺揹埑偑惂尷偝傟傑偡丅偙偺揹埑傪丄嵟崅弌椡揹埑乮倁俷俫乯丄嵟掅弌椡揹埑乮倁俷俴乯偲屇傫偱偄傑偡丅乮偙偺俀偮傪憤偠偰丄嵟戝弌椡揹埑偲屇傇偙偲傕偁傝傑偡乯
弌椡揹埑偼揹尮揹埑傪墇偊傞偙偲偼偱偒傑偣傫偐傜丄嵟崅乛嵟掅弌椡揹埑偼丄壓恾偵帵偡傛偆偵丄揹尮揹埑偱寛傑傝傑偡丅乮偦偺懠丄壏搙傗弌椡偡傞揹棳偵傛偭偰懡彮曄壔偟傑偡乯
壓恾偼俶俰俵係俆俉侽偺揹尮揹埑偲嵟崅乛嵟掅弌椡揹埑偺娭學偱偡丅亇揹尮傪巊梡偟偨応崌偺僌儔僼偱偡偐傜丄偨偲偊偽俆倁扨堦揹尮偺応崌亇俀丏俆倁偲峫偊偰僌儔僼傪巊偄傑偡丅
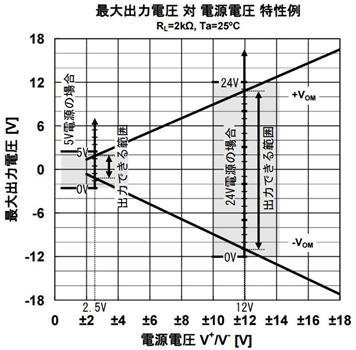
栚惙傝偑峳偔偰尒擄偄偱偡偑丄忋恾嵍懁偵奃怓偱帵偡揹尮揹埑俆倁扨堦乮忋偺僌儔僼偱偼亇俀丏俆倁偵憡摉乯偺晹暘偱偼丄嵟崅乛嵟掅弌椡揹埑偼侾丏俁乣係丏俀倁掱搙偱丄偦偺嵎乮弌椡偱偒傞怳暆乯偼俀丏俈倁偲恏偆偠偰撉傓偙偲偑偱偒傑偡丅揹尮揹埑偑俆倁偱弌椡怳暆偑俀丏俈倁偱偡偐傜丄揹尮揹埑偺俆俉亾掱搙偺怳暆偟偐庢傟側偄帠偑暘傝傑偡丅
媡偵丄忋恾塃懁偵奃怓偱帵偡揹尮揹埑俀係倁扨堦乮忋偺僌儔僼偱偼亇侾俀倁偵憡摉乯偺晹暘偱偼丄嵟崅乛嵟掅弌椡揹埑偼丄侾丏俀乣俀俀丏俉倁掱搙偱丄偦偺嵎偼俀侾丏俇倁偁傝丄揹尮揹埑偺俋侽亾掱搙偺怳暆偑庢傟傞帠偑傢偐傝傑偡丅
偮傑傝丄揹尮揹埑偑崅偄偲丄棙梡偱偒傞妱崌偑戝偒偔側傝傑偡丅偙偺尰徾偼壓恾偵帵偡傛偆偵丄僆儁傾儞僾偺昳庬枅偵乽亄懁偺巊偊側偄揹埑乿偲乽亅懁偺巊偊側偄揹埑乿偑偁傝丄偙傟傜偼丄揹尮揹埑傗晧壸偱懡彮偼曄壔偡傞偗傟偳傕丄偩偄偨偄堦掕偲峫偊傞偲暘傝堈偄偱偡丅
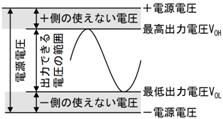
偝偰嵞搙偙偺崁偺嵟弶偵帵偟偨俁枃偺幨恀偵栠傞偲丄嵟崅乛嵟掅弌椡揹埑偺塭嬁偱丄忋偺僗儗僢僔儑儖僪傗壓偺僗儗僢僔儑儖僪傕曄壔偟丄偦偺寢壥丄敪怳廃婜偵傕塭嬁偟偰偄傞偙偲偑暘傝傑偡丅
偱偡偐傜丄惓妋側摦嶌傪寁嶼偡傞偲偒偵偼乽嘇亄擖椡 亜
亅擖椡側傜丄弌椡偼嵟崅弌椡揹埑傑偱怳傝愗傞丄傑偨丄嘊亄擖椡 亙 亅擖椡側傜丄弌椡偼嵟掅弌椡揹埑傑偱怳傝愗傞乿偲峫偊傑偡丅
侾俁. 摨憡擖椡揹埑斖埻
弌椡偱偒傞揹埑偵斖埻偑偁傞傛偆偵丄擖椡偱偒傞揹埑偵傕斖埻偑偁傝傑偡丅擖椡偱偒傞揹埑偺惂尷偵偼俀庬椶偁傝傑偡丅摨憡擖椡揹埑斖埻偲嵎摦擖椡揹埑斖埻偱偡丅偝傜偵丄擖椡偟偰傕夡傟側偄斖埻乮愨懳嵟戝掕奿乯偲惓忢偵摦嶌偡傞斖埻乮揹婥揑摿惈乯偑偁傝傑偡丅
壓恾偺傛偆側晧婣娨偺夞楬偑惓忢偵摦嶌偟偰偄傞偲偒丄亄擖椡抂巕偲亅擖椡抂巕偼摨偠揹埑偵側傝傑偡丅偙偺傛偆側忬懺偱擖椡偵壛偊傞揹埑偑丄摨憡擖椡揹埑偱偡丅
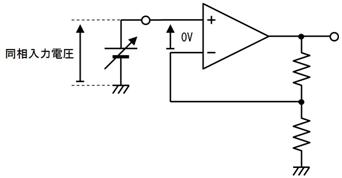
偮傑傝丄晧婣娨偺妡偐偭偨夞楬偺傛偆偵丄亄擖椡偲亅擖椡偑摨偠揹埑偺応崌偵応崌偵丄擖椡偱偒傞乮惓偟偔摦嶌偡傞乯擖椡揹埑偺斖埻偑摨憡擖椡揹埑斖埻偱偡丅
壓昞偼俶俰俵俀侾侾係偺揹婥揑摿惈偱偡丅亇侾俆倁偺俀揹尮偺応崌丄昞偺俆峴栚偵傛傟偽丄嵟掅亇侾俀倁偮傑傝丄亅侾俀倁乣亄侾俀倁偺娫偱偁傟偽丄惓偟偔摦嶌偡傞偙偲偑暘傝傑偡丅
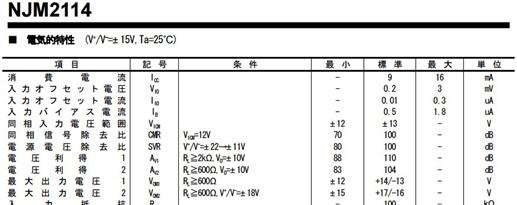
壓昞偼摨偠偔俀侾侾係偺愨懳嵟戝掕奿偱偡丅愨懳嵟戝掕奿偼乽堦弖偱傕墇偊偨傜偄偮夡傟偰傕抦傜傫丄偄傗丄嫲傜偔夡傟傞乿偲偄偆僊儕僊儕堦攖偺悢抣偱偡偐傜拲堄偑昁梫偱偡丅
壓昞俀峴栚偵帵偡傛偆偵丄俀侾侾係偺摨憡擖椡揹埑偺愨懳嵟戝掕奿偼揹尮揹埑偱偡丅偮傑傝丄亇侾俆倁偺俀揹尮偱巊梡偟偰偄傞偲偒丄堦弖偱傕亅侾俆倁傪壓夞傞丄偁傞偄偼丄堦弖偱傕亄侾俆倁傪墇偊傞偲乽夡傟偰傕抦傜傫乿偲尵偆栿偱偡丅亄俆倁偺扨堦揹尮偱巊梡偟偰偄傞応崌偼丄亄俆倁傪挻偊傞偙偲偼傕偪傠傫丄堦弖偱傕晧偺乮侽倁埲壓偺乯擖椡偑壛傢傟偽乽夡傟偰傕抦傜傫乿偲婰嵹偝傟偰偄傞栿偱偡偐傜丄扨堦揹尮偱偺擖椡偵偼拲堄偑昁梫側帠偑暘傝傑偡丅
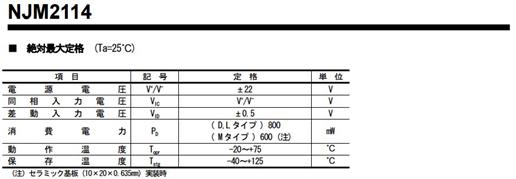
壓恾偺僐儞僷儗乕僞偼亅擖椡偵俀倁傪壛偊丄僗儗僢僔儑儖僪揹埑俀倁偲偟偰偄傑偡丅僐儞僷儗乕僞乕偺擖椡偲偟偰亄擖椡抂巕偵壛偊偨揹埑乮俁倁乯偲亅擖椡抂巕偺揹埑乮俀倁乯偵偼乮晧婣娨偺夞楬偲偼堎側傝乯揹埑偑乮侾倁乯惗偠偰偄傑偡丅偙偺傛偆偵丄亄擖椡偲亅擖椡偺娫偵壛偊傞揹埑偑嵎摦擖椡揹埑偱偡丅
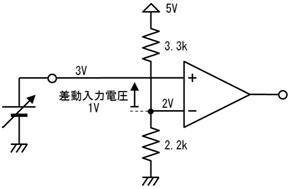
忋昞偵傛傟偽丄俶俰俵俀侾侾係偺嵎摦擖椡揹埑斖埻偺愨懳嵟戝掕奿偼嬐偐侽丏俆倁偱偡丅偮傑傝俶俰俵俀侾侾係偼忋恾偺夞楬偱偼巊梡偱偒傑偣傫丅乮帠幚忋僐儞僷儗乕僞偵偼巊梡偱偒傑偣傫乯偙傟偼俀侾侾係偑乮斈梡偱柍偔乯掅嶨壒偺僆乕僨傿僆愱梡僆儁傾儞僾偩偐傜偱偡丅
媡偵斈梡偺僆儁傾儞僾俶俰俵係俆俆俉偱偼丄亇侾俆倁揹尮偱巊梡偟偨偲偒偺嵎摦擖椡揹埑斖埻偺愨懳嵟戝掕奿偼亇俁侽倁偲側偭偰偍傝丄亄擖椡傪亄揹尮偵丄亅擖椡傪亅揹尮偵愙懕偟偰傕乮偦偺媡偱偁偭偰傕乯夡傟傑偣傫丅乮幚嵺偵偼乽崱偵傕夡傟偦偆乿乽杦偳夡傟傞乿偑惓夝偱偡乯
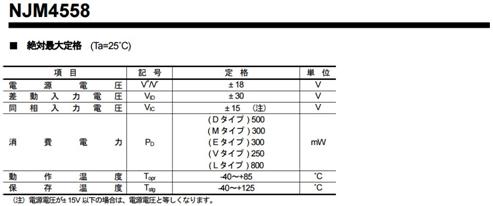
惓忢偵摦嶌偡傞偐斲偐偼揹婥揑摿惈偱妋擣偟傑偡丅壓昞偵帵偡偲偍傝丄係俆俆俉偺摨憡擖椡揹埑斖埻偼乮亇侾俆倁偺俀揹尮偺応崌乯昗弨偱亇侾係倁乮揹尮揹埑傛傝忋壓嫟偵侾倁彫偝偄斖埻乯丄塣偑埆偄偲乮嵟彫乯亇侾俀倁乮揹尮揹埑傛傝忋壓嫟偵俁倁彫偝偄斖埻乯偑摦嶌偡傞斖埻偱偡丅
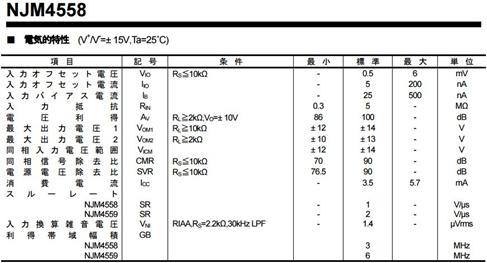
妟柺偳偍傝偵忋婰偺摨憡擖椡揹埑斖埻傪庴偗巭傔傞偲丄壓恾偱帵偡偲偍傝丄椺偊偽係俆俆俉傪俉倁扨堦揹尮偱巊梡偟偨応崌丄塣偑椙偗傟偽侾乣俈倁偺俇倁偺擖椡揹埑斖埻偱摦嶌偡傞傕偺偺丄塣偑埆偗傟偽俀乣俆倁偺俀倁偺擖椡揹埑斖埻偱偟偐惓忢摦嶌偟側偄偲傢偐傝傑偡丅乮壏搙傗慺巕偺屄懱嵎偵傛傞乯
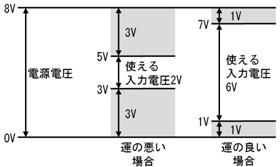
偝傜偵丄嵟弶偵偁偘偨僐儞僷儗乕僞夞楬偺傛偆偵丄俆倁扨堦揹尮偱偁傟偽丄塣偺埆偄応崌偵巊偊傞擖椡揹埑偺斖埻偑柍偔側偭偰偟傑偄傑偡偐傜乽係俆俆俉偼俆倁偱巊偊側偄乿偲側傝傑偡丅乮幚嵺偵偼壗偲偐摦偔応崌偑戝敿偱偡偑乧乯
侾俆. 棟憐偲尰幚偺堘偄係乮僗儖乕儗僀僩乯
壓恾嵍懁偺柍埨掕儅儖僠僶僀僽儗乕僞傪専摙偟偨偲偒丄壓恾塃懁偺僌儔僼偺傛偆偵丄僆儁傾儞僾偺弌椡偼乽堦弖偱斀揮偡傞乿偲峫偊傑偟偨丅
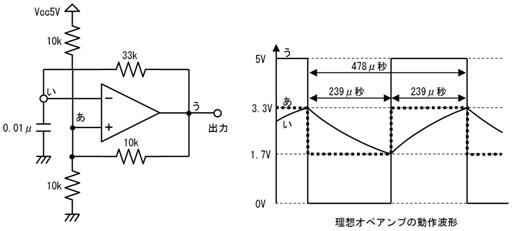
偲偙傠偑丄幚嵺偵忋恾偺夞楬傪嶌偭偰摦嶌偝偣傞偲丄堦弖偱偼斀揮偣偢丄帪娫偲偲傕偵弌椡偑曄壔偟偰峴偒傑偡丅壓恾忋抜偺幨恀偱偼暘偐傝擄偄応崌傕偁傝傑偡偑丄壓恾壓抜偺傛偆偵丄斀揮偡傞弖娫傪帪娫曽岦偵奼戝偡傞偲丄帪娫傪妡偗偰斀揮偡傞條巕偑偼偭偒傝暘傝傑偡丅壓恾壓抜偱偼丄墶侾栚惙傝偑侾侽兪昩偱偡丅
斀揮偵梫偡傞帪娫偼丄嘆偼係兪昩掱搙丄嘇偼偐側傝憗偔偰侾兪昩埲壓丄嘊偼俁侽兪昩掱搙梫偡傞忋丄搑拞偱堦夞媥宔偟偰偄傑偡丅
|
嘆儗僀儖僩僁儗僀儖僞僀僾
|
嘇斈梡僞僀僾
|
嘊斈梡扨揹尮僞僀僾
|
|

|

|

|
|
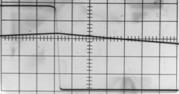
|
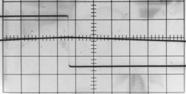
|

|
|
俴俵俠俇係俉俀
|
俶俰俵係俆俉侽
|
俴俵俁俆俉
|
偙偺傛偆偵乽弌椡偑斀揮偡傞憗偝乿傪乽侾兪昩偵壗倁曄壔偱偒傞偐乿偲偄偆広搙偱昞偟偨偺偑丄僗儖乕儗乕僩乮俽俼乯偲屇傇抣偱偡丅乮偙偺夞楬偺斀揮帪娫偼丄惓妋側僗儖乕儗乕僩偱偼側偔丄僎僀儞僶僀儞僪僂傿僘傕娭學偟偰偄傑偡乯偨偲偊偽丄忋偺俁偮偺僆儁傾儞僾偺僗儖乕儗乕僩偼丄壓昞偺傛偆偵寁嶼偡傞偙偲偑偱偒傑偡丅
|
|
俴俵俠俇係俉俀
|
俶俰俵係俆俉侽
|
俴俵俁俆俉
|
|
曄壔偵梫偡傞帪娫
|
係兪昩
|
侾兪昩
|
俁侽兪昩
|
|
曄壔偟偨揹埑
|
俆倁
|
俀丏俋倁
|
俀丏俋倁
|
|
僗儖乕儗乕僩
乮曄壔偺懍搙乯
|
俆倁乛係兪昩
亖侾丏俇倁乛兪昩
|
俀丏俋倁乛侾兪昩
亖俀丏俋倁乛兪昩
|
俀丏俋倁乛俁侽兪昩
亖侽丏侾倁乛兪昩
|
|
僨乕僞僔乕僩偺抣
|
侽丏俈倁乛兪昩
|
俆倁乛兪昩
|
侽丏俁倁乛兪昩
|
扐偟丄僨乕僞僔乕僩偺僗儖乕儗乕僩偼丄壓恾偺傛偆偵儐僯僥傿僎僀儞憹暆婍偵戝偒側怣崋傪擖傟偰應掕偡傞乮憹暆偝偣側偄偱應掕偡傞乯偒傑傝側偺偱丄僐儞僷儗乕僞偲偟偰棙梡偟偰偄傞帪偺抣傛傝丄戝偒側乮椙偄乯抣偑婰嵹偝傟偰偄傞応崌偑戝敿偱偡丅
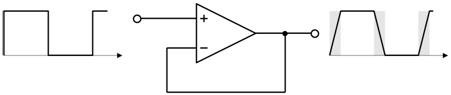
侾俇. 嶨壒
偙偙偱偼丄僆儁傾儞僾摍偺晹昳偑敪惗偝偣傞嶨壒傪愢柧偟傑偡丅憹暆棪偺崅偄憹暆婍偱偼丄怣崋傪擖傟偰偄側偄偲偒傕丄弌椡傪僀儎儂儞摍偱儌僯僞偡傟偽乽僓乕乿偲塉偺傛偆側壒偑暦偙偊傑偡丅偙傟偑晹昳偑弌偡嶨壒偱偡丅彫偝側怣崋傪憹暆偟偰棙梡偟偨偄応崌偵偼丄嶨壒傪彫偝偔偡傞岺晇偑昁梫偱偡丅
壓恾偵俁抜偺憹暆婍偺夞楬恾傪帵偟傑偡丅乽怣崋偺戝偒偝乿傪乽慄偺懢偝乿偱帵偟偰偄傑偡丅怣崋偑戝偒偗傟偽乮慄偑懢偗傟偽乯嶨壒偑崿擖偟偰傕柍帇偱偒傑偡偐傜丄嶨壒偵拲堄偡傞偺偼丄嵶偄慄偱帵偡彫偝側怣崋傪埖偆晹暘偱偡丅
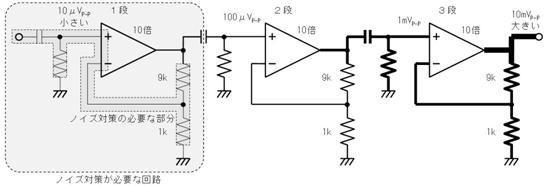
偨偲偊偽忋恾偺応崌偼丄嶰抜偺憹暆婍偺撪丄乮捠忢偼乯恾拞偱敄偄奃怓偵揾偭偨丄侾抜栚偵嶨壒懳嶔偑昁梫偱偡丅偝傜偵丄侾抜栚偺拞偱傕丄擹偄奃怓偵揾偭偨丄僆儁傾儞僾偺擖椡抂巕偲丄擖椡抂巕偵宷偑傞晹昳偑嶨壒偵塭嬁偟傑偡丅媡偵摨偠侾抜栚偱傕丄僆儁傾儞僾偺弌椡抂巕偱偼丄婛偵怣崋偑戝偒偔側偭偰偄傞偺偱丄嶨壒傊偺塭嬁偼杦偳偁傝傑偣傫丅
偱偡偐傜丄僆儁傾儞僾偺撪晹偱敪惗偡傞嶨壒傕乽擖椡抂巕偱敪惗偟偰偄傞乿偲峫偊傑偡丅僆儁傾儞僾偺擖椡抂巕偱偼丄嶨壒揹埑乮擖椡抂巕偵壛傢傞嶨壒偺揹埑乯偲嶨壒揹棳乮擖椡抂巕偵棳傟傞嶨壒偺揹棳乯偺俀庬椶偺嶨壒偑敪惗偟傑偡丅
嶨壒偵偮偄偰偺婰嵹偼僆儁傾儞僾偺昳庬偵傛傝條乆偱偡丅嶨壒惈擻傪廳帇偟偨僆儁傾儞僾偱偼徻偟偔丄偦偆偱側偄僆儁傾儞僾偱偼娙慺偵愢柧偝傟偰偄傑偡丅嶨壒傪慡偔婥偵偟側偄梡搑偺僆儁傾儞僾偱偼丄嶨壒惈擻偑婰嵹偝傟偰偄側偄応崌偝偊偁傝傑偡丅
僨乕僞僔乕僩偵搊応偡傞庡側嶨壒惈擻傪壓昞偵帵偟傑偡丅
|
暘椶
|
柤徧
|
扨埵
|
堄枴
|
|
嶨壒揹埑
|
嘆擖椡姺嶼嶨壒揹埑
Input voltage noize
|
VRMS
VP-P
|
偦偺僆儁傾儞僾偑庡偵棙梡偝傟傞廃攇悢偺斖埻偱丄擖椡偵敪惗偡傞嶨壒偺揹埑
|
|
嘇擖椡姺嶼嶨壒揹埑枾搙
Input voltage noize density
|
V/併Hz
|
侾俫倸偁偨傝偺嶨壒揹埑
|
|
嘊擖椡姺嶼嶨壒揹埑僗儁僋僩儔儉枾搙
Input Voltage Noise Spectral Density
|
Hz偲V/併Hz
僌儔僼
|
侾俫倸偁偨傝偺嶨壒揹埑偺廃攇悢偵傛傞曄壔偺條巕
|
|
嶨壒揹棳
|
嘋擖椡姺嶼嶨壒揹埑
Input current noize
|
ARMS
AP-P
|
偦偺僆儁傾儞僾偑庡偵棙梡偝傟傞廃攇悢偺斖埻偱丄擖椡偵敪惗偡傞嶨壒偺揹棳
|
|
嘍擖椡姺嶼嶨壒揹埑枾搙
Input current noize density
|
A/併Hz
|
侾俫倸偁偨傝偺嶨壒揹棳
|
|
嘐擖椡姺嶼嶨壒揹埑僗儁僋僩儔儉枾搙
Input currnet noize spectral density
|
Hz偲A/併Hz
僌儔僼
|
侾俫倸偁偨傝偺嶨壒揹棳偺廃攇悢偵傛傞曄壔偺條巕
|
嘆偲嘋偼娙曋側昞偟曽偱丄偨偲偊偽乽帹偱暦偙偊傞廃攇悢偺斖埻乿偲偄偭偨姶偠偱丄廃攇悢偺斖埻傪梊傔寛傔偰應掕偟偨嶨壒偺揹埑偱偡丅偦偺傑傑擖椡偵壛傢傞嶨壒偺戝偒偝乮揹埑傗揹棳乯偲偟偰棙梡偱偒傑偡丅偨偩偟丄巊梡偡傞廃攇悢偺斖埻偑應掕忦審偲堘偆応崌偼丄嶨壒偺戝偒偝偑惓妋偵暘傝傑偣傫丅
嘇偲嘍偼懡彮徻偟偄昞偟曽偱丄僨乕僞僔乕僩偺抣乮嶨壒枾搙乯偵丄帺暘偑巊梡偡傞廃攇悢偺斖埻乮傪儖乕僩偟偨抣傪乯妡偗偰丄嶨壒偺戝偒偝傪媮傔傑偡丅巊梡偡傞廃攇悢偺斖埻偑峀偄応崌偵丄偪傖傫偲嶨壒傕戝偒偔媮傔傞偙偲偑偱偒傑偡丅偨偩偟丄廃攇悢偵傛傞嶨壒偺戝偒偝偺曄壔偼暘傝傑偣傫丅
嘊偲嘐偼徻偟偄昞偟曽偱丄廃攇悢偵傛傞嶨壒偺戝偒偝偺曄壔傕娷傔偰丄帺暘偺巊梡偡傞廃攇悢偺斖埻偱偺嶨壒偺戝偒偝傪惓妋偵媮傔傞偙偲偑偱偒傑偡丅
嶨壒揹埑偼丄壓恾偵娵報偱帵偡乽嶨壒揹埑尮乿乮嶨壒揹埑傪敪惗偡傞晹昳乯偑丄擖椡抂巕偲捈楍偵擖偭偰偄傞偲峫偊偰夞楬傊偺塭嬁傪専摙偟傑偡丅偙偺偲偒丄壓恾偵帵偡傛偆偵乽亄擖椡偵擖偭偰偄傞乿偲峫偊偰傕乽亅擖椡偵擖偭偰偄傞乿偲峫偊偰傕摨偠寢壥偵側傝傑偡偐傜丄偳偪傜偱傕峫偊堈偄曽偵憓擖偟偰専摙偟傑偡丅
偙偺傛偆偵丄嶨壒揹埑傪僆僼僙僢僩揹埑偲帡偨曽朄偱峫偊偰椙偄偺偼丄嶨壒偑僆僼僙僢僩揹埑偺晄婯懃側曄壔偲傕尵偊傞偐傜偱偡丅
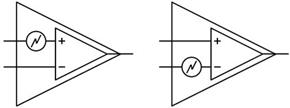
偙偺傛偆偵擖椡偱敪惗偟偰偄傞偲峫偊偨嶨壒揹埑傪乽擖椡姺嶼嶨壒揹埑乿偲屇傃丄偨偲偊偽乽擖椡姺嶼嶨壒揹埑侾兪倁俼俵俽乿偲帵偟傑偡丅
嶨壒揹埑偵巊傢傟偰偄傞扨埵丄幚岠抣揹埑乮倁俼俵俽乯偼丄岎棳揹埑乮倁俙俠乯偲杦偳摨偠堄枴偱偡丅偮傑傝丄幚岠抣揹埑侾倁俼俵俽偼乮岎棳揹埑侾倁俙俠偲摨條偵乯捈棳侾倁偲摨偠柧傞偝偱揹媴傪岝傜偣傞偙偲偑偱偒傞揹埑偱偡丅偨偩丄倁俙俠偼扨弮側怳摦傪孞傝曉偡岎棳傪昞偡偨傔偺扨埵側偺偱丄暋嶨偵曄壔偡傞嶨壒傪昞偡偺偵偼嵟揔偲偼尵偊偢丄乽捈棳侾倁偲摨偠埿椡偩偑丄攇宍偼晄柧側怣崋乿偲偄偆堄枴偺倁俼俵俽傪巊梡偟偰偄傑偡丅
偱偼丄擖椡姺嶼嶨壒揹埑偺塭嬁偱丄憹暆婍偺弌椡偵偳偺傛偆側嶨壒偑尰傟傞偐専摙偟傑偡丅壓恾偼侾侾攞偺旕斀揮憹暆夞楬偵丄擖椡姺嶼嶨壒揹埑侾兪倁俼俵俽偺僆儁傾儞僾傪巊偭偨椺偱偡丅
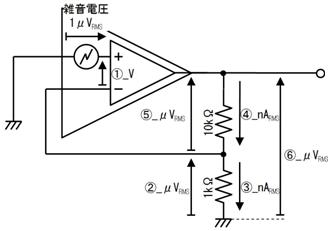
侾俋.侾. 楙廗
忋恾傪尒側偑傜丄壓昞偵彂偒崬傫偱弌椡偵尰傟傞嶨壒揹埑傪寁嶼偟傑偡丅
|
斣崋
|
幙栤
|
抣
|
|
|
亄擖椡抂巕偵壛傢傞嶨壒揹埑偼侾兪倁俼俵俽偱偡丅
|
乚
|
|
嘆
|
晧婣娨偺夞楬偺偨傔丄亄擖椡偲亅擖椡偼娫偺揹埑偼丄
|
倁
|
|
嘇
|
侾倠兌偺椉抂偺嶨壒揹埑偼丄
|
兪倁俼俵俽
|
|
嘊
|
侾倠兌偵棳傟傞嶨壒揹棳偼丄
|
値俙俼俵俽
|
|
嘋
|
侾侽倠兌偵棳傟傞嶨壒揹棳偼丄
|
値俙俼俵俽
|
|
嘍
|
侾侽倠兌偺椉抂偺嶨壒揹埑偼丄
|
兪倁俼俵俽
|
|
嘐
|
弌椡抂巕偺嶨壒揹埑偼丄
|
兪倁俼俵俽
|
侾俋.俀. 摎
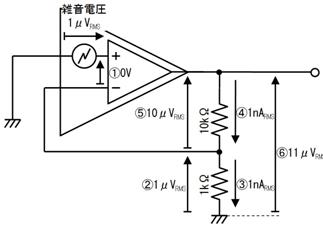
|
斣崋
|
幙栤
|
抣
|
|
|
亄擖椡抂巕偵壛傢傞嶨壒揹埑偼侾兪倁俼俵俽偱偡丅
|
乚
|
|
嘆
|
晧婣娨偺夞楬偺偨傔丄亄擖椡偲亅擖椡偼娫偺揹埑偼丄
|
侽倁
|
|
嘇
|
侾倠兌偺椉抂偺嶨壒揹埑偼丄
|
侾兪倁俼俵俽
|
|
嘊
|
侾倠兌偵棳傟傞嶨壒揹棳偼丄
|
侾値俙俼俵俽
|
|
嘋
|
侾侽倠兌偵棳傟傞嶨壒揹棳偼丄
|
侾値俙俼俵俽
|
|
嘍
|
侾侽倠兌偺椉抂偺嶨壒揹埑偼丄
|
侾侽兪倁俼俵俽
|
|
嘐
|
弌椡抂巕偺嶨壒揹埑偼丄
|
侾侾兪倁俼俵俽
|
偙偺傛偆偵憹暆夞楬偱偼丄擖椡姺嶼嶨壒揹埑偑乮奣偹乯憹暆棪偱奼戝偝傟偰弌椡偵尰傟傑偡丅
壓昞偼掅嶨壒僆儁傾儞僾俶俰俵俀侾俀俀偺揹婥揑摿惈偱偡丅
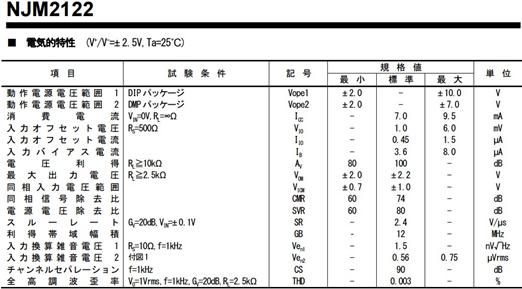
壓偐傜俁峴栚偵擖椡姺嶼嶨壒揹埑偺昗弨抣丄侽丏俆俇兪倁俼俵俽偑婰嵹偝傟偰偄傑偡丅
嶨壒揹棳偼丄嶨壒揹埑掱偼昿斏偵棙梡偟傑偣傫偑丄掞峈抣偺崅偄夞楬偱偼廳梫側応崌偑偁傝傑偡丅嶨壒揹棳偼丄壓恾偵娵報偱帵偡乽嶨壒揹棳尮乿乮嶨壒揹棳傪敪惗偡傞晹昳乯偑丄擖椡抂巕偲暲楍偵擖偭偰偄傞偲峫偊偰夞楬傊偺塭嬁傪専摙偟傑偡丅
偙偺傛偆偵擖椡偱敪惗偟偰偄傞偲峫偊偨嶨壒偺揹棳傪乽擖椡姺嶼嶨壒揹棳乿偲屇傃丄偨偲偊偽乽擖椡姺嶼嶨壒揹棳侾侽倫俙俼俵俽乿偲帵偟傑偡丅
偱偼丄擖椡姺嶼嶨壒揹棳偺塭嬁偱丄憹暆婍偺弌椡偵偳偺傛偆側嶨壒偑敪惗偡傞偐専摙偟傑偡丅壓恾偼侾侾攞偺旕斀揮憹暆夞楬偵丄擖椡姺嶼嶨壒揹棳侾侽倫俙俼俵俽偺僆儁傾儞僾傪巊偭偨椺偱偡丅
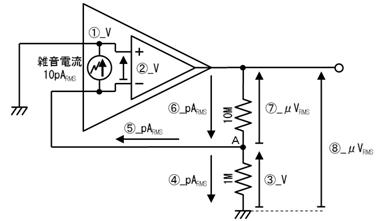
俀侽.侾. 楙廗
忋恾傪尒側偑傜丄壓昞偵彂偒崬傫偱弌椡偵尰傟傞嶨壒揹埑傪寁嶼偟傑偡丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄
乮傾乕僗偵愙懕偝傟偰偄傞偐傜乯
|
倁
|
|
嘇
|
晧婣娨偺夞楬偩偐傜丄亄擖椡偲亅擖椡偺揹埑嵎偼丄
|
倁
|
|
嘊
|
侾俵兌偺椉抂揹埑偼丄
|
倁
|
|
嘋
|
侾俵兌偵棳傟傞揹棳偼丄
|
倫俙俼俵俽
|
|
嘍
|
嶨壒揹棳偑侾侽倫俙偩偐傜丄婣娨夞楬偵棳傟傞嶨壒揹棳偼丄
|
倫俙俼俵俽
|
|
嘐
|
侾侽俵兌偵棳傟傞揹棳偼丄
|
倫俙俼俵俽
|
|
嘑
|
侾侽俵兌偺椉抂揹埑偼丄
|
兪倁俼俵俽
|
|
嘒
|
弌椡偝傟傞嶨壒揹埑偼丄
|
兪倁俼俵俽
|
俀侽.俀. 摎
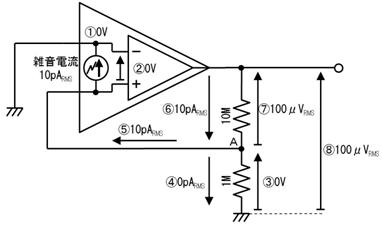
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
亄擖椡偺揹埑偼丄
乮傾乕僗偵愙懕偝傟偰偄傞偐傜乯
|
侽倁
|
|
嘇
|
晧婣娨偺夞楬偩偐傜丄亄擖椡偲亅擖椡偺揹埑嵎偼丄
|
侽倁
|
|
嘊
|
侾俵兌偺椉抂揹埑偼丄
|
侽倁
|
|
嘋
|
侾俵兌偵棳傟傞揹棳偼丄
|
侽倫俙俼俵俽
|
|
嘍
|
嶨壒揹棳偑侾侽倫俙偩偐傜丄婣娨夞楬偵棳傟傞揹棳偼丄
|
侾侽倫俙俼俵俽
|
|
嘐
|
侾侽俵兌偵棳傟傞揹棳偼丄
|
侾侽倫俙俼俵俽
|
|
嘑
|
侾侽俵兌偺椉抂揹埑偼丄
|
侾侽侽兪倁俼俵俽
|
|
嘒
|
弌椡偝傟傞嶨壒揹埑偼丄
|
侾侽侽兪倁俼俵俽
|
偮傑傝偙偺夞楬偱偼丄僆儁傾儞僾偺嶨壒揹棳偑侾侽俵兌偵棳傟偰惗偠傞揹埑偑丄憹暆婍偺弌椡嶨壒揹埑偵側傝傑偡丅偙偺傛偆偵丄抣偺戝偒偄掞峈傪巊梡偟偨夞楬偱嶨壒揹棳偑栤戣偵側傝傑偡丅
嶨壒偼條乆側廃攇悢偺怣崋偑棎嶨偵擖傝崿偠偭偨傕偺偱偡丅嶨壒偺嫮偝偼廃攇悢偵傛偭偰曄壔偟丄偦偺曄壔偺條巕傕僆儁傾儞僾偺昳庬偵傛偭偰堘偄傑偡丅偱偡偐傜丄帺暘偑巊梡偡傞廃攇悢偺斖埻偱嶨壒偑彮側偄僆儁傾儞僾傪慖傇昁梫偑偁傝傑偡丅
偙偺偨傔偵乮嶨壒惈擻傪廳帇偟偨僆儁傾儞僾偺乯僨乕僞僔乕僩偵偼丄墶幉傪廃攇悢丄廲幉傪嶨壒偺戝偒偝丄偲偟偰昤偄偨僌儔僼偑宖嵹偝傟偰偄傑偡丅僀儊乕僕揑偵偼嶨壒偺廃攇悢摿惈偺傛偆側傕偺偱偡丅
偙偺僌儔僼偺惓幃柤徧偼乽擖椡姺嶼嶨壒揹埑僗儁僋僩儔儉枾搙 懳 廃攇悢乿input reffered noize voltage spectral density vs frequency偲偄偆挿偄柤慜偱偡偑丄僨乕僞僔乕僩偵偼乽擖椡姺嶼嶨壒揹埑乿摍偲揔摉偵柤慜傪抁弅偟偰宖嵹偝傟偰偄傑偡丅
壓恾偼丄俴俵俉俁俁偺擖椡姺嶼嶨壒揹埑僗儁僋僩儔儉枾搙乮嵍懁乯偲擖椡姺嶼嶨壒揹棳僗儁僋僩儔儉枾搙乮塃懁乯偺僌儔僼偱偡丅乮偙偺僨乕僞僔乕僩偱傕柤慜偼抁弅偝傟偰偄傑偡乯
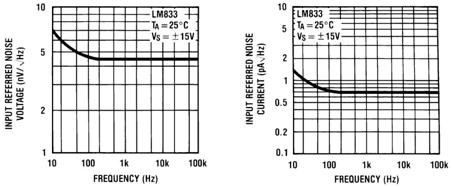
奺廃攇悢偱偺嶨壒偺戝偒偝偼丄nV/併Hz傗丄pA/併Hz偲偄偭偨晽曄傢傝側扨埵偱昞帵偝傟傑偡丅忋恾偵傛傟偽丄揹埑嶨壒傕揹棳嶨壒傕丄崅偄廃攇悢偱偼廃攇悢偵傛傜偢堦掕偱偡偑丄侾侽侽俫倸埲壓偺廃攇悢偱偼憹壛偡傞偙偲偑傢偐傝傑偡丅懡偔偺僆儁傾儞僾偑偙偺傛偆側孹岦傪帩偭偰偄傑偡丅
偝偰丄僌儔僼偑暯傜偵側偭偰偄傞斖埻偺廃攇悢傪棙梡偡傞応崌偼丄娙扨側寁嶼偱擖椡嶨壒揹埑傪媮傔傞偙偲偑偱偒傑偡丅偨偲偊偽丄侾侽侽俫倸乣侾侽俲俫倸偺怣崋傪棙梡偡傞応崌丄忋恾嵍偺僌儔僼偐傜丄揹埑嶨壒偑係丏俆値倁乛併俫倸掱搙偱堦掕偲撉傒庢傟傑偡偐傜丄師偺傛偆偵擖椡姺嶼嶨壒揹埑傪寁嶼偟傑偡丅
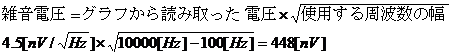
=4.5E-9*SQRT(10E3-100)
廃攇悢偺暆偵併傪晅偗傞偺偼丄乽嶨壒偼揹椡偱懌偟嶼偡傞乿昁梫偑偁傞偐傜偱偡丅嶨壒偺懌偟嶼偵偮偄偰偼丄暿搑愢柧偟傑偡丅傑偨丄僌儔僼偑暯傜偱柍偄廃攇悢偺斖埻偵偮偄偰傕丄暿搑愢柧偟傑偡丅
壓恾偼揟宆揑側僆儁傾儞僾偺嶨壒僗儁僋僩儔儉枾搙偺椺偱偡丅嶨壒偵偼乽偳偺傛偆側廃攇悢偵傕枮曊側偔暘晍偡傞乿儂儚僀僩嶨壒乮悈暯側揰慄乯偲丄乽掅偄廃攇悢偱戝偒偔側傞乿僺儞僋嶨壒乮幬傔偺揰慄乯偑偁傝傑偡丅偦傟偧傟暿偺尨場偱敪惗偟偰偄傞嶨壒偱偡丅
儂儚僀僩嶨壒偼僔儑僢僩嶨壒丄僺儞僋嶨壒偼侾乛倖乮僄僼僽儞僲僀僠嶨壒乯丄僼儕僢僇嶨壒偲傕屇偽傟傑偡丅
僺儞僋嶨壒偼丄廃攇悢偑侾侽侽暘偺侾偵側傞偲丄怳暆偑侾侽攞偵戝偒偔側傝傑偡丅嶲峫偺偨傔偵壓恾偵嵶慄偱帵偟偨俠俼僼傿儖僞乮愊暘夞楬乯偺摿惈偱偼丄廃攇悢偑侾侽暘偺侾偵側傞偲丄怳暆偑侾侽攞偵戝偒偔側傝傑偡丅偱偡偐傜丄僺儞僋嶨壒偺憹壛偺惃偄偼丄俠俼夞楬傛傝壐傗偐偱偡丅
捠忢偺僆儁傾儞僾偱偼丄恾偵奃怓偺懢慄偱帵偡傛偆偵丄僺儞僋嶨壒偲儂儚僀僩嶨壒偺崌寁偑丄嶨壒偲偟偰尰傟傑偡丅
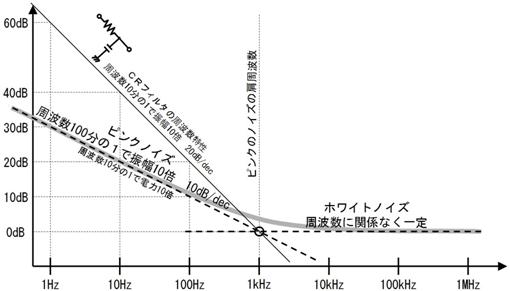
暯傜側儂儚僀僩嶨壒偺揰慄偲丄幬傔偺僺儞僋嶨壒偺揰慄偑岎傢傞廃攇悢傪丄僺儞僋嶨壒偺尐廃攇悢偲屇傃傑偡丅儂儚僀僩嶨壒偺戝偒偝偑摨偠側傜丄僺儞僋嶨壒偺尐廃攇悢偑掅偗傟偽掅偄傎偳丄僺儞僋嶨壒偑彫偝偄偙偲傪帵偟傑偡丅
僺儞僋嶨壒偺尐廃攇悢偼丄僺儞僋嶨壒偺愙慄廃攇悢丄僺儞僋嶨壒偺僐乕僫乕丄僺儞僋嶨壒僞儞僕僃儞僩偲丄條乆側柤慜偱屇偽傟傑偡丅
壏搙僙儞僒乕偺傛偆側嬌傔偰廃攇悢偺掅偄乮捈棳偵嬤偄乯怣崋傪埖偆応崌偵偼丄僺儞僋偺嶨壒偑栤戣偵側傝傑偡丅偙偺傛偆側応崌偼丄僺儞僋嶨壒偺彫偝側僆儁傾儞僾傪丄偮傑傝丄僺儞僋嶨壒偺尐廃攇悢偺掅偄僆儁傾儞僾傪慖傃傑偡丅
壓恾乮倎乯偺傛偆偵丄侾倁俙俠偺岎棳偲侾倁俙俠偺岎棳傪壛偊傞偲丄俀倁俙俠偺岎棳偵側傝傑偡丅
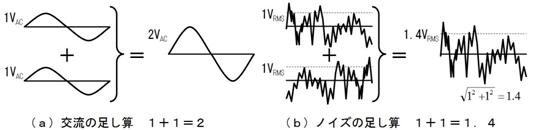
偲偙傠偑嶨壒偺応崌丄忋恾乮倐乯偺傛偆偵丄侾倁俼俵俽偺嶨壒偲丄侾倁俼俵俽偺嶨壒傪壛偊傞偲丄侾丏係倁俼俵俽偵側傝傑偡丅偙傟偼丄岎棳偑偍屳偄偵懅傪崌傢偣偰攇懪偭偰偄傞乮僐僸乕儗儞僩側乯偺偵懳偟偰丄嶨壒偑晄懙偄偵曄壔偟偰偄傞乮僀儞僐僸乕儗儞僩側乯偨傔偱偡丅偙偺傛偆側尰徾偼嶨壒埲奜偱傕惗偠傑偡丅偨偲偊偽俙偝傫偺惡侾倁俼俵俽偲俛偝傫惡侾倁俼俵俽傪壛偊偰傕丄侾丏係倁俼俵俽偵偟偐側傝傑偣傫丅俙偝傫惡偺攇宍偲丄俛偝傫偺惡偺攇宍偑乮壒怓偼帡偰偄偰傕乯堘偆宍偩偐傜偱偡丅
偱偼丄嶨壒揹埑傪懌偟嶼偡傞曽朄傪峫偊傑偡丅偨偲偊嶨壒偺傛偆偵晄懙偄側怣崋偱傕丄僄僱儖僊乕偼曐懚偝傟傑偡丅偮傑傝揹椡偑侾倂偺嶨壒偲俀倂偺嶨壒傪壛偊傞偲丄俁倂偺嶨壒偲側傝傑偡丅偦偙偱丄揹椡偵拲栚偟偰揹埑偺懌偟嶼傪峫偊傑偡丅
壓恾嵍懁偵丄俁倁俼俵俽偲係倁俼俵俽偺嶨壒偵傛偭偰丄侾兌偺掞峈偵敪惗偡傞揹椡傪帵偟傑偡丅俁倁俼俵俽側傜俁俙俼俵俽偺揹棳偑棳傟偰俋倂偺揹椡偑惗偠丄係倁俼俵俽側傜侾俇倂偺揹椡偑惗偠傑偡丅偮傑傝丄崌寁俀俆倂偺揹椡偑惗偠傑偡丅
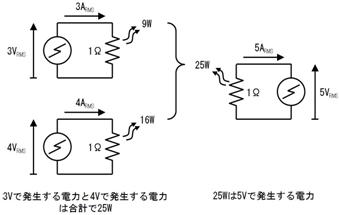
忋恾塃懁偱偼丄摨偠侾兌偺掞峈偵俀俆倂偺揹椡偑惗偠傞條巕傪帵偟傑偡丅揹埑偑俆倁俼俵俽偺偲偒丄俆俙俼俵俽偺揹棳偑棳傟傞寢壥丄俀俆倂偑惗偠傑偡丅
偮傑傝丄揹椡偵拲栚偡傞偲丄俁倁俼俵俽乮俋倂乯偲係倁俼俵俽乮侾俇倂乯傪壛偊傞偲崌寁俆倁俼俵俽乮俀俆倂乯偲側傝傑偡丅偙偺峫偊曽傪巊偆偲丄俙
[倁俼俵俽]偲俛 [倁俼俵俽]偺俀偮偺嶨壒偺懌偟嶼偺曽朄偼丄
俙偱惗偠傞揹椡亖俙俀 乮俙 [倁俼俵俽]偱丄俙 [俙俼俵俽]偩偐傜乯
俛偱惗偠傞揹椡亖俛俀 乮俛 [倁俼俵俽]偱丄俛 [俙俼俵俽]偩偐傜乯
崌寁偺揹椡亖俙俀亄俛俀
崌寁偺揹椡傪敪惗偝偣傞揹埑亖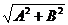
偲丄嶨壒偺崌寁偼乽擇忔偟偰偐傜崌寁偟偰丄崌寁偟偰偐傜儖乕僩傪庢傞乿偙偲偱寁嶼偱偒傑偡丅
僆儁傾儞僾偺嶨壒僗儁僋僩儔儉枾搙偲丄憹暆婍偺摿惈偑暘傟偽丄恾偺忋偱懌偟崌傢偣傞偩偗偱丄憹暆婍偺弌椡偺嶨壒僗儁僋僩儔儉枾搙傪媮傔傞偙偲偑偱偒傑偡丅
壓恾偵侾倠俫倸偱懷堟惂尷偟偨侾侽攞偺斀揮憹暆夞楬偲偦偺廃攇悢摿惈傪帵偟傑偡丅
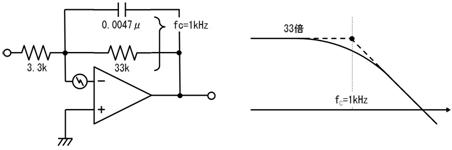
忋恾偺夞楬偵丄壓恾偵揰慄偱帵偡擖椡姺嶼嶨壒揹埑乮惓偟偔偼丄擖椡姺嶼嶨壒揹埑僗儁僋僩儔儉枾搙乯偺僆儁傾儞僾傪巊梡偟偨応崌丄憹暆婍偺弌椡嶨壒揹埑偼丄壓恾偵懢慄偱帵偡摿惈偲側傝傑偡丅
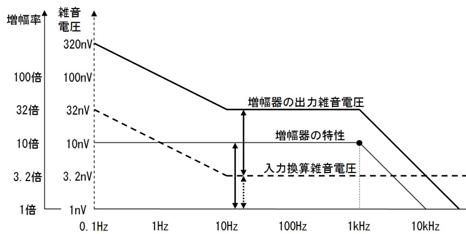
擖椡姺嶼嶨壒揹埑偑憹暆棪偺暘戝偒偔側傝傑偡偐傜丄侾倠俫倸埲壓偺斖埻偱偼擖椡姺嶼嶨壒揹埑偼侾侽攞偝傟偰弌椡偵尰傟傑偡丅乮忋偵僔僼僩偟傑偡乯丅傑偨丄侾倠俫倸埲忋偺斖埻偱偼丄憹暆棪偑乽廃攇悢侾侽攞偱怳暆侾侽暘偺侾乿偺惃偄偱掅壓偟偰峴偔偨傔丄擖椡偵壛傢傞嶨壒偺戝偒偝偼曄壔偟傑偣傫偑丄憹暆婍偺弌椡偵偁傜傢傟傞嶨壒偼乽廃攇悢侾侽攞偱怳暆侾侽暘偺侾乿偺惃偄偱掅壓偟傑偡丅
憹暆棪侾攞傪嵟掅抣乮堦斣壓乯偵偟偰懳悢僌儔僼傪昤偔偲丄擖椡姺嶼嶨壒揹埑偲憹暆婍偺摿惈偺崅偝傪壛偊傞偩偗偱丄憹暆婍偺弌椡嶨壒揹埑傪媮傔傞偙偲偑偱偒傑偡丅
夞楬偺弌椡怣崋偺嶨壒僗儁僋僩儔儉枾搙偐傜丄偦偺夞楬偼偳偺廃攇悢偱偺嶨壒偑戝偒偄偐丄娙扨偵抦傞偙偲偑偱偒傑偡丅
壓恾偵揰慄偱帵偡傛偆偵乮廃攇悢偑侾侽侽攞偵側傞偲嶨壒揹埑偑侾侽暘偺侾偵尭彮偡傞孹偒偺乯幬慄傪丄嶨壒摿惈偲愙偡傞傛偆偵昤偒傑偡丅嶨壒摿惈偲幬慄偑愙偡傞晅嬤偑丄嶨壒偺戝偒偄廃攇悢偱偡丅壓恾偺応崌丄崟娵偺晹暘偱愙偡傞偨傔丄侾倠俫倸廃曈偺奃怓偵揾偭偨晹暘偱嶨壒偑懡偄偙偲偑暘傝傑偡丅偱偡偐傜丄偙偺偁偨傝偺嶨壒偼怲廳偵寁嶼偡傞昁梫偑偁傞偲暘傝傑偡丅
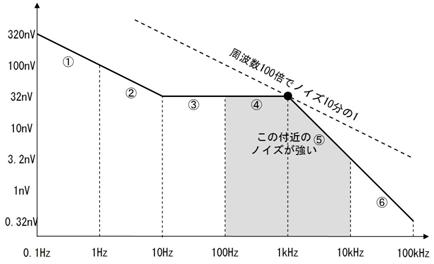
偱偼丄偙偺夞楬偺嶨壒弌椡揹埑傪寁嶼偟傑偡丅嶨壒偼丄侾俫倸丄侾侽俫倸丄侾侽侽俫倸偲侾侽攞嬫愗傝偵寁嶼偡傞偲妝偱偡偐傜丄嵟弶偵丄忋恾偺嘆乣嘐偺傛偆偵嬫娫傪愝偗傑偡丅嬫娫偼僌儔僼偺孹幬偵傛偭偰師偺傛偆偵暘椶偱偒傑偡丅
|
嬫娫
|
孹幬偺摿挜
|
嬫娫偺摿挜
|
妡偗傞抣
|
|
嘆偲嘇
|
廃攇悢偑侾侽侽攞偵側傞偲嶨壒揹埑偑侾侽暘偺侾偵尭傞
|
僺儞僋嶨壒偺嬫娫
|
俀丏係
|
|
嘊偲嘋
|
廃攇悢偵娭學側偔丄嶨壒揹埑偑堦掕
|
儂儚僀僩嶨壒偺嬫娫
|
侽丏俋俆
|
|
嘍偲嘐
|
廃攇悢偑侾侽攞偵側傞偲嶨壒偑侾侽暘偺侾偵尭傞
|
憹暆夞楬偑愊暘摦嶌
偟偰偄傞嬫娫
|
侾丏俆
|
忋昞偺乽妡偗傞悢乿偼屻偱愢柧偡傞奺嬫娫偺嶨壒揹埑偺寁嶼偱棙梡偟傑偡丅
幚嵺偺夞楬偱偼丄嶨壒摿惈偺愜傟嬋偑傝揰偑丄偪傚偆偳嬫娫偺愗傟栚偵棃傞偙偲偼偁傝傑偣傫丅嶨壒偼慺巕偵傛傞屄懱嵎偑戝偒偔丄惓妋偵寁嶼偡傞堄枴偼偦傟掱偁傝傑偣傫偐傜丄侾侽攞嬫愗傝偵崌偆傛偆偵丄嶨壒摿惈傪懡彮廋惓偟偰寁嶼偟傑偡丅
儂儚僀僩嶨壒偺嬫娫偼丄壓恾偵帵偡傛偆偵廃攇悢偵娭學側偔嶨壒揹埑偑堦掕偵側傝傑偡丅偙偺傛偆側応崌丄侾嬫娫偁偨傝偺嶨壒揹埑偼丄
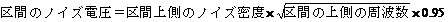
偱寁嶼偱偒傑偡丅壓恾偺椺偱偼丄=32E-9*SQRT(1000)*0.95偲寁嶼偟偰丄961nV偲暘傝傑偡丅
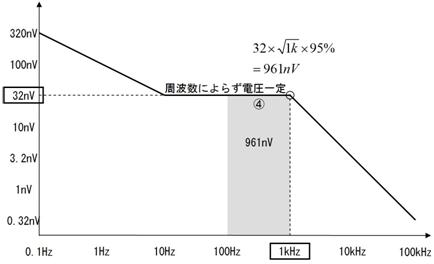
僺儞僋嶨壒偺嬫娫偼丄壓恾偵帵偡傛偆偵廃攇悢偑侾侽侽攞偵側傞偲丄嶨壒揹埑偑侾侽暘偺侾偵尭彮偟傑偡丅乮俁倓俛乛倧們倲丄侾侽倓俛乛倓倕們乯偙偺傛偆側応崌丄侾嬫娫偁偨傝偺嶨壒揹埑偼丄
偱寁嶼偱偒傑偡丅壓恾偺椺偱偼丄=32E-9*SQRT(10)*1.5偲寁嶼偟偰丄152nV偲暘傝傑偡丅
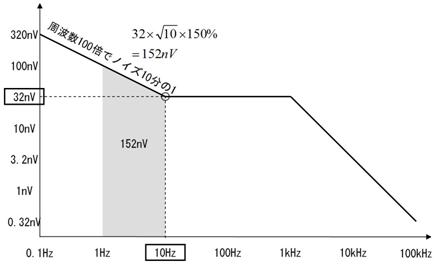
憹暆夞楬偑愊暘摦嶌偟偰偄傞嬫娫偼丄壓恾偵帵偡傛偆偵廃攇悢偑侾侽攞偵側傞偲丄嶨壒揹埑偑侾侽暘偺侾偵尭彮偟傑偡丅乮俇倓俛乛倧們倲丄俀侽倓俛乛倓倕們乯偙偺傛偆側応崌丄侾嬫娫偁偨傝偺嶨壒揹埑偼丄
偱寁嶼偱偒傑偡丅壓恾偺椺偱偼丄=32E-9*SQRT(10E3)*2.4偲寁嶼偟偰丄768nV偲暘傝傑偡丅
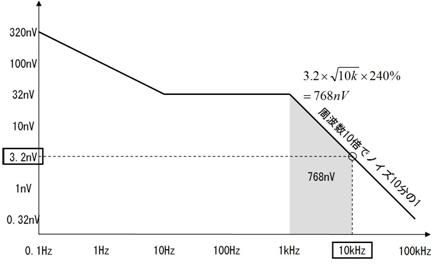
偙偺傛偆偵偟偰媮傔偨奺嬫娫偺嶨壒揹埑傪壓恾偵帵偟傑偡丅
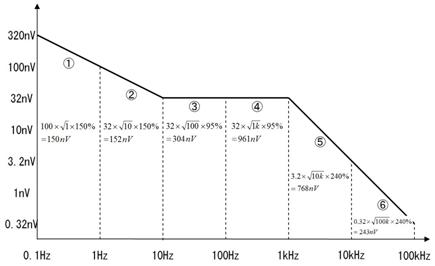
嘆乣嘐偺嬫娫偦傟偧傟偺嶨壒揹埑偼壓昞偺俤倶們倕倢僔乕僩偱媮傔傞偙偲偑偱偒傑偡丅

僔乕僩偺俤楍偵奺嬫娫偺嶨壒揹埑偑昞帵偝傟傑偡丅慡偰偺嬫娫偺嶨壒揹埑偺崌寁偼乽嶨壒偺懌偟嶼乿偱愢柧偟偨傛偆偵乽擇忔偟偰偐傜崌寁偟偰丄崌寁偟偰偐傜儖乕僩傪庢傞乿曽朄偱寁嶼偟傑偡丅俥楍偱奺嬫娫偺嶨壒揹埑傪俀忔偟丄俧楍偵偦偺崌寁傪丄俫楍偵崌寁傪儖乕僩偟偨抣傪昞帵偟偰偄傑偡丅
忋偺僔乕僩傪寁嶼偡傞偲丄壓昞偺傛偆偵側傝傑偡丅
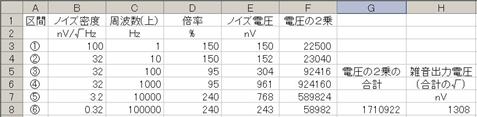
慡嬫娫偺嶨壒揹埑偺崌寁偼丄侾俁侽俉値倁乮侾丏俁兪倁乯偲暘傝傑偡丅奺嬫娫偺嶨壒揹埑傪壓恾偵帵偟傑偡丅
掞峈傕嶨壒傪敪惗偟傑偡丅嶨壒枾搙偼偳偺廃攇悢偱傕堦掕偱丄巊梡偡傞廃攇悢偺斖埻偲掞峈抣偐傜丄嶨壒揹埑偲嶨壒揹埑枾搙偼師偺傛偆偵寁嶼偱偒傑偡丅
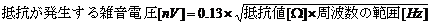
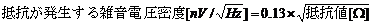
偨偲偊偽丄侾侽俵兌偺掞峈偼俀侽乣俀侽倠俫倸偺廃攇悢偺斖埻偱偼丄
=0.13*SQRT(10E6*(20E3-20))
[nV]
=0.13*SQRT(10E6) [nV/併Hz]
偲擖椡偟偰丄嶨壒揹埑俆俉侽侽侽値倁乮俆俉兪倁乯丄嶨壒揹埑枾搙係侾侽値倁偲寁嶼偱偒傑偡丅
傑偨丄掞峈偑敪惗偡傞嶨壒揹棳偲嶨壒揹棳枾搙偼丄
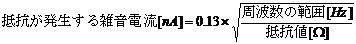
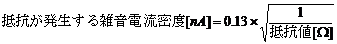
偨偲偊偽丄侾侽俵兌偺掞峈偼俀侽乣俀侽倠俫倸偺廃攇悢偺斖埻偱偼丄
=0.13*SQRT((20E3-20)/10E6)
[nV]
=0.13*SQRT(1/10E6) [nA/併Hz]
偲擖椡偟偰丄嶨壒揹棳侽丏侽侽俆俉値俙乮俆丏俉倫俙乯丄嶨壒揹棳枾搙侽丏侽係侾倫俙乛併俫倸偲寁嶼偱偒傑偡丅
壓昞偵奺庬偺掞峈偱敪惗偡傞嶨壒偺堦棗傪帵偟傑偡丅掞峈偺嶨壒偑巊梡偡傞僆儁傾儞僾偺擖椡嶨壒傛傝侾寘埲忋彫偝偗傟偽丄婥偵偡傞昁梫偼偁傝傑偣傫丅
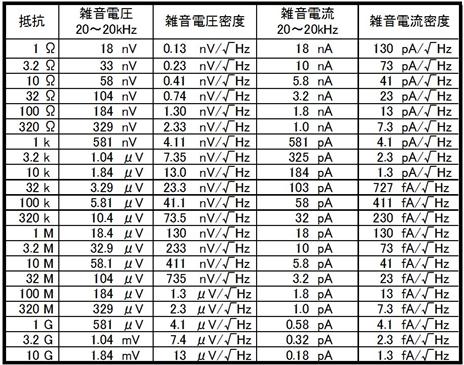
掞峈偺嶨壒偑僆儁傾儞僾偺擖椡嶨壒偵嬤偄丄偁傞偄偼戝偒偄応崌偼丄掞峈抣傪彫偝偔偱偒側偄偐丄懷堟傪嫹偔偱偒側偄偐傪専摙偟傑偡丅
徻嵶偼偲傕偐偔丄偲傝偁偊偢丄偩偄偨偄偺僀儊乕僕傪攃埇偡傞偙偲偑棟夝偺憗摴偱偡丅偙偙偱偼丄敿摫懱偺摥偒偲墳梡夞楬偺戝嶨攃側暤埻婥傪愢柧偟傑偡丅
敿摫懱慺巕偺愢柧偵愭棫偭偰丄乽敿摫懱暔惈乿偺愢柧傪峴偆偺偑悽娫偺偍栺懇偱偡丅偟偐偟丄尰幚偵偼乽敿摫懱偺拞偱壗偑婲偙偭偰偄傞偺偐乿傪抦傜側偔偰傕僟僀僆乕僪傗僩儔儞僕僗僞偼巊偊傑偡丅媡偵乽敿摫懱偺拞偱婲偙偭偰偄傞帠乿傪惓妋偵愢柧偟傛偆偲偡傞偲乮恄偼偳偺傛偆偵悽奅傪愝寁偟偨偐偲偄偆榖偵側傝乯榖偑嬌傔偰挿偔側傝傑偡丅偦偙偱杮彂偱偼丄敿摫懱偺惈幙偲僟僀僆乕僪傗僩儔儞僕僗僞偺摦嶌傪丄埨堈側偨偲偊榖偱庤抁偵愢柧偟傑偡丅

忋恾乮倎乯偵帵偡傛偆偵丄摵側偳偺摫懱乮揹婥傪椙偔棳偡暔幙乯偵偼丄朙晉偵堏摦壜擻側揹巕乮崟娵乯偑懚嵼偟乮揹巕偑堏摦偟偰揹棳傪塣傇偺偱乯揹棳偑椙偔棳傟傑偡丅偲偙傠偑丄忋恾乮倐乯偵帵偡傛偆偵丄僈儔僗摍偺愨墢懱乮揹婥傪棳偝側偄暔幙乯偱偼丄揹巕偑怺偄寠偺掙偵屌掕偝傟偰偄偰丄堏摦偡傞偙偲偑偱偒偢丄揹棳偑棳傟傑偣傫丅
偝偰丄俶宆敿摫懱偼忋恾乮們乯偺傛偆偵丄彮偟偩偗堏摦壜擻側揹巕偑偁傞暔幙偱丄俹宆敿摫懱偼忋恾乮倓乯偺傛偆偵丄揹巕偑弌擖傝偱偒傞愺偄寠偺偁傞暔幙偱偡丅
俶宆敿摫懱偱偼丄壓恾乮倎乯偺傛偆偵丄揹巕偑堏摦偟偰揹棳偑棳傟傑偡丅偙偺傛偆偵丄揹巕偑揹婥傪塣傫偱偄傞傛偆偵尒偊傞偺偱丄俶宆敿摫懱偱偼揹巕傪乽僉儍儕傾乿乮塣傃壆乯偲屇傃傑偡丅傑偨丄俹宆敿摫懱偼丄壓恾乮倐乯偺傛偆偵丄強乆偵愺偄寠偑偁傞偺偱丄揹巕偑寠揱偄偵搉傝曕偄偰揹棳偑棳傟傑偡丅
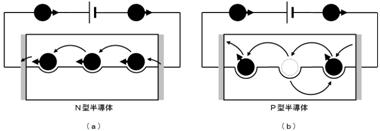
尒曽傪曄偊傞偲丄俹宆敿摫懱偱偼揹巕偑堏摦偡傞曽岦偲偼媡岦偒偵乮嬻偺乯寠偑堏摦偟偰偄傞傛偆偵尒偊傑偡丅偦偙偱丄俹宆敿摫懱偱偼嬻偺寠乮儂乕儖乯傪乽僉儍儕傾乿偲屇傃傑偡丅
側傫傜偐偺棟桼偱丄俶宆敿摫懱偺揹巕偑偳偙偐傊峴偭偰偟傑偆偲乮壓恾乮倎乯乯僉儍儕傾乮揹巕乯偑側偔側偭偰愨墢惈偲側傝丄揹棳偑棳傟側偔側傝傑偡丅摨條偵丄俹宆敿摫懱偺儂乕儖偑揹巕偱杽傑偭偰偟傑偆偲乮壓恾乮倐乯乯僉儍儕傾乮嬻偺寠乯偑柍偔側偭偰愨墢惈偲側傝丄揹棳偑棳傟側偔側傝傑偡丅
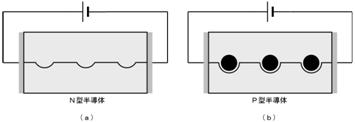
俶宆敿摫懱偲俹宆敿摫懱傪傄偭偨傝偔偭偮偗傞偙偲傪乽俹俶愙崌乿偲屇傃傑偡丅偔偭偮偗偨柺乮愙崌柺乯偱偼丄壓恾拞墰晹偵帵偡傛偆偵丄俶宆敿摫懱偺揹巕偑俹宆敿摫懱偺儂乕儖偵堏摦偟偰寢崌偟丄奃怓偱帵偡愨墢惈偺憌偑偱偒傑偡丅偙偺憌傪嬻朢憌乮僉儍儕傾偺柍偄摫揹惈偺朢偟偄憌乯偲屇傃傑偡丅
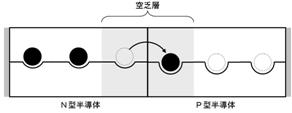
偙偺俹俶愙崌偺丄俶宆懁偵亄偺丄俹宆懁偵亅偺揹埑傪妡偗傞偲丄壓恾偵帵偡偲偍傝丄俶宆偺懁偱偼乮嵍抂偺亄揹埑偵堷偐傟偰乯揹巕偑扗傢傟偰丄俹宆偺懁偱偼寠偑乮塃懁偐傜擖傝崬傫偩乯揹巕偱杽傔傜傟偰丄愨墢惈偺嬻朢憌偑峀偑傞偽偐傝偱丄揹棳偑棳傟傑偣傫丅
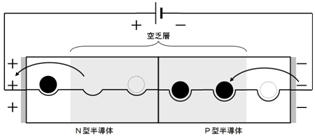
媡偵丄俶宆懁偵亅偺丄俹宆懁偵亄偺揹埑傪妡偗傞偲丄壓恾偵帵偡偲偍傝丄俶宆偺懁偱偼乮嵍懁偐傜乯揹巕偑嫙媼偝傟丄俹宆偺懁偱偼寠偐傜乮塃懁傊乯揹巕偑庢傝彍偐傟偰丄嬻朢憌偑徚幐偟丄揹棳偑棳傟傑偡丅
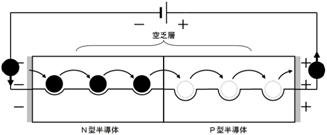
偙偺傛偆偵堦曽岦偵偩偗揹棳傪棳偡嶌梡傪乽惍棳嶌梡乿偲屇傃傑偡丅
壓恾偺傛偆偵俶宆丄俹宆丄俶宆偲僒儞僪僀僢僠忬偵敿摫懱傪愙崌偟偨慺巕偑丄乮僶僀億乕儔乯僩儔儞僕僗僞偱偡丅乮俹俶俹偲愙崌偟偨傕偺傕偁傝傑偡乯
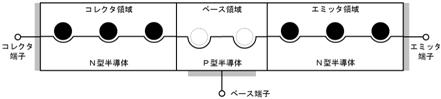
僟僀僆乕僪偲摨條偵丄俶宆椞堟偺揹巕偑丄俹宆椞堟偺儂乕儖偲寢崌偟丄壓恾偵奃怓偱帵偡傛偆偵丄儀乕僗偺嵍塃偵愨墢惈偺嬻朢憌偑惗偠傑偡丅
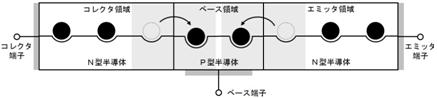
偝偰丄壓恾偺傛偆偵僐儗僋僞偵亄丄僄儈僢僞偵亅偺崅偄揹埑傪壛偊傞偲丄儀乕僗椞堟偺寠偑乮僄儈僢僞偐傜擖傝崬傫偩乯揹巕偱杽傔傜傟偰儀乕僗偑愨墢惈偲側傝丄傑偨丄僐儗僋僞懁偺揹巕偼嵍懁偺亄揹埑偵堷偐傟偰嬻朢憌偑峀偑傝丄揹棳偑棳傟傑偣傫丅
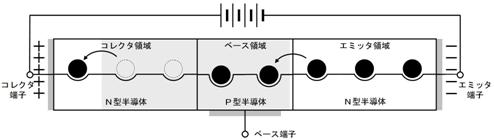
偙偙偱壓恾偺傛偆偵丄儀乕僗偵嬐偐側亄偺揹埑傪壛偊傑偡丅
偡傞偲丄偙偺亄偺揹埑偵堷偐傟偰丄儀乕僗偺寠傪杽傔偰偄偨揹巕偑敳偒庢傜傟丄儀乕僗椞堟偵寠乮僉儍儕傾丗儂乕儖乯偑偱偒傑偡丅偝傜偵丄偙偺寠偵堷偐傟偰乮寠偵擖傠偆偲偟偰乯丄僄儈僢僞偐傜儀乕僗傊丄師乆偲揹巕偑旘傃崬傫偱偒傑偡丅
偲偙傠偑丄儀乕僗偑敄偄偨傔旘傃崬傫偱偒偨揹巕偺戝晹暘偼寠偵擖傞偙偲偑偱偒偢丄僐儗僋僞椞堟偵擖偭偰偟傑偄傑偡丅偦偟偰丄堦扷僐儗僋僞偵擖偭偨偑嵟屻丄揹巕偼僐儗僋僞偵壛偊傜傟偨崅偄揹埑偵堷偐傟偰丄堦婥偵嵍傊恑傒丄僐儗僋僞抂巕偐傜奜傊弌偰峴偒傑偡丅
僄儈僢僞偐傜旘傃崬傫偱棃偨揹巕偺傎傫偺堦晹偩偗偑丄儀乕僗偺寠偵擖傝傑偡偐傜丄儀乕僗偐傜敳偒庢傞揹巕偼嬐偐偱偡傒傑偡丅
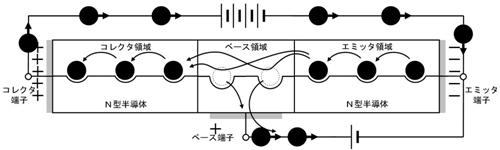
偙偺寢壥丄儀乕僗偐傜嬐偐側揹巕傪敳偒庢傞偩偗偱丄偦偺壗攞傕偺揹巕偑僄儈僢僞偐傜僐儗僋僞偵棳傟傑偡丅偁偨偐傕丄儀乕僗偵棳偟偨嬐偐側揹棳偑戝偒偔側偭偰丄僐儗僋僞偵棳傟偨傛偆偵尒偊傑偡偐傜丄偙偺傛偆側摥偒傪乽憹暆嶌梡乿偲屇傃傑偡丅
俆. 僟僀僆乕僪
俹俶愙崌偵偼壓恾偵帵偡傛偆側丄惍棳嶌梡乮侾曽岦偵偩偗揹棳傪棳偡嶌梡乯偑偁傝傑偟偨丅揹棳偼俹宆偐傜俶宆偵岦偐偭偰偩偗棳傟傑偡丅偙偺傛偆側揹棳傪乽弴揹棳乮弴曽岦揹棳乯乿俬俥丄偙偺偲偒壛偊偰偄傞揹埑傪乽弴揹埑乮弴曽岦揹埑乯乿倁俥偲屇傃傑偡丅乮棳傟側偄岦偒偵柍棟棳偟偨揹棳傪媡揹棳俬俼丄偦偺帪偺揹埑傪媡揹埑倁俼偲傕屇傃傑偡乯
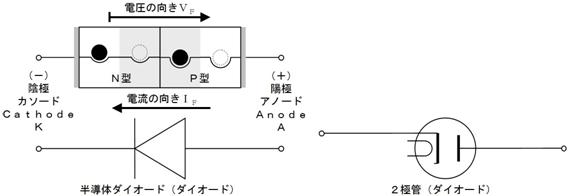
敿摫懱偑尰傟傞埲慜丄偙偺傛偆側梡搑偵偼忋恾塃懁偺丄俀嬌娗乮僟僀僆乕僪乯偑棙梡偝傟偰偄傑偟偨丅偙偺偨傔丄敿摫懱偱嶌偭偨惍棳慺巕乮忋恾嵍乯傕丄敿摫懱僟僀僆乕僪乮棯偟偰丄僟僀僆乕僪乯偲屇偽傟傑偡丅
俀嬌娗偵側傜偭偰俹宆偺抂巕傪傾僲乕僪乮俙乯丄俶宆偺抂巕傪僇僜乕僪乮俲乯偲屇傃傑偡丅僇僜乕僪偺捲傝偼庡偵乽俠倎倲倛倧倓倕乿偱偡偑丄棯岅偑乽俲乿側偺偼乽俲倎倲倛倧倓倕乿偲傕捲傝摼傞偐傜偱偡丅
偝偰丄壓恾嵍懁偺僌儔僼偵帵偡偲偍傝丄僟僀僆乕僪偵嬐偐偱傕弴揹棳乮俬俥乯傪棳偡偲丄僟僀僆乕僪偺椉抂偵偼侽丏俈倁掱搙偺弴揹埑乮倁俥乯偑惗偠丄揹棳傪憹傗偟偰傕丄弴揹埑偼彮偟偟偐忋徃偟傑偣傫丅
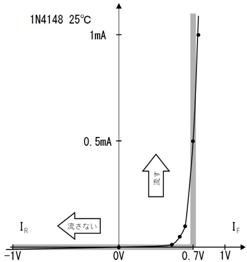
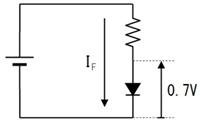
偦偙偱戝嶨攃側夞楬愝寁偱偼丄乽弴揹棳偑棳傟偰偄傞僔儕僐儞僟僀僆乕僪偵偼侽丏俈倁偺弴揹埑偑敪惗偟偰偄傞乿乮忋恾塃懁乯偲峫偊傑偡丅偮傑傝丄杮摉偼妸傜偐側嬋慄傪昤偄偰偄傞僟僀僆乕僪偺摿惈傪丄忋恾偵奃怓偺懢慄偱帵偡媡俴宆偵娙棯壔偟偰乮妝偵乯埖偄傑偡丅
僔儕僐儞僟僀僆乕僪偺弴揹埑偼壏搙偑侾亷忋徃偡傞偲丄俀倣倁尭彮偟傑偡丅偮傑傝丄忢壏偱栺侽丏俈倁偺弴揹埑偼丄俆侽亷忋徃偡傟偽栺侽丏俇倁偵丄侾侽侽亷忋徃偡傟偽栺侽丏俆倁偵掅壓偟傑偡丅偙偺偨傔丄峀偄壏搙斖埻偱摦嶌偝偣傞夞楬丄揹棳偑懡偔棳傟偰慺巕偺壏搙偑忋徃偡傞夞楬丄惓妋偵摦嶌偝偣傞夞楬丄摍偱偼弴揹埑偺曄壔偑塭嬁偟側偄傛偆偵岺晇傪峴偄傑偡丅
俇.侾. 楙廗
壓恾偺夞楬偱僟僀僆乕僪偵棳傟傞弴揹棳傪丄壓昞偵彂偒崬傒側偑傜媮傔偰偔偩偝偄丅
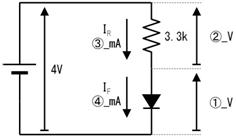
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僟僀僆乕僪偺弴抂揹埑偼丄
|
倁
|
|
嘇
|
揹抮偑係倁偩偐傜丄掞峈偺椉抂揹埑偼丄
|
倁
|
|
嘊
|
掞峈偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘋
|
僟僀僆乕僪偵棳傟傞弴揹棳俬俥偼丄
|
倣俙
|
俇.俀. 摎
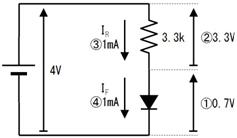
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僟僀僆乕僪偺弴揹埑偼丄
|
侽丏俈倁
|
|
嘇
|
揹抮偑係倁偩偐傜丄掞峈偺椉抂揹埑偼丄
|
俁丏俁倁
|
|
嘊
|
掞峈偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘋
|
僟僀僆乕僪偵棳傟傞弴揹棳俬俥偼丄
|
侾倣俙
|
僟僀僆乕僪偺弴揹埑偼壏搙偑侾亷忋偑傞偲丄栺俀倣倁壓偑傝傑偡丅侽丏俈倁偲峫偊偰偄傞弴揹埑偑丄壏搙偑俆侽亷壏搙偑忋偑傞偲丄侽丏俇倁偵尭彮偟傑偡偐傜乽懡彮弴揹埑偑曄壔偟偰傕戝忎晇乿側夞楬傪嶌傝傑偡丅
僔儕僐儞僟僀僆乕僪偵弴揹棳偑棳傟傞偲栺侽丏俈倁偺揹埑偑敪惗偟傑偟偨丅嵽椏偺堘偆僟僀僆乕僪偱偼丄偦傟偧傟師偺傛偆側弴揹埑偑敪惗偟傑偡丅
|
僟僀僆乕僪偺庬椶
|
弴揹埑乮倁俥乯
|
|
僎儖儅僯僂儉僟僀僆乕僪
|
栺侽丏俀倁
|
|
僔儑僢僩僉僶儕傾僟僀僆乕僪
|
栺侽丏俁倁
|
|
僔儕僐儞僟僀僆乕僪
|
栺侽丏俈倁
|
|
愒奜慄俴俤俢
|
栺侾丏俀倁
|
|
愒怓丒墿怓俴俤俢
掅婸搙椢怓俴俤俢
|
栺俀倁
|
|
惵怓丒敀怓俴俤俢
崅婸搙椢怓俴俤俢
|
栺俁丏俆倁
|
俈.侾. 楙廗
壓恾偺夞楬偱愒怓俴俤俢偵侾侽倣俙偺揹棳傪棳偟偰揰摍偟偨偄丅壓昞偵彂偒崬傒側偑傜丄掞峈抣傪寛傔偰偔偩偝偄丅
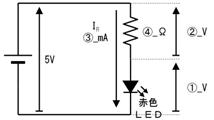
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
愒怓俴俤俢偵揹棳偑棳傟偨偲偒丄弴揹埑偼丄
|
倁
|
|
嘇
|
揹尮偑俆倁偩偐傜丄掞峈偺椉抂揹埑偼丄
|
倁
|
|
嘊
|
掞峈偵棳傟傞揹棳偼乮俴俤俢偲摍偟偄偐傜乯丄
|
倣俙
|
|
嘋
|
掞峈抣偼乮僆乕儉懃傛傝乯丄
|
兌
|
俈.俀. 摎
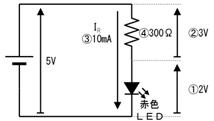
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
愒怓俴俤俢偵揹棳偑棳傟偨偲偒丄弴揹埑偼丄
|
俀倁
|
|
嘇
|
揹尮偑俆倁偩偐傜丄掞峈偺椉抂揹埑偼丄
|
俁倁
|
|
嘊
|
掞峈偵棳傟傞揹棳偼乮俴俤俢偲摍偟偄偐傜乯丄
|
侾侽倣俙
|
|
嘋
|
掞峈抣偼乮僆乕儉懃傛傝乯丄
|
俁侽侽兌
|
俉. 僟僀僆乕僪偺媡揹埑
僟僀僆乕僪偵弴揹棳傪棳偡偲丄壓恾僌儔僼塃抂偵帵偡傛偆偵丄椺偊偽侽丏俈倁掱搙偺弴揹埑傪惗偠傑偟偨丅乮壓恾偺僌儔僼偱偼乮暆峀偄揹埑傪昞偡偨傔偵乯揹埑偺栚惙偑嵍塃偵埑弅偝傟偰偄傑偡乯
偲偙傠偱僟僀僆乕僪偵媡揹埑傪壛偊偰傕媡揹棳偼杦偳棳傟傑偣傫丅壓恾偺僌儔僼傪徻偟偔尒傞偲丄媡揹埑傪壛偊偰傕丄嬌嬐偐側揹棳偑楻傟傞偩偗偱偡丅偙偺揹棳偑媡揹棳俬俼偱偡丅
偦偟偰丄媡揹埑傪偳傫偳傫崅傔偰峴偔偲丄壓恾偵乽堦斒僟僀僆乕僪乿偺僌儔僼偱帵偡傛偆偵丄偲偆偲偆僟僀僆乕僪偺懴揹埑傪挻偊偰揹棳偑棳傟巒傔傑偡丅偙偺尰徾傪僽儗乕僋僟僂儞乮崀暁乯偲屇傃傑偡丅僽儗乕僋僟僂儞傪婲偙偡偲寖偟偔敪擬偡傞偨傔丄壓恾嵍壓偵亊報偱帵偡傛偆偵攋懝偟傑偡丅偙偺傛偆側攋懝偵帄傞壜擻惈偑偁傞媡揹埑偑乽媡揹埑偺愨懳嵟戝掕奿乿偱偡丅
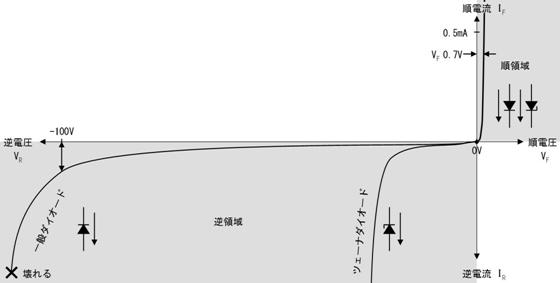
傑偨丄掅偄乮惓妋側乯揹埑偱埨慡偵僽儗乕僋僟僂儞偡傞傛偆偵惢憿偟偨僟僀僆乕僪偑丄忋恾偵帵偡乽僣僃乕僫僟僀僆乕僪乿偱偡丅僣僃乕僫僟僀僆乕僪偼掅偄揹埑偱僽儗乕僋僟僂儞偡傞埲奜偼堦斒僟僀僆乕僪偲杦偳摨偠惈幙傪帩偭偰偄傑偡丅
忋恾偐傜暘傞傛偆偵僣僃乕僫僟僀僆乕僪偐傜強掕偺揹埑傪庢傝弌偡応崌偼丄媡揹埑傪壛偊傑偡丅弴揹埑傪壛偊傞偲堦斒僟僀僆乕僪偲摨偠侽丏俈倁偺揹埑偑摼傜傟傞偩偗偱偡丅
俉.侾. 楙廗
僣僃乕僫揹埑俆倁偺僣僃乕僫僟僀僆乕僪傪巊偭偰壓恾偺夞楬傪嶌傝傑偟偨丅偦傟傟偧傟偺夞楬偺弌椡揹埑傪丄壓恾傪嶲峫偵壓昞偵彂偒崬傒側偑傜媮傔偰偔偩偝偄丅
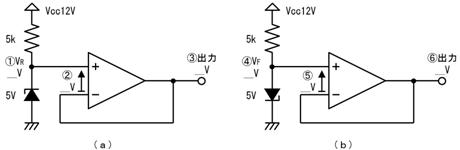
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僣僃乕僫僟僀僆乕僪偺椉抂揹埑偼丄
乮僣僃乕僫僟僀僆乕僪偵偼媡揹埑偑壛傢偭偰偄傞偐傜丄乯
|
倁
|
|
嘇
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
乮晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
倁
|
|
嘊
|
弌椡揹埑偼丄
|
倁
|
|
嘋
|
僣僃乕僫僟僀僆乕僪偺椉抂揹埑偼丄
乮僣僃乕僫僟僀僆乕僪偵偼弴揹埑偑壛傢偭偰偄傞偐傜丄乯
|
倁
|
|
嘍
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
乮晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
倁
|
|
嘐
|
弌椡揹埑偼丄
|
倁
|
俉.俀. 摎
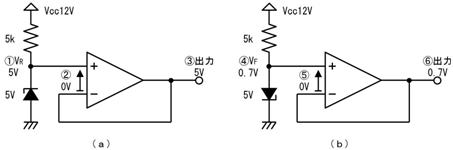
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僣僃乕僫僟僀僆乕僪偺椉抂揹埑偼丄
乮僣僃乕僫僟僀僆乕僪偵偼媡揹埑偑壛傢偭偰偄傞偐傜丄乯
|
俆倁
|
|
嘇
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
乮晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
侽倁
|
|
嘊
|
弌椡揹埑偼丄
|
俆倁
|
|
嘋
|
僣僃乕僫僟僀僆乕僪偺椉抂揹埑偼丄
乮僣僃乕僫僟僀僆乕僪偵偼弴揹埑偑壛傢偭偰偄傞偐傜丄乯
|
侽丏俈倁
|
|
嘍
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
乮晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
侽倁
|
|
嘐
|
弌椡揹埑偼丄
|
侽丏俈倁
|
俉.俁. 楙廗
僣僃乕僫揹埑俆倁丄掕奿懝幐俆侽侽倣倂偺僣僃乕僫僟僀僆乕僪傪俆倣倂偱摦嶌偝偣丄俆倁偺婎弨揹埑傪嶌傝傑偡丅壓昞偵婰擖偟側偑傜掞峈偺抣傪寛掕偟偰偔偩偝偄丅
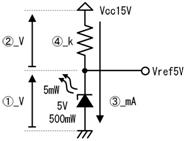
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僣僃乕僫僟僀僆乕僪偺僽儗乕僋僟僂儞揹埑偼丄
|
倁
|
|
嘇
|
掞峈偺椉抂揹埑偼丄
|
倁
|
|
嘊
|
僣僃乕僫僟僀僆乕僪偺敪擬傪俆倣倂偲偡傞偨傔偵偼丄僣僃乕僫僟僀僆乕僪偺媡揹棳偼丄
|
倣俙
|
|
嘋
|
掞峈偺抣偼丄
|
倠兌
|
俉.係. 摎
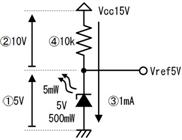
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僣僃乕僫僟僀僆乕僪偺僽儗乕僋僟僂儞揹埑偼丄
|
俆倁
|
|
嘇
|
掞峈偺椉抂揹埑偼丄
|
侾侽倁
|
|
嘊
|
僣僃乕僫僟僀僆乕僪偺敪擬傪俆倣倂偲偡傞偨傔偵偼丄僣僃乕僫僟僀僆乕僪偺媡揹棳偼丄
|
侾倣俙
|
|
嘋
|
掞峈偺抣偼丄
|
侾侽倠兌
|
俋. 僩儔儞僕僗僞
僩儔儞僕僗僞偵偼偄偔偮偐偺庬椶偑偁傝傑偡丅偙偙偱偼丄棟夝偟堈偄乽僶僀億乕儔丒僩儔儞僕僗僞乿傪乽僩儔儞僕僗僞乿偲屇傫偱庢傝忋偘傑偡丅僶僀億乕儔偱峫偊曽傪捦傔偽丄懠偺僩儔儞僕僗僞傕乮傂偲岺晇偡傞偙偲偱乯梕堈偵棟夝偱偒傑偡丅
偝偰丄偡偱偵乽俶俹俶愙崌偺憹暆嶌梡乿偱愢柧偟偨壓恾偺慺巕偑僩儔儞僕僗僞偱偡丅壓恾乮倎乯偼柾幃恾偱丄壓恾乮倐乯偼恾婰崋偱丄僩儔儞僕僗僞傪帵偟傑偡丅
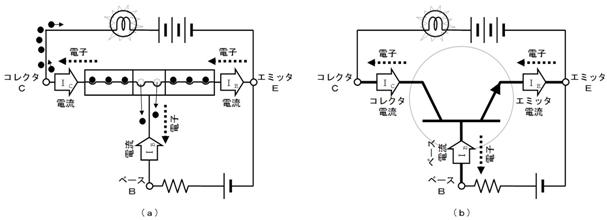
忋恾乮倎乯偺懢偄揰慄栴報偱帵偡偲偍傝丄乮俶俹俶宆偺乯僩儔儞僕僗僞偱偼丄儀乕僗偐傜揹巕傪堷偒敳偔偲丄僐儗僋僞偵戲嶳偺揹巕偑棳傟弌偰峴偒傑偟偨丅
晛捠偼乽揹巕偑棳傟傞乿偲偼尵傢偢乽揹棳偑棳傟傞乿偲愢柧偟傑偡丅揹棳偼揹巕偲斀懳偺曽岦偵棳傟傑偡偐傜丄僩儔儞僕僗僞偺摥偒偼丄忋恾偵僽儘僢僋栴報偱帵偡偲偍傝乽儀乕僗偵揹棳傪棳偟崬傓偲丄僐儗僋僞偵戝検偵揹棳偑棳傟崬傓乿偲愢柧偱偒傑偡丅
僩儔儞僕僗僞偵偼婛偵愢柧偟偨俶俹俶宆乮壓恾嵍懁乯偺懠偵俹俶俹宆乮壓恾塃懁乯偑偁傝傑偡丅
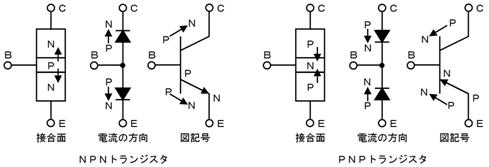
愙崌柺偱偼俹宆偐傜俶宆偵岦偐偭偰揹棳偑棳傟傑偡丅偱偡偐傜丄忋恾偱暘傞傛偆偵丄僟僀僆乕僪偱傕僩儔儞僕僗僞偱傕丄恾婰崋偺嶰妏傗栴報偼俹仺俶偺岦偒偵昤偐傟傑偡丅
忋恾嵍懁偱暘傞傛偆偵丄俶俹俶僩儔儞僕僗僞偱偼丄儀乕僗仺僄儈僢僞丄儀乕僗仺僐儗僋僞偺俀曽岦偵揹棳偑棳傟傑偡丅媡偵俹俶俹僩儔儞僕僗僞偱偼丄儀乕僗仼僄儈僢僞丄儀乕僗仼僐儗僋僞偺俀曽岦偵揹棳偑棳傟傑偡丅偙偺惈幙傪巊偊偽丄摫捠傪専嵏偡傞偙偲偱丄俶俹俶偐俹俶俹偐傪丄傑偨丄偳偺抂巕偑儀乕僗偱偁傞偐丄傪尒偮偗傞偙偲偑偱偒傑偡丅
侾侽.侾. 楙廗
僠僢僾僩儔儞僕僗僞傪僥僗僞偱摫捠専嵏偟偨偲偙傠丄壓恾偺俀偮偺愙懕偱揹棳偑棳傟傑偟偨丅敀偄僾儘乕僽偑亄懁偲偡傟偽丄儀乕僗抂巕偼嘆嘇嘊偺偳傟偱偡偐丅傑偨丄偙偺僩儔儞僕僗僞偺僞僀僾偼俶俹俶偱偡偐丄俹俶俹偱偡偐丅
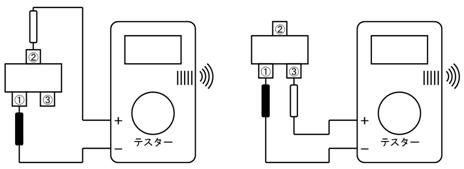
侾侽.俀. 摎
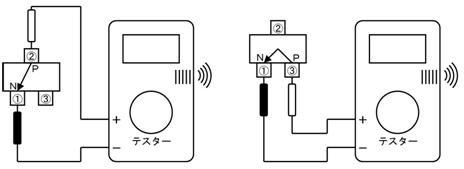
抂巕嘆偼丄嘇偐傜傕丄嘊偐傜傕揹棳偑棳傟崬傫偱偄傞偐傜儀乕僗偱偁傞丅儀乕僗偵揹棳偑棳傟崬傓偨傔偵偼乮愙崌柺偵揹棳偺棳傟傞曽岦偼丄俹仺俶偱偁傞偲峫偊傞偲乯僐儗僋僞偲僄儈僢僞偑俹宆丄儀乕僗偑俶宆敿摫懱偱偁傞偐傜丄偙偺僩儔儞僕僗僞偼俹俶俹宆偱偁傞丅
僩儔儞僕僗僞偵偼俀偮偺愙崌柺偑偁傝丄俶俹俶僩儔儞僕僗僞偺応崌偼丄俛仺俠偲俛仺俤偺岦偒偵揹棳偑棳傟傑偟偨丅傕偪傠傫偦偺媡偵偼揹棳偑杦偳棳傟傑偣傫丅偟偐偟拲堄偡傞偙偲偑偁傝傑偡丅
壓恾乮倎乯偵帵偡偲偍傝丄僐儗僋僞偲儀乕僗偺娫乮俠亅俛娫乯偵媡揹埑傪妡偗偰傕嬐偐側揹棳偑楻傟傞偩偗偱丄栤戣偁傝傑偣傫丅
偲偙傠偑丄壓恾乮倐乯偵帵偡傛偆偵丄僄儈僢僞偲儀乕僗偺娫乮俛亅俤娫乯偵媡揹埑傪妡偗傞偲丄揹埑偑掅偄応崌偼旝偐側揹棳偟偐楻傟偢栤戣偁傝傑偣傫偑丄揹埑偑俆倁掱搙偵側傞偲乮僽儗乕僋僟僂儞偑敪惗偟乯揹棳偑棳傟偰僩儔儞僕僗僞偑夡傟偰偟傑偟傑偡丅
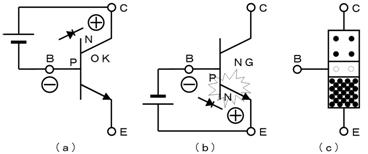
偙偺傛偆偵丄俛亅俤娫偺俹俶愙崌偼嬌傔偰媡揹埑偵庛偄偺偱丄夞楬傪峫偊傞偲偒傕拲堄偑昁梫偱偡丅
幚偼偙偺庛揰偼丄僩儔儞僕僗僞偺惈擻乮憹暆嶌梡乯傪崅傔傞偨傔偵惗偠偰偄傑偡丅偲偄偆偺傕丄僩儔儞僕僗僞偺憹暆嶌梡傪崅傔傞偵偼丄儀乕僗偵寠乮僉儍儕傾乯偑弌棃偨偲偒丄偱偒傞偩偗懡偔偺揹巕偑僄儈僢僞偐傜旘傃崬傫偱棃側偗傟偽偄偗傑偣傫丅偦偺偨傔偵丄忋恾乮們乯偺傛偆偵丄僄儈僢僞偵偼乮晛捠偺僟僀僆乕僪偵斾傋偰乯嬌傔偰戲嶳偺揹巕傪娷傑偣偰偁傝傑偡丅偁傑傝偵傕懡偔偺揹巕偑娷傑傟偰偄傞偨傔丄俛亅俤娫偺嬻朢憌偼愨墢惈偑埆偔側傝丄媡揹埑偑戝偒偔側傞偲揹棳偑棳傟偰偟傑偆偺偱偡丅
媡偵丄忋恾塃懁偵帵偡傛偆偵丄僐儗僋僞偵娷傑傟偰偄傞揹巕偼彮側偄偺偱丄俠亅俛娫偼僟僀僆乕僪偲摨條偵丄媡揹埑傪壛偊偰傕暯婥偱丄媡揹埑傪壛偊偰巊梡偟傑偡丅偲偼偄偊丄偙傟傕僟僀僆乕僪偲摨條偵丄壓恾乮倎乯偵帵偡傛偆偵丄嬐偐側媡揹棳偑楻傟傑偡丅偙偺媡揹棳偼僩儔儞僕僗僞偺摦嶌偵埆塭嬁傪梌偊傞応崌偑偁傞偺偱丄俬俠俛俷偲屇傫偱僨乕僞僔乕僩偵抣偑婰嵹偝傟偰偄傑偡丅
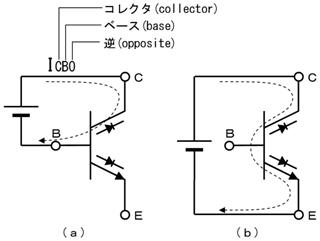
傑偨丄忋恾乮倐乯偺傛偆偵丄乮儀乕僗偵壗傕愙懕偣偢乯俠亅俤娫偵揹埑傪壛偊偨応崌傕俬俠俛俷偑棳傟傑偡丅僐儗僋僞偐傜儀乕僗偵棳傟偨俬俠俛俷偼丄儀乕僗偐傜僄儈僢僞偵棳傟偰峴偒傑偡丅
壓恾偼俶俹俶僩儔儞僕僗僞偺儀乕僗偵嬐偐側乮侾偺乯揹棳傪棳偟偨偲偙傠丄僐儗僋僞偵戲嶳偺乮侾侽侽偺乯揹棳偑棳傟偨條巕偱偡丅
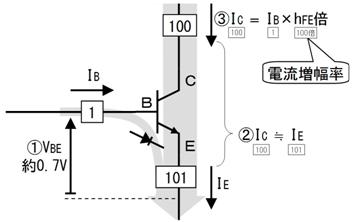
忋恾偺拞偵戝嶨攃側愝寁偱棙梡偡傞丄壓昞偵帵偡乽僩儔儞僕僗僞偺廳梫側惈幙乿偑慡偰娷傑傟偰偄傑偡丅
僩儔儞僕僗僞偺廳梫側惈幙
|
斣崋
|
億僀儞僩
|
愢柧
|
|
嘆
|
倁俛俤 佮 侽丏俈倁
|
儀乕僗偲僄儈僢僞偺娫偼乮懴埑偼掅偄偲偼尵偊乯俹俶愙崌偱偡偐傜丄僟僀僆乕僪偲摨條偵丄揹棳偑棳傟傞偲乮揹棳偵傛傝懡彮偺曄壔偼偁傞傕偺偺乯栺侽丏俈倁偺揹埑偑敪惗偟傑偡丅
|
|
嘇
|
俬俠 佮 俬俤
|
忋恾偱偼俬俠偑
侾侽侽 棳傟偨偲偒丄俬俤偑 侾侽侾
棳傟傑偡丅堘偄偼侾亾偱偡丅戝嶨攃側夞楬愝寁偱偼椉幰偑摨偠偲峫偊偰栤戣偁傝傑偣傫丅
|
|
嘊
|
俬俠 亖 俬俛
亊 倛俥俤
|
儀乕僗俬俛揹棳偑憹暆偝傟偰僐儗僋僞揹棳俬俠偵側傝傑偡丅忋恾偱偼侾侽侽攞偵憹暆偝傟偰偄傑偡偑昳庬偵傛偭偰堎側傞偺偱丄偙偺攞棪乮憹暆棪乯傪倛俥俤偲屇傃傑偡丅
|
侾俁.侾. 楙廗
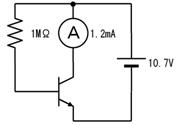
忋恾偺夞楬偱揹棳寁偑侾丏俀倣俙傪帵偟傑偟偨丅僩儔儞僕僗僞偺倛俥俤偼壗攞偱偡偐丅壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜峫偊偰偔偩偝偄丅
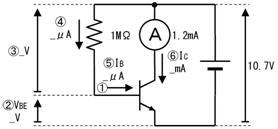
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
侾俵兌偑偁傞偨傔丄儀乕僗揹棳偼丄
乮慖傫偱偔偩偝偄乯
|
棳傟偰偄傞
棳傟偰偄側偄
|
|
嘇
|
儀乕僗揹棳偑棳傟偰偄傞偲偒丄儀乕僗僄儈僢僞娫揹埑
倁俛俤偼丄
|
栺丂丂丂丂倁
|
|
嘊
|
揹尮揹埑偑侾侽丏俈倁偩偐傜丄侾俵兌偺椉抂揹埑偼丄
|
倁
|
|
嘋
|
侾俵兌偵棳傟傞揹棳偼丄
|
兪俙
|
|
嘍
|
儀乕僗揹棳偼丄
|
兪俙
|
|
嘐
|
僐儗僋僞揹棳偼丄
|
倣俙
|
|
嘑
|
倛俥俤偼丄
|
攞
|
侾俁.俀. 摎
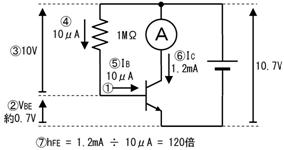
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
侾俵兌偑偁傞偨傔丄儀乕僗揹棳偼丄
|
棳傟偰偄傞
棳傟偰偄側偄
|
|
嘇
|
儀乕僗揹棳偑棳傟偰偄傞偲偒丄倁俛俤偼丄
|
栺侽丏俈倁
|
|
嘊
|
揹尮揹埑偑侾侽丏俈倁偩偐傜丄侾俵兌偺椉抂揹埑偼丄
|
侾侽倁
|
|
嘋
|
侾俵兌偵棳傟傞揹棳偼丄
|
侾侽兪俙
|
|
嘍
|
儀乕僗揹棳偼丄
|
侾侽兪俙
|
|
嘐
|
僐儗僋僞揹棳偼丄
|
侾丏俀倣俙
|
|
嘑
|
倛俥俤偼丄
|
侾俀侽攞
|
偮傑傝丄忋恾偺娙扨側夞楬偱倛俥俤偺抣傪抦傞偙偲偑偱偒傑偡丅乮應掕偟偰偄傞娫偵僩儔儞僕僗僞偑敪擬偟偰丄抣偑曄摦偡傞応崌偑偁傝傑偡乯
偙偺傛偆偵僩儔儞僕僗僞傪摦嶌偝偣傞偨傔偵丄堦掕偺揹棳傪棳偡偙偲傪乽僩儔儞僕僗僞傪僶僀傾僗偡傞乿偲屇傃丄棳偟偰偄傞揹棳傪乽僶僀傾僗揹棳乿偲屇傃傑偡丅抂巕偺柤慜傪晅偗偰乽僐儗僋僞僶僀傾僗揹棳乿摍偲巊偆偙偲傕偁傝傑偡丅傕偪傠傫乽僐儗僋僞僶僀傾僗揹棳乿偼乽僐儗僋僞揹棳乿偲屇傫偱傕娫堘偄偱偼偁傝傑偣傫丅偟偐偟丄僙儞僒偑敪偟偨怣崋摍偱丄堦帪揑偵僩儔儞僕僗僞偵揹棳偑棳傟偨応崌摍偼丄乮堦掕偺揹棳偑偟偽傜偔懕偄偰傕乯僶僀傾僗揹棳偲偼屇傃傑偣傫丅
侾俁.俁. 楙廗
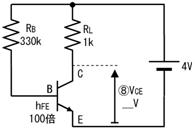
忋恾偺夞楬偺僐儗僋僞僄儈僢僞娫揹埑乮倁俠俤乯傪丄壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜媮傔偰壓偝偄丅
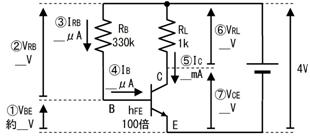
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺倁俛俤偼丄
|
丂丂丂倁
|
|
嘇
|
儀乕僗掞峈俼俛偺椉抂揹埑倁俼俛偼丄
|
倁
|
|
嘊
|
儀乕僗掞峈俼俛偵棳傟傞揹棳俬俼俛偼丄
|
兪俙
|
|
嘋
|
儀乕僗揹棳俬俛偼丄
|
兪俙
|
|
嘍
|
倛俥俤偑侾侽侽偩偐傜丄僐儗僋僞揹棳俬俠偼丄
|
倣俙
|
|
嘐
|
晧壸掞峈俼俴偺椉抂揹埑倁俼俴偼丄
|
倁
|
|
嘑
|
僐儗僋僞僄儈僢僞娫揹埑倁俠俤偼丄
|
倁
|
侾俁.係. 摎
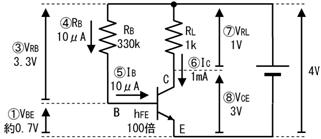
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺倁俛俤偼丄
|
丂丂丂栺侽丏俈倁
|
|
嘇
|
儀乕僗掞峈俼俛偺椉抂揹埑倁俼俛偼丄
|
俁丏俁倁
|
|
嘊
|
儀乕僗掞峈俼俛偵棳傟傞揹棳俬俼俛偼丄
|
侾侽兪俙
|
|
嘋
|
儀乕僗揹棳俬俛偼丄
|
侾侽兪俙
|
|
嘍
|
倛俥俤偑侾侽侽偩偐傜丄僐儗僋僞揹棳俬俠偼丄
|
侾倣俙
|
|
嘐
|
晧壸掞峈俼俴偺椉抂揹埑倁俼俴偼丄
|
侾倁
|
|
嘑
|
僐儗僋僞僄儈僢僞娫揹埑倁俠俤偼丄
|
俁倁
|
仸僐儗僋僞偵愙懕偝傟偨晧壸掞峈俼俴偼丄僐儗僋僞掞峈俼俠偲屇偽傟傞応崌傕偁傝傑偡丅
偙偺傛偆偵丄揹尮偐傜掞峈堦杮偱儀乕僗偵揹棳傪棳偡曽朄傪乽屌掕僶僀傾僗乿偲屇傃傑偡丅夞楬偑娙扨偱丄儀乕僗揹棳偼堦掕偱偡偑丄寚揰偑偁傝傑偡丅
寚揰偺侾偮栚偼丄夞楬偺屄懱嵎偱偡丅摨堦昳庬偺僩儔儞僕僗僞偱傕丄慺巕枅偵倛俥俤偑戝偒偔偽傜偮偒傑偡丅乮偨偲偊偽丄俈侽乣俁侽侽攞偺斖埻偱乽塣擟偣乿偲偄偆応崌傕偁傝傑偡乯偙偺偨傔丄僐儗僋僞揹棳傪堦掕偵偡傞偵偼丄儀乕僗掞峈俼俛偺抣傪侾戜侾戜偺挷惍偡傞昁梫偑偁傝傑偡丅
寚揰偺俀偮栚偼丄倛俥俤偼壏搙偱傕曄壔偡傞偺偱丄揹尮傪擖傟偰慺巕偑壏傑傞偲僐儗僋僞揹棳偑曄壔偟傑偡丅摿偵戝偒側揹棳傪棳偡応崌偼敪擬偑戝偒偔揹棳偺曄壔偑栚棫偪傑偡丅
廬偭偰丄壓恾偺傛偆偵儀乕僗揹棳傪挷愡偱偒傞傛偆偵偡傟偽乮壏搙偵傛傞揹棳偺曄壔偼懡彮偁傞偗傟偳乯丄杮楙廗偺夞楬偱怣崋傪憹暆偡傞偙偲偑偱偒傑偡丅揹埑憹暆棪傕侾俆侽攞掱搙偲偐側傝戝偒偄偱偡丅乮憹暆棪偺媮傔曽偼屻偱愢柧偟傑偡乯
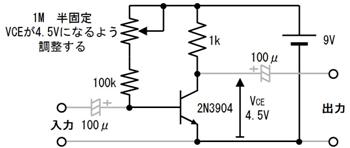
偲偼偄偊丄偙偺傛偆側挷愡偼尰幚揑偱偼偁傝傑偣傫偐傜丄屻偱愢柧偡傞傛偆側丄倛俥俤偑僶儔偮偄偰傕丄偦偺塭嬁傪庴偗偢偵摦嶌偡傞夞楬偑梡偄傜傟傑偡丅
僩儔儞僕僗僞偵偼掞峈偲堘偄丄僆乕儉懃偵偼廬傢偢丄揹埑偑曄壔偟偰傕堦掕偺揹棳傪棳偦偆偲偡傞惈幙乮掕揹棳摿惈乯偑偁傝傑偡丅偙偺掕揹棳摿惈偼條乆側敿摫懱慺巕偱尰傟傑偡丅
侾係.侾. 楙廗
愭偵墘廗偟偨壓恾乮倎乯偺夞楬偱偼丄僐儗僋僞揹棳俬俠偑侾倣俙棳傟偰偄傑偟偨丅偙偺夞楬偺晧壸掞峈俼俴傪僔儑乕僩偟丄壓恾乮倐乯偺夞楬偵曄峏偡傞偲丄僐儗僋僞揹棳俬俠偲僐儗僋僞僄儈僢僞娫揹埑倁俠俤偼偳偺傛偆偵曄壔偟傑偡偐丅壓昞偵婰擖偟側偑傜媮傔偰偔偩偝偄丅
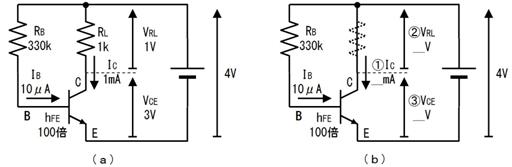
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
儀乕僗揹棳偲倛俥俤偐傜丄俬俠偼丄
|
倣俙
|
|
嘇
|
僔儑乕僩偟偨倁俼俴偺椉抂揹埑偼丄
|
倁
|
|
嘊
|
揹尮揹埑係倁偩偐傜丄倁俠俤偼丄
|
倁
|
侾係.俀. 摎
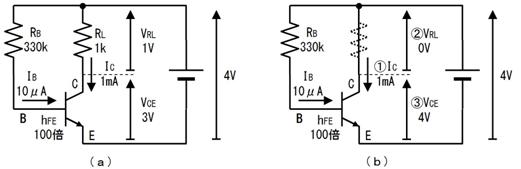
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
儀乕僗揹棳偲倛俥俤偐傜丄俬俠偼丄
|
侾倣俙
|
|
嘇
|
僔儑乕僩偟偨倁俼俴偺椉抂揹埑偼丄
|
侽倁
|
|
嘊
|
揹尮揹埑係倁偩偐傜丄倁俠俤偼丄
|
係倁
|
偙偺傛偆偵丄晧壸乮俼俴乯偑曄壔偟丄倁俠俤偑曄壔乮俁倁仺係倁乯偟偰傕丄棳傟傞揹棳乮俬俠乯偼曄壔偣偢堦掕偱偡丅偙偺傛偆側惈幙傪乽掕揹棳摿惈乿偲屇傃傑偡丅
壓恾偵帵偡僨乕僞僔乕僩偺倁俠俤亅俬俠摿惈恾偼偙偺條巕傪昞偟偨僌儔僼偱丄條乆側儀乕僗揹棳偱丄倁俠俤傪曄壔偝偣偨偲偒偺俬俠偲偺娭學傪僌儔僼偵昤偄偨傕偺偱偡丅
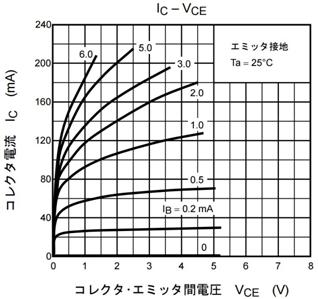
偨偲偊偽丄忋恾壓偐傜俀斣栚偺俬俛亖侽丏俀倣俙偺僌儔僼偱偼丄倁俠俤偑侽丏俆倁乣俆倁偺斖埻偱僌儔僼偑悈暯偱丄俬俠偼俁侽倣俙掱搙偱杦偳曄壔偑偁傝傑偣傫丅偙偺悈暯側乮揹埑偑曄傢偭偰傕揹埑偑曄傢傜側偄乯晹暘偑掕揹棳摿惈傪帵偟偰偄傑偡丅扐偟丄俬俛亖俁倣俙偺椺偱暘傞傛偆偵丄僐儗僋僞揹棳偑揹棳偑戝偒偔側傞偲掕揹棳摿惈偑晄姰慡偲側偭偰丄僌儔僼偑孹偒傑偡丅
倛俥俤偺抣偼摨偠昳庬偱傕戝偒偔堎側傝傑偡丅壓昞偺傛偆偵丄椺偊偽俀俶俁俋侽係傪俬俠傪侾倣俙偺偱巊梡偟偨偲偒偺倛俥俤偼俈侽乣俁侽侽攞偲丄嵟戝係攞埲忋偺奐偒偑偁傝傑偡丅
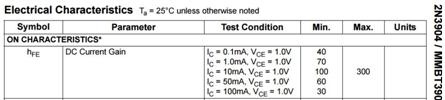
偙偺傛偆側倛俥俤偺戝偒側僶儔僣僉傪娚榓偡傞偨傔偵丄昳庬傗儊乕僇乕偵傛偭偰偼丄壓昞偺傛偆偵丄昳斣偵乽倛俥俤暘椶乿傪捛壛偟偰丄暘椶乮慖暿乯偟偰斕攧偟偰偄傞応崌傕偁傝傑偡丅
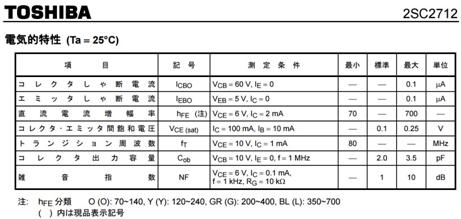
忋昞棑奜偵婰嵹偺乽倛俥俤暘椶乿偑偙傟傪昞偟丄偨偲偊偽俀俽俠俀俈侾俀亅倄側傜倛俥俤暘椶偼乽倄乿偱丄倛俥俤偺抣偼侾俀侽乣俀係侽攞偲丄俀攞掱搙偺奐偒偵廂傑傞傛偆偵暘椶偝傟偰偄傑偡丅
暘椶偺柤慜偼丄俷乮僆儗儞僕乯丄倄乮儂儚僀僩乯丄俧俼乮僌儕乕儞乯丄俛俴乮僽儖乕乯偲怓偵娭學偟偰偄傞応崌偑偁傝傑偡丅庤嶌嬈偱暘椶偟偰偄偨帪戙偵丄嵶昅傪巊偭偰怓儁儞僉偱彫偝側揰傪晅偗丄暘椶傪昞帵偟偰偄偨柤巆偱偡丅
壓恾偺傛偆偵丄儀乕僗偵堦掕偺揹埑傪壛偊傞夞楬偱偼丄乮倁俛俤偑壏搙偱掅壓偡傞偨傔乯壏搙偑忋徃偡傞偲儀乕僗揹棳傗僄儈僢僞揹棳偑憹壛偟傑偡丅
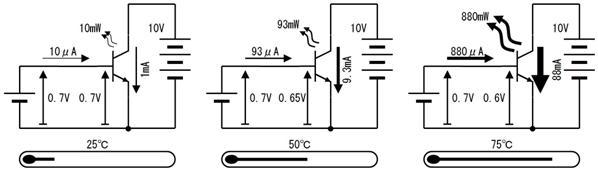
堦扷揹棳偑憹偊傞偲丄乽乮憹偊偨揹棳偱乯僩儔儞僕僗僞偑敪擬偟偰壏搙偑忋徃偟丄乮倁俛俤偑掅壓偟偰乯偝傜偵揹棳偑憹偊傞乿偲偄偆楢嵔偑敪惗偟丄偮偄偵偼僩儔儞僕僗僞偑攋懝偟傑偡丅偙傟傪擬朶憱偲屇傃傑偡丅擬朶憱偼壓恾偺傛偆偵丄僄儈僢僞偵掞峈傪憓擖偡傞偲杊巭偱偒傑偡丅
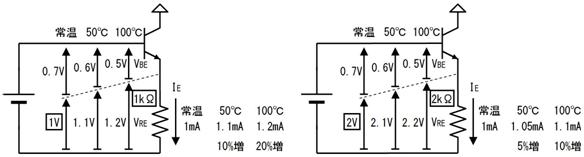
忋恾嵍偱偼僄儈僢僞偵侾倠兌傪憓擖偟乮掞峈偺椉抂揹埑傪侾倁偲偟偰乯俆侽搙偺壏搙忋徃偱丄揹棳偺憹壛傪侾侽亾憹偵梷偊偰偄傑偡丅摨恾塃偱偼丄俀倠兌傪憓擖偟乮掞峈偺椉抂揹埑傪俀倁偲偟偰乯揹棳偺憹壛傪俆亾偵梷偊偰偄傑偡丅
偙偺傛偆偵丄僄儈僢僞掞峈傪戝偒偔偟偰丄掞峈偺椉抂揹埑傪崅偔偡傞偲丄僄儈僢僞揹棳偺埨掕惈偑崅傑傝傑偡丅偟偐偟僄儈僢僞掞峈傪戝偒偔偡傞偲憹暆棪偑壓偑傝傑偡偐傜丄彫偝側揹埑傪埖偆夞楬偱偼丄僄儈僢僞掞峈偺椉抂揹埑傪侾倁掱搙偵慖傇偺偑堦斒揑偱偡丅
偙偺夞楬偱偼僄儈僢僞揹棳俬俤偑憹壛偡傞偲乮僄儈僢僞掞峈偺椉抂揹埑偑忋徃偟偰乯儀乕僗揹棳俬俛偑尭彮偟傑偡丅偮傑傝丄揹棳俬俤憹壛仺揹棳俬俛尭彮丄偲偄偆晧婣娨偱乮僶僀傾僗揹棳傪乯埨掕偝偣偰偄傞偺偱乽揹棳婣娨僶僀傾僗夞楬乿偲屇傃傑偡丅
乽揹棳婣娨僶僀傾僗夞楬乿偼擔杮撈帺偺屇傃柤偱丄塸岅偱偼乽僄儈僢僞丒僨僕僃僱儗乕僔儑儞乿乮僄儈僢僞偺梷惂乯偲暿偺柤慜偱屇偽傟傑偡丅擔杮岅傪捈栿偟偰乽僇儗儞僩丒僼傿乕僪僶僢僋丒僶僀傾僗丒僒乕僉僢僩乿偲尵偭偰傕丄傑傞偱捠偠傑偣傫丅
偝傜偵偙偺夞楬偱偼丄倛俥俤偑曄摦偟偰傕乮俬俛偼曄摦偟傑偡偑乯俬俤傗俬俠偼杦偳曄壔偟傑偣傫丅側偤側傜丄倛俥俤偑戝偒偔偰俬俤偑懡偔棳傟傞偲丄僄儈僢僞掞峈偺椉抂揹埑偑憹偊偰丄儀乕僗揹棳偑尭傞偐傜偱偡丅
偮傑傝丄僄儈僢僞掞峈傪憓擖偡傞帠偵傛偭偰丄倁俛俤偺壏搙曄壔傗倛俥俤偺僶儔僣僉偺憃曽傪梷惂偟偰丄埨掕偟偨僄儈僢僞揹棳傪棳偡偙偲偑偱偒傑偡丅
僩儔儞僕僗僞偼堦掕偺揹棳偑棳傟傞傛偆偵岺晇偟偰丄埨掕摦嶌偝偣傑偡丅婛偵愢柧偟偨儀乕僗偵堦掕偺揹棳傪棳偡曽朄偱偼丄倛俥俤偺偽傜偮偒偱僄儈僢僞揹棳傕偽傜偮偔寚揰偑偁傝傑偟偨丅
偦偙偱壓恾偺傛偆偵丄儀乕僗偵堦掕偺揹埑傪壛偊丄僄儈僢僞偵掞峈俼俤傪庢傝晅偗傞偲乮憹暆棪偼壓偑傝傑偡偑乯乮壏搙偱倁俛俤偑曄壔偟偰傕丄倛俥俤偺偽傜偮偄偰傕乯埨掕偟偨僄儈僢僞揹棳傪棳偡偙偲偑偱偒傑偟偨丅
偙偺夞楬偺傛偆偵丄儀乕僗偵壛偊傞堦掕偺揹埑傪丄儀乕僗僶僀傾僗揹埑偲屇傃傑偡丅偱偼丄偙偺夞楬偵偮偄偰専摙偟傑偡丅
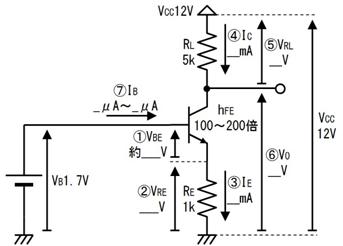
侾俈.侾. 楙廗
忋恾傪尒側偑傜壓昞偵婰擖偟偰丄奺晹偺揹棳丄揹埑傪媮傔偰壓偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺倁俛俤偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘆傛傝乯
|
倁
|
|
嘇
|
僄儈僢僞掞峈俼俤偺偺椉抂揹埑倁俼俤偼丄
|
丂倁
|
|
嘊
|
僄儈僢僞揹棳俬俤偼丄
|
俙
|
|
嘋
|
僐儗僋僞揹棳俬俠偼丄
乮乽僩儔儞僕僗僞偺廳梫側惈幙嘇乿偵傛傟偽乯
|
俙
|
|
嘍
|
晧壸掞峈俼俴偺椉抂揹埑倁俼俴偼丄
|
倁
|
|
嘐
|
揹尮揹埑偑侾俀倁偩偐傜丄弌椡揹埑倁俷偼丄
|
倁
|
|
嘑
|
儀乕僗揹棳俬俛偺斖埻偼丄
乮乽僩儔儞僕僗僞偺廳梫側惈幙嘊偵乿偵傛傟偽乯
|
兪俙乣
兪俙
|
侾俈.俀. 摎
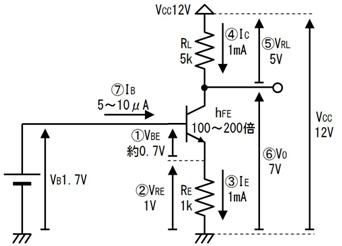
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺倁俛俤偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘆傛傝乯
|
栺侽丏俈倁
|
|
嘇
|
僄儈僢僞掞峈俼俤偺偺椉抂揹埑倁俼俤偼丄
|
侾倁
|
|
嘊
|
僄儈僢僞揹棳俬俤偼丄
|
侾倣俙
|
|
嘋
|
僐儗僋僞揹棳俬俠偼丄
乮乽僩儔儞僕僗僞偺廳梫側惈幙嘇乿偵傛傟偽乯
|
侾倣俙
|
|
嘍
|
晧壸掞峈俼俴偺椉抂揹埑倁俼俴偼丄
|
俆倁
|
|
嘐
|
揹尮揹埑偑侾俀倁偩偐傜丄弌椡揹埑倁俷偼丄
|
俈倁
|
|
嘑
|
儀乕僗揹棳俬俛偺斖埻偼丄
乮乽僩儔儞僕僗僞偺廳梫側惈幙嘊偵乿偵傛傟偽乯
|
俆兪俙乣
侾侽兪俙
|
偙偺傛偆偵丄僄儈僢僞掞峈俼俤傪捛壛偟丄儀乕僗偵乮堦掕偺揹棳傪棳偡偺偱偼側偔乯堦掕偺揹埑倁俛傪壛偊傞偙偲偱丄倁俛俤偺壏搙曄壔傗倛俥俤偺僶儔僣僉偺塭嬁傪偁傑傝庴偗偢偵丄埨掕偟偨僐儗僋僞揹棳傪棳偡偙偲偑偱偒傑偡丅
侾俈.俁. 楙廗
壓恾偼忋偱楙廗偟偨夞楬偺丄傋乕僗揹埑倁俛傪侽丏侾倁偩偗憹傗偟偰偄傑偡丅儀乕僗揹埑憹壛偺塭嬁偵傛傞弌椡揹埑倁俷偺曄壔傪丄壓昞偵彂崬傒側偑傜媮傔偰偔偩偝偄丅
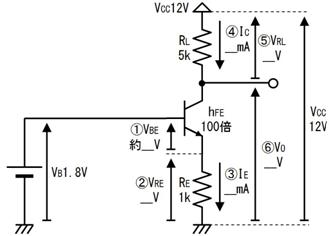
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺倁俛俤偼
乮僩儔儞僕僗僞偺廳梫側惈幙嘆傛傝乯
|
倁
|
|
嘇
|
僄儈僢僞掞峈俼俤偺偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘊
|
僄儈僢僞揹棳俬俤偼丄
|
倣俙
|
|
嘋
|
僐儗僋僞揹棳俬俠偼丄
乮乽僩儔儞僕僗僞偺廳梫側惈幙嘇乿偵傛傟偽乯
|
倣俙
|
|
嘍
|
晧壸掞峈俼俴偺椉抂揹埑倁俼俴偼丄
|
倁
|
|
嘐
|
揹尮揹埑偑侾俀倁偩偐傜丄弌椡揹埑倁俷偼丄
|
倁
|
|
嘑
|
儀乕僗揹埑倁俛偑侾丏俈倁偐傜丄侾丏俉倁偵丄
侽丏侾倁憹壛偟偨塭嬁偵傛傞丄弌椡揹埑倁俷偺曄壔偼丄
|
亅丂丂丂倁
|
|
嘒
|
擖椡揹埑偺曄壔偼壗攞偵側偭偰弌椡揹埑偵尰傟偰偄傞偐丅乮偙偺夞楬偺憹暆棪偼乯
|
亅丂丂丂攞
|
|
嘓
|
晧壸掞峈俼俴亐僄儈僢僞掞峈俼俤偺抣偼丄
|
|
侾俈.係. 摎
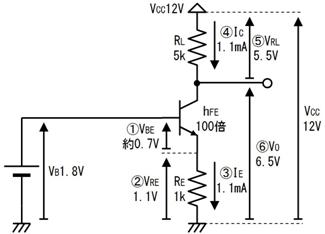
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺倁俛俤偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘆傛傝乯
|
栺侽丏俈倁
|
|
嘇
|
僄儈僢僞掞峈俼俤偺偺椉抂揹埑倁俼俤偼丄
|
侾丏侾倁
|
|
嘊
|
僄儈僢僞揹棳俬俤偼丄
|
侾丏侾倣俙
|
|
嘋
|
僐儗僋僞揹棳俬俠偼丄
乮乽僩儔儞僕僗僞偺廳梫側惈幙嘇乿偵傛傟偽乯
|
侾丏侾倣俙
|
|
嘍
|
晧壸掞峈俼俴偺椉抂揹埑倁俼俴偼丄
|
俆丏俆倁
|
|
嘐
|
揹尮揹埑偑侾俀倁偩偐傜丄弌椡揹埑倁俷偼丄
|
俇丏俆倁
|
|
嘑
|
儀乕僗揹埑倁俛偑侾丏俈倁偐傜丄侾丏俉倁偵丄
侽丏侾倁憹壛偟偨塭嬁偵傛傞丄弌椡揹埑倁俷偺曄壔偼丄
|
亅侽丏俆倁
|
|
嘒
|
擖椡揹埑偺曄壔偼壗攞偵側偭偰弌椡揹埑偵尰傟偰偄傞偐丅乮偙偺夞楬偺憹暆棪偼乯
|
亅俆攞
|
|
嘓
|
晧壸掞峈俼俴亐僄儈僢僞掞峈俼俤偺抣偼丄
俆倠亐侾倠亖俆
|
俆
|
偙偺傛偆偵丄僄儈僢僞掞峈偺偁傞夞楬偺憹暆棪乮偺栚埨乯偼丄晧壸掞峈俼俴亐僄儈僢僞掞峈俼俤偱媮傔傞偙偲偑偱偒傑偡乮僐儗僋僞掞峈俼俠亐僄儈僢僞掞峈俼俤偱媮傔傞偙偲偑偱偒傑偡乯丅
侾俈.俆. 楙廗
壓恾偺夞楬傪丄僐儗僋僞揹棳俬俠傪侾倣俙偱摦嶌偝偣偨偄偱偡丅乮乽僐儗僋僞揹棳偺摦嶌揰傪侾倣俙偵偟偨偄乿乽僐儗僋僞僶僀傾僗揹棳傪侾倣俙偵偟偨偄乿偲傕尵傢傟傑偡乯壓昞偵彂偒崬傒側偑傜丄僄儈僢僞掞峈俬俤偺抣傪寛掕偟偰偔偩偝偄丅
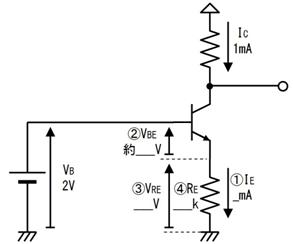
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僄儈僢僞揹棳偼丄
乮乽僩儔儞僕僗僞偺廳梫側惈幙嘇乿偵傛傟偽乯
|
倣俙
|
|
嘇
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘆傛傝乯
|
倁
|
|
嘊
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘋
|
僄儈僢僞掞峈偺抣俼俤偼丄
|
倠兌
|
侾俈.俇. 摎
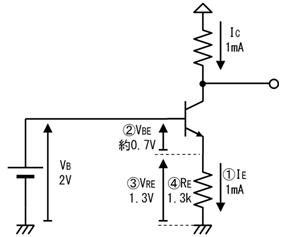
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僄儈僢僞揹棳偼丄
乮乽僩儔儞僕僗僞偺廳梫側惈幙嘇乿偵傛傟偽乯
|
侾倣俙
|
|
嘇
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘆傛傝乯
|
栺侽丏俈倁
|
|
嘊
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
|
侾丏俁倁
|
|
嘋
|
僄儈僢僞掞峈偺抣俼俤偼丄
|
侾丏俁倠兌
|
侾俈.俈. 楙廗
壓恾偺夞楬偱弌椡揹埑倁俷偑俆倁偲側傞傛偆偵丄壓昞偵彂偒崬傒側偑傜丄儀乕僗揹埑倁俛傪寛掕偟偰偔偩偝偄丅傑偨儀乕僗揹棳俬俛偺抣偺斖埻傪媮傔偰壓偝偄丅
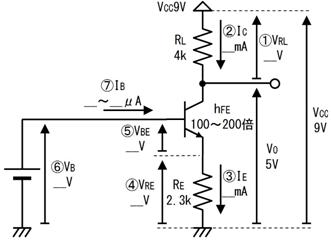
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
晧壸掞峈俼俴偺椉抂揹埑偼丄乮倁俠俠偲倁俷偐傜乯
|
倁
|
|
嘇
|
僐儗僋僞揹棳俬俠偼丄乮僆乕儉懃傛傝乯
|
倣俙
|
|
嘊
|
僄儈僢僞揹棳俬俤偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘇偵傛傟偽丄乯
|
倣俙
|
|
嘋
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄乮僆乕儉懃傛傝乯
|
倁
|
|
嘍
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘆傛傝乯
|
倁
|
|
嘐
|
儀乕僗揹埑倁俛偼丄乮僉儖僸揹埑懃傛傝乯
|
倁
|
|
嘑
|
儀乕僗揹棳俬俛偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘊傛傝乯
|
兪俙乣丂丂兪俙
|
侾俈.俉. 摎
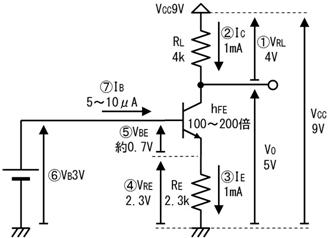
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
晧壸掞峈俼俴偺椉抂揹埑偼丄乮倁俠俠偲倁俷偐傜乯
|
係倁
|
|
嘇
|
僐儗僋僞揹棳俬俠偼丄乮僆乕儉懃傛傝乯
|
侾倣俙
|
|
嘊
|
僄儈僢僞揹棳俬俤偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘇偵傛傟偽丄乯
|
侾倣俙
|
|
嘋
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄乮僆乕儉懃傛傝乯
|
俀丏俁倁
|
|
嘍
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
乮僩儔儞僕僗僞偺廳梫側惈幙嘆傛傝乯
|
栺侽丏俈倁
|
|
嘐
|
儀乕僗揹埑倁俛偼丄乮僉儖僸揹埑懃傛傝乯
|
俁倁
|
|
嘑
|
儀乕僗揹棳俬俛偼丄乮僩儔儞僕僗僞偺廳梫側惈幙嘊傛傝乯
侾倣俙乛俀侽侽亖俆兪俙丂侾倣俙乛侾侽侽亖侾侽兪俙
|
俆兪俙乣侾侽兪俙
|
壓恾乮倎乯偺傛偆偵丄儀乕僗偵揹埑傪壛偊偰揹棳婣娨僶僀傾僗夞楬傪棙梡偡傞偙偲偱丄倁俛俤傗倛俥俤偑曄壔偟偰傕丄僐儗僋僞揹棳傪堦掕偵曐偮偙偲偑偱偒傑偟偨丅偟偐偟偙偺夞楬偼僶僀傾僗揹埑偵揹抮傪巊梡偟偰偍傝丄乮妱崅偱丄徚栒偡傞偨傔乯幚梡揑偱偼偁傝傑偣傫丅
偦偙偱壓恾乮倐乯偺傛偆偵丄掞峈傪巊偭偨暘埑夞楬偱侾丏俈倁傪敪惗偝偣傟偽丄揹抮傪巊傢偢偵嵪傒傑偡丅壓恾偺夞楬偼丄儀乕僗揹棳偑侾侽兪俙棳傟傞偙偲傕峫椂偟偰丄儀乕僗偵侾丏俈倁偺僶僀傾僗揹埑偑壛傢傞傛偆偵岺晇偟丄傑偨丄俼俙傗俼俛偺抣偼弌棃傞偩偗戝偒偔偟丄夞楬偺徚旓揹棳傕愡栺偟偨偮傕傝偱偡丅
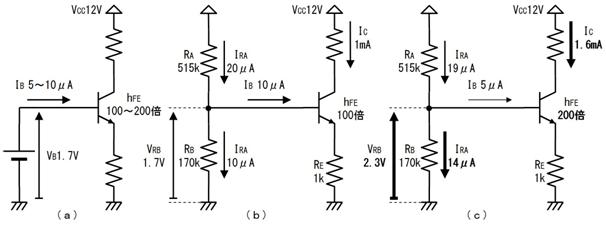
偲偙傠偑倛俥俤偵偼俀攞埲忋偺偽傜偮偒偑偁傞偨傔丄椺偊偽倛俥俤偑忋恾乮倐乯偺侾侽侽攞偐傜丄忋恾乮們乯偺俀侽侽攞偵曄傢偭偨応崌偼丄儀乕僗揹棳偑侾侽兪俙偐傜丄俆兪俙偵尭彮偟丄偦偺寢壥丄儀乕僗偵壛傢傞僶僀傾僗揹埑偑侾丏俈倁偐傜丄俀丏俁倁偲戝偒偔側偭偰偟傑偄傑偡丅
偙偺傛偆偵丄壓恾乮倎乯偺傛偆偵俼俙丄俼俛偵棳偡揹棳傪夁搙偵愡栺偡傞偲丄儀乕僗揹棳偺乮倛俥俤偵傛傞乯曄壔偱乮俼俙丄俼俛偺揹棳偑曄壔偟偰乯儀乕僗偺揹埑偑曄壔偟偰偟傑偄傑偡丅偦偙偱壓恾乮倐乯偵帵偡傛偆偵丄俼俙丄俼俛偵偼儀乕僗揹棳偺侾侽攞乣侾侽侽攞掱搙偺廫暘側揹棳傪棳偟丄儀乕僗揹棳偑曄壔偟偰傕俼俙丄俼俛偺揹棳偑塭嬁傪庴偗側偄傛偆偵偟傑偡丅乮戝偒側愳側傜丄彮偟偖傜偄悈傪媯傫偱傕丄愳偺棳傟偵塭嬁偟側偄偺偲摨偠偱偡乯
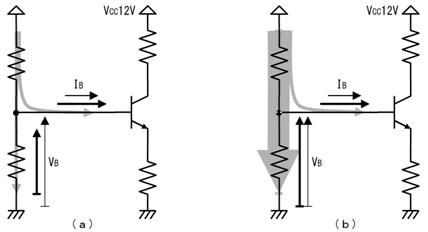
侾俉.侾. 楙廗
壓恾偺夞楬偱丄暘埑夞楬偺揹棳俬俼俛傪丄儀乕僗揹棳偺嵟戝抣偺俀侽攞偵愝掕偟偰丄儀乕僗僶僀傾僗揹埑傪侾丏俈倁梌偊傑偡丅壓昞偵婰擖偟側偑傜丄俼俙偲俼俛偺抣傪寛掕偟偰壓偝偄丅
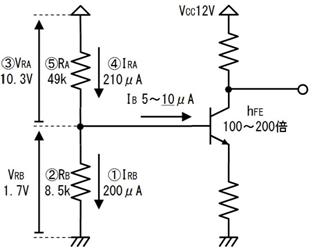
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俬俛偺嵟戝抣偺俀侽攞偵愝掕偡傞偐傜丄俬俼俛偼丄
|
兪俙
|
|
嘇
|
倁俛乮倁俼俛乯傪侾丏俈倁偵偡傞偨傔偵丄俼俛偼丄
|
倠兌
|
|
嘊
|
揹尮揹埑偑侾俀倁偩偐傜丄倁俼俙偼丄
|
倁
|
|
嘋
|
俬俼俙偼丄
|
兪俙
|
|
嘍
|
俼俙偼丄
|
倠兌
|
侾俉.俀. 摎
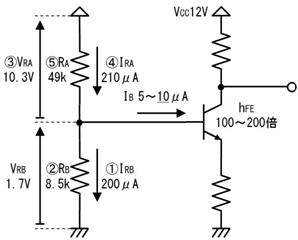
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俬俛偺嵟戝抣偺俀侽攞偵愝掕偡傞偐傜丄俬俼俛偼丄
|
俀侽侽兪俙
|
|
嘇
|
倁俛乮倁俼俛乯傪侾丏俈倁偵偡傞偨傔偵丄俼俛偼丄
|
俉丏俆倠兌
|
|
嘊
|
揹尮揹埑偑侾俀倁偩偐傜丄倁俼俙偼丄
|
侾侽丏俁倁
|
|
嘋
|
俬俼俙偼丄
乮俬俛傪柍帇偟丄俬俼俛亖俬俼俙亖俀侽侽兪俙偲偟偰傕椙偄乯
|
俀侾侽兪俙
|
|
嘍
|
俼俙偼丄
乮俬俼俛亖俬俼俙亖俀侽侽兪俙偲偟偨応崌偼丄俆俀倠兌乯
|
係俋倠兌
|
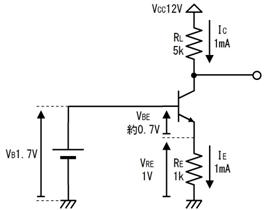
楙廗偱庢傝忋偘偨忋恾偺夞楬偱丄儀乕僗揹埑倁俛乮忋恾偱偼侾丏俈倁乯傪條乆偵曄壔偝偣偰丄奺晹偺偺揹埑傪應掕偡傞偲丄壓恾偺傛偆偵曄壔偟傑偡丅偙偺僌儔僼偼丄僌儔僼偺忋偵懳墳偡傞晹昳傪彂偒壛偊傞偲暘傝堈偔側傝傑偡丅
儀乕僗揹埑乮僌儔僼忋偺揰慄乯傪崅偔偡傞偲俬俠偑憹壛偟偰丄倁俠俤偑彫偝偔側傝丄夞楬偼僌儔僼忋傪塃偵堏摦偟傑偡丅儀乕僗揹埑偑俀丏俈倁偵側傞偲乮僐儗僋僞揹棳偑俀倣俙偵側傞偲乯倁俠俤偑侽倁偵側傝丄僩儔儞僕僗僞偼僔儑乕僩偟偨忬懺偵側傝傑偡丅偙偺忬懺傪俷俶忬懺乮朞榓忬懺乯偲屇傃傑偡丅
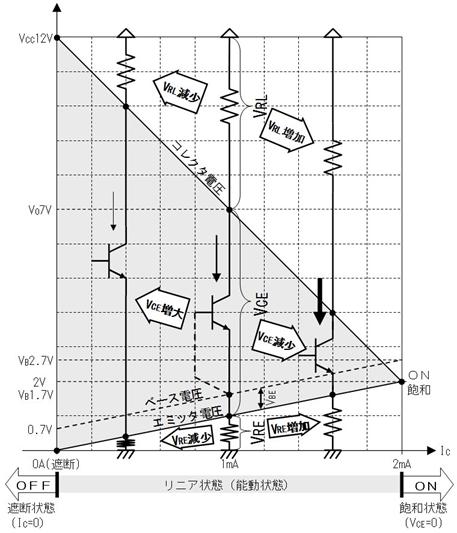
媡偵丄儀乕僗揹埑乮僌儔僼忋偺揰慄乯傪掅偔偡傞偲俬俠偑尭彮偟偰丄倁俠俤偑戝偒偔側傝丄夞楬偼僌儔僼忋傪嵍偵堏摦偟傑偡丅儀乕僗揹埑偑侽丏俈倁偵側傞偲俬俠偑侽倁偵側傝丄僩儔儞僕僗僞偼揹棳傪棳偝側偄忬懺偵側傝傑偡丅偙偺忬懺傪俷俥俥忬懺乮幷抐忬懺乯偲屇傃傑偡丅
俷俶偱傕俷俥俥偱傕側偄丄拞墰偺晹暘偑儕僯傾忬懺乮擻摦忬懺乯偱丄揹埑傗揹棳傪妸傜偐偵曄壔偝偣傞偙偲偑偱偒傑偡丅憹暆婍偵巊偆偺偼偙偺忬懺偱偡丅
侾. 庡側僩儔儞僕僗僞偺庬椶
師偺昞偵帵偡捠傝丄憹暆嶌梡偺偁傞敿摫懱偼杦偳乽乣僩儔儞僕僗僞乿偲屇偽傟傑偡丅偙傟傜僩儔儞僕僗僞懓偺拞偱傕丄堦斣嵟弶偵奐敪偝傟偨乽僶僀億乕儔丒僩儔儞僕僗僞乿偑丄擔杮偱偼扨偵乽僩儔儞僕僗僞乿偲屇偽傟傑偡丅杮彂偱傕扨偵乽僩儔儞僕僗僞乿偲屇傇応崌偼乽僶僀億乕儔丒僩儔儞僕僗僞乿傪巜偟傑偡丅
僩儔儞僕僗僞偺怓乆
|
僩儔儞僕僗僞偺庬椶
|
摢暥帤
|
傛偔偁傞屇傃曽
|
|
僶僀億乕儔丒僩儔儞僕僗僞
(偁傞偄偼)僶僀億乕儔丒僕儍儞僋僔儑儞丒僩儔儞僕僗僞
|
俛俰俿
|
僩儔儞僕僗僞
|
|
僕儍儞僋僔儑儞丒僼傿乕儖僪丒僄僼僃僋僩丒僩儔儞僕僗僞
|
俰俥俤俿
|
僄僼僀乕僥傿乕
|
|
儊僞儖丒僆僉僒僀僪丒僙儈僐儞僟僋僞乕丒僼傿乕儖僪
僄僼僃僋僩丒僩儔儞僕僗僞
|
俵俷俽俥俤俿
|
儌僗
儌僗僄僼僀亅僥傿乕
|
|
傾僀僜儗乕僥僢僪丒僎乕僩丒僶僀億乕儔丒僩儔儞僕僗僞
|
俬俧俛俿
|
傾僀僕乕價乕僥傿乕
|
徠柧傪揰摂乛徚摂偡傞摍丄揹棳傪乽棳偡乿乽棳偝側偄乿偩偗傪峴偊偽傛偄梡搑偑戲嶳偁傝傑偡丅偙偺傛偆側摦嶌傪僗僀僢僠儞僌偲屇傃傑偡丅
僗僀僢僠偱徠柧傪俷俶乛俷俥俥偟偰傕丄僗僀僢僠偑夁擬偟側偄傛偆偵丄僗僀僢僠儞僌偱摦嶌偡傞夞楬偼丄岠棪偑椙偔敪擬偑彮側偄偺偱丄懡梡偝傟傑偡丅
乽僩儔儞僕僗僞偺忬懺乿偱愢柧偟偨傛偆偵丄僩儔儞僕僗僞偵偼乽揹棳傪棳偝側偄俷俥俥忬懺乿偲丄倁俠俤偑侽倁偵側偭偰乽摫捠偡傞俷俶忬懺乿偑偁傝傑偡偐傜丄偙偺俀偮偺忬懺傪棙梡偡傟偽僗僀僢僠儞僌偑偱偒傑偡丅
壓恾乮倎乯偼晧壸乮揹媴乯偲捈楍偵僩儔儞僕僗僞傪愙懕偟偨僗僀僢僠儞僌夞楬偱偡丅傑偢僩儔儞僕僗僞傪俷俥俥偝偣偰丄揹媴傪徚摂偡傞曽朄傪峫偊傑偡丅
壓恾乮倎乯偺傛偆偵儀乕僗偵揹棳傪棳偝側偗傟偽丄僐儗僋僞偵傕揹棳偑棳傟偢丄僩儔儞僕僗僞偼俷俥俥偵側傞敜偱偡丅偲偙傠偑丄偙偺傑傑偱偼僩儔儞僕僗僞偼師偵傛偆偵摦嶌偟偰丄姰慡偵偼俷俥俥偵側傝傑偣傫丅
偮傑傝丄嘆僐儗僋僞偐傜儀乕僗偵岦偐偭偰嬐偐側俬俠俛俷偑乮楻傟偰乯棳傟傑偡丅儀乕僗偑偳偙偵傕愙懕偝傟偢偵曻抲偝傟偰偄傞偨傔丄嘇俬俠俛俷偼儀乕僗偐傜僄儈僢僞傊棳傟傑偡丅偙偙偱丄僩儔儞僕僗僞偼儀乕僗偵棳傟崬傫偩揹棳傪倛俥俤攞偟偰僐儗僋僞偵棳偟傑偡偐傜丄偨偲偊俬俠俛俷偑嬐偐侾兪俙偲嬐偐偱偁偭偰傕丄嘊僐儗僋僞偵偼侽丏侾倣俙偺揹棳偑棳傟偰偟傑偄傑偡丅
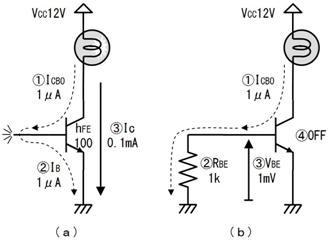
偦偙偱忋恾乮倐乯偺傛偆偵儀乕僗僄儈僢僞娫偵掞峈乮俼俛俤乯傪愙懕偟傑偡丅偦偆偡傟偽丄嘆僐儗僋僞偐傜儀乕僗偵岦偐偭偰俬俠俛俷偑侾兪俙棳傟偰棃偰傕丄嘇俼俛俤傪侾倠兌摍偲彫偝偔偡傟偽丄嘊俼俛俤偺椉抂偵偼乮僆乕儉懃偵傛傝乯倁俛俤偼侾倣倁偟偐敪惗偟傑偣傫丅揹棳偺棳傟傞僩儔儞僕僗僞偱偼倁俛俤偑侽丏俈倁掱搙敪惗偟傑偡偐傜丄偙偺傛偆偵倁俛俤偑侾倣倁偲彫偝偗傟偽丄嘋僩儔儞僕僗僞傪姰慡偵俷俥俥偡傞偙偲偑偱偒傑偡丅
偮傑傝丄忋恾乮倐乯偺傛偆偵丄俼俛俤傪愙懕偟丄俬俠俛俷偱敪惗偡傞揹埑傪侾倣倁掱搙偵彫偝偔偡傞傛偆偵抣傪慖傋偽丄僩儔儞僕僗僞傪俷俥俥偱偒傑偡丅
俁.侾. 楙廗
壓昞偺僨乕僞僔乕僩偺敳悎傪嶲峫偵丄壓恾偺夞楬偑姰慡偵俷俥俥偡傞傛偆偵丄壓昞偵彂偒崬傒側偑傜俼俛俤偺抣傪寛掕偟偰偔偩偝偄丅
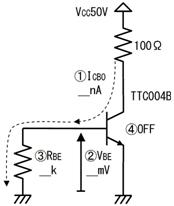
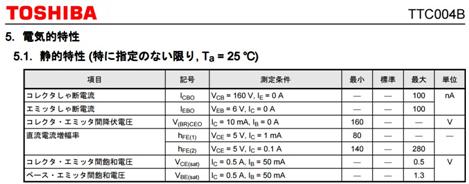
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僨乕僞僔乕僩傛傝丄俬俠俛俷偺抣偼丄
|
値俙
|
|
嘇
|
僩儔儞僕僗僞傪姰慡偵俷俥俥偝偣傞偨傔偵偼丄倁俛俤偼丄
|
倣倁埲壓
|
|
嘊
|
俬俠俛俷偑棳傟偰傕丄倁俛俤傪廫暘掅偔曐偮偵偼丄
|
倠兌
|
俁.俀. 摎
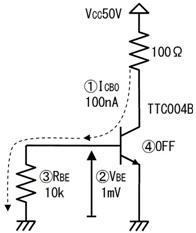
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僨乕僞僔乕僩傛傝丄俬俠俛俷偺抣偼丄
|
侾侽侽値俙
|
|
嘇
|
僩儔儞僕僗僞傪姰慡偵俷俥俥偝偣傞偨傔偵偼丄倁俛俤偼丄
|
侾倣倁埲壓
|
|
嘊
|
俬俠俛俷偑棳傟偰傕丄倁俛俤傪廫暘掅偔曐偮偵偼丄
侾倣倁亐侾侽侽値俙亖侾侽倠兌
|
侾侽倠兌
|
俬俠俛俷偑彫偝偗傟偽丄俼俛俤傪戝偒偔偡傞乮柍懯側徚旓揹棳傪尭傜偡乯偙偲偑偱偒傑偡丅戝揹棳傪棳偡偙偲偺偱偒傞戝宆偺僩儔儞僕僗僞傗丄愝寁偺屆偄僩儔儞僕僗僞偼丄俬俠俛俷偑戝偒偔側傞孹岦偑偁傝傑偡丅
僩儔儞僕僗僞傪俷俥俥偝偣傞乮俼俛俤傪庢傝晅偗偨乯夞楬偵丄壓恾偺傛偆偵僗僀僢僠偲俼俛傪捛壛偡傟偽丄僗僀僢僠傪墴偡偙偲偱乮儀乕僗偵揹棳偑棳傟偰乯僩儔儞僕僗僞傪俷俶偡傞夞楬傪嶌傞偙偲偑偱偒傑偡丅傑偢丄僩儔儞僕僗僞偑俷俶偟偰偄傞偲偒偺丄僐儗僋僞揹棳傪媮傔傑偡丅
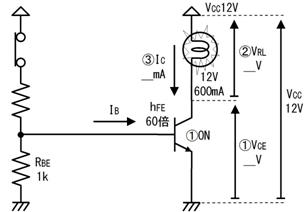
係.侾. 楙廗
忋恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜僐儗僋僞揹棳傪媮傔偰壓偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹媴傪揰摂偡傞偨傔偵丄僩儔儞僕僗僞偼俷俶偟偰偄傑偡丅
|
亅
|
|
嘇
|
俷俶偟偰偄傞僩儔儞僕僗僞偺倁俠俤偼丄
|
倁
|
|
嘊
|
揹尮揹埑偑侾俀倁偱偡偐傜丄晧壸乮揹媴乯偵壛傢傞揹埑偼丄
|
倁
|
|
嘋
|
揹媴偺巇條偐傜丄僐儗僋僞揹棳偼丄
|
倣俙
|
係.俀. 摎
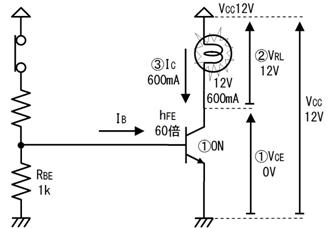
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹媴傪揰摂偡傞偨傔偵丄僩儔儞僕僗僞偼俷俶偟偰偄傑偡丅
|
亅
|
|
嘇
|
俷俶偟偰偄傞僩儔儞僕僗僞偺倁俠俤偼丄
|
侽倁
|
|
嘊
|
揹尮揹埑偑侾俀倁偱偡偐傜丄晧壸乮揹媴乯偵壛傢傞揹埑偼丄
|
侾俀倁
|
|
嘋
|
揹媴偺巇條偐傜丄僐儗僋僞揹棳偼丄
|
俇侽侽倣俙
|
偙偺傛偆偵僩儔儞僕僗僞偑俷俶偡傞偲丄僐儗僋僞偵偼俇侽侽倣俙偺揹棳偑棳傟傑偡丅
偝偰丄僐儗僋僞偵俇侽侽倣俙棳偡偨傔偵偼丄乮壖偵倛俥俤傪俇侽偲偡傟偽乯儀乕僗偵偼侾侽倣俙棳偣偽傛偄敜偱偡丅偲偙傠偑丄僩儔儞僕僗僞偑俷俶偡傞偲倛俥俤偑掅壓偡傞偨傔丄幚嵺偵偼儀乕僗偵俁侽倣俙棳偡昁梫偑偁傝傑偡丅
偱偼僩儔儞僕僗僞偺摿惈恾傪巊偭偰乽倛俥俤偺掅壓乿傪愢柧偟傑偡丅壓恾偼僩儔儞僕僗僞偺倁俠俤亅俬俠摿惈偺堦椺偱偡乮俬俛偑侾侽倣俙偺応崌偵拲栚偟偰偄傑偡乯丅僌儔僼偺嵍抂偑丄倁俠俤偑侽倁偲側傝僩儔儞僕僗僞偑俷俶偵側傞揰偱偡丅
傕偟倛俥俤偑倁俠俤偵娭學側偔乮椺偊偽俇侽攞偱乯堦掕偱偁傟偽丄俬俛偑侾侽倣俙側傜丄俬俠偼忢偵俇侽侽倣俙棳傟偰僌儔僼偼悈暯偲側傞敜偱偡丅妋偐偵倁俠俤偑侽丏俆倁埲忋偱偁傟偽丄僌儔僼拞墰偐傜塃懁偱尒傜傟傞傛偆偵丄僐儗僋僞揹棳偼俇侽侽倣俙偱傎傏堦掕偱悈暯偱偡丅
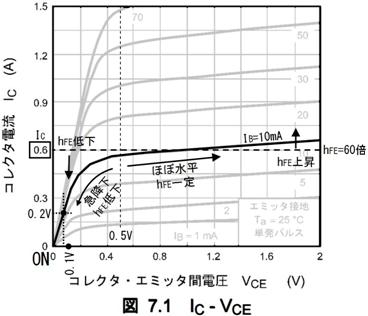
搶幣惢俿俿俠侽侽俁俛
偲偙傠偑丄倁俠俤偑侽丏俆倁傛傝掅偔側傞偲丄僌儔僼偺嵍抂偱尒傜傟傞傛偆偵丄倛俥俤偑掅壓偟俬俠偑媫掅壓偟傑偡丅偮傑傝丄僩儔儞僕僗僞偑俷俶偵嬤偯偔偲倛俥俤偑掅壓偟傑偡丅
偙偙偱僩儔儞僕僗僞傪廫暘偵俷俶偵偡傞曽朄傪峫偊傑偡丅忋恾偺僌儔僼偱丄僩儔儞僕僗僞偑廫暘偵俷俶偵側傝丄倁俠俤偑侽丏侾倁埲壓偵掅壓偡傞揰傪挷傋傞偲丄俬俛偼摨偠偔侾侽倣俙棳偟偰偄傞偺偵丄俬俠偑俀侽侽倣俙偵尭彮偟丄倛俥俤偼嵟弶偺栺俁暘偺侾偺俀侽攞掱搙傑偱掅壓偟偰偄傑偡丅偱偡偐傜丄僩儔儞僕僗僞偑俷俶偵側傟偽丄倛俥俤偼栺俁暘偺侾偵掅壓偡傞偲峫偊偰丄偦偺暘懡傔偵俁攞偺儀乕僗揹棳傪棳偣偽丄僩儔儞僕僗僞傪俷俶偵偱偒傑偡丅
偙偺傛偆偵丄僗僀僢僠儞僌夞楬偱偼儀乕僗揹棳傪懡傔偵棳偡昁梫偑偁傝傑偡丅懡傔偵棳偡妱崌乮捠忢俁攞掱搙乯傪乽僆乕僶乕僪儔僀僽乿偲屇傃傑偡丅
傑偨丄倛俥俤偵偼屄懱嵎偑偁傞偺偱丄儀乕僗揹棳偑晄懌偟側偄傛偆偵丄乮巊梡偡傞儔儞僋偺乯倛俥俤偺嵟彫抣傪巊偭偰寁嶼偟傑偡丅偨偲偊偽丄侾俀侽乣俀係侽攞偱偁傟偽丄侾俀侽攞偲偟偰寁嶼偟傑偡丅
偙偙傑偱愢柧偟偨乽俷俥俥偺曽朄乿乽俷俶偺曽朄乿傪傑偲傔傞偲丄僩儔儞僕僗僞偵傛傞僗僀僢僠儞僌夞楬偱偼丄師昞偺億僀儞僩偵拲堄偟偰専摙偡傟偽椙偄偲暘偐傝傑偡丅
|
忬懺
|
俷俥俥偝偣傞
|
俷俶偝偣傞
|
|
専摙偺
億僀儞僩
|
俬俠俛俷傪庴偗巭傔傞夞楬傪愝偗偰丄倁俛俤傪侾倣倁掱搙偵掅偔偡傞丅
|
俬俠亐倛俥俤偺抣偵僆乕僶乕僪儔僀僽乮栺俁攞乯傪妡偗偰俬俛傪媮傔傞丅
|
|
俬俛偑晄懌偟側偄傛偆偵丄寁嶼偵偼
倛俥俤偺嵟彫抣傪巊梡偡傞丅
|
|
嬶懱椺
|
俼俛俤傪庢傝晅偗傞丅
俬俠俛俷偑侾兪俙側傜丄俼俛俤偼侾倠兌掱搙
|
俬俛亖俁亊俬俠乛倛俥俤乮嵟掅乯
|
俷俥俥偝偣傞嬶懱揑側曽朄偼丄忋昞埲奜偵傕偄偔偮偐偁傝傑偡丅
俆.侾. 楙廗
壓昞偵彂偒崬傒側偑傜丄僩儔儞僕僗僞偑俷俶偵側傞偲倛俥俤偑俁暘偺侾偵尭彮偡傞偲峫偊丄儀乕僗揹棳傪俁攞棳偡乮俁攞偺僆乕僶乕僪儔僀僽傪偡傞乯傛偆丄壓恾偺夞楬傪専摙偟偰壓偝偄丅
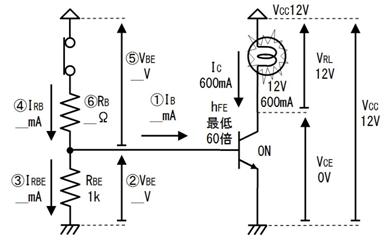
|
斣崋
|
幙栤
|
抣
|
|
|
揹媴偺巇條偱僐儗僋僞揹棳偼丄俇侽侽倣俙棳傟傑偡丅
|
亅
|
|
嘆
|
僩儔儞僕僗僞偑俷俶偵側傞偲倛俥俤偑俁暘偺侾偵尭彮偟丄儀乕僗揹棳偼俁攞昁梫偩偐傜丄儀乕僗揹棳偼丄
|
倣俙
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘊
|
乮僆乕儉懃傛傝乯俼俛俤偵棳傟傞揹棳俬俼俛俤偼丄
|
倣俙
|
|
嘋
|
乮僉儖僸懃傛傝乯俼俛偵棳傟傞揹棳俬俼俛偼丄
|
倣俙
|
|
嘍
|
俼俛偵壛傢傞揹埑偼丄
|
倁
|
|
嘐
|
俼俛偺抣偼丄
|
兌
|
俆.俀. 摎
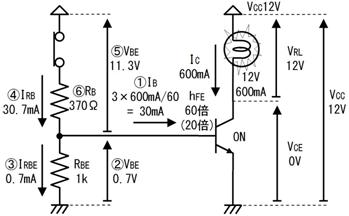
|
斣崋
|
幙栤
|
抣
|
|
|
揹媴偺巇條偱僐儗僋僞揹棳偼丄俇侽侽倣俙棳傟傑偡丅
|
亅
|
|
嘆
|
僩儔儞僕僗僞偑俷俶偵側傞偲倛俥俤偑俁暘偺侾偵尭彮偟丄儀乕僗揹棳偼俁攞昁梫偩偐傜丄儀乕僗揹棳偼丄
俇侽侽倣俙亐俇侽攞亊僆乕僶乕僪儔僀僽俁攞
|
俁侽倣俙
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘊
|
乮僆乕儉懃傛傝乯俼俛俤偵棳傟傞揹棳俬俼俛俤偼丄
|
侽丏俈倣俙
|
|
嘋
|
乮僉儖僸懃傛傝乯俼俛偵棳傟傞揹棳俬俼俛偼丄
|
俁侽丏俈倣俙
|
|
嘍
|
俼俛偵壛傢傞揹埑偼丄
|
侾侾丏俁倁
|
|
嘐
|
俼俛偺抣偼丄
|
俁俈侽兌
|
揹媴傪晧壸偵巊梡偡傞夞楬偱偼丄揰摂偡傞弖娫偩偗掕奿偺悢攞乣侾侽攞偺揹棳偑棳傟傞偨傔丄偙傟傪尒墇偟偨愝寁傪峴偄傑偡丅乮崱夞偼峴偭偰偄傑偣傫乯
俆.俁. 楙廗
壓恾偼僗僀僢僠傪俷俶偵偡傞偲俴俤俢偑揰摂偟丄俷俥俥偵偡傞偲徚摂偡傞夞楬偱偡丅
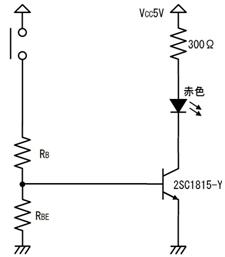
忋恾偺夞楬偺俼俛俤偲俼俛傪丄壓恾嵍乮俷俥俥偺応崌乯偲壓恾塃乮俷俶偺応崌乯傗丄壓偺僨乕僞僔乕僩傪嶲峫偵壓昞偵婰擖偟偰寛掕偟偰偔偩偝偄丅
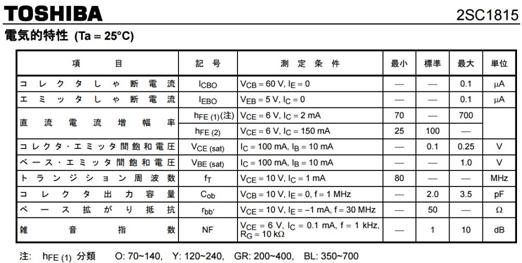
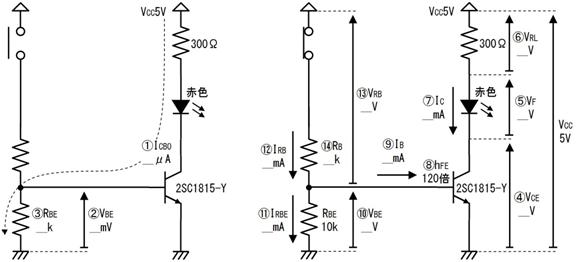
|
斣崋
|
幙栤
|
抣
|
|
|
僩儔儞僕僗僞偑俷俥俥偺応崌傪峫偊傑偡丅
|
亅
|
|
嘆
|
僨乕僞僔乕僩傛傝俬俠俛俷偼丄
|
兪俙
|
|
嘇
|
僩儔儞僕僗僞傪姰慡偵俷俥俥偡傞偨傔偵偼丄倁俛俤偼丄
|
倣倁埲壓
|
|
嘊
|
倁俛俤傪彫偝偔偡傞偨傔偵丄俼俛俤偼丄
|
倠兌
|
|
|
僩儔儞僕僗僞偑俷俶偺応崌傪峫偊傑偡丅
|
亅
|
|
嘋
|
俷俶偵側偭偨僩儔儞僕僗僞偺倁俠俤偼丄
|
倁
|
|
嘍
|
愒怓俴俤俢偺倁俥偼俀倁偲峫偊傑偡丅
|
俀倁
|
|
嘐
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
倁
|
|
嘑
|
乮僆乕儉懃傛傝乯僐儗僋僞揹棳偼丄
|
倣俙
|
|
嘒
|
僨乕僞僔乕僩壓晹傛傝乮暘椶倄偺乯倛俥俤偺嵟掅抣偼丄
|
攞
|
|
嘓
|
僆乕僶乕僪儔僀僽傪俁攞偲偡傞偲丄俬俛偼丄
俁亊侾侽倣俙亐侾俀侽亖侽丏俀俆倣俙
|
倣俙
|
|
嘔
|
揹棳傪棳偟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘕
|
俼俛俤偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘖
|
僉儖僸懃傛傝丄俼俛偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘗
|
俼俛偺椉抂揹埑偼丄
|
倁
|
|
嘙
|
俼俛偺抣偼丄
|
倠兌
|
俆.係. 摎
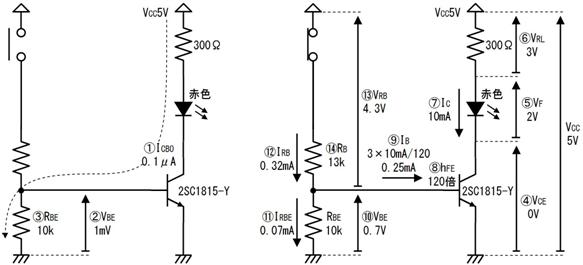
|
斣崋
|
幙栤
|
抣
|
|
|
僩儔儞僕僗僞偑俷俥俥偺応崌傪峫偊傑偡丅
|
亅
|
|
嘆
|
僨乕僞僔乕僩傛傝俬俠俛俷偼丄
|
侽丏侾兪俙
|
|
嘇
|
僩儔儞僕僗僞傪姰慡偵俷俥俥偡傞偨傔偵偼丄倁俛俤偼丄
|
侾倣倁埲壓
|
|
嘊
|
倁俛俤傪彫偝偔偡傞偨傔偵丄俼俛俤偼丄
|
侾侽倠兌
|
|
|
僩儔儞僕僗僞偑俷俶偺応崌傪峫偊傑偡丅
|
亅
|
|
嘋
|
俷俶偵側偭偨僩儔儞僕僗僞偺倁俠俤偼丄
|
侽倁
|
|
嘍
|
愒怓俴俤俢偺倁俥偼俀倁偲峫偊傑偡丅
|
俀倁
|
|
嘐
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
俁倁
|
|
嘑
|
乮僆乕儉懃傛傝乯僐儗僋僞揹棳偼丄
|
侾侽倣俙
|
|
嘒
|
僨乕僞僔乕僩傛傝乮暘椶倄偺乯倛俥俤偺嵟掅抣偼丄
|
侾俀侽攞
|
|
嘓
|
僆乕僶乕僪儔僀僽傪俁攞偲偡傞偲丄俬俛偼丄
俁亊侾侽倣俙亐侾俀侽亖侽丏俀俆倣俙
|
侽丏俀俆倣俙
|
|
嘔
|
揹棳傪棳偟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘕
|
俼俛俤偵棳傟傞揹棳偼丄
|
侽丏侽俈倣俙
|
|
嘖
|
僉儖僸懃傛傝丄俼俛偵棳傟傞揹棳偼丄
|
侽丏俁俀倣俙
|
|
嘗
|
俼俛偺椉抂揹埑偼丄
|
係丏俁倁
|
|
嘙
|
俼俛偺抣偼丄
|
侾俁倠兌
|
俆.俆. 楙廗
壓恾偼僗僀僢僠偺俷俶偵側傞偲俴俤俢偑徚摂偟丄俷俥俥偵側傞偲揰摂偡傞夞楬偱偡丅
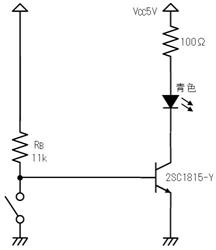
忋恾偺夞楬偺俼俛傪丄壓恾嵍懁乮俷俥俥偺偲偒乯偲壓恾塃懁乮俷俶偺偲偒乯傗丄婛嵹偺僨乕僞僔乕僩傪嶲峫偵壓昞偵婰擖偟偰寛掕偟偰偔偩偝偄丅
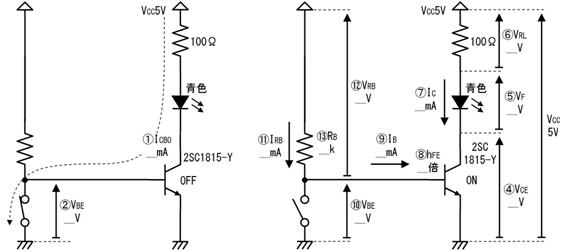
|
斣崋
|
幙栤
|
抣
|
|
|
僩儔儞僕僗僞偑俷俥俥偺応崌傪峫偊傑偡丅
|
亅
|
|
嘆
|
僨乕僞僔乕僩傛傝俬俠俛俷偼丄
|
兪俙
|
|
嘇
|
僗僀僢僠偑俷俶側傜倁俛俤偼丄
|
倁
|
|
嘊
|
僩儔儞僕僗僞偼丄乮慖傫偱壓偝偄乯
|
俷俶丒俷俥俥
|
|
|
僩儔儞僕僗僞偑俷俶偺応崌傪峫偊傑偡丅
|
亅
|
|
嘋
|
俷俶偵側偭偨僩儔儞僕僗僞偺倁俠俤偼丄
|
倁
|
|
嘍
|
惵怓俴俤俢偺倁俥偼俁丏俆倁偲峫偊傑偡丅
|
倁
|
|
嘐
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
倁
|
|
嘑
|
乮僆乕儉懃傛傝乯僐儗僋僞揹棳偼丄
|
倣俙
|
|
嘒
|
僨乕僞僔乕僩傛傝乮暘椶倄偺乯倛俥俤偺嵟掅抣偼丄
|
攞
|
|
嘓
|
僆乕僶乕僪儔僀僽傪俁攞偲偡傞偲丄俬俛偼丄
俁亊侾俆倣俙亐侾俀侽亖侽丏俀俆倣俙
|
倣俙
|
|
嘔
|
揹棳傪棳偟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘕
|
俼俛偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘖
|
俼俛偺椉抂揹埑偼丄
|
倁
|
|
嘗
|
俼俛偺抣偼丄
|
倠兌
|
俆.俇. 摎
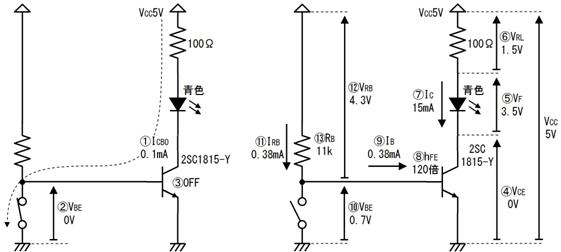
|
斣崋
|
幙栤
|
抣
|
|
|
僩儔儞僕僗僞偑俷俥俥偺応崌傪峫偊傑偡丅
|
亅
|
|
嘆
|
僨乕僞僔乕僩傛傝俬俠俛俷偼丄
|
侽丏侾兪俙
|
|
嘇
|
僗僀僢僠偑俷俶側傜倁俛俤偼丄
|
侽倁
|
|
嘊
|
僩儔儞僕僗僞偼丄乮慖傫偱壓偝偄乯
|
俷俶丒俷俥俥
|
|
|
僩儔儞僕僗僞偑俷俶偺応崌傪峫偊傑偡丅
|
亅
|
|
嘋
|
俷俶偵側偭偨僩儔儞僕僗僞偺倁俠俤偼丄
|
侽倁
|
|
嘍
|
惵怓俴俤俢偺倁俥偼俁丏俆倁偲峫偊傑偡丅
|
俁丏俆倁
|
|
嘐
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
侾丏俆倁
|
|
嘑
|
乮僆乕儉懃傛傝乯僐儗僋僞揹棳偼丄
|
侾俆倣俙
|
|
嘒
|
僨乕僞僔乕僩傛傝乮暘椶倄偺乯倛俥俤偺嵟掅抣偼丄
|
侾俀侽攞
|
|
嘓
|
僆乕僶乕僪儔僀僽傪俁攞偲偡傞偲丄俬俛偼丄
俁亊侾俆倣俙亐侾俀侽亖侽丏俀俆倣俙
|
侽丏俁俉倣俙
|
|
嘔
|
揹棳傪棳偟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘕
|
俼俛偵棳傟傞揹棳偼丄
|
侽丏俁俉倣俙
|
|
嘖
|
俼俛偺椉抂揹埑偼丄
|
係丏俁倁
|
|
嘗
|
俼俛偺抣偼丄
|
侾俁倠兌
|
偙偺傛偆偵丄僩儔儞僕僗僞傪俷俥俥偝偣傞偲偒丄俼俛俤偺戙傢傝偵俬俠俛俷偑棳傟傞宱楬偑偁傞夞楬偱偼丄俼俛俤偑晄梫偱偡丅
俆.俈. 楙廗
壓恾偼僗僀僢僠傪愗傝懼偊偰丄儕儗乕傪俷俶乛俷俥俥偡傞夞楬偱偡丅儕儗乕偲暲楍偵愙懕偟偨僟僀僆乕僪偼丄師偺崁偱愢柧偡傞丄僼儔僀僶僢僋揹埑偺媧廂梡偱偡丅
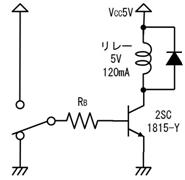
忋恾偺夞楬偺俼俛傪丄壓恾嵍懁乮俷俥俥偺偲偒乯偲壓恾塃懁乮俷俶偺偲偒乯傗丄婛嵹偺僨乕僞僔乕僩傪嶲峫偵壓昞偵婰擖偟偰寛掕偟偰偔偩偝偄丅
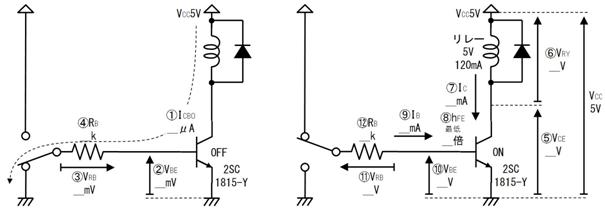
|
斣崋
|
幙栤
|
抣
|
|
|
僩儔儞僕僗僞偑俷俥俥偺応崌傪峫偊傑偡丅
|
亅
|
|
嘆
|
僨乕僞僔乕僩傛傝丄俬俠俛俷偼丄
|
兪俙
|
|
嘇
|
僩儔儞僕僗僞傪姰慡偵俷俥俥偡傞偨傔偵偼丄倁俛俤偼丄
|
倣倁埲壓
|
|
嘊
|
俼俛偺椉抂揹埑倁俼俛偼丄
|
倣倁埲壓
|
|
嘋
|
俼俛偺抣偼丄
|
倠兌埲壓
|
|
|
僩儔儞僕僗僞偑俷俶偺応崌傪峫偊傑偡丅
|
|
|
嘍
|
俷俶偵側偭偨僩儔儞僕僗僞偺倁俠俤偼丄
|
倁
|
|
嘐
|
儕儗乕偺椉抂揹埑倁俼倄偼丄
|
倁
|
|
嘑
|
儕儗乕偺巇條偐傜丄僐儗僋僞揹棳偼丄
|
倣俙
|
|
嘒
|
僨乕僞僔乕僩偐傜丄乮倄暘椶偺乯倛俥俤偺嵟掅抣偼丄
|
攞
|
|
嘓
|
僆乕僶乕僪儔僀僽傪俁攞埲忋偲偡傞偲丄俬俛偼丄
|
倣俙埲忋
|
|
嘔
|
揹棳偑棳傟傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘕
|
俼俛偺椉抂揹埑倁俼俛偼丄
|
倁
|
|
嘖
|
俼俛偺抣偼丄
|
倠兌埲壓
|
|
嘗
|
忋偺嘋偲嘖偺憃曽傪枮懌偡傞俼俛偺抣偼丄
|
倠兌
|
俆.俉. 摎
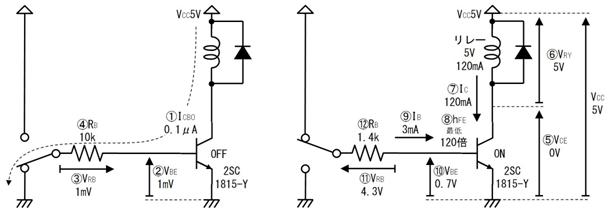
|
斣崋
|
幙栤
|
抣
|
|
|
僩儔儞僕僗僞偑俷俥俥偺応崌傪峫偊傑偡丅
|
亅
|
|
嘆
|
僨乕僞僔乕僩傛傝丄俬俠俛俷偼丄
|
侽丏侾兪俙
|
|
嘇
|
僩儔儞僕僗僞傪姰慡偵俷俥俥偡傞偨傔偵偼丄倁俛俤偼丄
|
侾倣倁埲壓
|
|
嘊
|
俼俛偺椉抂揹埑倁俼俛偼丄
|
侾倣倁埲壓
|
|
嘋
|
俼俛偺抣偼丄
|
侾侽倠兌埲壓
|
|
|
僩儔儞僕僗僞偑俷俶偺応崌傪峫偊傑偡丅
|
|
|
嘍
|
俷俶偵側偭偨僩儔儞僕僗僞偺倁俠俤偼丄
|
侽倁
|
|
嘐
|
儕儗乕偺椉抂揹埑倁俼倄偼丄
|
俆倁
|
|
嘑
|
儕儗乕偺巇條偐傜丄僐儗僋僞揹棳偼丄
|
侾俀侽倣俙
|
|
嘒
|
僨乕僞僔乕僩偐傜丄乮倄暘椶偺乯倛俥俤偺嵟掅抣偼丄
|
侾俀侽攞
|
|
嘓
|
僆乕僶乕僪儔僀僽傪俁攞埲忋偲偡傞偲丄俬俛偼丄
|
俁倣俙埲忋
|
|
嘔
|
揹棳偑棳傟傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘕
|
俼俛偺椉抂揹埑倁俼俛偼丄
|
係丏俁倁
|
|
嘖
|
俼俛偺抣偼丄
|
侾丏係倠兌埲壓
|
|
嘗
|
忋偺嘋偲嘖偺憃曽傪枮懌偡傞俼俛偺抣偼丄
|
侾丏係倠兌
|
偙偺傛偆偵丄堦杮偺掞峈偑俼俛俤偲俼俛憃曽偺栶妱傪壥偨偡応崌偼丄憃曽偺忦審偵崌偆掞峈抣傪慖傃傑偡丅
偙偺僞僀僾偺夞楬偼丄壓恾偺傛偆偵丄儅僀僐儞摍偺俠俵俷俽僨僕僞儖弌椡乮忋偺楙廗偺椺偱偼弌椡揹棳俁倣俙埲忋偺僞僀僾偑昁梫乯偱僩儔儞僕僗僞傪俷俶乛俷俥俥偡傞応崌偵棙梡偱偒傑偡丅
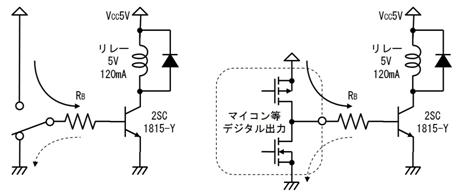
忋偺楙廗偱庢傝忋偘偨儕儗乕偺傛偆側僐僀儖惉暘傪帩偭偨晧壸傪乽桿摫晧壸乿偲屇傃傑偡丅桿摫晧壸偱偼丄乽僼儔僀僶僢僋乿偺崁偱愢柧偟偨傛偆偵丄俷俥俥帪偵崅偄揹埑偑惗偠偰僩儔儞僕僗僞傪攋夡偟傑偡丅
壓恾偼僼儔僀僶僢僋揹埑偺堦椺偱丄俆兪俫偺僐僀儖傪晧壸偵愙懕偟偰丄僩儔儞僕僗僞傪俆兪昩娫俷俶偵偟偨屻丄僌儔僼忋偺俇兪昩偺帪揰偱俷俥俥偵偟偰偄傑偡丅揹尮揹埑偼侾俀倁偱偡偑丄堦弖俇侽侽侽倁掱搙偺僼儔僀僶僢僋揹埑偑敪惗偟偰偄傑偡丅
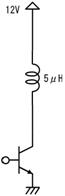 丂丂丂丂丂丂
丂丂丂丂丂丂
偙偺僼儔僀僶僢僋揹埑傪梷偊傞偨傔偵丄僼儔僀僶僢僋揹棳傪媧廂偡傞僗僫僶夞楬傪捛壛偟傑偡丅
壓恾偼慜崁偱棙梡偟偨僟僀僆乕僪傪巊梡偟偨僗僫僶夞楬偱偡丅偙偺夞楬偼壓恾偵崟慄偱帵偡傛偆偵丄僼儔僀僶僢僋揹埑傪姰慡偵梷偊傞偙偲偑偱偒傑偡丅偟偐偟丄僐僀儖偺揹棳偼奃怓慄偱帵偡傛偆偵備偭偔傝偲尭彮偡傞偨傔丄偡偽傗偔俷俶乛俷俥俥傪孞傝曉偡偙偲偑偱偒傑偣傫丅偙偺偨傔丄昩扨埵偱備偭偔傝摦嶌偡傞儕儗乕傗僜儗僲僀僪乮揹帴愇乯偱棙梡偝傟傑偡丅
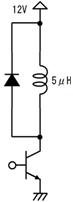 丂丂丂丂丂丂
丂丂丂丂丂丂
壓恾偵帵偡傛偆偵丄僟僀僆乕僪偲捈楍偵掞峈傪擖傟傞偙偲偱丄僼儔僀僶僢僋揹埑偼偐側傝敪惗偟傑偡偑丄乮掞峈偱僐僀儖偵拁偊傜傟偨僄僱儖僊偑擬偲側偭偰敪嶶偟乯揹棳偑慺憗偔尭彮偡傞傛偆偵側傝傑偡丅
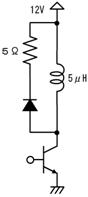 丂丂丂丂丂
丂丂丂丂丂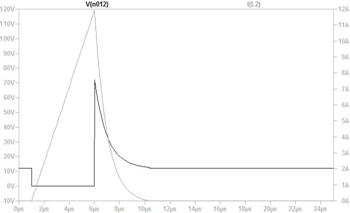
壓恾偵帵偡傛偆偵丄掞峈偲暲楍偵僐儞僨儞僒傪擖傟傞偲丄僼儔僀僶僢僋揹棳偑僐儞僨儞僒偵媧廂偝傟丄僼儔僀僶僢僋揹埑傪偐側傝彫偝偔偱偒傑偡丅乮僐儞僨儞僒偵拁偊傜傟偨僐僀儖偺僄僱儖僊偼丄掞峈偱曻弌偝傟傑偡乯僼儔僀僶僢僋揹埑偑掅偔側傝丄僐僀儖偺揹棳傕斾妑揑慺憗偔尭彮偡傞偺偱丄僗僀僢僠儞僌揹尮摍偱傛偔棙梡偝傟傑偡丅
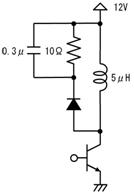 丂丂
丂丂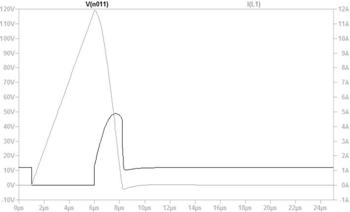
壓恾偵帵偡傛偆偵丄僩儔儞僕僗僞偲暲楍偵僣僃乕僫僟僀僆乕僪傪擖傟傞偲丄僼儔僀僶僢僋揹埑傪僣僃乕僫揹埑埲壓偵梷偊傞偙偲偑偱偒傑偡丅僣僃乕僫僟僀僆乕僪偼僼儔僀僶僢僋揹棳偵懴偊傞昳庬偑昁梫偱偡丅屻偱愢柧偡傞俵俷俽俥俤俿偵偼僣僃乕僫僟僀僆乕僪偲偟偰傕摦嶌偱偒傞昳庬乮傾僶儔儞僔僃懴検偺戝偒側昳庬乯傕偁傞偺偱丄偦偺傛偆側応崌偵棙梡偝傟傑偡丅
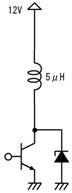 丂丂丂丂丂丂
丂丂丂丂丂丂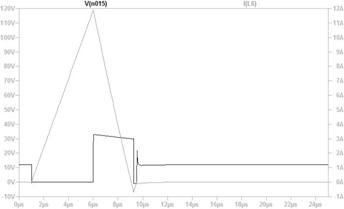
壓恾偼傛傝扨弮側俠俼偵傛傞僗僫僶夞楬偱偡丅僟僀僆乕僪偑晄梫偱偡偑僼儔僀僶僢僋揹埑偼偐側傝戝偒偔側傝傑偡丅
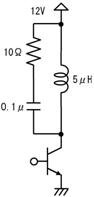 丂丂丂丂丂
丂丂丂丂丂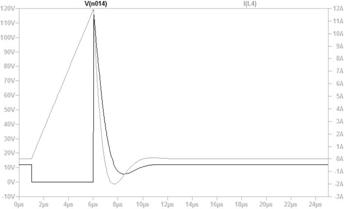
俶俹俶僩儔儞僕僗僞傪巊偭偨夞楬偼丄娙扨偵俹俶俹傪巊偭偨夞楬偵曄峏偱偒傑偡丅壓恾偼偡偱偵楙廗偱埖偭偨僗僀僢僠儞僌夞楬偱偡丅

忋恾偺夞楬偱偼俶俹俶僩儔儞僕僗僞傪巊偭偰偄傑偡丅夞楬恾偺忋壓傪媡偵偟偰丄揹棳偺岦偒傪媡曽岦偵偡傟偽丄俹俶俹僩儔儞僕僗僞偺夞楬偵側傝傑偡丅
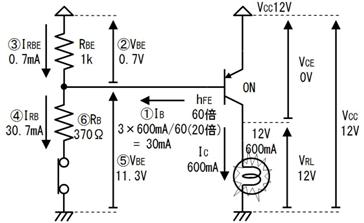
忋恾偺夞楬偱偼丄晧壸乮揹媴乯偺曅懁傪傾乕僗偵愙懕偡傞偙偲偑偱偒傞乮揹媴偑徚偊偰偄傟偽丄抂巕偵怗偭偰傕姶揹偟側偄乯偲偄偆棙揰偑偁傝傑偡丅
僗僀僢僠儞僌夞楬偱傕丄憹暆夞楬偱傕丄僩儔儞僕僗僞傪巊偭偨夞楬偱偁傟偽丄摨偠曽朄偱俶俹俶偲俹俶俹傪抲偒姺偊傞偙偲偑偱偒傑偡丅
俹俶俹僩儔儞僕僗僞偼儂乕儖乮嬻偺寠乯偑揹婥傪塣傇偨傔丄乮摦偒堈偄揹巕偑揹婥傪塣傇乯俶俹俶僩儔儞僕僗僞傛傝摦嶌偑抶偔側傞孹岦偑偁傝丄巊梡偝傟傞昿搙偼俶俹俶傛傝彮側偄偱偡丅偲偼偄偊丄俶俹俶偲俹俶俹傪慻傒崌傢偣偰妶梡偟偨夞楬傕偁傝丄俹俶俹僩儔儞僕僗僞偺弌斣傕姰慡偵偼柍偔側傝傑偣傫丅
壓恾偼丄俹俶俹僩儔儞僕僗僞偲俶俹俶僩儔儞僕僗僞傪慻傒崌傢偣偨丄俀抜偺僗僀僢僠儞僌夞楬偱偡丅夞楬傪擇抜偵偡傞偙偲偱丄嬌嬐偐側揹棳偱晧壸傪俷俶乛俷俥俥偱偒傑偡丅
俈.侾. 楙廗
壓恾傪嶲峫偵壓昞偵婰擖偟偰丄壓恾偺夞楬偺掞峈抣傪寛掕偟偰偔偩偝偄丅
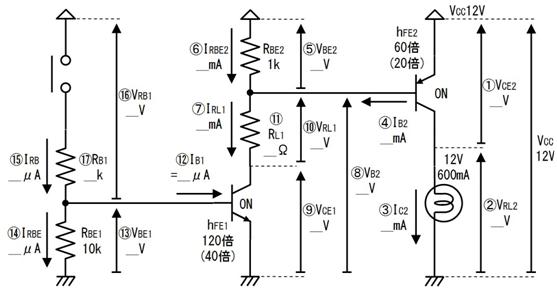
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俷俶偵側偭偰偄傞僩儔儞僕僗僞俻俀偺倁俠俤俀偼丄
|
倁
|
|
嘇
|
俻俀偺晧壸俼俴俀偺椉抂揹埑偼丄
|
倁
|
|
嘊
|
揹媴偺掕奿傛傝丄俻俀偺僐儗僋僞揹棳俬俠俀偼丄
|
倣俙
|
|
嘋
|
俁攞偺僆乕僶乕僪儔僀僽傪妡偗偰丄俻俀偺儀乕僗揹棳俬俛俀偼丄
|
倣俙
|
|
嘍
|
俻俀偺儀乕僗僄儈僢僞娫揹埑倁俛俤俀偼丄
|
倁
|
|
嘐
|
俼俛俤俀偵棳傟傞揹棳俬俼俛俤俀偼丄
|
倣俙
|
|
嘑
|
俻侾偺晧壸掞峈俼俴侾偵棳傟傞揹棳偼丄
乮嘐偲嘋傛傝僉儖僸懃偱乯
|
倣俙
|
|
嘒
|
俻俀偺儀乕僗揹埑倁俛俀偼丄
|
倁
|
|
嘓
|
俷俶偵側偭偰偄傞俻侾偺倁俠俤侾偼丄
|
倁
|
|
嘔
|
俻侾偺晧壸掞峈俼俴侾偺椉抂揹埑偼丄
|
倁
|
|
嘕
|
俻侾偺晧壸掞峈俼俴侾偺掞峈抣偼丄
|
兌
|
|
嘖
|
俁攞偺僆乕僶乕僪儔僀僽傪妡偗偰丄俻侾偺儀乕僗揹棳俬俛侾偼丄
|
兪俙
|
|
嘗
|
揹棳偺棳傟偰偄傞俻侾偺倁俛俤侾偼丄
|
倁
|
|
嘙
|
俻侾偺俼俛俤侾偵棳傟傞揹棳俬俼俛俤侾偼丄
|
兪俙
|
|
嘚
|
俻侾偺儀乕僗掞峈俼俛侾偵棳傟傞揹棳俬俼俛侾偼丄
乮嘗偲嘙傛傝僉儖僸懃偱乯
|
兪俙
|
|
嘜
|
俻侾偺儀乕僗掞峈俼俛侾偺掞峈抣偼丄
|
倠兌
|
俈.俀. 摎
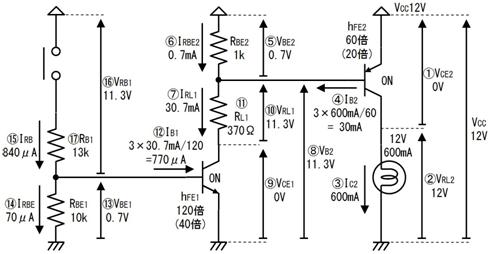
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俷俶偵側偭偰偄傞僩儔儞僕僗僞俻俀偺倁俠俤俀偼丄
|
侽倁
|
|
嘇
|
俻俀偺晧壸俼俴俀偺椉抂揹埑偼丄
|
侾俀倁
|
|
嘊
|
揹媴偺掕奿傛傝丄俻俀偺僐儗僋僞揹棳俬俠俀偼丄
|
俇侽侽倣俙
|
|
嘋
|
俁攞偺僆乕僶乕僪儔僀僽傪妡偗偰丄俻俀偺儀乕僗揹棳俬俛俀偼丄
|
俁侽倣俙
|
|
嘍
|
俻俀偺儀乕僗僄儈僢僞娫揹埑倁俛俤俀偼丄
|
侽丏俈倁
|
|
嘐
|
俼俛俤俀偵棳傟傞揹棳俬俼俛俤俀偼丄
|
侽丏俈倣俙
|
|
嘑
|
俻侾偺晧壸掞峈俼俴侾偵棳傟傞揹棳偼丄
乮嘐偲嘋傛傝僉儖僸懃偱乯
|
俁侽丏俈倣俙
|
|
嘒
|
俻俀偺儀乕僗揹埑倁俛俀偼丄
|
侾侾丏俁倁
|
|
嘓
|
俷俶偵側偭偰偄傞俻侾偺倁俠俤侾偼丄
|
侽倁
|
|
嘔
|
俻侾偺晧壸掞峈俼俴侾偺椉抂揹埑偼丄
|
侾侾丏俁倁
|
|
嘕
|
俻侾偺晧壸掞峈俼俴侾偺掞峈抣偼丄
|
俁俈侽兌
|
|
嘖
|
俁攞偺僆乕僶乕僪儔僀僽傪妡偗偰丄俻侾偺儀乕僗揹棳俬俛侾偼丄
|
俈俈侽兪俙
|
|
嘗
|
揹棳偺棳傟偰偄傞俻侾偺倁俛俤侾偼丄
|
侽丏俈倁
|
|
嘙
|
俻侾偺俼俛俤侾偵棳傟傞揹棳俬俼俛俤侾偼丄
|
俈侽兪俙
|
|
嘚
|
俻侾偺儀乕僗掞峈俼俛侾偵棳傟傞揹棳俬俼俛侾偼丄
乮嘗偲嘙傛傝僉儖僸懃偱乯
|
俉係侽兪俙
|
|
嘜
|
俻侾偺儀乕僗掞峈俼俛侾偺掞峈抣偼丄
|
侾俁倠兌
|
僗僀僢僠儞僌夞楬乮俷俶忬懺偲俷俥俥忬懺偱摦嶌偡傞乯偲偼堘偄丄儕僯傾夞楬偼儕僯傾忬懺乮擻摦忬懺乯偱摦嶌偡傞夞楬偱丄擖椡偺曄壔偵懳墳偟偰丄弌椡傕妸傜偐偵曄壔偟傑偡丅儕僯傾夞楬偵偼丄彫偝側怳暆傪埖偆彫怣崋憹暆夞楬偲丄戝偒側怳暆傪埖偆揹椡憹暆夞楬偑偁傝傑偡丅
彫怣崋憹暆夞楬偲偼丄壓恾乮倎乯偵帵偡傛偆偵丄夞楬偵壛傢傞捈棳揹埑乮僶僀傾僗揹埑乯偵斾傋偰丄岎棳揹埑乮怣崋揹埑乯偑廫暘偵彫偝偄夞楬偱偡丅偮傑傝怣崋偵傛偭偰夞楬偺揹埑偑曄壔偟偰傕丄捈棳揹埑偑憹尭偟偨偲峫偊傞昁梫偺柍偄乮掱偵彫偝側怣崋偟偐埖傢側偄乯夞楬偱偡丅彫怣崋憹暆夞楬偱偼丄捈棳偲岎棳傪乮僶僀傾僗偲怣崋傪乯傑偭偨偔暿乆偵寁嶼偟偰夞楬傪愝寁偡傞偙偲偑偱偒丄愝寁偑梕堈偵側傝傑偡丅
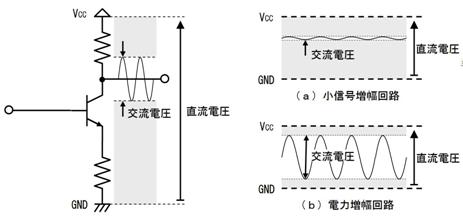
偲偙傠偑丄忋恾乮倐乯偺傛偆偵怣崋偑戝偒偔側傞偲丄怣崋偑戝偒偔怳傟偨晹暘偱偼夞楬偺揹埑偑曄壔偟偨偲峫偊偰寁嶼偡傞昁梫偑偁傝傑偡丅偙偺傛偆側夞楬偼揹椡憹暆夞楬偲屇偽傟傑偡丅婛偵愢柧偟偨僗僀僢僠儞僌夞楬偼揹椡憹暆夞楬偺堦偮偱偡丅
揹椡憹暆夞楬偱偼捈棳偲岎棳傪暿乆偵峫偊傞偙偲偼弌棃偢丄乽夞楬偺揹埑偑條乆偵曄壔偡傞乿偲峫偊偰愝寁偟傑偡丅僗僀僢僠儞僌夞楬偱乽俷俶偺応崌乿偲乽俷俥俥偺応崌乿傪暿乆偵峫偊偰愝寁偟偨偺傕偙偺偨傔偱偡丅
憹暆夞楬偵偼捈棳揹棳傗怣崋乮岎棳乯揹棳偑擖傝崿偠偭偰棳傟偰偄傞偨傔丄捈棳偲岎棳傪摨帪偵峫偊傞偲柺搢偱偡丅偟偐偟丄彫怣崋憹暆夞楬偱偼乽愭偵捈棳傪専摙偟偰丄屻偱岎棳傪専摙偡傞乿偲偄偆傛偆偵丄乮乽廳偹崌傢偣偺尨棟乿傪捈棳偲岎棳偵墳梡偟偰乯捈棳偲岎棳傪暿乆偵専摙偡傞偙偲偑偱偒傑偡丅
偨偲偊偽壓恾偺夞楬偱丄捈棳偩偗傪峫偊傞応崌偼丄壓恾忋懁偺傛偆偵丄岎棳揹尮傪摫慄偩偲峫偊傑偡丅傑偨丄僐儞僨儞僒偼捈棳傪棳偟傑偣傫偐傜乽晅偄偰側偄乿偲峫偊傑偡丅偦偆偡傞偲丄俀兌偑俀杮捈楍偲側傝丄侾俙偺捈棳偑棳傟傑偡丅
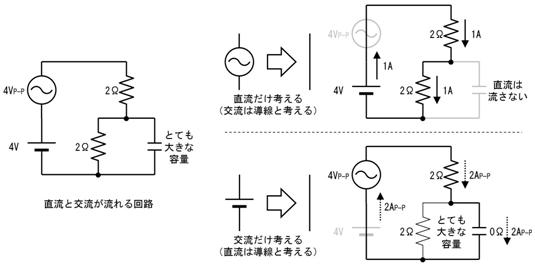
傑偨丄岎棳偩偗傪峫偊傞応崌偼丄忋恾壓懁偺傛偆偵丄捈棳揹尮乮揹抮乯傪摫慄偩偲峫偊傑偡丅傑偨丄廫暘戝偒側梕検偺僐儞僨儞僒偼侽兌偲峫偊傑偡丅偦偆偡傟偽丄俀兌偺掞峈偵俀俙偺揹棳偑棳傟傞偲暘傝傑偡丅
偙偺傛偆偵捈棳偲岎棳傪暿乆偵専摙偟偨寢壥傪崌傢偣傟偽丄夞楬偵棳傟傞捈棳偲岎棳傪壓恾偺傛偆偵抦傞偙偲偑偱偒傑偡丅暋嶨側憹暆夞楬偺摥偒傕丄梕堈偵専摙偡傞偙偲偑偱偒傑偡丅
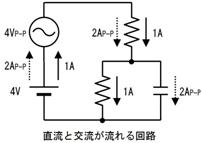
俋.侾. 楙廗
壓恾偺夞楬偺奺慺巕偵棳傟傞捈棳偲岎棳偺岦偒偲戝偒偝傪媮傔偰壓偝偄丅
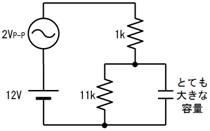
俋.俀. 摎
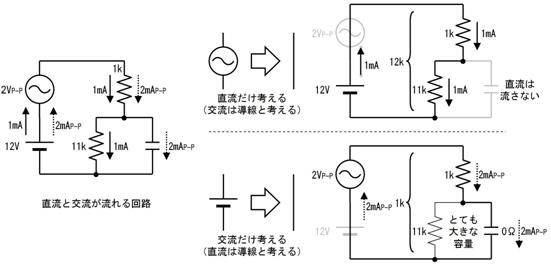
婛偵愢柧偟偨傛偆偵丄壓恾嵍懁偺夞楬偱僟僀僆乕僪偵壛偊傞揹埑倁俥傪曄偊傞偲丄棳傟傞揹棳俬俥偼丄椺偊偽丄壓恾塃懁偺摿惈恾偺傛偆偵曄壔偟傑偟偨丅乮偙偺摿惈恾偼Excel偱=1E-11*(EXP(E1/0.026)-1)傪寁嶼偟偰嶶晍恾偵昤偄偨傕偺偱偡丅乯
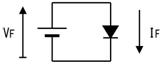 丂丂丂
丂丂丂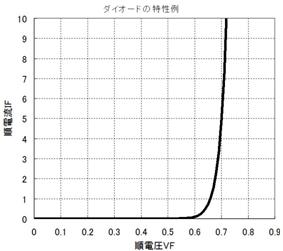
忋恾偐傜暘傞傛偆偵丄僟僀僆乕僪偼乮僆乕儉懃偵廬偭偰乯掞峈偺傛偆偵揹埑偲揹棳偑斾椺偟傑偣傫丅揹埑偑崅偔側傝丄揹棳偑憹偊傟偽憹偊傞掱丄揹棳偑棳傟堈偔側傝乮尒偐偗偺掞峈抣偑彫偝偔側傝乯丄嬐偐側揹埑偺憹壛偱揹棳偑戝偒偔憹偊傞傛偆偵側傝傑偡丅偙偺偨傔丄倁俥偑侽丏俈倁傪挻偊偨曈傝偐傜丄媫寖偵揹棳偑憹壛偟傑偡丅
師偵丄壓恾嵍懁偺夞楬偱僟僀僆乕僪偵捈棳偲岎棳傪摨帪偵壛偊偨応崌傪峫偊傑偡丅僟僀僆乕僪偼僆乕儉懃偵廬傢側偄晹昳側偺偱丄廳偹崌傢偣偺尨棟傪偦偺傑傑巊偆帠偼偱偒傑偣傫丅偦偙偱丄揹埑亅揹棳摿惈恾偺嬋慄傪巊偭偰峫偊傑偡丅
壓恾塃懁偺摿惈恾偼丄忋偺摿惈恾偺侽丏俈倁晅嬤傪奼戝偟偨傕偺偱偡丅偙偺摿惈恾偵丄僟僀僆乕僪偵乮堦掕偺彫偝側岎棳揹埑倴倖傪壛偊側偑傜乯棳傟傞捈棳俬俥傪侽丏侾倣俙丄侾倣俙丄俁倣俙偲曄壔偝偣偨偲偒偺條巕傪帵偟傑偡丅
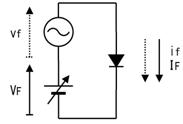 丂丂丂
丂丂丂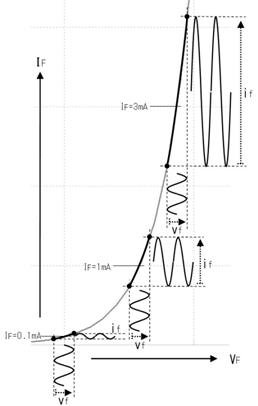
忋偺摿惈恾偐傜丄摨偠戝偒偝偺岎棳揹埑倴倖偑壛傢偭偰偄偰傕丄棳傟偰偄傞捈棳揹棳俬俥偑懡偄掱丄棳傟傞岎棳揹棳倝倖偑懡偔側傞偙偲偑暘傝傑偡丅偮傑傝僟僀僆乕僪偼丄捈棳揹棳偑憹偡偲岎棳偑棳傟堈偔側傞乮岎棳偺掞峈抣乮僀儞僺乕僟儞僗乯偑彫偝偔側傞乯偲暘傝傑偡丅
乮偙偺傛偆偵丄捈棳揹棳俬俥偑憹偊傞偲彫偝偔側傞乯僟僀僆乕僪偺僀儞僺乕僟儞僗倅俢偼師偺幃偱寁嶼偱偒傑偡丅
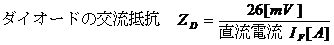
俤倶們倕倢偱偼丄=26E-3/I1
忋偺幃偵搊応偡傞俀俇倣倁偼丄僟僀僆乕僪偺嵽椏偑僔儕僐儞偱偁傞帠偐傜寛傑傞抣偱丄僔儕僐儞僟僀僆乕僪側傜偄偮傕摨偠偱偡丅椺偊偽丄侾倣俙偺捈棳偑棳傟偰偄傞帪偺僟僀僆乕僪偺僀儞僺乕僟儞僗偼丄
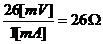
偲寁嶼偡傞偙偲偑偱偒傑偡丅
扐偟丄偙偺傛偆偵峫偊偰椙偄偺偼丄忋偺摿惈恾偐傜暘傞傛偆偵丄捈棳偵斾傋偰岎棳偑廫暘彫偝偄応崌乮彫怣崋夞楬偺応崌乯偩偗偱偡丅偮傑傝丄岎棳偺怳暆偑彫偝偗傟偽丄乽嬋慄乿偱弌棃偨摿惈恾偺堦晹暘傪乽捈慄乿偲峫偊偰丄偦偺偲偒偺岎棳掞峈乮僀儞僺乕僟儞僗乯傪寁嶼偡傞偙偲偑偱偒傑偡偑丄岎棳偺怳暆偑戝偒偔側傞偲丄乽嬋慄乿偺峀偄斖埻傪巊梡偟偰偟傑偆偨傔丄傕偼傗乽捈慄乿偲峫偊傞偙偲偑弌棃側偔側傝乮僆乕儉懃偑惉傝棫偮丄偮傑傝丄捈慄偱偁傞偙偲偑慜採偺乯僀儞僺乕僟儞僗偑寁嶼偱偒側偔側傝傑偡丅
侾侽.侾. 楙廗
忋恾偺夞楬偵棳傟傞捈棳揹棳偲岎棳揹棳傪丄壓恾傪嶲峫偵丄壓昞偵彂偒崬傫偱専摙偟偰偔偩偝偄丅
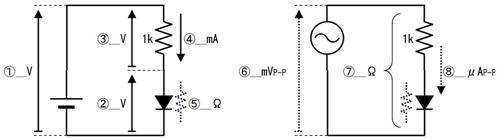
|
嘆
|
夞楬偵壛傢傞捈棳揹埑偼丄
|
倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僟僀僆乕僪偺弴揹埑倁俥偼丄
|
倁
|
|
嘊
|
侾倠兌偺椉抂揹埑偼丄
|
倁
|
|
嘋
|
侾倠兌偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘍
|
僟僀僆乕僪偺僀儞僺乕僟儞僗偼丄
俀俇倣倁亐侾倣俙亖俀俇兌
|
兌
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘐
|
夞楬偵壛傢傞岎棳揹埑偼丄
|
倣倁
|
|
嘑
|
僟僀僆乕僪偺僀儞僺乕僟儞僗偲掞峈傪崌寁偟偰丄
|
兌
|
|
嘒
|
夞楬偵棳傟傞岎棳揹棳偼丄
|
兪俙
|
侾侽.俀. 摎
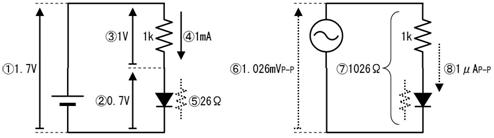
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
夞楬偵壛傢傞捈棳揹埑偼丄
|
侾丏俈倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僟僀僆乕僪偺弴揹埑倁俥偼丄
|
侽丏俈倁
|
|
嘊
|
侾倠兌偺椉抂揹埑偼丄
|
侾倁
|
|
嘋
|
侾倠兌偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘍
|
僟僀僆乕僪偺僀儞僺乕僟儞僗偼丄
俀俇倣倁亐侾倣俙亖俀俇兌
|
俀俇兌
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘐
|
夞楬偵壛傢傞岎棳揹埑偼丄
|
侾丏侽俀俇倣倁
|
|
嘑
|
僟僀僆乕僪偺僀儞僺乕僟儞僗偲掞峈傪崌寁偟偰丄
|
侾侽俀俇兌
|
|
嘒
|
夞楬偵棳傟傞岎棳揹棳偼丄
|
侾兪俙
|
偙偺傛偆偵丄僟僀僆乕僪偼僆乕儉懃偵廬傢側偄晹昳側偺偱丄偦偺傑傑偱偼乮廳偹崌傢偣偺尨棟傪巊偭偰乯捈棳偲岎棳傪暿乆偵峫偊傞偙偲偑偱偒傑偣傫丅偟偐偟丄乮岎棳偑捈棳偵斾傋偰廫暘彫偝偗傟偽丄偮傑傝丄彫怣崋夞楬偱偁傟偽乯捈棳偲岎棳傪暿乆偵峫傞偙偲偑偱偒傑偡丅偦偺偨傔丄愭偵捈棳偵偮偄偰峫偊丄棳傟傞捈棳偐傜僀儞僺乕僟儞僗傪媮傔偰丄師偵媮傔偨僀儞僺乕僟儞僗傪巊偭偰岎棳偵偮偄偰峫偊傞偙偲偑偱偒傑偡丅
侾侽.俁. 楙廗
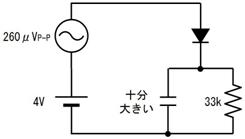
忋恾偺夞楬偵棳傟傞捈棳揹棳偲岎棳揹棳傪丄壓恾傪嶲峫偵丄壓昞偵彂偒崬傫偱専摙偟偰偔偩偝偄丅
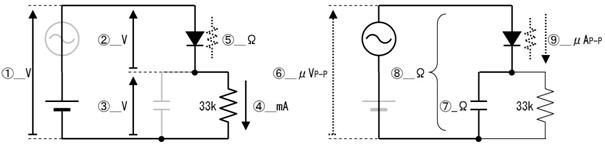
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
夞楬偵壛傢傞捈棳揹埑偼丄
|
係倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僟僀僆乕僪偺弴揹埑倁俥偼丄
|
侽丏俈倁
|
|
嘊
|
俁俁倠兌偺椉抂揹埑偼丄
|
俁丏俁倁
|
|
嘋
|
俁俁倠兌偵棳傟傞揹棳偼丄
|
侽丏侾倣俙
|
|
嘍
|
僟僀僆乕僪偺僀儞僺乕僟儞僗偼丄
俀俇倣倁亐侽丏侾倣俙亖俀俇侽兌
|
俀俇侽兌
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘐
|
夞楬偵壛傢傞岎棳揹埑偼丄
|
俀俇侽兪倁俹亅俹
|
|
嘑
|
廫暘戝偒側僐儞僨儞僒偺僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘒
|
僟僀僆乕僪偲僐儞僨儞僒偺捈楍僀儞僺乕僟儞僗偼丄
|
俀俇侽兌
|
|
嘓
|
夞楬偵棳傟傞岎棳揹棳偼丄
|
侾兪俙俹亅俹
|
侾侽.係. 摎
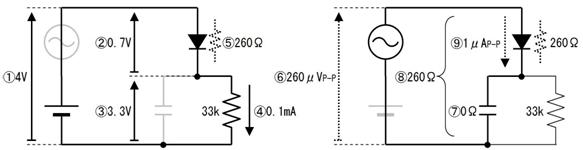
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
夞楬偵壛傢傞捈棳揹埑偼丄
|
係倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僟僀僆乕僪偺弴揹埑倁俥偼丄
|
侽丏俈倁
|
|
嘊
|
俁俁倠兌偺椉抂揹埑偼丄
|
俁丏俁倁
|
|
嘋
|
俁俁倠兌偵棳傟傞揹棳偼丄
|
侽丏侾倣俙
|
|
嘍
|
僟僀僆乕僪偺僀儞僺乕僟儞僗偼丄
俀俇倣倁亐侽丏侾倣俙亖俀俇侽兌
|
俀俇侽兌
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘐
|
夞楬偵壛傢傞岎棳揹埑偼丄
|
俀俇侽兪倁俹亅俹
|
|
嘑
|
廫暘戝偒側僐儞僨儞僒偺僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘒
|
僟僀僆乕僪偲僐儞僨儞僒偺捈楍僀儞僺乕僟儞僗偼丄
|
俀俇侽兌
|
|
嘓
|
夞楬偵棳傟傞岎棳揹棳偼丄
|
侾兪俙俹亅俹
|
僩儔儞僕僗僞夞楬偱偼丄柤慜傪暦偄偨偩偗偱丄捈棳偐丄彫怣崋偐偑暘偐傞傛偆偵丄揹埑傗揹棳偺屇傃柤偑岺晇偝傟偰偄傑偡丅
|
岎棳乛捈棳偺嬫暘
|
揹埑
|
揹棳
|
|
捈棳傗岎棳偵偙偩傢傜側偄
捈棳偲岎棳傪崌寁偟偨抣
|
揹埑偺婰崋乮戝暥帤乯倁偵丄戝暥帤偱抂巕偺柤慜傪揧偊傞丅
僄儈僢僞揹埑丗倁俠
儀乕僗揹埑丗倁俛
弌椡揹埑丗倁俷
屇傃曽丗僽僀丒僔乕摍
|
揹棳偺婰崋乮戝暥帤乯俬偵丄戝暥帤偱抂巕偺柤慜傪揧偊傞丅
僄儈僢僞揹埑丗俬俠
儀乕僗揹埑丗俬俛
弌椡揹埑丗俬俷
屇傃曽丗傾僀丒僔乕摍
|
|
捈棳
乮僶僀傾僗乯
|
揹埑偺婰崋乮戝暥帤乯倁偵丄戝暥帤偱抂巕偺柤慜傪俀偮揧偊傞丅
僄儈僢僞捈棳揹埑丗倁俠俠
儀乕僗捈棳揹埑丗倁俛俛
弌椡捈棳揹埑丗倁俷俷
屇傃曽丗僽僀丒僔乕丒僔乕摍
|
揹棳偺婰崋乮戝暥帤乯俬偵丄戝暥帤偱抂巕偺柤慜傪俀偮揧偊傞丅
僄儈僢僞捈棳揹埑丗俬俠俠
儀乕僗捈棳揹埑丗俬俛俛
弌椡捈棳揹埑丗俬俷俷
屇傃曽丗傾僀丒僔乕丒僔乕摍
|
|
岎棳
彫怣崋
乮怣崋乯
|
揹埑偺婰崋乮彫暥帤乯倴偵丄戝暥帤偱抂巕偺柤慜傪俀偮揧偊傞丅
僄儈僢僞岎棳揹埑丗倴們
儀乕僗岎棳揹埑丗倴倐
弌椡岎棳揹埑丗倴倧
屇傃曽丗僗儌乕儖丒僽僀丒僔乕摍
|
揹棳偺婰崋乮彫暥帤乯倝偵丄彫暥帤偱抂巕偺柤慜傪揧偊傞丅
僄儈僢僞岎棳揹埑丗倝們
儀乕僗岎棳揹埑丗倝倐
弌椡岎棳揹埑丗倝倧
屇傃曽丗僗儌乕儖丒傾僀丒僔乕摍
|
偦偺傑傑敪壒偟偨偺偱偼丄俬俠偲倝們偼偳偪傜傕乽傾僀丒僔乕乿偱嬫暿偱偒傑偣傫偐傜丄彫暥帤偺曽乮岎棳偺曽乯傪乽僗儌乕儖丒傾僀丒僔乕乿摍偲乽僗儌乕儖乿傪晅偗偰敪壒偡傞応崌傕偁傝傑偡丅傑偨丄捈棳揹棳乮揹埑乯傪僶僀傾僗揹棳乮揹埑乯偲丄岎棳揹棳乮揹埑乯傪怣崋揹棳乮揹埑乯偲屇傇応崌傕偁傝傑偡丅
僟僀僆乕僪偱偼丄棳傟傞捈棳偑暘傟偽丄僀儞僺乕僟儞僗傪抦傞偙偲偑偱偒傑偟偨丅僩儔儞僕僗僞偱傕儀乕僗偲僄儈僢僞偺娫偼僟僀僆乕僪偲峫偊傞偙偲偑偱偒傑偡丅偱偡偐傜丄僟僀僆乕僪偲摨條偵丄僄儈僢僞傪棳傟傞捈棳偑暘偐傟偽丄乮壓恾偵帵偡僟僀僆乕僪偲摨偠寁嶼偱乯僄儈僢僞偺僀儞僺乕僟儞僗傪抦傞偙偲偑偱偒傑偡丅偙偺僀儞僺乕僟儞僗傪丄乽僄儈僢僞摍壙僀儞僺乕僟儞僗乿乮倰倕乯偲屇傃傑偡丅
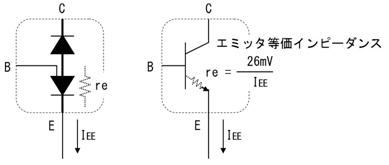
忋恾偵帵偡偲偍傝丄僄儈僢僞摍壙僀儞僺乕僟儞僗偼俀俇倣倁傪捈棳揹棳偱妱偭偰丄壓幃偱媮傔傞偙偲偑偱偒傑偡丅
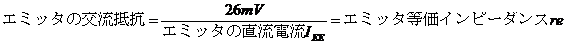
偨偲偊偽丄僄儈僢僞捈棳乮僶僀傾僗乯揹棳俬俤俤偑侾倣俙側傜丄倰倕偼俀俇兌偱偡丅偙偺倰倕偑暘偐傟偽丄僟僀僆乕僪偲摨條偵丄岎棳偺條巕傪専摙偡傞偙偲偑偱偒傑偡丅
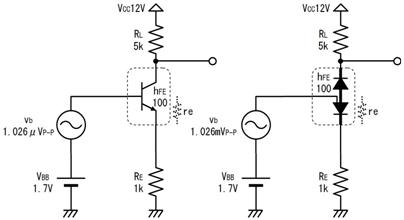
侾俀.侾. 楙廗
偱偼丄忋恾偺彫怣崋憹暆夞楬傪専摙偟傑偡丅忋恾偺夞楬傪丄壓恾傪嶲峫偵壓昞偵婰擖偟側偑傜丄捈棳偲岎棳偵偮偄偰専摙偟偰偔偩偝偄丅
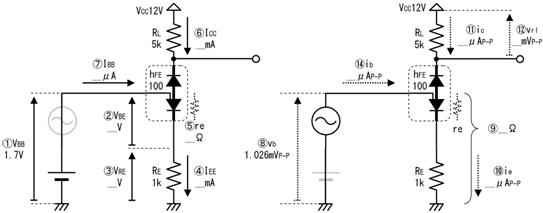
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
儀乕僗偵壛傢傞捈棳揹埑偼丄
|
侾丏俈倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘊
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘋
|
僄儈僢僞乮僶僀傾僗乯揹棳俬俤俤偼丄
|
倣俙
|
|
嘍
|
僄儈僢僞偲儀乕僗偺娫傪僟僀僆乕僪偲峫偊偨偲偒偺僀儞僺乕僟儞僗乮倰倕乯偼丄
|
兌
|
|
嘐
|
僐儗僋僞乮僶僀傾僗乯揹棳俬俠俠偼丄
|
倣俙
|
|
嘑
|
倛俥俤偑侾侽侽偩偐傜丄儀乕僗乮僶僀傾僗乯揹棳俬俛俛偼丄
|
兪俙
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘒
|
儀乕僗偵壛傢傞岎棳揹埑偼丄
|
侾丏侽俀俇倣倁俹亅俹
|
|
嘓
|
僄儈僢僞懁偺慡僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘔
|
僄儈僢僞偵棳傟傞揹棳偼丄
|
兪俙俹亅俹
|
|
嘕
|
僐儗僋僞偵棳傟傞揹棳偼丄乮俬俠亖俬俤偩偐傜丄乯
|
兪俙俹亅俹
|
|
嘖
|
晧壸掞峈俼俴偺椉抂偵敪惗偡傞揹埑偼丄
|
倣倁俹亅俹
|
|
嘗
|
岎棳偺怳暆偼栺壗攞偵戝偒偔側偭偰偄傑偡偐丄
|
栺丂丂攞
|
|
嘙
|
倛俥俤偑侾侽侽偩偐傜丄儀乕僗怣崋揹棳偼丄
|
兪俙
|
侾俀.俀. 摎
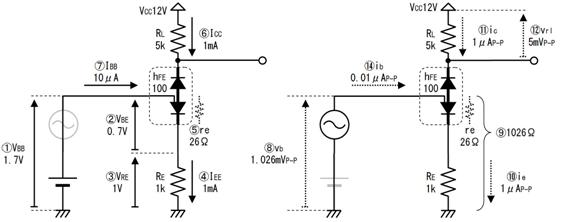
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
儀乕僗偵壛傢傞捈棳揹埑偼丄
|
侾丏俈倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘊
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
侾倁
|
|
嘋
|
僄儈僢僞乮僶僀傾僗乯揹棳俬俤俤偼丄
|
侾倣俙
|
|
嘍
|
僄儈僢僞偲儀乕僗偺娫傪僟僀僆乕僪偲峫偊偨偲偒偺僀儞僺乕僟儞僗乮倰倕乯偼丄
俀俇倣倁亐侾倣俙亖俀俇兌
|
俀俇兌
|
|
嘐
|
僐儗僋僞乮僶僀傾僗乯揹棳俬俠俠偼丄
|
侾倣俙
|
|
嘑
|
儀乕僗乮僶僀傾僗乯揹棳俬俛俛偼丄
|
侾侽兪俙
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘒
|
儀乕僗偵壛傢傞岎棳揹埑偼丄
|
侾丏侽俀俇倣倁俹亅俹
|
|
嘓
|
僄儈僢僞懁偺慡僀儞僺乕僟儞僗偼丄
|
侾侽俀俇兌
|
|
嘔
|
僄儈僢僞偵棳傟傞揹棳偼丄
|
侾兪俙俹亅俹
|
|
嘕
|
僐儗僋僞偵棳傟傞揹棳偼丄乮俬俠亖俬俤偩偐傜丄乯
|
侾兪俙俹亅俹
|
|
嘖
|
晧壸掞峈俼俴偺椉抂偵敪惗偡傞揹埑偼丄
|
俆倣倁俹亅俹
|
|
嘗
|
岎棳偺怳暆偼栺壗攞偵戝偒偔側偭偰偄傑偡偐丄
俆倣倁亐侾丏侽俀俇倣倁亖栺俆攞
|
栺俆攞
|
|
嘙
|
儀乕僗怣崋揹棳偼丄
倝們亐倛倖倕亖侾兪俙亐侾侽侽亖侽丏侽侾兪俙
|
侽丏侽侾兪俙
|
偙偺傛偆偵丄晧壸掞峈俼俴偺椉抂偵俆倣倁俹亅俹偺岎棳揹埑偑敪惗偟傑偟偨丅偙偺応崌偵丄弌椡抂巕偵尰傟傞揹埑傪峫偊傑偡丅
傑偢丄壓恾偺傛偆偵丄揹尮乮倁俠俠乯傕傾乕僗乮俧俶俢乯傕乮揹埑偑恔偊偰偄側偄偺偱乯岎棳揹埑偼偳偪傜傕侽倁偱丄岎棳偵偲偭偰偼摨偠揹埑偺応強偱偡丅乮壓恾偵 傗
傗 偱帵偟傑偡乯
偱帵偟傑偡乯
師偵丄崱夞偺夞楬偱偼丄晧壸掞峈俼俴偺椉抂偵丄壓恾嘇偺傛偆偵丄俆倣倁俹亅俹偺岎棳偑敪惗偟偰偄傑偟偨丅偙偙偱丄揹尮傕傾乕僗傕岎棳偵偲偭偰偼摨偠揹埑偺応強乮 乯偱偟偨偐傜丄壓恾嘊偺傛偆偵丄栴報傪弌椡抂巕偐傜傾乕僗偵岦偗偰昤偄偰傕乮岎棳偵偲偭偰偼乯摨偠偙偲偱偡丅
乯偱偟偨偐傜丄壓恾嘊偺傛偆偵丄栴報傪弌椡抂巕偐傜傾乕僗偵岦偗偰昤偄偰傕乮岎棳偵偲偭偰偼乯摨偠偙偲偱偡丅
壓恾嘊偺揹埑偼丄栴報偑壓傪岦偄偰偄傑偡丅偄偮傕偳偍傝偵栴報傪忋岦偒偵捈偡偲丄壓恾嘋偺傛偆偵丄揹埑偺嬌惈偼亅俆倣倁俹亅俹偲媡偵側傝傑偡丅
偮傑傝偙偺夞楬偼丄侾丏侽俀俇倣倁俹亅俹偺岎棳偑壛傢傞偲乮壓恾嘆乯丄亅俆倣倁俹亅俹乮壓恾嘋乯偑弌椡偝傟傑偡丅
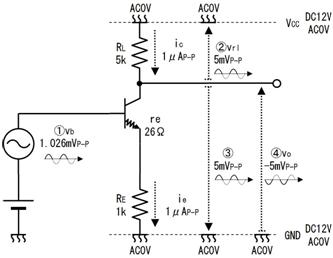
弌椡倴倧偺嬌惈偑儅僀僫僗偵側傞偺偼丄忋恾嘆偱擖椡偝傟偨攇偑丄忋壓媡偵側偭偰嘋偺傛偆偵弌椡偝傟傞偨傔偱偡丅
侾俀.俁. 楙廗
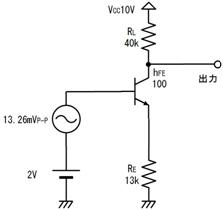
忋恾偺夞楬偱弌椡偝傟傞岎棳揹埑傪丄壓恾傪嶲峫偵丄壓昞偵婰擖偟側偑傜専摙偟偰偔偩偝偄丅
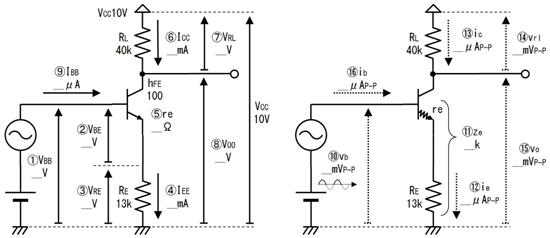
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
儀乕僗偵壛傢傞捈棳揹埑偼丄
|
倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘊
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘋
|
僄儈僢僞捈棳揹棳俬俤俤偼丄
|
倣俙
|
|
嘍
|
僄儈僢僞偲儀乕僗偺娫傪僟僀僆乕僪偲峫偊偨偲偒偺僀儞僺乕僟儞僗乮倰倕乯偼丄
|
兌
|
|
嘐
|
僐儗僋僞捈棳揹棳俬俠俠偼丄
|
倣俙
|
|
嘑
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
倁
|
|
嘒
|
弌椡捈棳揹棳倁俷俷偼丄
|
倁
|
|
嘓
|
儀乕僗捈棳揹棳俬俛俛偼丄
|
兪俙
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
|
|
嘔
|
儀乕僗偵壛傢傞岎棳揹埑偼丄
|
倣倁俹亅俹
|
|
嘕
|
僄儈僢僞懁偺慡僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘖
|
僄儈僢僞偵棳傟傞岎棳揹棳偼丄
|
兪俙俹亅俹
|
|
嘗
|
僐儗僋僞偵棳傟傞岎棳揹棳偼丄乮俬俠亖俬俤偩偐傜丄乯
|
兪俙俹亅俹
|
|
嘙
|
晧壸掞峈俼俴偺椉抂偵敪惗偡傞岎棳揹埑偼丄
|
倣倁俹亅俹
|
|
嘚
|
弌椡抂巕偵惗偠傞岎棳揹埑偼丄
|
倣倁俹亅俹
|
|
嘜
|
儀乕僗偵棳傟傞岎棳揹棳偼丄倛俥俤偑侾侽侽偩偐傜丄
|
兪俙
|
|
嘝
|
儀乕僗偵擖椡偟偨岎棳揹埑偼丄壗攞偵側偭偰弌椡偝傟偰偄傑偡偐丅
|
栺丂丂丂攞
|
侾俀.係. 摎
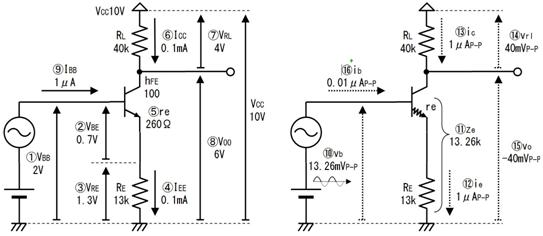
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
儀乕僗偵壛傢傞捈棳揹埑偼丄
|
俀倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘊
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
侾丏俁倁
|
|
嘋
|
僄儈僢僞捈棳揹棳俬俤俤偼丄
|
侽丏侾倣俙
|
|
嘍
|
僄儈僢僞偲儀乕僗偺娫傪僟僀僆乕僪偲峫偊偨偲偒偺僀儞僺乕僟儞僗乮倰倕乯偼丄
俀俇倣倁亐侽丏侾倣俙亖俀俇侽兌
|
俀俇侽兌
|
|
嘐
|
僐儗僋僞捈棳揹棳俬俠俠偼丄
|
侽丏侾倣俙
|
|
嘑
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
係倁
|
|
嘒
|
弌椡捈棳揹棳倁俷俷偼丄
|
俇倁
|
|
嘓
|
儀乕僗捈棳揹棳俬俛俛偼丄
|
侾兪俙
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
|
|
嘔
|
儀乕僗偵壛傢傞岎棳揹埑偼丄
|
侾俁丏俀俇倣倁俹亅俹
|
|
嘕
|
僄儈僢僞懁偺慡僀儞僺乕僟儞僗偼丄
|
侾俁丏俀俇倠兌
|
|
嘖
|
僄儈僢僞偵棳傟傞岎棳揹棳偼丄
|
侾兪俙俹亅俹
|
|
嘗
|
僐儗僋僞偵棳傟傞岎棳揹棳偼丄乮俬俠亖俬俤偩偐傜丄乯
|
侾兪俙俹亅俹
|
|
嘙
|
晧壸掞峈俼俴偺椉抂偵敪惗偡傞岎棳揹埑偼丄
|
係侽倣倁俹亅俹
|
|
嘚
|
弌椡抂巕偵惗偠傞岎棳揹埑偼丄
|
亅係侽倣倁俹亅俹
|
|
嘜
|
儀乕僗偵棳傟傞岎棳揹棳偼丄
倝們亐倛倖倕亖侾兪俙亐侾侽侽亖侽丏侽侾兪俙
|
侽丏侽侾兪俙
|
|
嘝
|
儀乕僗偵擖椡偟偨岎棳揹埑偼丄壗攞偵側偭偰弌椡偝傟偰偄傑偡偐丅
係侽倣倁亐侾俁丏俀俇倣倁亖栺俁攞
|
栺俁攞
|
偙偺僞僀僾偺夞楬偺憹暆棪偼俼俴亐乮倰倕亄俼俤乯偱媮傔傞偙偲偑偱偒傑偡丅偙偺傛偆偵丄僄儈僢僞掞峈偑偁傞憹暆婍偼乮埨掕偟偰偄傑偡偑乯憹暆棪偑彫偝偔側傝傑偡丅
壓恾偺傛偆偵丄僄儈僢僞掞峈偲暲楍偵僐儞僨儞僒傪庢傝晅偗傟偽丄夞楬偺埨掕惈傪曐偭偨傑傑丄憹暆棪傪戝偒偔偱偒傑偡丅偙偺僐儞僨儞僒傪乽僄儈僢僞僶僀僷僗僐儞僨儞僒乿偲屇傃傑偡丅
捈棳偐傜尒傟偽僄儈僢僞掞峈偑偁傝丄偦偺偨傔偵夞楬偼乮壏搙偑曄壔偡傞摍偟偰傕乯埨掕偟偰偄傑偡偟丄岎棳偐傜尒傟偽僄儈僢僞掞峈偑側偄偨傔丄僄儈僢僞偵戲嶳偺岎棳揹棳偑棳傟偰丄憹暆棪傪戝偒偔偱偒傑偡丅
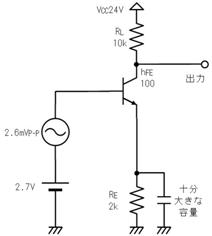
侾俁.侾. 楙廗
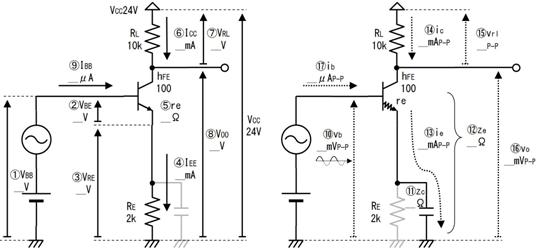
忋恾偺夞楬傪壓昞偵彂偒崬傒側偑傜捈棳偲岎棳偵偮偄偰専摙偟丄岎棳弌椡揹埑傪媮傔偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
儀乕僗偵壛傢傞捈棳揹埑偼丄
|
倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘊
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘋
|
僄儈僢僞捈棳揹棳俬俤俤偼丄
|
倣俙
|
|
嘍
|
僄儈僢僞偲儀乕僗偺娫傪僟僀僆乕僪偲峫偊偨偲偒偺僀儞僺乕僟儞僗乮倰倕乯偼丄
|
兌
|
|
嘐
|
僐儗僋僞捈棳揹棳俬俠俠偼丄
|
倣俙
|
|
嘑
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
倁
|
|
嘒
|
弌椡捈棳揹棳倁俷俷偼丄
|
倁
|
|
嘓
|
儀乕僗捈棳揹棳俬俛俛偼丄
|
兪俙
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
|
|
嘔
|
儀乕僗偵壛傢傞岎棳揹埑偼丄
|
倣倁俹亅俹
|
|
嘕
|
廫暘戝偒側梕検偺僐儞僨儞僒偺僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘖
|
僄儈僢僞懁偺慡僀儞僺乕僟儞僗偼丄
倰倕亄倸們亖俀俇兌亄侽兌亖俀俇兌
|
兌
|
|
嘗
|
僄儈僢僞偵棳傟傞岎棳揹棳倝倕偼丄
|
倣俙俹亅俹
|
|
嘙
|
僐儗僋僞偵棳傟傞岎棳揹棳偼丄乮俬俠亖俬俤偩偐傜丄乯
|
倣俙俹亅俹
|
|
嘚
|
晧壸掞峈俼俴偺椉抂偵敪惗偡傞岎棳揹埑偼丄
|
倁俹亅俹
|
|
嘜
|
弌椡抂巕偵惗偠傞岎棳揹埑偼丄
|
倁俹亅俹
|
|
嘝
|
儀乕僗偵棳傟傞岎棳揹棳偼丄
|
兪俙
|
|
嘠
|
儀乕僗偵擖椡偟偨岎棳揹埑偼丄壗攞偵側偭偰弌椡偝傟偰偄傑偡偐丅
|
攞
|
侾俁.俀. 摎
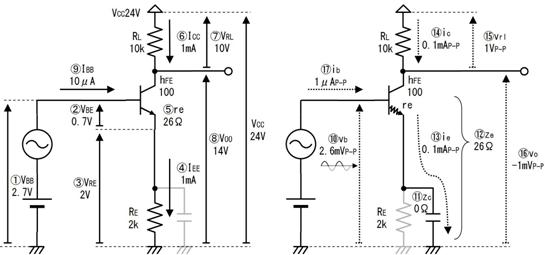
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
儀乕僗偵壛傢傞捈棳揹埑偼丄
|
俀丏俈倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘊
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
俀倁
|
|
嘋
|
僄儈僢僞捈棳揹棳俬俤俤偼丄
|
侾倣俙
|
|
嘍
|
僄儈僢僞偲儀乕僗偺娫傪僟僀僆乕僪偲峫偊偨偲偒偺僀儞僺乕僟儞僗乮倰倕乯偼丄
俀俇倣倁亐侾倣俙亖俀俇兌
|
俀俇兌
|
|
嘐
|
僐儗僋僞捈棳揹棳俬俠俠偼丄
|
侾倣俙
|
|
嘑
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
侾侽倁
|
|
嘒
|
弌椡捈棳揹棳倁俷俷偼丄
|
侾係倁
|
|
嘓
|
儀乕僗捈棳揹棳俬俛俛偼丄
|
侾侽兪俙
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
|
|
嘔
|
儀乕僗偵壛傢傞岎棳揹埑偼丄
|
俀丏俇倣倁俹亅俹
|
|
嘕
|
廫暘戝偒側梕検偺僐儞僨儞僒偺僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘖
|
僄儈僢僞懁偺慡僀儞僺乕僟儞僗偼丄
倰倕亄倸們亖俀俇兌亄侽兌亖俀俇兌
|
俀俇兌
|
|
嘗
|
僄儈僢僞偵棳傟傞岎棳揹棳倝倕偼丄
|
侽丏侾倣俙俹亅俹
|
|
嘙
|
僐儗僋僞偵棳傟傞岎棳揹棳偼丄乮俬俠亖俬俤偩偐傜丄乯
|
侽丏侾倣俙俹亅俹
|
|
嘚
|
晧壸掞峈俼俴偺椉抂偵敪惗偡傞岎棳揹埑偼丄
|
侾倁俹亅俹
|
|
嘜
|
弌椡抂巕偵惗偠傞岎棳揹埑偼丄
|
亅侾倁俹亅俹
|
|
嘝
|
儀乕僗偵棳傟傞岎棳揹棳偼丄
倝們亐倛倖倕亖侽丏侾倣俙亐侾侽侽亖侾兪俙
|
侾兪俙
|
|
嘠
|
儀乕僗偵擖椡偟偨岎棳揹埑偼丄壗攞偵側偭偰弌椡偝傟偰偄傑偡偐丅
侾倁亐俀丏俇倣倁亖俁俉侽攞
|
俁俉侽攞
|
偙偺傛偆偵丄僄儈僢僞僶僀僷僗僐儞僨儞僒傪庢傝晅偗傞偲丄憹暆棪偑戝偒偔側傝傑偡丅偙偺僞僀僾偺夞楬偺憹暆棪偼丄俼俴亐倰倕偱媮傔傞偙偲偑偱偒傑偡丅
偟偐偟丄乮岎棳偐傜尒傞偲丄僄儈僢僞掞峈偑柍偔側傝乯儀乕僗偲僄儈僢僞偺娫乮俛亅俤娫乯偵戝偒側岎棳揹埑偑壛傢傞偨傔丄攇宍偑榗傒傑偡丅壓恾偵偦偺條巕傪帵偟傑偡丅偙偺恾偱偼丄僌儔僼壓懁偐傜擖偭偰偒偨岎棳偑憹暆偝傟偰丄僌儔僼塃懁偵弌椡偝傟傑偡偑丄弌椡攇宍偼嵟弶偺攇宍偲戝偒偔堎側偭偰偄傑偡丅
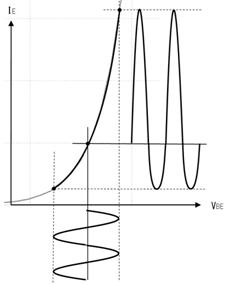
忋恾偱暘偐傞傛偆偵丄倁俛俤偲俬俤偺摿惈偼嬋慄偱偡丅嬋慄偵増偭偰夞楬偑摦嶌偡傞偲丄偐側傜偢攇宍偑榗傒傑偡丅偦偙偱彫怣崋夞楬偱偼乽捈棳揹埑乮揹棳乯偵斾傋偰丄岎棳揹埑乮揹棳乯偑廫暘偵彫偝偄乿偲偄偆儖乕儖傪愝偗偰乮杮摉偼嬋慄偱偁傞摿惈偺乽嬌堦晹乿偩偗傪巊梡偟偰乯捈慄偵増偭偰夞楬傪摦嶌偝偣丄怣崋傪榗傑偝偢偵憹暆偟偰偄傑偟偨丅
偟偐偟丄忋恾偺傛偆偵怣崋偑乮捈棳偵斾傋偰乯戝偒偔側傞偲丄偲偰傕乽嬌堦晹乿偲偼尵偊側偔側偭偰偟傑偄丄嬋慄偵増偭偰夞楬偑摦嶌偟丄攇宍偑榗傒傑偡丅
捈棳揹棳偲岎棳揹棳偺戝偒偝傪丄忋偱楙廗偟偨夞楬偱斾妑偡傞偲丄嘋僄儈僢僞捈棳揹棳偑侾倣俙偱丄嘗僄儈僢僞岎棳揹棳偑侽丏侾倣俙偲丄捈棳偵偔傜傋偰岎棳偑侾侽暘偺侾彫偝偄偩偗偱偡丅榗傒偺彮側偄憹暆傪峴偆偨傔偵偼丄岎棳揹棳傪捈棳揹棳偺侾侽侽暘偺侾掱搙埲壓偵彫偝偔偡傞偙偲偑昁梫偱偡丅
傕偪傠傫丄摨偠夞楬偱傕怣崋偺怳暆偑彫偝偐偭偨傝丄榗偑婥偵側傜側偄応崌偼丄忋偺楙廗偺夞楬偱戝偒側憹暆棪傪摼傞偙偲傕壜擻偱偡丅扐偟丄偁傑傝偵憹暆棪偑戝偒偔丄摦嶌偑晄埨掕偵側傞乮敪怳偡傞乯応崌傕偁傝傑偡丅
侾俁.俁. 楙廗
壓恾偺夞楬傕僄儈僢僞僶僀僷僗僐儞僨儞僒傪愝偗偨憹暆夞楬偱偡丅偙偺夞楬偱偼丄俼俤侾傪捛壛偟偰僄儈僢僞懁偺僀儞僺乕僟儞僗傪戝偒偔偟丄怣崋揹棳傪彫偝偔偟偰偄傑偡丅偙傟偵傛偭偰憹暆棪偼彫偝偔側傝傑偡偑丄攇宍偺榗偑彫偝偔側傝傑偡丅
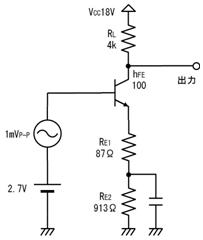
忋恾偺夞楬偱弌椡偝傟傞岎棳揹埑傪丄壓恾傪嶲峫偵丄壓昞偵婰擖偟側偑傜専摙偟偰偔偩偝偄丅
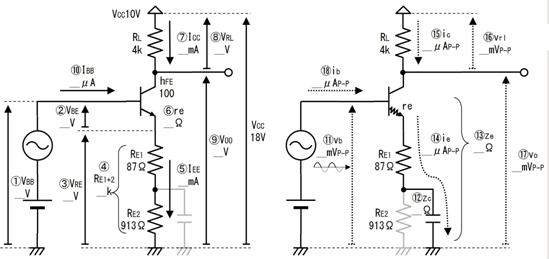
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
儀乕僗偵壛傢傞捈棳揹埑偼丄
|
倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘊
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘋
|
僄儈僢僞掞峈俼俤侾偲俼俤俀偺捈楍崌惉掞峈偼丄
|
倠兌
|
|
嘍
|
僄儈僢僞捈棳揹棳俬俤俤偼丄
|
倣俙
|
|
嘐
|
僄儈僢僞偲儀乕僗偺娫傪僟僀僆乕僪偲峫偊偨偲偒偺僀儞僺乕僟儞僗乮倰倕乯偼丄
|
兌
|
|
嘑
|
僐儗僋僞捈棳揹棳俬俠俠偼丄
|
倣俙
|
|
嘒
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
倁
|
|
嘓
|
弌椡捈棳揹棳倁俷俷偼丄
|
倁
|
|
嘔
|
儀乕僗捈棳揹棳俬俛俛偼丄
|
兪俙
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
|
|
嘕
|
儀乕僗偵壛傢傞岎棳揹埑偼丄
|
倣倁俹亅俹
|
|
嘖
|
廫暘戝偒側梕検偺僐儞僨儞僒偺僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘗
|
僄儈僢僞懁偺慡僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘙
|
僄儈僢僞偵棳傟傞岎棳揹棳偼丄
|
兪俙俹亅俹
|
|
嘚
|
僐儗僋僞偵棳傟傞岎棳揹棳偼丄乮俬俠亖俬俤偩偐傜丄乯
|
兪俙俹亅俹
|
|
嘜
|
晧壸掞峈俼俴偺椉抂偵敪惗偡傞岎棳揹埑偼丄
|
倣倁俹亅俹
|
|
嘝
|
弌椡抂巕偵惗偠傞岎棳揹埑偼丄
|
倣倁俹亅俹
|
|
嘠
|
儀乕僗偵棳傟傞岎棳揹棳偼丄
|
兪俙
|
|
嘡
|
儀乕僗偵擖椡偟偨岎棳揹埑偼丄壗攞偵側偭偰弌椡偝傟偰偄傑偡偐丅
|
攞
|
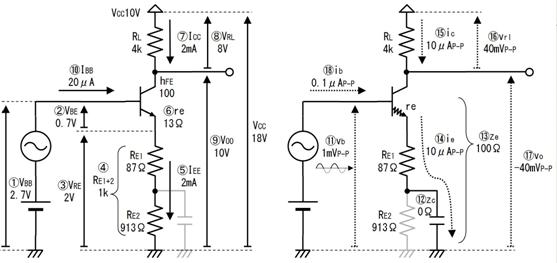
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
儀乕僗偵壛傢傞捈棳揹埑偼丄
|
俀丏俈倁
|
|
嘇
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘊
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
俀倁
|
|
嘋
|
僄儈僢僞掞峈俼俤侾偲俼俤俀偺捈楍崌惉掞峈偼丄
|
侾倠兌
|
|
嘍
|
僄儈僢僞捈棳揹棳俬俤俤偼丄
|
俀倣俙
|
|
嘐
|
僄儈僢僞偲儀乕僗偺娫傪僟僀僆乕僪偲峫偊偨偲偒偺僀儞僺乕僟儞僗乮倰倕乯偼丄
俀俇倣倁亐俀倣俙亖侾俁兌
|
侾俁兌
|
|
嘑
|
僐儗僋僞捈棳揹棳俬俠俠偼丄
|
俀倣俙
|
|
嘒
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
俉倁
|
|
嘓
|
弌椡捈棳揹棳倁俷俷偼丄
|
侾侽倁
|
|
嘔
|
儀乕僗捈棳揹棳俬俛俛偼丄
|
俀侽兪俙
|
|
|
岎棳偵偮偄偰峫偊傑偡丅
|
|
|
嘕
|
儀乕僗偵壛傢傞岎棳揹埑偼丄
|
侾倣倁俹亅俹
|
|
嘖
|
廫暘戝偒側梕検偺僐儞僨儞僒偺僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘗
|
僄儈僢僞懁偺慡僀儞僺乕僟儞僗偼丄
|
侾侽侽兌
|
|
嘙
|
僄儈僢僞偵棳傟傞岎棳揹棳偼丄
|
侾侽兪俙俹亅俹
|
|
嘚
|
僐儗僋僞偵棳傟傞岎棳揹棳偼丄乮俬俠亖俬俤偩偐傜丄乯
|
侾侽兪俙俹亅俹
|
|
嘜
|
晧壸掞峈俼俴偺椉抂偵敪惗偡傞岎棳揹埑偼丄
|
係侽倣倁俹亅俹
|
|
嘝
|
弌椡抂巕偵惗偠傞岎棳揹埑偼丄
|
亅係侽倣倁俹亅俹
|
|
嘠
|
儀乕僗偵棳傟傞岎棳揹棳偼丄
倝們亐倛倖倕亖侾侽兪俙亐侾侽侽亖侽丏侾兪俙
|
侽丏侾兪俙
|
|
嘡
|
儀乕僗偵擖椡偟偨岎棳揹埑偼丄壗攞偵側偭偰弌椡偝傟偰偄傑偡偐丅
係侽倣倁亐侾倣倁亖係侽攞
|
係侽攞
|
偙偺傛偆偵丄俼俤侾傪捛壛偡傞偙偲偱丄憹暆棪偼係侽攞偲彫偝偔側傝傑偡丅偙偺僞僀僾偺夞楬偺憹暆棪偼丄俼俴亐乮倰倕亄俼俤侾乯偱媮傔傞偙偲偑偱偒傑偡丅傑偨丄嘔儀乕僗捈棳揹棳俀侽兪俙偵懳偟偰丄嘠儀乕僗岎棳揹棳偼侽丏侾兪俙偲丄俀侽侽暘偺侾偵彫偝偔側偭偰偍傝丄榗傒偼彮側偔側傝傑偡丅
偝偰丄偙傟傑偱楙廗偟偨夞楬偱偼丄壓恾嵍懁偺傛偆偵丄怣崋偵捈棳傪愙懕偟偰夞楬偵壛偊偰偄傑偟偨丅偟偐偟捠忢偺怣崋偵偼捈棳偑娷傑傟偰偄傑偣傫丅偦偙偱婛偵愢柧偟偨乽暘埑僶僀傾僗乿偺曽朄傪棙梡偟偰丄壓恾塃偺傛偆側夞楬偱丄儀乕僗偵堦掕偺揹埑乮偙偙偱偼丄侾丏俈倁乯傪壛偊傑偡丅
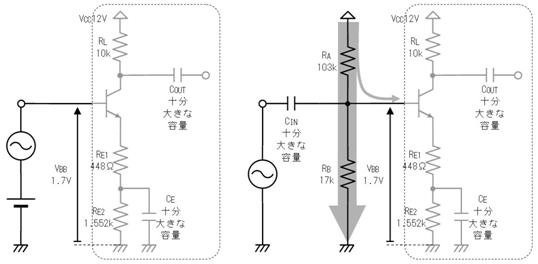
忋恾塃偺夞楬偱偼乮儀乕僗揹棳偑倛俥俤偺僶儔僣僉偱曄壔偡傞偺偱乯忋恾塃偺俼俙偲俼俛偵偼儀乕僗揹棳偺侾侽攞乣侾侽侽攞偺揹棳傪棳偡偺偑億僀儞僩偱偟偨丅
侾係.侾. 楙廗
忋恾偺夞楬傪丄壓恾傪嶲峫偵壓昞偵彂偒崬傒側偑傜専摙偟丄怣崋乮岎棳乯憹暆棪傪媮傔偰壓偝偄丅
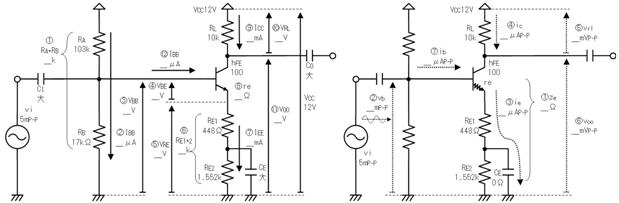
|
斣崋
|
幙栤
|
抣
|
|
|
忋恾嵍懁傪巊偭偰丄捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
暘埑僶僀傾僗掞峈俼俙偲俼俛偺崌寁偼丄
|
倠兌
|
|
嘇
|
俼俙偲俼俛偵棳傟傞揹棳偼丄
|
兪俙
|
|
嘊
|
儀乕僗僶僀傾僗揹埑倁俛俛偼丄
|
倁
|
|
嘋
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
|
倁
|
|
嘍
|
俼俤侾偲俼俤俀偺捈楍晹暘偵壛傢傞揹埑偼丄
|
倁
|
|
嘐
|
俼俤侾偲俼俤俀偺捈楍崌惉掞峈偼丄
|
倠兌
|
|
嘑
|
僄儈僢僞僶僀傾僗揹棳俬俤俤偼丄
|
倣俙
|
|
嘒
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕偼丄
|
兌
|
|
嘓
|
僐儗僋僞僶僀傾僗揹棳俬俠俠偼丄
|
倣俙
|
|
嘔
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
倁
|
|
嘕
|
弌椡捈棳揹埑倁俷俷偼丄
|
倁
|
|
嘖
|
儀乕僗僶僀傾僗揹棳俬俛俛偼丄
|
兪俙
|
|
|
忋恾塃懁傪巊偭偰丄岎棳偵偮偄偰峫偊傑偡丅
|
|
|
嘆
|
僄儈僢僞懁偺崌寁僀儞僺乕僟儞僗倅倕偼丄
|
兌
|
|
嘇
|
儀乕僗偵壛傢傞岎棳乮怣崋乯揹埑偼丄
|
倣倁俹亅俹
|
|
嘊
|
僄儈僢僞岎棳揹埑倝倕偼丄
|
兪俙俹亅俹
|
|
嘋
|
僐儗僋僞岎棳揹埑倝們偼丄
|
兪俙俹亅俹
|
|
嘍
|
晧壸掞峈俼俴偺椉抂偺岎棳揹埑倴倰倢偼丄
|
倣倁俹亅俹
|
|
嘐
|
弌椡抂巕偺岎棳揹埑倴倧倧偼丄
|
倣倁俹亅俹
|
|
嘑
|
儀乕僗岎棳揹棳倝倐倐偼丄
|
兪俙俹亅俹
|
|
嘒
|
僄儈僢僞僶僀傾僗揹棳偼丄僄儈僢僞岎棳揹棳偺壗攞丄
|
攞
|
侾係.俀. 摎
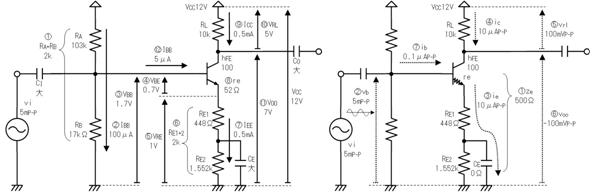
|
斣崋
|
幙栤
|
抣
|
|
|
忋恾嵍懁傪巊偭偰丄捈棳偵偮偄偰峫偊傑偡丅
|
亅
|
|
嘆
|
暘埑僶僀傾僗掞峈俼俙偲俼俛偺崌寁偼丄
|
侾俀侽倠兌
|
|
嘇
|
俼俙偲俼俛偵棳傟傞揹棳偼丄
|
侾侽侽兪俙
|
|
嘊
|
儀乕僗僶僀傾僗揹埑倁俛俛偼丄
|
侾丏俈倁
|
|
嘋
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
|
侽丏俈倁
|
|
嘍
|
俼俤侾偲俼俤俀偺捈楍晹暘偵壛傢傞揹埑偼丄
|
侾倁
|
|
嘐
|
俼俤侾偲俼俤俀偺捈楍崌惉掞峈偼丄
|
俀倠兌
|
|
嘑
|
僄儈僢僞僶僀傾僗揹棳俬俤俤偼丄
|
侽丏俆倣俙
|
|
嘒
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕偼丄
|
俆俀兌
|
|
嘓
|
僐儗僋僞僶僀傾僗揹棳俬俠俠偼丄
|
侽丏俆倣俙
|
|
嘔
|
晧壸掞峈俼俴偺椉抂揹埑偼丄
|
俆倁
|
|
嘕
|
弌椡捈棳揹埑倁俷俷偼丄
|
俈倁
|
|
嘖
|
儀乕僗僶僀傾僗揹棳俬俛俛偼丄
|
俆兪俙
|
|
|
忋恾塃懁傪巊偭偰丄岎棳偵偮偄偰峫偊傑偡丅
|
|
|
嘆
|
僄儈僢僞懁偺崌寁僀儞僺乕僟儞僗倅倕偼丄
|
俆侽侽兌
|
|
嘇
|
儀乕僗偵壛傢傞岎棳乮怣崋乯揹埑偼丄
|
俆倣倁俹亅俹
|
|
嘊
|
僄儈僢僞岎棳揹埑倝倕偼丄
|
侾侽兪俙俹亅俹
|
|
嘋
|
僐儗僋僞岎棳揹埑倝們偼丄
|
侾侽兪俙俹亅俹
|
|
嘍
|
晧壸掞峈俼俴偺椉抂偺岎棳揹埑倴倰倢偼丄
|
侾侽侽倣倁俹亅俹
|
|
嘐
|
弌椡抂巕偺岎棳揹埑倴倧倧偼丄
|
亅侾侽侽倣倁俹亅俹
|
|
嘑
|
儀乕僗岎棳揹棳倝倐倐偼丄
|
侽丏侾兪俙俹亅俹
|
|
嘒
|
僄儈僢僞僶僀傾僗揹棳偼丄僄儈僢僞岎棳揹棳偺壗攞丄
|
俆侽攞
|
偝偰丄楙廗偱傕庢傝埖偭偨壓恾嵍偺憹暆夞楬偺弌椡揹埑偼丄侾侽侽倣倁俹亅俹偱偟偨丅侾侽侽倣倁偁傟偽僗僺乕僇乕傕懡彮偼柭傞偼偢偱偡丅偦偙偱丄壓恾拞墰偺傛偆偵俉兌偺僗僺乕僇乕傪愙懕偡傞偲丄壒偑弌傑偣傫丅偙偺偲偒弌椡抂巕偺怣崋揹埑傪應掕偡傞偲丄侽丏侽俉倣倁俹亅俹偟偐弌椡偝傟偰偄傑偣傫丅
偙偺傛偆偵憹暆婍偵晧壸傪愙懕偡傞偲弌椡揹埑偑掅壓偟傑偡丅偙傟偼丄壓恾塃懁偵帵偡傛偆偵丄憹暆婍偺撪晹偵乽弌椡僀儞僺乕僟儞僗乿偲屇傇掞峈偑偁傞偨傔偱偡丅
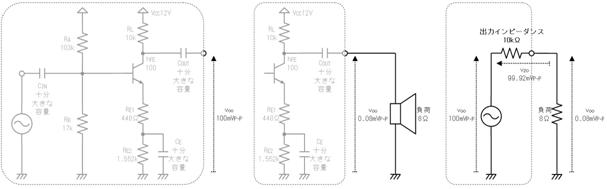
憹暆婍偺弌椡傪棙梡偡傞偲偒丄乽偳偺掱搙偺乮僀儞僺乕僟儞僗偺乯晧壸傪宷偄偩傜椙偄偐乿偁傞偄偼乽晧壸傪愙懕偡傞偲丄弌椡揹埑偼偄偔傜偵側傞偐乿傪抦傞偨傔偵偼丄弌椡僀儞僺乕僟儞僗偺抣偑廳梫偱偡丅
憹暆婍偼弌椡僀儞僺乕僟儞僗偲摨偠抣偺晧壸掞峈傪愙懕偟偨偲偒嵟傕戝偒側揹椡傪庢傝弌偡偙偲偑偱偒傑偡丅
傑偨丄壓恾乮倎乯偺傛偆偵丄柍晧壸偱弌椡揹埑侾侽侽倣倁俹亅俹偺夞楬偵丄壓恾乮倐乯偺傛偆偵丄師抜偺憹暆夞楬傪愙懕偡傞偲丄侾侽侽倣倁偱偁偭偨弌椡揹埑偑丄俆俁倣倁俹亅俹偵掅壓偟傑偟偨丅偙傟偼丄壓恾乮們乯偵帵偡傛偆偵丄師抜偺憹暆婍偺擖椡晹偵乽擖椡僀儞僺乕僟儞僗乿偲屇傇掞峈偑偁傝丄偙傟偑愙懕偝傟偨偙偲偱丄慜抜偺憹暆婍偺弌椡揹埑偑掅壓偡傞偨傔偱偡丅
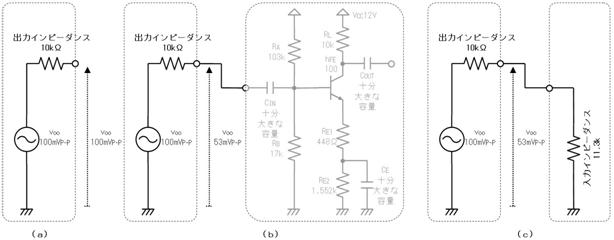
偙偺傛偆偵丄憹暆婍傪怣崋偵愙懕偡傞偲偒乽愙懕偡傞偲丄怣崋偺揹埑偼偄偔傜偵側傞偐乿傪抦傞偨傔偵偼丄擖椡僀儞僺乕僟儞僗偺抣偑廳梫偱偡丅
偙偺傛偆側棟桼偱丄憹暆婍偺弌椡僀儞僺乕僟儞僗偲擖椡僀儞僺乕僟儞僗偼丄懠偺夞楬偲愙懕偟偨偲偒偺條巕傪抦傞偨傔偵廳梫偱偡丅擖椡僀儞僺乕僟儞僗偼倅倝傗倅倝値丄弌椡僀儞僺乕僟儞僗偼倅倧傗倅倧倳倲偺婰崋偱昞偟傑偡丅
偱偼丄擖椡僀儞僺乕僟儞僗傗弌椡僀儞僺乕僟儞僗乮擖弌椡僀儞僺乕僟儞僗乯傪媮傔傞曽朄傪愢柧偟傑偡丅
椺偊偽丄壓恾乮倎乯偺夞楬偺擖椡僀儞僺乕僟儞僗偼丄壓恾乮倐乯偺傛偆側庤弴偱媮傔傑偡丅偙偺曽朄偱偼丄乽傾乕僗傕揹尮傕乮揹埑偺怳摦偑柍偄揰偩偐傜乯岎棳偵偲偭偰偼傾乕僗偱偁傞乿偲峫偊傑偡丅
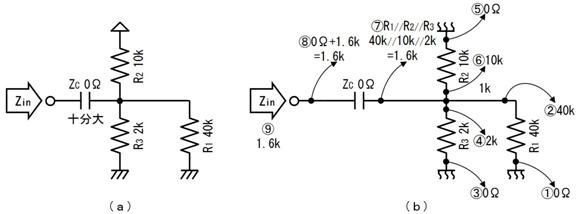
侾俆.侾. 妋擣
忋恾乮倐乯傪尒側偑傜丄壓昞偵婰擖偟偰丄忋恾偺夞楬偺擖椡僀儞僺乕僟儞僗傪媮傔偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俼侾偺壓懁偐傜傾乕僗傪尒傟偽丄
|
兌
|
|
嘇
|
俼侾偺忋懁偐傜傾乕僗傪尒傟偽丄
|
倠兌
|
|
嘊
|
俼俁偺壓懁偐傜傾乕僗傪尒傟偽丄
|
兌
|
|
嘋
|
俼俁偺忋懁偐傜傾乕僗傪尒傟偽丄
|
倠兌
|
|
嘍
|
乮揹尮偼岎棳偵偲偭偰偼傾乕僗偲摨偠侽倁偩偐傜丄乯
俼俀偺忋懁偐傜揹尮傪尒傟偽丄
|
兌
|
|
嘐
|
俼俀偺壓懁偐傜揹尮傪尒傟偽丄
|
倠兌
|
|
嘑
|
僐儞僨儞僒偺塃懁偐傜丄塃懁傪尒傟偽丄
偙傟傑偱偵媮傔偨俁偮偺僀儞僺乕僟儞僗偑暲楍偵尒偊偰丄係侽倠乛乛侾侽倠乛乛俀倠
|
倠
|
|
嘒
|
擖椡抂巕乮僐儞僨儞僒偺嵍懁乯偐傜丄夞楬慡懱傪尒傟偽丄
忋偱媮傔偨僀儞僺乕僟儞僗偲僐儞僨儞僒偺僀儞僺乕僟儞僗偑捈楍偵尒偊偰丄
侽兌亄侾丏俇倠兌
|
倠兌
|
侾俆.俀. 摎
偙偺傛偆偵偟偰丄忋恾偺夞楬偺擖椡僀儞僺乕僟儞僗傪侾丏俇倠兌偲抦傞偙偲偑偱偒傑偡丅
侾俆.俁. 楙廗
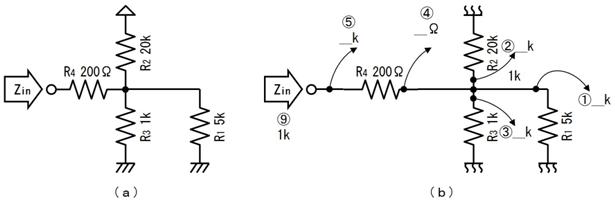
忋恾乮倎乯偺夞楬偺擖椡僀儞僺乕僟儞僗傪丄忋恾乮倐乯偺峫偊曽偱丄壓昞偵彂偒崬傒側偑傜媮傔偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俼侾偺忋懁偐傜傾乕僗傪尒傟偽丄
|
倠兌
|
|
嘇
|
俼俀偺壓懁偐傜揹尮傪尒傟偽丄
|
倠兌
|
|
嘊
|
俼俁偺忋懁偐傜傾乕僗傪尒傟偽丄
|
倠兌
|
|
嘋
|
俼係偺塃懁偐傜丄塃懁傪尒傟偽丄
嘆乣嘊偺僀儞僺乕僟儞僗偑暲楍偵尒偊偰丄
|
兌
|
|
嘍
|
擖椡抂巕偐傜夞楬慡懱傪尒傟偽丄
忋偺嘋偺僀儞僺乕僟儞僗偵丄俼係偺僀儞僺乕僟儞僗偑壛傢偭偰丄
|
倠兌
|
侾俆.係. 摎
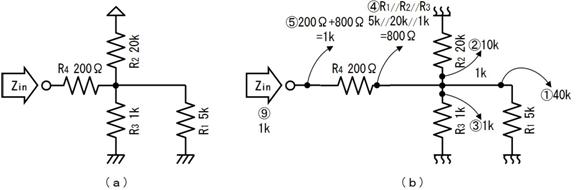
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俼侾偺忋懁偐傜傾乕僗傪尒傟偽丄
|
俆倠兌
|
|
嘇
|
俼俀偺壓懁偐傜揹尮傪尒傟偽丄
|
俀侽倠兌
|
|
嘊
|
俼俁偺忋懁偐傜傾乕僗傪尒傟偽丄
|
侾倠兌
|
|
嘋
|
俼係偺塃懁偐傜丄塃懁傪尒傟偽丄
俆倠乛乛俀侽倠乛乛侾倠亖俉侽侽兌
|
俉侽侽兌
|
|
嘍
|
擖椡抂巕偐傜夞楬慡懱傪尒傟偽丄
俀侽侽兌亄俉侽侽兌亖侾倠兌
|
侾倠兌
|
壓恾偺傛偆偵丄儀乕僗揹棳偺倛俥俤攞偑僐儗僋僞偵棳傟傞偨傔丄椺偊偽丄儀乕僗揹棳偑侾侽兪俙偱丄倛俥俤偑侾侽侽攞側傜丄僐儗僋僞揹棳偼侾倣俙偱偡丅
壓恾嵍偱偼俆倁偺僐儗僋僞揹埑偑丄塃偱偼俋倁偲曄壔偟偰偄傑偡偑丄僐儗僋僞揹棳偼嵍塃嫟偵侾倣俙偱堦掕偱偡丅偙偺偙偲傪乽掕揹棳摿惈乿偲屇傃傑偟偨丅
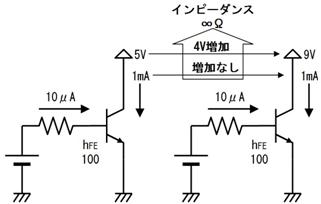
偮傑傝丄乽奜晹偐傜揹埑偺曄壔乮岎棳揹埑乯傪壛偊偰傕丄揹棳偑曄壔偟側偄乮岎棳揹棳偑棳傟側偄乯乿偲偄偆帠偱偡偐傜丄岎棳偺掞峈抣乮僀儞僺乕僟儞僗乯偼丄柍尷偵戝偒偄帠偑暘偐傝傑偡丅
僀儞僺乕僟儞僗偼掞峈偲摨條偵丄揹埑亐揹棳偱偡偐傜丄師偺寁嶼偐傜傕丄僀儞僺乕僟儞僗偑柍尷偵戝偒偔側傞帠偑暘傝傑偡丅
僀儞僺乕僟儞僗
亖 岎棳揹埑
亐 岎棳揹棳
亖 係倁曄壔
亐 侽倣俙曄壔
亖 亣
僐儗僋僞偺僀儞僺乕僟儞僗偼亣偵戝偒偄乮岎棳傪捠偝側偄乯偺偱丄壓恾偺傛偆偵乽僐儗僋僞偼僀儞僺乕僟儞僗揑偵偼抐慄偟偰偄傞乿偲峫偊傟偽丄壓恾偺庤弴偱僐儗僋僞夞楬偺僀儞僺乕僟儞僗傪娙扨偵媮傔傞偙偲偑偱偒傑偡丅
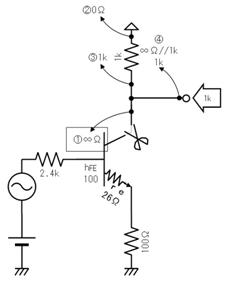
侾俇.侾. 妋擣
忋恾傪尒偰壓昞傪彂偒崬傫偱偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
廳梫
|
僐儗僋僞偺僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘇
|
侾倠兌偺忋懁偐傜揹尮傪尒傞偲僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘊
|
侾倠兌偺壓懁偐傜揹尮傪尒傞偲僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘋
|
弌椡抂巕偐傜夞楬傪尒傞偲丄嘆偲嘊偑暲楍偵尒偊偰丄
|
倠兌
|
侾俇.俀. 摎
忋恾傪尒偰壓昞傪彂偒崬傫偱偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
廳梫
|
僐儗僋僞偺僀儞僺乕僟儞僗偼丄
|
亣兌
|
|
嘇
|
侾倠兌偺忋懁偐傜揹尮傪尒傞偲僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘊
|
侾倠兌偺壓懁偐傜揹尮傪尒傞偲僀儞僺乕僟儞僗偼丄
|
侾倠兌
|
|
嘋
|
弌椡抂巕偐傜夞楬傪尒傞偲丄嘆偲嘊偑暲楍偵尒偊偰丄
|
侾倠兌
|
壓恾偺傛偆偵丄椺偊偽丄倛俥俤偑侾侽侽攞偺偲偒丄僄儈僢僞揹棳偑侾倣俙側傜儀乕僗揹棳偼侾侽兪俙乮壓恾嵍乯丄僄儈僢僞揹棳偑俀倣俙側傜儀乕僗揹棳偼俀侽兪俙乮壓恾塃乯偱偡丅
壓恾嵍偱偼侾丏俈倁偺儀乕僗揹埑偑丄塃偱偼俀丏俈倁偲丄侾倁曄壔偟偰偄傑偡丅偙傟偵傛偭偰丄僄儈僢僞偺揹棳偼侾倣俙偐傜俀倣俙偵曄壔偟偰偄傑偡偑丄儀乕僗揹棳偼僄儈僢僞揹棳偺侾乛倛俥俤偱偡偐傜丄侾侽兪俙偐傜俀侽兪俙偵曄壔偟偰偄傑偡丅
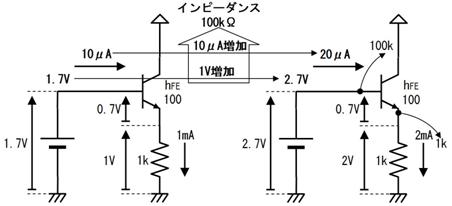
偮傑傝丄儀乕僗偺揹埑傪侾倁曄壔偝偣傞乮岎棳侾倁傪壛偊傞乯偲丄儀乕僗揹棳偑侾侽兪俙曄壔偡傞乮岎棳揹棳偑侾侽兪俙棳傟傞乯偲暘偐傝傑偡丅偱偡偐傜丄師偺寁嶼偺傛偆偵丄儀乕僗偺僀儞僺乕僟儞僗偼侾倁亐侾侽兪俙偱丄侾侽侽倠兌偲暘偐傝傑偡丅
儀乕僗偺僀儞僺乕僟儞僗
亖 岎棳揹埑
亐 岎棳揹棳
亖
侾倁曄壔 亐 侾侽兪俙曄壔
亖 侾侽侽倠兌
儀乕僗偺揹棳偼僄儈僢僞偺揹棳偺侾乛倛俥俤偵彫偝偔側傞偺偱丄僄儈僢僞乮偐傜傾乕僗傪尒偨帪乯偺僀儞僺乕僟儞僗乮忋恾偱偼侾倠兌乯偑丄倛俥俤攞乮忋恾偱偼侾侽侽攞乯偵崅偔側偭偰儀乕僗偵尰傟傞乮忋恾偱偼侾侽侽倠兌乯偲峫偊傞偙偲偑偱偒傑偡丅
儀乕僗偺揹棳
亖 僄儈僢僞揹棳
亐 倛俥俤
儀乕僗偺僀儞僺乕僟儞僗
亖 僄儈僢僞偺僀儞僺乕僟儞僗
亊 倛俥俤
傛傝徻偟偔偼師偺傛偆偵媮傔傜傟傑偡丄
倅倕亖倴倕亐倝倕
倴倐亖倴倕
倝倕亖倝倐亊倛俥俤
倅倐亖倴倐亐倝倐亖倴倕亐倝倐亊倛俥俤亖倅倕亊倛俥俤
儀乕僗偺僀儞僺乕僟儞僗偼僄儈僢僞偺僀儞僺乕僟儞僗偺倛俥俤攞偵側傞偺偱丄儀乕僗夞楬偺僀儞僺乕僟儞僗偼丄倰倕傕攝椂偟偰丄壓恾偺庤弴偱傪娙扨偵媮傔傞偙偲偑偱偒傑偡丅
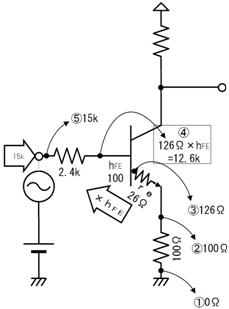
侾俈.侾. 妋擣
忋恾傪尒偰壓昞傪彂偒崬傫偱偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
侾侽侽兌偺壓懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘇
|
侾侽侽兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘊
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗乮僄儈僢僞偺慡僀儞僺乕僟儞僗乯偼丄
|
兌
|
|
嘋
廳梫
|
倛俥俤傪侾侽侽偲偡傞偲丄儀乕僗偺僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘍
|
擖椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
侾俈.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
侾侽侽兌偺壓懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘇
|
侾侽侽兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
侾侽侽兌
|
|
嘊
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗乮僄儈僢僞偺慡僀儞僺乕僟儞僗乯偼丄
|
侾俀俇兌
|
|
嘋
廳梫
|
倛俥俤傪侾侽侽偲偡傞偲丄儀乕僗偺僀儞僺乕僟儞僗偼丄
|
侾俀丏俇倠兌
|
|
嘍
|
擖椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
|
侾俆倠兌
|
儀乕僗偐傜傒傞偲僄儈僢僞偺僀儞僺乕僟儞僗偑倛俥俤攞偵側傝傑偟偨丅媡偵丄僄儈僢僞偐傜尒傞偲儀乕僗偺僀儞僺乕僟儞僗偑侾乛倛俥俤偵側傝傑偡丅偦偺偨傔丄僄儈僢僞夞楬偺僀儞僺乕僟儞僗偼丄倰倕傕攝椂偟偰丄壓恾偺庤弴偱傪娙扨偵媮傔傞偙偲偑偱偒傑偡丅
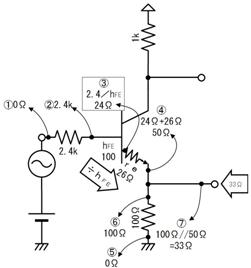
侾俉.侾. 妋擣
忋恾傪尒偰壓昞傪彂偒崬傫偱偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
乮揹抮傗岎棳尮偼僀儞僺乕僟儞僗偼偲偰傕掅偄偐傜丄乯
|
兌
|
|
嘇
|
儀乕僗偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘊
廳梫
|
倛俥俤傪侾侽侽偲偡傞偲丄倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘋
|
僄儈僢僞偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
乮倰倕偑俀俇兌偩偐傜丄乯
|
兌
|
|
嘍
|
侾侽侽兌偺壓懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘐
|
侾侽侽兌偺忋懁偑傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘑
|
弌椡抂巕偐傜夞楬慡懱傪尒偨僀儞僺乕僟儞僗偼丄
乮嘋偲嘐偑暲楍偵尒偊傞偐傜丄乯
|
兌
|
侾俉.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
乮揹抮傗岎棳尮偼僀儞僺乕僟儞僗偼偲偰傕掅偄偐傜丄乯
|
侽兌
|
|
嘇
|
儀乕僗偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
|
俀丏係倠兌
|
|
嘊
廳梫
|
倛俥俤傪侾侽侽偲偡傞偲丄倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
|
俀係兌
|
|
嘋
|
僄儈僢僞偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
乮倰倕偑俀俇兌偩偐傜丄乯
|
俆侽兌
|
|
嘍
|
侾侽侽兌偺壓懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘐
|
侾侽侽兌偺忋懁偑傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
侾侽侽兌
|
|
嘑
|
弌椡抂巕偐傜夞楬慡懱傪尒偨僀儞僺乕僟儞僗偼丄
乮嘋偲嘐偑暲楍偵尒偊傞偐傜丄乯
|
俁俁兌
|
偙傟傑偱偺愢柧傪傑偲傔傞偲丄僩儔儞僕僗僞偺僀儞僺乕僟儞僗偼壓恾偺傛偆偵偟偰媮傔傞偙偲偑偱偒傑偡丅
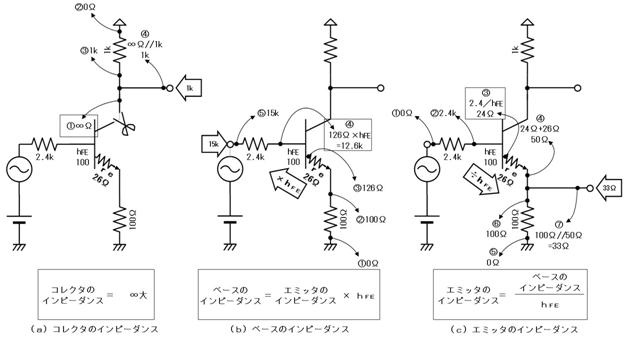
侾俉.俁. 楙廗
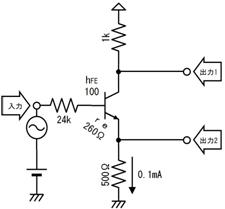
忋恾偺夞楬偺擖椡丄弌椡侾丄弌椡俀偺僀儞僺乕僟儞僗傪丄壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜摎偊偰偔偩偝偄丅乮偨偩偟丄擖椡僀儞僺乕僟儞僗偼丄愙懕偝傟偨揹埑尮偲怣崋尮偺僀儞僺乕僟儞僗傪娷傔偢偵摎偊偰偔偩偝偄乯
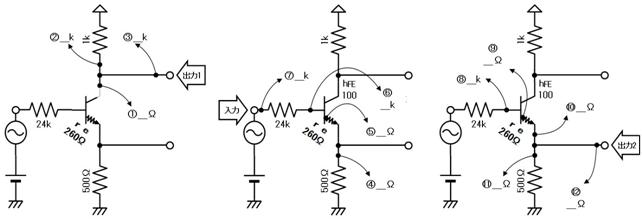
|
斣崋
|
幙栤
|
抣
|
|
|
弌椡侾偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘆
廳梫
|
僐儗僋僞偺僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘇
|
侾倠兌偺壓偐傜揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘊
|
弌椡侾抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮侾倠兌偲亣兌偑暲楍偵尒偊偰丄乯
|
倠兌
|
|
|
擖椡偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘋
|
俆侽侽兌偺忋偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘍
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄乮倰倕偑俀俇侽兌偩偐傜丄乯
|
兌
|
|
嘐
廳梫
|
儀乕僗偺僀儞僺乕僟儞僗偼丄倛俥俤偑侾侽侽偩偐傜丄
|
倠兌
|
|
嘑
|
擖椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
|
弌椡俀偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘒
|
俀係倠兌偺塃懁偐傜丄嵍傪尒偨僀儞僺乕僟儞僗偼丄
乮揹抮傗怣崋尮偺僀儞僺乕僟儞僗偼掅偄偐傜乯
|
倠兌
|
|
嘓
廳梫
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄乮倛俥俤偑侾侽侽偩偐傜丄乯
|
兌
|
|
嘔
|
僄儈僢僞偺僀儞僺乕僟儞僗偼丄乮倰倕偑俀俇侽兌偩偐傜丄乯
|
兌
|
|
嘕
|
俆侽侽兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘖
|
弌椡俀抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮俆侽侽兌偲僄儈僢僞偑暲楍偵尒偊傞偐傜丄乯
|
兌
|
侾俉.係. 摎
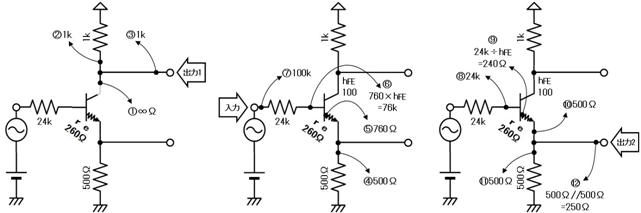
|
斣崋
|
幙栤
|
抣
|
|
|
弌椡侾偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘆
廳梫
|
僐儗僋僞偺僀儞僺乕僟儞僗偼丄
|
亣兌
|
|
嘇
|
侾倠兌偺壓偐傜揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
侾倠兌
|
|
嘊
|
弌椡侾抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮侾倠兌偲亣兌偑暲楍偵尒偊偰丄乯
|
侾倠兌
|
|
|
擖椡偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘋
|
俆侽侽兌偺忋偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
俆侽侽兌
|
|
嘍
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄乮倰倕偑俀俇侽兌偩偐傜丄乯
|
俈俇侽兌
|
|
嘐
廳梫
|
儀乕僗偺僀儞僺乕僟儞僗偼丄倛俥俤偑侾侽侽偩偐傜丄
|
俈俇倠兌
|
|
嘑
|
擖椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
|
侾侽侽倠兌
|
|
|
弌椡俀偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘒
|
俀係倠兌偺塃懁偐傜丄嵍傪尒偨僀儞僺乕僟儞僗偼丄
乮揹抮傗怣崋尮偺僀儞僺乕僟儞僗偼掅偄偐傜乯
|
俀係倠兌
|
|
嘓
廳梫
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄乮倛俥俤偑侾侽侽偩偐傜丄乯
|
俀係侽兌
|
|
嘔
|
僄儈僢僞偺僀儞僺乕僟儞僗偼丄乮倰倕偑俀俇侽兌偩偐傜丄乯
|
俆侽侽兌
|
|
嘕
|
俆侽侽兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
俆侽侽兌
|
|
嘖
|
弌椡俀抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮俆侽侽兌偲僄儈僢僞偑暲楍偵尒偊傞偐傜丄乯
|
俀俆侽兌
|
侾俉.俆. 楙廗
忋偺楙廗偱埖偭偨憹暆婍俙乮弌椡僀儞僺乕僟儞僗侾倠兌乯偑丄壓恾偵帵偡傛偆偵丄柍晧壸帪乮側偵傕宷偑側偄偲偒乯俀侽俀倣倁偺岎棳揹埑傪弌椡偟偰偄傑偟偨丅偙傟偵丄廫暘戝偒側僐儞僨儞僒傪夘偟偰丄摨偠憹暆婍俛乮擖椡僀儞僺乕僟儞僗侾侽侽倠兌乯傪宷偖偲丄憹暆婍俙偺弌椡乽偁乿偺岎棳弌椡揹埑偼壗倁偵尭傝傑偡偐丅扐偟丄憹暆婍俛偺摦嶌偼乮僶僀傾僗梡揹抮傪庢傝彍偄偰傕乯楙廗偱埖偭偨忬懺偐傜曄壔偟側偄偲峫偊傑偡丅
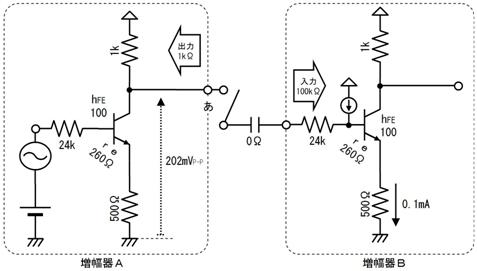
侾俉.俇. 摎
憹暆婍偺擖椡僀儞僺乕僟儞僗乮侾侽侽倠兌乯偲弌椡僀儞僺乕僟儞僗乮侾倠兌乯偑暘偐偭偰偄傞偺偱丄壓恾偺傛偆偵峫偊偰丄俀侽侽倣倁偵尭傞丅
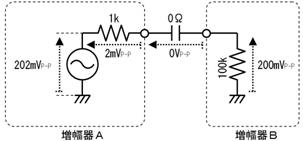
僐儞僨儞僒偺梕検偼乽廫暘戝偒偄乿偲峫偊偰寁嶼偟偰偒傑偟偨丅偙偙偱偼乽廫暘戝偒偄乿偲峫偊傞偨傔偵偼丄僐儞僨儞僒偺梕検傪偄偔傜偵偡傟偽椙偄偐傪愢柧偟傑偡丅
傑偢丄壓恾偺俠俼夞楬偵岎棳偑壛傢傞偲丄僐儞僨儞僒偵棳傟傞揹棳偼丄廃攇悢偑侾俇侽俫倸傛傝掅偔側傞偲尭彮偟傑偡丅
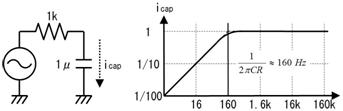
揹棳偑尭彮偟巒傔傞廃攇悢偼丄婛偵愢柧偟偨乽幷抐廃攇悢乿倖俠偱丄師偺傛偆偵寁嶼偱偒傑偡丅
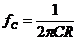
忋偺椺偱偼丄=1/2/PI()/1E-6/1E3
壓恾偺傛偆偵夞楬偑暋嶨側応崌傕丄僐儞僨儞僒偐傜尒偨僀儞僺乕僟儞僗傪媮傔偰丄幷抐廃攇悢傪寁嶼偱偒傑偡丅
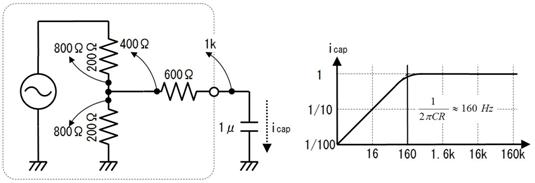
忋偺椺偱傕丄僐儞僨儞僒偐傜尒偨僀儞僺乕僟儞僗偑侾倠兌偱偡偐傜丄幷抐廃攇悢偼侾俇侽俫倸偱偡丅
偝偰丄幷抐廃攇悢偼憹暆婍偱巊梡偡傞嵟掅偺廃攇悢傪栚埨偵慖傃傑偡丅僐儞僨儞僒偵棳傟傞揹棳偼幷抐廃攇悢偺庤慜偐傜掅壓傪巒傔丄壓恾偵帵偡傛偆偵丄巊梡偡傞廃攇悢偑幷抐廃攇悢偲摨偠偱傕丄僐儞僨儞僒偺揹棳偼俁妱掱搙尭彮偟傑偡丅偦偟偰丄巊梡偡傞廃攇悢偑幷抐廃攇悢偺係乣俆攞偵崅偗傟偽丄揹棳偺尭彮偼杦偳柍帇偱偒傑偡丅
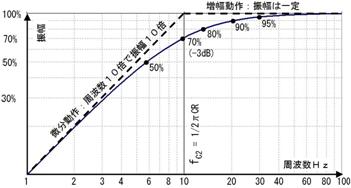
偨偲偊怳暆偺尭彮偑俁妱偱傕丄偨偲偊偽擖椡丄僄儈僢僞丄弌椡偲俁偮偺僐儞僨儞僒偑巊傢傟偰偄傞偲丄俈侽亾亊俈侽亾亊俈侽亾亖俁係亾偲丄怳暆偼敿暘埲壓偵尭彮偟傑偡丅偱偡偐傜丄怳暆偺尭彮偑杦偳柍帇偱偒傞傛偆偵丄巊梡偡傞廃攇悢傪幷抐廃攇悢偺係乣俆攞偵乮幷抐廃攇悢傪巊梡偡傞廃攇悢偺係乣俆暘偺侾偵乯慖傇応崌偑懡偄偱偡丅
椺偊偽丄憹暆偡傞嵟掅偺廃攇悢傪侾侽侽俫倸偲偟丄怳暆偺尭彮偑柍帇偱偒傞傛偆偵偡傞応崌偼丄幷抐廃攇悢傪乮侾侽侽俫倸偺係乣俆暘偺侾偺乯俀侽俫倸掱搙偵愝掕偟傑偡丅
幷抐廃攇悢傪愝掕偟偨傜丄師偵夞楬傪専摙偟偰僐儞僨儞僒偺梕検傪寛掕偟傑偡丅椺偊偽壓恾乮倎乯偼丄憹暆婍偺弌椡傪僐儞僨儞僒傪捠偠偰晧壸偵愙懕偟偨夞楬偱偡丅偙偺夞楬偱偼丄壓恾乮倐乯偵帵偡傛偆偵丄弌椡僀儞僺乕僟儞僗偺侾倠兌偲丄晧壸僀儞僺乕僟儞僗偺侾倠兌偼丄憃曽偲傕僐儞僨儞僒偲捈楍偵愙懕偝傟偰偄傑偡丅偙偺偨傔丄僐儞僨儞僒偐傜尒偨僀儞僺乕僟儞僗偼壓恾乮們乯偺傛偆偵俀倠兌偲側傝丄幷抐廃攇悢傪俀侽俫倸偲偡傟偽丄僐儞僨儞僒偺梕検偼=1/2/PI()/20/2E3偲寁嶼偟偰丄4兪俥偲暘偐傝傑偡丅
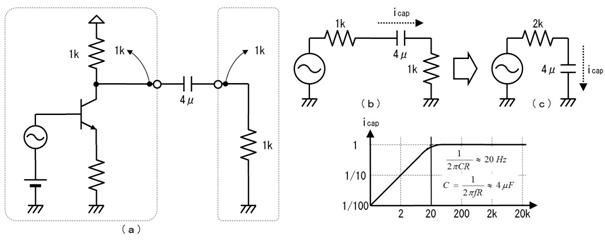
偳偺傛偆側僀儞僺乕僟儞僗偺晧壸傪愙懕偡傞偐暘偐傜側偄憹暆夞楬偺応崌偼丄壓恾乮倐乯偺傛偆偵乮嵟埆偺応崌偲偟偰乯侽兌偺晧壸傪愙懕偟偨偲峫偊偰丄僐儞僨儞僒偐傜尒偨僀儞僺乕僟儞僗傪壓恾乮倐乯偺傛偆偵侾倠兌偲偟偰=1/2/PI()/20/1E3偲寁嶼偟丄僐儞僨儞僒偺梕検傪俉兪俥偲偟傑偡丅
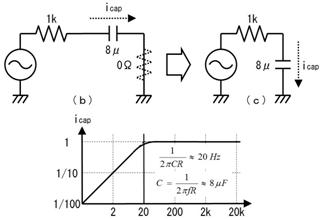
偙偺寁嶼曽朄偼弌椡僐儞僨儞僒偵傕丄擖椡僐儞僨儞僒偵傕巊梡偡傞偙偲偑偱偒傑偡丅
偳偺傛偆側擖椡傪愙懕偡傞偐暘偐傜側偄憹暆夞楬偺応崌偼丄壓恾乮倐乯偺傛偆偵乮嵟埆偺応崌偲偟偰乯侽兌偺怣崋尮傪愙懕偟偨偲峫偊偰丄僐儞僨儞僒偐傜尒偨僀儞僺乕僟儞僗傪壓恾乮倐乯偺傛偆偵侾倠兌偲偟偰=1/2/PI()/20/1E3偲寁嶼偟丄僐儞僨儞僒偺梕検傪俉兪俥偲偟傑偡丅
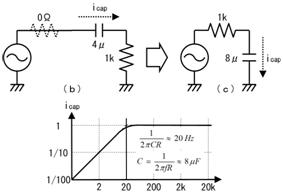
椺偊偽壓恾偺傛偆側丄僄儈僢僞僶僀僷僗僐儞僨儞僒偺応崌偼丄僐儞僨儞僒偐傜偼乮倎乯偺僀儞僺乕僟儞僗俀侽侽兌偲丄乮倐乯偺僀儞僺乕僟儞僗乮俉侽侽兌乯偑暲楍偵尒偊傑偡丅
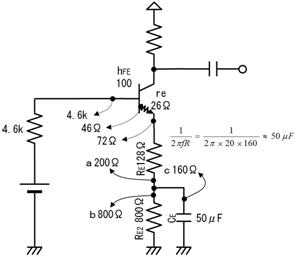
偱偡偐傜丄僐儞僨儞僒偐傜尒偨夞楬偺僀儞僺乕僟儞僗偼侾俇侽兌偱偡丅幷抐廃攇悢偑俀侽俫倸偱偁傟偽丄=1/2/PI()/20/160偲寁嶼偟偰丄僐儞僨儞僒偺梕検偼俆侽兪俥偲暘偐傝傑偡丅
俀侾.侾. 楙廗
壓恾偺傛偆偵奣偹僀儞僺乕僟儞僗専摙傪廔偊偨憹暆婍偑偁傝傑偡丅忋恾傪嶲峫偵壓昞偵彂偒崬傒丄擖弌椡僐儞僨儞僒偲僄儈僢僞僶僀僷僗僐儞僨儞僒偺梕検傪寛掕偟偰偔偩偝偄丅憹暆婍偱巊梡偡傞嵟掅偺廃攇悢偼俀侽俫倸偱丄幷抐廃攇悢偼偦偺係暘偺侾偺俆俫倸偲愝掕偟傑偡丅
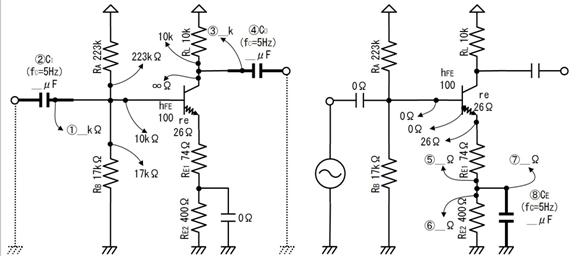
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡僐儞僨儞僒偺塃懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄乮俼俙丄俼俛丄儀乕僗丄偑暲楍偵尒偊偰丄乯
|
倠兌
|
|
嘇
|
幷抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄擖椡僐儞僨儞僒俠俬偺梕検偼丄
|
兪俥
|
|
嘊
|
弌椡僐儞僨儞僒偺嵍懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄乮俼俴偲僐儗僋僞偑暲楍偵尒偊偰丄乯
|
倠兌
|
|
嘋
|
幷抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄弌椡僐儞僨儞僒俠俷偺梕検偼丄
|
兪俥
|
|
嘍
|
俼俤侾偺壓懁偐傜忋傪尒偨僀儞僺乕僟儞僗偼丄
乮倰倕乮俀俇兌乯偲俼俤侾乮俈係兌乯偑捈楍偵尒偊偰丄乯
|
兌
|
|
嘐
|
俼俤俀偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘑
|
僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄乮忋偺嘍偲嘐偑暲楍偵尒偊偰丄乯
|
兌
|
|
嘒
|
幷抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偺梕検偼丄
|
兪俥
|
俀侾.俀. 摎
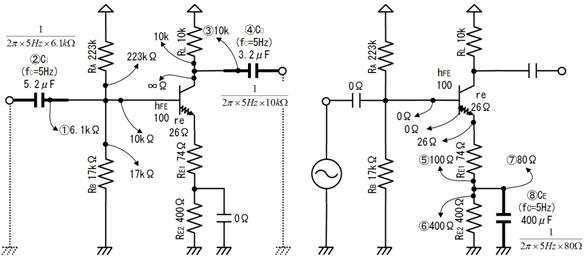
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡僐儞僨儞僒偺塃懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄乮俼俙丄俼俛丄儀乕僗丄偑暲楍偵尒偊偰丄乯
|
俇丏侾倠兌
|
|
嘇
|
幷抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄擖椡僐儞僨儞僒俠俬偺梕検偼丄
=1/2/PI()/5/6.1E3
|
俆丏俀兪俥
|
|
嘊
|
弌椡僐儞僨儞僒偺嵍懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄乮俼俴偲僐儗僋僞偑暲楍偵尒偊偰丄乯
|
侾侽倠兌
|
|
嘋
|
幷抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄弌椡僐儞僨儞僒俠俷偺梕検偼丄
=1/2/PI()/5/10E3
|
俁丏俀兪俥
|
|
嘍
|
俼俤侾偺壓懁偐傜忋傪尒偨僀儞僺乕僟儞僗偼丄
乮倰倕乮俀俇兌乯偲俼俤侾乮俈係兌乯偑捈楍偵尒偊偰丄乯
|
侾侽侽兌
|
|
嘐
|
俼俤俀偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
俉侽侽兌
|
|
嘑
|
僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄乮忋偺嘍偲嘐偑暲楍偵尒偊偰丄乯
|
俉侽兌
|
|
嘒
|
幷抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偺梕検偼丄
=1/2/PI()/5/80
|
係侽侽兪俥
|
壓恾偼擖弌椡乮寢崌乛僇僢僾儕儞僌乯僐儞僨儞僒丄暘埑僶僀傾僗夞楬丄僄儈僢僞僶僀僷僗僐儞僨儞僒傪旛偊偨昗弨揑側僩儔儞僕僗僞憹暆婍偱偡丅偙傟傑偱偵楙廗偟偨撪梕傪妶梡偟偰丄壓偺夞楬傪専摙偟偰傒傑偟傚偆丅乮楙廗偺栚揑偱僄儈僢僞偐傜傕弌椡傪庢傝弌偟偰偄傑偡乯
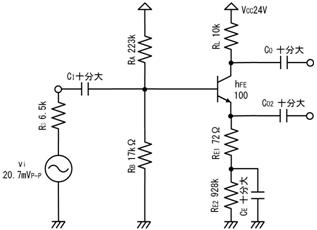
忋恾偺夞楬傪捈棳専摙偟偰夞楬偺徚旓揹棳傪媮傔丄僀儞僺乕僟儞僗専摙丄岎棳専摙偟偰丄俀偮偺弌椡抂巕偺弌椡僀儞僺乕僟儞僗丄弌椡揹埑丄巊梡偡傞僐儞僨儞僒偺抣傪媮傔傑偡丅
俀俀.侾. 楙廗
壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜丄捈棳専摙偟偰夞楬偺徚旓揹棳傪媮傔偰偔偩偝偄丅
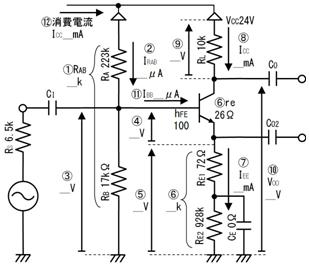
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俼俙偲俼俛偺捈楍崌惉掞峈偼丄
|
倠兌
|
|
嘇
|
俼俙偲俼俛偵棳傟傞揹棳丄俬俼俙俛偼丄
|
兪俙
|
|
嘊
|
俼俛偺椉抂揹埑偼丄
|
倁
|
|
嘋
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘍
|
俼俤侾偲俼俤俀偵壛傢傞揹埑偺崌寁偼丄
|
倁
|
|
嘐
|
俼俤侾偲俼俤俀偺捈楍崌惉掞峈偼丄
|
倠兌
|
|
嘑
|
僄儈僢僞僶僀傾僗揹棳俬俤俤偼丄
|
倣俙
|
|
嘒
|
僐儗僋僞僶僀傾僗揹棳俬俠俠偼丄
|
倣俙
|
|
嘓
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
倁
|
|
嘔
|
弌椡僶僀傾僗揹埑倁俷俷偼丄
|
倁
|
|
嘕
|
儀乕僗僶僀傾僗揹棳俬俛俛偼丄
|
兪俙
|
|
嘖
|
夞楬偺徚旓揹棳偼丄乮嘒偲嘇偐傜丄乯
|
倣俙
|
俀俀.俀. 摎
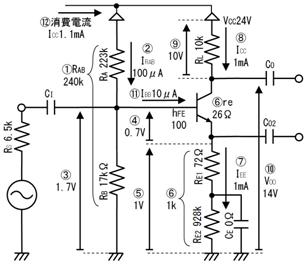
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俼俙偲俼俛偺捈楍崌惉掞峈偼丄
|
俀係侽倠兌
|
|
嘇
|
俼俙偲俼俛偵棳傟傞揹棳丄俬俼俙俛偼丄
|
侾侽侽兪俙
|
|
嘊
|
俼俛偺椉抂揹埑偼丄
|
侾丏俈倁
|
|
嘋
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘍
|
俼俤侾偲俼俤俀偵壛傢傞揹埑偺崌寁偼丄
|
侾倁
|
|
嘐
|
俼俤侾偲俼俤俀偺捈楍崌惉掞峈偼丄
|
侾倠兌
|
|
嘑
|
僄儈僢僞僶僀傾僗揹棳俬俤俤偼丄
|
侾倣俙
|
|
嘒
|
僐儗僋僞僶僀傾僗揹棳俬俠俠偼丄
|
侾倣俙
|
|
嘓
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
侾侽倁
|
|
嘔
|
弌椡僶僀傾僗揹埑倁俷俷偼丄
|
侾係倁
|
|
嘕
|
儀乕僗僶僀傾僗揹棳俬俛俛偼丄
|
侾侽兪俙
|
|
嘖
|
夞楬偺徚旓揹棳偼丄乮嘒偲嘇偐傜丄乯
|
侾丏侾倣俙
|
俀俀.俁. 楙廗
壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜丄儀乕僗懁偲僐儗僋僞懁偺僀儞僺乕僟儞僗傪専摙偟偰偔偩偝偄丅
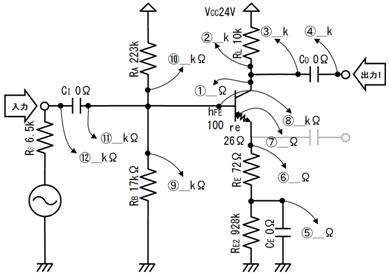
|
斣崋
|
幙栤
|
抣
|
|
|
弌椡侾乮僐儗僋僞懁乯偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘆
|
僐儗僋僞偺僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘇
|
侾侽倠兌偺壓偐傜揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘊
|
俠俷偺嵍懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮侾侽倠兌偲亣兌偑暲楍偵尒偊偰丄乯
|
倠兌
|
|
嘋
|
弌椡侾抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俷偑廫暘戝偒偄偐傜丄乯
|
倠兌
|
|
|
擖椡偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘍
|
俋俀俉兌忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俤偑廫暘戝偒偄偐傜丄乯
|
兌
|
|
嘐
|
俈俀兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘑
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄乮倰倕偑俀俇兌偩偐傜丄乯
|
兌
|
|
嘒
|
儀乕僗偺僀儞僺乕僟儞僗偼丄倛俥俤偑侾侽侽偩偐傜丄
|
倠兌
|
|
嘓
|
侾俈倠偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘔
|
俀俀俁倠偺壓懁偐傜揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘕
|
俠俬偺塃懁偐傜塃傪尒偨僀儞僺乕僟儞僗偼丄
乮嘒嘓嘔偑暲楍偵尒偊偰丄乯
|
倠兌
|
|
嘖
|
擖椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俬偑廫暘戝偒偄偐傜丄乯
|
倠兌
|
俀俀.係. 摎
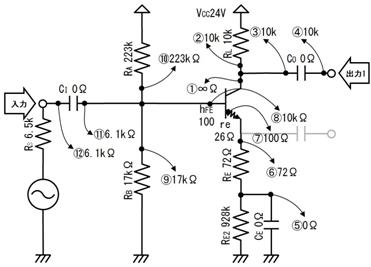
|
斣崋
|
幙栤
|
抣
|
|
|
弌椡侾乮僐儗僋僞懁乯偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘆
|
僐儗僋僞偺僀儞僺乕僟儞僗偼丄
|
亣兌
|
|
嘇
|
侾侽倠兌偺壓偐傜揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
侾侽倠兌
|
|
嘊
|
俠俷偺嵍懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮侾侽倠兌偲亣兌偑暲楍偵尒偊偰丄乯
|
侾侽倠兌
|
|
嘋
|
弌椡侾抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俷偑廫暘戝偒偄偐傜丄乯
|
侾侽倠兌
|
|
|
擖椡偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘍
|
俋俀俉兌忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俤偑廫暘戝偒偄偐傜丄乯
|
侽兌
|
|
嘐
|
俈俀兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
俈俀兌
|
|
嘑
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄乮倰倕偑俀俇兌偩偐傜丄乯
|
侾侽侽兌
|
|
嘒
|
儀乕僗偺僀儞僺乕僟儞僗偼丄倛俥俤偑侾侽侽偩偐傜丄
|
侾侽倠兌
|
|
嘓
|
侾俈倠偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
侾俈倠兌
|
|
嘔
|
俀俀俁倠偺壓懁偐傜揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
俀俀俁倠兌
|
|
嘕
|
俠俬偺塃懁偐傜塃傪尒偨僀儞僺乕僟儞僗偼丄
乮嘒嘓嘔偑暲楍偵尒偊偰丄乯
|
俇丏侾倠兌
|
|
嘖
|
擖椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俬偑廫暘戝偒偄偐傜丄乯
|
俇丏侾倠兌
|
俀俀.俆. 楙廗
壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜丄僄儈僢僞懁偺僀儞僺乕僟儞僗傪専摙偟偰偔偩偝偄丅
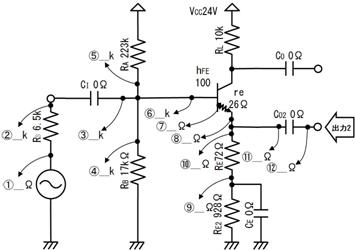
|
斣崋
|
幙栤
|
抣
|
|
|
弌椡俀乮僄儈僢僞懁乯偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘆
|
怣崋尮偺僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘇
|
俇丏俆倠偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘊
|
俠俬偺塃懁偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俬偑廫暘戝偒偄偐傜乯
|
倠兌
|
|
嘋
|
侾俈倠偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘍
|
俀俀俁倠偺壓懁偐傜揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘐
|
儀乕僗偐傜嵍懁傪尒偨僀儞僺乕僟儞僗偼丄
乮嘊嘋嘍偺俁偮偑暲楍偵尒偊偰丄乯
|
倠兌
|
|
嘑
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄乮倛俥俤偑侾侽侽偩偐傜丄乯
|
兌
|
|
嘒
|
僄儈僢僞偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘓
|
俋俀俉兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俤偑廫暘戝偒偄偐傜丄乯
|
兌
|
|
嘔
|
俈俀兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘕
|
俠俷俀偺嵍懁偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
乮嘒偲嘔偑暲楍偵尒偊偰丄乯
|
兌
|
|
嘖
|
弌椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俷俀偼廫暘戝偒偄偐傜丄乯
|
兌
|
俀俀.俇. 摎
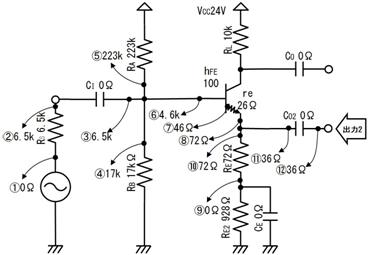
|
斣崋
|
幙栤
|
抣
|
|
|
弌椡俀乮僄儈僢僞懁乯偺僀儞僺乕僟儞僗傪峫偊傑偡
|
亅
|
|
嘆
|
怣崋尮偺僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘇
|
俇丏俆倠偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
俇丏俆倠兌
|
|
嘊
|
俠俬偺塃懁偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俬偑廫暘戝偒偄偐傜乯
|
俇丏俆倠兌
|
|
嘋
|
侾俈倠偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
侾俈倠兌
|
|
嘍
|
俀俀俁倠偺壓懁偐傜揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
俀俀俁倠兌
|
|
嘐
|
儀乕僗偐傜嵍懁傪尒偨僀儞僺乕僟儞僗偼丄
乮嘊嘋嘍偺俁偮偑暲楍偵尒偊偰丄乯
|
係丏俇倠兌
|
|
嘑
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄乮倛俥俤偑侾侽侽偩偐傜丄乯
|
係俇兌
|
|
嘒
|
僄儈僢僞偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
|
俈俀兌
|
|
嘓
|
俋俀俉兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俤偑廫暘戝偒偄偐傜丄乯
|
侽兌
|
|
嘔
|
俈俀兌偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
俈俀兌
|
|
嘕
|
俠俷俀偺嵍懁偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
乮嘒偲嘔偑暲楍偵尒偊偰丄乯
|
俁俇兌
|
|
嘖
|
弌椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮俠俷俀偼廫暘戝偒偄偐傜丄乯
|
俁俇兌
|
俀俀.俈. 楙廗
壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜丄岎棳専摙偟偰岎棳弌椡揹埑傪媮傔偰偔偩偝偄丅
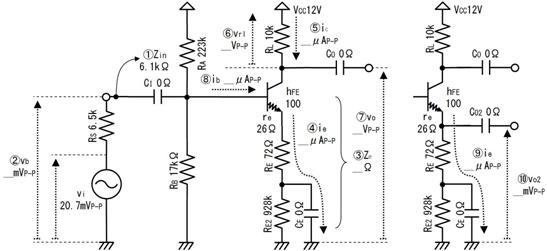
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
憹暆婍偺擖椡僀儞僺乕僟儞僗倅倝値偼丄
乮偡偱偵媮傔偨偲偍傝丄乯
|
俇丏侾倠兌
|
|
嘇
|
怣崋揹埑偑俀侽丏俈倣俙俹亅俹丄怣崋尮僀儞僺乕僟儞僗俼俽偑俇丏俆倠兌偩偐傜丄憹暆婍偺擖椡抂巕乮敀娵乯偵壛傢傞岎棳揹埑偼丄
|
倣倁俹亅俹
|
|
嘊
|
僄儈僢僞懁僀儞僺乕僟儞僗偺崌寁偼丄
|
兌
|
|
嘋
|
僄儈僢僞怣崋揹棳倝倕偼丄
|
兪俙俹亅俹
|
|
嘍
|
僐儗僋僞怣崋揹棳倝們偼丄
|
兪俙俹亅俹
|
|
嘐
|
晧壸掞峈俼俴偺椉抂怣崋揹埑倴倰倢偼丄
|
倁俹亅俹
|
|
嘑
|
弌椡怣崋揹埑倴倧偼丄
|
倁俹亅俹
|
|
嘒
|
儀乕僗怣崋揹棳倝倐偼丄
|
兪俙俹亅俹
|
|
嘓
|
崱堦搙丄僄儈僢僞怣崋揹棳偼丄
|
兪俙俹亅俹
|
|
嘔
|
僄儈僢僞懁弌椡抂巕偺弌椡怣崋揹埑倴倧俀偼丄
侾侽侽兪俙俹亅俹亊俈俀兌亖俈丏俀倣倁俹亅俹
|
倣倁俹亅俹
|
俀俀.俉. 摎
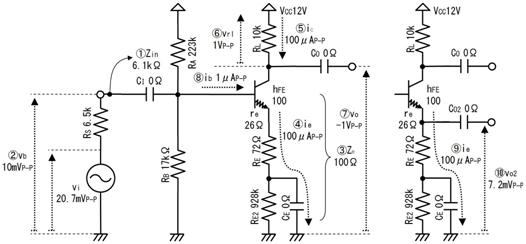
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
憹暆婍偺擖椡僀儞僺乕僟儞僗倅倝値偼丄
|
俇丏侾倠兌
|
|
嘇
|
怣崋揹埑偑俀侽丏俈倣俙俹亅俹丄怣崋尮僀儞僺乕僟儞僗俼俽偑俇丏俆倠兌偩偐傜丄憹暆婍偺擖椡抂巕乮敀娵乯偵壛傢傞岎棳揹埑偼丄
|
侾侽倣倁俹亅俹
|
|
嘊
|
僄儈僢僞懁僀儞僺乕僟儞僗偺崌寁偼丄
|
侾侽侽兌
|
|
嘋
|
僄儈僢僞怣崋揹棳倝倕偼丄
|
侾侽侽兪俙俹亅俹
|
|
嘍
|
僐儗僋僞怣崋揹棳倝們偼丄
|
侾侽侽兪俙俹亅俹
|
|
嘐
|
晧壸掞峈俼俴偺椉抂怣崋揹埑倴倰倢偼丄
|
侾倁俹亅俹
|
|
嘑
|
弌椡怣崋揹埑倴倧偼丄
|
亅侾倁俹亅俹
|
|
嘒
|
儀乕僗怣崋揹棳倝倐偼丄
|
侾兪俙俹亅俹
|
|
嘓
|
崱堦搙丄僄儈僢僞怣崋揹棳偼丄
|
侾侽侽兪俙俹亅俹
|
|
嘔
|
僄儈僢僞懁弌椡抂巕偺弌椡怣崋揹埑倴倧俀偼丄
侾侽侽兪俙俹亅俹亊俈俀兌亖俈丏俀倣倁俹亅俹
|
俈丏俀倣倁俹亅俹
|
俀俀.俋. 楙廗
夞楬偱巊梡偡傞嵟掅偺廃攇悢傪俀侽俫倸偲偟偰丄幷抐廃攇悢傪俆俫倸偵愝掕偟丄壓恾傪嶲峫偵壓昞偵彂偒崬傒側偑傜丄夞楬偵巊梡偝傟偨係偮偺僐儞僨儞僒偺梕検傪寛掕偟偰壓偝偄丅
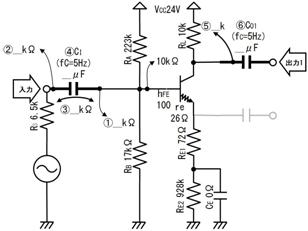
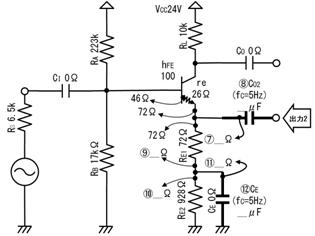
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡僐儞僨儞僒俠俬偺塃懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮俼俙丄俼俛丄儀乕僗偺僀儞僺乕僟儞僗偑暲楍偵尒偊偰丄乯
|
倠兌
|
|
嘇
|
擖椡僐儞僨儞僒俠俬偺嵍懁偐傜怣崋傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘊
|
僐儞僨儞僒偐傜嵍塃傪尒偨僀儞僺乕僟儞僗偼丄乮嘆偲嘇偑捈楍偵尒偊偰丄乯
|
倠兌
|
|
嘋
|
抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄擖椡僐儞僨儞僒俠俬偺梕検偼丄
|
兪俥
|
|
嘍
|
弌椡僐儞僨儞僒俠俷偺嵍懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
弌椡偵愙懕偡傞夞楬偼枹掕偱偡偐傜丄僐儞僨儞僒偺塃懁偵愙懕偝傟傞僀儞僺乕僟儞僗偼侽兌偲峫偊偰丄偙偙偱寁嶼偟偨僀儞僺乕僟儞僗傪丄僐儞僨儞僒偐傜尒偨僀儞僺乕僟儞僗偲峫偊傑偡丅
|
倠兌
|
|
嘐
|
抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄弌椡僐儞僨儞僒俠俷偺梕検偼丄
|
兪俥
|
|
嘑
|
弌椡俀僐儞僨儞僒俠俷俀偺嵍懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮儀乕僗偺僀儞僺乕僟儞僗乮俈俀兌乯偲俼俤侾乮俈俀兌乯偑暲楍偵尒偊偰丄乯
弌椡偵愙懕偡傞夞楬偼枹掕偱偡偐傜丄僐儞僨儞僒偺塃懁偵愙懕偝傟傞僀儞僺乕僟儞僗偼侽兌偲峫偊偰丄偙偙偱寁嶼偟偨僀儞僺乕僟儞僗傪丄僐儞僨儞僒偐傜尒偨僀儞僺乕僟儞僗偲峫偊傑偡丅
|
兌
|
|
嘒
|
抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄弌椡僐儞僨儞僒俠俷俀偺梕検偼丄
|
兪俥
|
|
嘓
|
僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偺忋懁偐傜丄忋傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘔
|
僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偺忋懁偐傜丄壓傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘕
|
僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘖
|
抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偺梕検偼丄
|
兪俥
|
俀俀.侾侽. 摎
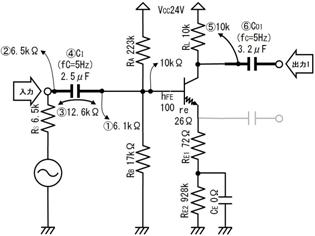
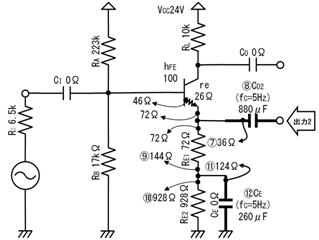
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡僐儞僨儞僒俠俬偺塃懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄=1/(1/10E3+1/223E3+1/17E3)
乮俼俙丄俼俛丄儀乕僗偺僀儞僺乕僟儞僗偑暲楍偵尒偊偰丄乯
|
俇丏侾倠兌
|
|
嘇
|
擖椡僐儞僨儞僒俠俬偺嵍懁偐傜怣崋傪尒偨僀儞僺乕僟儞僗偼丄
|
俇丏俆倠兌
|
|
嘊
|
僐儞僨儞僒偐傜嵍塃傪尒偨僀儞僺乕僟儞僗偼丄乮嘆偲嘇偑捈楍偵尒偊偰丄乯
|
侾俀丏俇倠兌
|
|
嘋
|
抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄擖椡僐儞僨儞僒俠俬偺梕検偼丄=1/2/PI()/5/12.6E3
|
俀丏俆兪俥
|
|
嘍
|
弌椡僐儞僨儞僒俠俷偺嵍懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
|
侾侽倠兌
|
|
嘐
|
抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄弌椡僐儞僨儞僒俠俷偺梕検偼丄=1/2/PI()/5/10E3
弌椡偵愙懕偡傞夞楬偼枹掕偱偡偐傜丄僐儞僨儞僒偺塃懁偵愙懕偝傟傞僀儞僺乕僟儞僗偼侽兌偲峫偊偰丄偙偙偱寁嶼偟偨僀儞僺乕僟儞僗傪丄僐儞僨儞僒偐傜尒偨僀儞僺乕僟儞僗偲峫偊傑偡丅
|
俁丏俀兪俥
|
|
嘑
|
弌椡俀僐儞僨儞僒俠俷俀偺嵍懁偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
乮儀乕僗偺僀儞僺乕僟儞僗乮俈俀兌乯偲俼俤侾乮俈俀兌乯偑暲楍偵尒偊偰丄乯
弌椡偵愙懕偡傞夞楬偼枹掕偱偡偐傜丄僐儞僨儞僒偺塃懁偵愙懕偝傟傞僀儞僺乕僟儞僗偼侽兌偲峫偊偰丄偙偙偱寁嶼偟偨僀儞僺乕僟儞僗傪丄僐儞僨儞僒偐傜尒偨僀儞僺乕僟儞僗偲峫偊傑偡丅
|
俁俇兌
|
|
嘒
|
抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄弌椡僐儞僨儞僒俠俷俀偺梕検偼丄=1/2/PI()/5/36
|
俉俉侽兪俥
|
|
嘓
|
僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偺忋懁偐傜丄忋傪尒偨僀儞僺乕僟儞僗偼丄
|
侾係係兌
|
|
嘔
|
僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偺忋懁偐傜丄壓傪尒偨僀儞僺乕僟儞僗偼丄
|
俋俀俉兌
|
|
嘕
|
僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
|
侾俀係兌
|
|
嘖
|
抐廃攇悢倖俠傪俆俫倸偲偡傟偽丄僄儈僢僞僶僀僷僗僐儞僨儞僒俠俤偺梕検偼丄=1/2/PI()/5/124
|
俀俇侽兪俥
|
壓恾偺傛偆偵丄儀乕僗偵捈棳揹埑偲嫟偵岎棳揹埑傪壛偊傞偲乮倁俛俤偑堦掕偱偡偐傜乯僄儈僢僞偵傕傎傏摨偠岎棳揹埑偑惗偠傑偡丅偲偙傠偑揹棳偼丄椺偊偽僄儈僢僞偵侾倣俙俹亅俹棳傟偰偄偰傕丄儀乕僗偵偼偦偺倛俥俤暘偺侾偺侾侽兪俙俹亅俹偟偐棳傟傑偣傫丅揹埑偑摨偠偱揹棳偑彮側偔側傝傑偡偐傜丄儀乕僗偺岎棳掞峈偼崅偔側傝傑偡丅
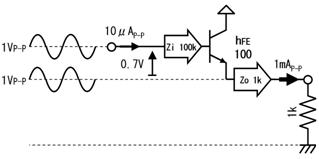
偙傟偑偡偱偵愢柧偟偨乽儀乕僗偺僀儞僺乕僟儞僗偼僄儈僢僞偺僀儞僺乕僟儞僗偺倛俥俤攞偵崅偔側傞乿偲偄偆尰徾偱偡丅偙偺惈幙傪偦偺傑傑憹暆婍偵棙梡偟偨偺偑僄儈僢僞僼僅儘傾偱偡丅乽僼僅儘傾乿偲偼乽偁偲偵偮偄偰乮摨偠傛偆偵乯摦偔乿偲偄偆堄枴偱丄僄儈僢僞偺揹埑偑儀乕僗偺揹埑偲摨偠傛偆偵摦偔偨傔偵柦柤偝傟偰偄傑偡丅
偮傑傝僄儈僢僞僼僅儘傾偼乽揹埑偼憹暆偟側偄乮傎偲傫偳偦偺傑傑弌偰偔傞乯乿偑丄乽揹棳偼倛俥俤攞偵憹暆乿偟丄偦偺寢壥丄乽擖椡僀儞僺乕僟儞僗偼弌椡僀儞僺乕僟儞僗偺倛俥俤攞偵崅偔側傞乿偁傞偄偼乽弌椡僀儞僺乕僟儞僗偼擖椡僀儞僺乕僟儞僗偺倛俥俤暘偺侾偵掅偔側傞乿憹暆婍偱偡丅
壓恾偺椺偱偼丄擖椡偐傜尒傟偽摨恾乮倎乯偺傛偆偵丄怣崋尮偺侾倠兌偺乮崅偄乯僀儞僺乕僟儞僗偑丄弌椡抂巕偐傜偼俁俆兌偲掅偔尒偊偰偄傑偡丅弌椡偐傜尒傟偽摨恾乮倐乯偺傛偆偵丄弌椡偺俀俆兌偺乮掅偄乯僀儞僺乕僟儞僗偑丄擖椡抂巕偐傜偼俆倠兌偲崅偔尒偊偰偄傑偡丅
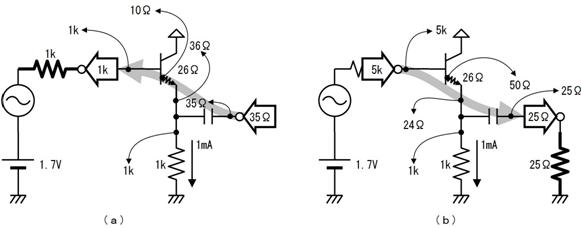
忋恾偺捠傝丄幚嵺偺夞楬偱偼丄倰倕傗僄儈僢僞掞峈偺塭嬁偱丄僀儞僺乕僟儞僗偑傄偭偨傝倛俥俤攞傗倛俥俤暘偺侾偵偼側傝傑偣傫偑丄擖椡僀儞僺乕僟儞僗偼崅偔丄弌椡僀儞僺乕僟儞僗偼掅偔側傝傑偡丅
俀俁.侾. 楙廗
壓恾乮倎乯偺僄儈僢僞僼僅儘傾偺弌椡捈棳揹埑倁俷俷丄弌椡岎棳揹埑倴倧丄弌椡僀儞僺乕僟儞僗倅倧傪壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜媮傔偰偔偩偝偄丅
傑偢丄捈棳専摙偟偰丄倁俷俷傪媮傔傑偡丅
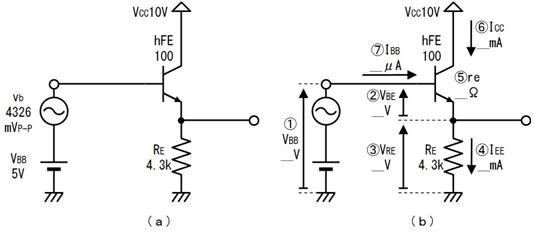
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
儀乕僗僶僀傾僗揹埑倁俛俛偼丄
|
倁
|
|
嘇
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘊
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘋
|
僄儈僢僞僶僀傾僗揹棳俬俤俤偼丄
|
倣俙
|
|
嘍
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕偼丄
俀俇倣倁亐侾倣俙亖俀俇兌
|
兌
|
|
嘐
|
僐儗僋僞僶僀傾僗揹棳俬俠俠偼丄
|
倣俙
|
|
嘑
|
儀乕僗僶僀傾僗揹棳俬俛俛偼丄
|
兪俙
|
俀俁.俀. 摎
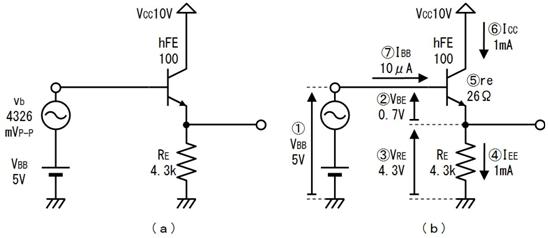
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
儀乕僗僶僀傾僗揹埑倁俛俛偼丄
|
俆倁
|
|
嘇
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘊
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
|
係丏俁倁
|
|
嘋
|
僄儈僢僞僶僀傾僗揹棳俬俤俤偼丄
|
侾倣俙
|
|
嘍
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕偼丄
俀俇倣倁亐侾倣俙亖俀俇兌
|
俀俇兌
|
|
嘐
|
僐儗僋僞僶僀傾僗揹棳俬俠俠偼丄
|
侾倣俙
|
|
嘑
|
儀乕僗僶僀傾僗揹棳俬俛俛偼丄
|
侾侽兪俙
|
俀俁.俁. 楙廗
師偵岎棳専摙偟偰丄弌椡怣崋揹埑倴倧偲丄僀儞僺乕僟儞僗専摙偟偰弌椡僀儞僺乕僟儞僗倅倧傪媮傔傑偡丅
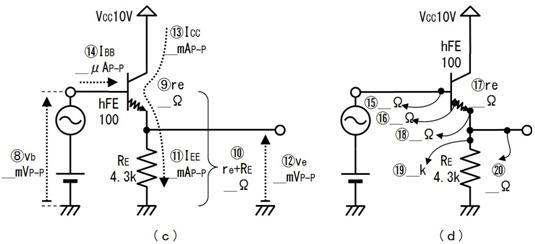
|
斣崋
|
幙栤
|
抣
|
|
嘒
|
儀乕僗怣崋揹埑倴倐倐偼丄
|
倣倁俹亅俹
|
|
嘓
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕偼丄
|
兌
|
|
嘔
|
僄儈僢僞懁偺憤僀儞僺乕僟儞僗偼丄
倰倕亄俼俤亖係俁俀俇兌
|
兌
|
|
嘕
|
僄儈僢僞怣崋揹棳倝倕倕偼丄
|
倣俙俹亅俹
|
|
嘖
|
弌椡怣崋揹埑倴倧乮僄儈僢僞掞峈偺椉抂怣崋揹埑偼丄乯
|
倣倁俹亅俹
|
|
嘗
|
僐儗僋僞怣崋揹棳倝們們偼丄
|
倣俙俹亅俹
|
|
嘙
|
儀乕僗怣崋揹棳倝倐倐偼丄
俬俠俠亐倛俥俤亖侾侽兪俙
|
兪俙俹亅俹
|
|
嘚
|
儀乕僗偐傜嵍傪尒偨僀儞僺乕僟儞僗乮怣崋尮偺僀儞僺乕僟儞僗乯偼丄
|
兌
|
|
嘜
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
侽兌亐倛俥俤亖侽兌
|
兌
|
|
嘝
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕偼丄
|
兌
|
|
嘠
|
僄儈僢僞偺僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘡
|
俼俤偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘢
|
弌椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
俀俇兌乛乛係丏俁倠兌亖俀俇兌
|
兌
|
俀俁.係. 摎
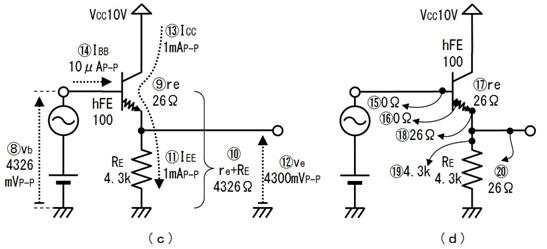
|
斣崋
|
幙栤
|
抣
|
|
嘒
|
儀乕僗怣崋揹埑倴倐倐偼丄
|
係俁俀俆倣倁俹亅俹
|
|
嘓
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕偼丄
|
俀俇兌
|
|
嘔
|
僄儈僢僞懁偺憤僀儞僺乕僟儞僗偼丄
倰倕亄俼俤亖係俁俀俇兌
|
係俁俀俇兌
|
|
嘕
|
僄儈僢僞怣崋揹棳倝倕倕偼丄
|
侾倣俙俹亅俹
|
|
嘖
|
弌椡怣崋揹埑倴倧乮僄儈僢僞掞峈偺椉抂怣崋揹埑偼丄乯
|
係俁侽侽倣倁俹亅俹
|
|
嘗
|
僐儗僋僞怣崋揹棳倝們們偼丄
|
侾倣俙俹亅俹
|
|
嘙
|
儀乕僗怣崋揹棳倝倐倐偼丄
俬俠俠亐倛俥俤亖侾侽兪俙
|
侾侽兪俙俹亅俹
|
|
嘚
|
儀乕僗偐傜嵍傪尒偨僀儞僺乕僟儞僗乮怣崋尮偺僀儞僺乕僟儞僗乯偼丄
|
侽兌
|
|
嘜
|
倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜嵍傪尒偨僀儞僺乕僟儞僗偼丄
侽兌亐倛俥俤亖侽兌
|
侽兌
|
|
嘝
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕偼丄
|
俀俇兌
|
|
嘠
|
僄儈僢僞偺僀儞僺乕僟儞僗偼丄
|
俀俇兌
|
|
嘡
|
俼俤偺忋懁偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
係丏俁倠兌
|
|
嘢
|
弌椡抂巕偐傜夞楬傪尒偨僀儞僺乕僟儞僗偼丄
俀俇兌乛乛係丏俁倠兌亖俀俇兌
|
俀俇兌
|
壓恾偺傛偆偵丄儀乕僗摨巑傪宷偄偩僩儔儞僕僗僞偱偼丄俀偮偺僩儔儞僕僗僞偺倁俛俤偑摨偠偵側傝丄俀偮偺僩儔儞僕僗僞偵偼摨偠戝偒偝偺俬俠偑棳傟傑偡丅傑偨丄僐儗僋僞揹棳偵偼掕揹棳摿惈偑偁傞偨傔丄晧壸掞峈俼俴俀偺抣傪曄峏偟偰傕丄俬俠俀偺抣偼曄壔偟傑偣傫丅
偙偺傛偆偵丄俀偮偺僩儔儞僕僗僞傪慻傒崌傢偣傞偲丄憃曽偺俬俠偑摍偟偔側傝丄晧壸偑曄壔偟偰傕堦掕偺揹棳傪曐偪傑偡丅傑傞偱丄俻侾偺揹棳偑嬀偵塮偭偨傛偆俻俀偵斀塮偝傟傞偨傔丄偙偺夞楬傪乽僇儗儞僩丒儈儔乕乿偲屇傃傑偡丅
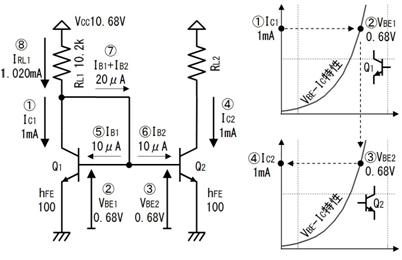
俀係.侾. 妋擣
忋恾傪嶲峫偵壓昞偵彂偒崬傫偱丄夞楬偺摦嶌傪妋擣偟傑偡丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺僐儗僋僞揹棳俬俠侾偼侾倣俙偲偟傑偡丅
|
亅
|
|
嘇
|
倁俛俤亅俬俠摿惈偐傜丄偦偺偲偒偺俻侾偺倁俛俤偼丄
|
倁
|
|
嘊
|
俻侾偲俻俀偺儀乕僗偑宷偑偭偰偄傞偐傜丄俻侾偺倁俛俤偼丄
|
倁
|
|
嘋
|
倁俛俤亅俬俠摿惈偐傜丄偦偺偲偒偺俻侾偺俬俠偼丄
|
倣俙
|
|
嘍
|
倛俥俤偑侾侽侽偩偐傜丄俻侾偺俬俛偼丄
|
兪俙
|
|
嘐
|
摨偠偔俻俀偺俬俛偼丄
|
兪俙
|
|
嘑
|
儀乕僗揹棳偺崌寁偼丄
|
兪俙
|
|
嘒
|
俼俴侾偵棳傟傞揹棳丄俬俼俴侾偼丄
|
倣俙
|
俀係.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺僐儗僋僞揹棳俬俠侾偼侾倣俙偲偟傑偡丅
|
亅
|
|
嘇
|
倁俛俤亅俬俠摿惈偐傜丄偦偺偲偒偺俻侾偺倁俛俤偼丄
|
侽丏俇俉倁
|
|
嘊
|
俻侾偲俻俀偺儀乕僗偑宷偑偭偰偄傞偐傜丄俻侾偺倁俛俤偼丄
|
侽丏俇俉倁
|
|
嘋
|
倁俛俤亅俬俠摿惈偐傜丄偦偺偲偒偺俻侾偺俬俠偼丄
|
侾倣俙
|
|
嘍
|
倛俥俤偑侾侽侽偩偐傜丄俻侾偺俬俛偼丄
|
侾侽兪俙
|
|
嘐
|
摨偠偔俻俀偺俬俛偼丄
|
侾侽兪俙
|
|
嘑
|
儀乕僗揹棳偺崌寁偼丄
|
俀侽兪俙
|
|
嘒
|
俼俴侾偵棳傟傞揹棳丄俬俼俴侾偼丄
|
侾丏侽俀侽倣俙
|
忋昞偱暘偐傞傛偆偵丄俼俴侾偲俼俴俀偵棳傟傞揹棳偵偼丄俀亾掱搙偺嵎偟偐偁傝傑偣傫丅戝嶨攃側愝寁偱偼丄俀偮偺揹棳傪摨偠偲峫偊偰寁嶼偟傑偡丅
倁俛俤偼壏搙曄壔偡傞偨傔丄俻侾偲俻俀偺壏搙偑摨偠偱側偗傟偽丄僐儗僋僞揹棳偑摍偟偔側傝傑偣傫丅偙偺偨傔俀偮偺僩儔儞僕僗僞傪愙拝乮擬寢崌乯偟偰巊梡偟偨傝丄堦偮偺僠僢僾偺忋偵俀偮偺僩儔儞僕僗僞傪嶌傝偙傫偩乽僨儏傾儖僩儔儞僕僗僞乿傪巊梡偟傑偡丅
僆儁傾儞僾俬俠偱偼慡偰偺僩儔儞僕僗僞偑堦偮偺僠僢僾偺忋偵嶌傝崬傑傟偰偄傑偡偐傜丄僨儏傾儖僩儔儞僕僗僞摨條偵僇儗儞僩儈儔乕偼惛搙椙偔摦嶌偟傑偡丅偨偩偟丄擬傪敪偡傞弌椡僩儔儞僕僗僞傑偱摨偠僠僢僾偵嶌傝崬傑傟偰偄傞偨傔丄偦偺塭嬁傪庴偗傞偺偑擸傒偺庬偱偡丅偦偙偱丄僠僢僾忋偺攝抲傪岺晇偟偰丄偨偲偊弌椡夞楬偑敪擬偟偰傕丄俀偮偺僩儔儞僕僗僞偺壏搙偑摨偠偵側傞傛偆偵攝椂偝傟偰偄傑偡丅
俀係.俁. 楙廗
壓恾偺夞楬偺俻俀偺僐儗僋僞揹棳俬俠俀傪壓昞偵彂偒崬傒側偑傜媮傔偰偔偩偝偄丅
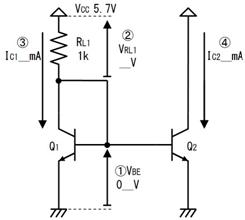
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘇
|
倁俠俠偑俆丏俈倁側偺偱丄俼俴侾偺椉抂揹埑偼丄
|
倁
|
|
嘊
|
俻侾偺僐儗僋僞揹棳俬俠侾偼丄
|
倣俙
|
|
嘋
|
俻俀偺僐儗僋僞揹棳俬俠俀偼丄
|
倣俙
|
俀係.係. 摎
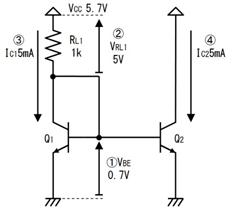
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘇
|
倁俠俠偑俆丏俈倁側偺偱丄俼俴侾偺椉抂揹埑偼丄
|
俆倁
|
|
嘊
|
俻侾偺僐儗僋僞揹棳俬俠侾偼丄
|
俆倣俙
|
|
嘋
|
俻俀偺僐儗僋僞揹棳俬俠俀偼丄
|
俆倣俙
|
俀係.俆. 楙廗
壓恾偺傛偆偵僄儈僢僞掞峈傪憓擖偡傞偙偲偵傛偭偰丄嵍塃偱堎側傞揹棳傪棳偡偙偲傕偱偒傑偡丅
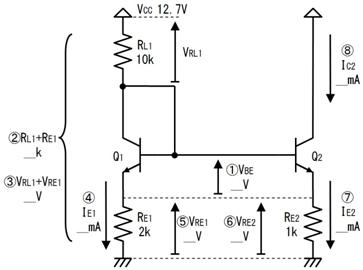
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘇
|
俻侾偺僐儗僋僞掞峈俼俴侾偲僄儈僢僞掞峈俼俤侾偺崌寁抣偼丄
|
倠兌
|
|
嘊
|
俼俴侾偺椉抂揹埑倁俼俴侾偲丄俼俤侾偺椉抂揹埑倁俼俤侾偺崌寁揹埑偼丄
|
倁
|
|
嘋
|
俼俴侾偲俼俤侾偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘍
|
俻侾偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
|
倁
|
|
嘐
|
俻俀偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤俀偼丄
|
倁
|
|
嘑
|
俻俀偺僄儈僢僞揹棳俬俤俀偼丄
|
倣俙
|
|
嘒
|
俻俀偺僐儗僋僞揹棳俬俠俀偼丄
|
倣俙
|
俀係.俇. 摎
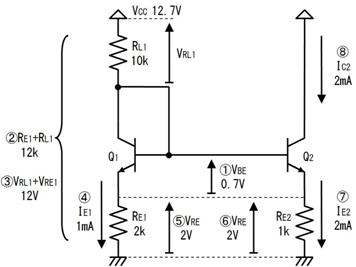
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘇
|
俻侾偺僐儗僋僞掞峈俼俴侾偲僄儈僢僞掞峈俼俤侾偺崌寁抣偼丄
|
侾俀倠兌
|
|
嘊
|
俼俴侾偺椉抂揹埑倁俼俴侾偲丄俼俤侾偺椉抂揹埑倁俼俤侾偺崌寁揹埑偼丄
|
侾俀倁
|
|
嘋
|
俼俴侾偲俼俤侾偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘍
|
俻侾偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
|
俀倁
|
|
嘐
|
俻俀偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤俀偼丄
|
俀倁
|
|
嘑
|
俻俀偺僄儈僢僞揹棳俬俤俀偼丄
|
俀倣俙
|
|
嘒
|
俻俀偺僐儗僋僞揹棳俬俠俀偼丄
|
俀倣俙
|
僄儈僢僞掞峈偼丄嵍塃偺僩儔儞僕僗僞偺揹棳傪曄偊傞偩偗偱偼側偔丄僄儈僢僞掞峈偺偁傞憹暆婍偲摨條偵丄倁俛俤偺壏搙曄壔傗倛俥俤偺偽傜偮偒傪娚榓偡傞岠壥偑偁傝傑偡丅偮傑傝丄嵍塃偺揹棳偑摨偠応崌偱傕丄僄儈僢僞掞峈偵傛偭偰埨掕搙偑岦忋偟傑偡丅
憹暆婍偺憹暆棪傪崅偔偡傞曽朄傪峫偊傑偡丅壓恾乮倎乯偺憹暆婍偱偼丄憹暆棪偼僄儈僢僞掞峈俼俤偲晧壸掞峈俼俴偺斾棪偱寛傑傝傑偡丅偮傑傝丄俼俴偑戝偒偄掱憹暆棪傪崅偔偱偒傑偡丅偙偺夞楬偱偼丄俼俴偑丄俀倠兌丄係倠兌丄俇倠兌偲戝偒偔側傟偽丄憹暆棪偼俀攞丄係攞丄俇攞偲戝偒偔側傝傑偡丅
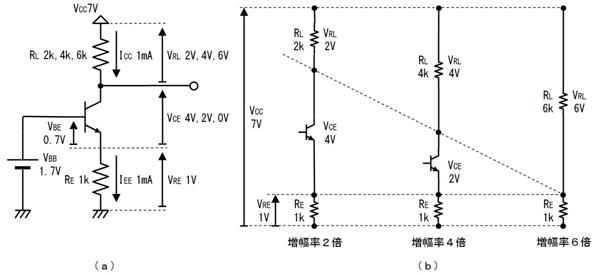
偟偐偟丄忋恾乮倐乯偱暘偐傞傛偆偵丄俼俴偑戝偒偔側傞偵偮傟倁俼俴傕戝偒偔側傝丄媡偵倁俠俤偼彫偝偔側傝傑偡丅偦偟偰偮偄偵丄俼俴偑俇倠兌偵側傞偲倁俠俤偑侽倁偵側偭偰夞楬偼摦嶌偟側偔側傝傑偡丅偮傑傝丄扨偵俼俴傪戝偒偔偡傞曽朄偱偼丄憹暆棪偑廫暘戝偒偔側傞慜偵夞楬偑摦嶌偟側偔側偭偰偟傑偄傑偡丅
偲偙傠偱倁俼俴偑敪惗偡傞尨場偼丄俼俴偵僐儗僋僞僶僀傾僗揹棳俬俠俠偑棳傟偰偄傞偨傔偱偡丅傕偟丄俼俴偵棳傟傞揹棳傪尭傜偡偙偲偑偱偒傟偽丄俼俴傪傕偭偲戝偒偔偱偒傑偡丅
偟偐偟丄俬俠俠偼夞楬偺摦嶌偵昁梫側揹棳偱偡偐傜尭傜偡偙偲偼偱偒傑偣傫丅偦偙偱壓恾偺傛偆偵丄俬俠俠傪丄俼俴偲偼暿偺宱楬偱嫙媼偟偰丄俼俴偵棳傟傞揹棳傪尭傜偡曽朄偑岺晇偝傟傑偟偨丅偙傟偑傾僋僥傿僽儘乕僪乮擻摦晧壸乯偱偡丅
乽擻摦乮傾僋僥傿僽乯乿偲偼僩儔儞僕僗僞偺傛偆側乽憹暆嶌梡乿偺帠偱丄乮憹暆嶌梡偺柍偄乯掞峈偺戙傝偵丄僩儔儞僕僗僞乮擻摦慺巕乯傪乽晧壸乮儘乕僪乯乿偵巊偆偺偱丄乽擻摦晧壸乿偲屇偽傟傑偡丅
壓恾偺夞楬偱偼丄僇儗儞僩儈儔乕夞楬傪巊梡偟偰丄俼俴偲偼暿宱楬偱侽丏俋倣俙偺揹棳傪僐儗僋僞偵嫙媼偟偰偄傑偡丅偙偺偨傔丄俼俴傪棳傟傞揹棳偼侽丏侾倣俙偲彫偝偔側傝丄俼俴傪俁侽倠兌偲崅偔偟丄俁侽攞偺憹暆棪傪摼傞偙偲偑偱偒傑偡丅
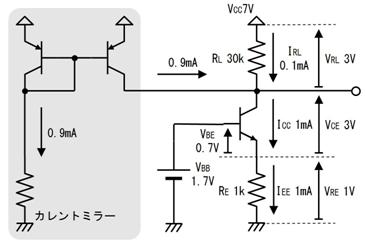
俀俆.侾. 妋擣
壓恾偺夞楬偺怣崋憹暆棪傪壓昞偵婰擖偟側偑傜妋擣偟偰偔偩偝偄丅
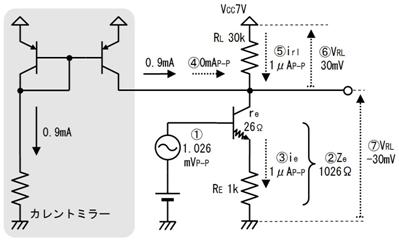
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
儀乕僗偵壛傢傞怣崋揹埑倴倐偼丄
|
倣倁俹亅俹
|
|
嘇
|
僄儈僢僞懁偺崌寁僀儞僺乕僟儞僗倅倕偼丄
|
兌
|
|
嘊
|
僄儈僢僞怣崋揹棳倝倕偼丄
|
兪俙俹亅俹
|
|
嘋
|
僇儗儞僩儈儔乕偐傜棳傟崬傓怣崋揹棳偼丄
乮僇儗儞僩儈儔乕偺弌椡偼丄掕揹棳偱偁傞丅掕揹棳偲偼乽揹棳慡偔曄摦偟側偄乿偲偄偆帠偩偐傜丄曄摦偡傞揹棳偱偁傞怣崋揹棳偼丄乯
|
倣俙俹亅俹
|
|
嘍
|
晧壸掞峈俼俴偵棳傟傞怣崋揹棳倝倰倢偼丄
|
兪俙俹亅俹
|
|
嘐
|
晧壸掞峈偺椉抂偵尰傟傞怣崋揹埑倴倰倢偼丄
|
倣倁俹亅俹
|
|
嘑
|
弌椡抂巕偵尰傟傞怣崋揹埑倴倧偼丄
|
倣倁俹亅俹
|
|
嘒
|
揹埑憹暆棪偼丄
|
攞
|
俀俆.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
儀乕僗偵壛傢傞怣崋揹埑倴倐偼丄
|
侾丏侽俀俇倣倁俹亅俹
|
|
嘇
|
僄儈僢僞懁偺崌寁僀儞僺乕僟儞僗倅倕偼丄
|
侾侽俀俇兌
|
|
嘊
|
僄儈僢僞怣崋揹棳倝倕偼丄
|
侾兪俙俹亅俹
|
|
嘋
|
僇儗儞僩儈儔乕偐傜棳傟崬傓怣崋揹棳偼丄
乮僇儗儞僩儈儔乕偺弌椡偼丄掕揹棳偱偁傞丅掕揹棳偲偼乽揹棳慡偔曄摦偟側偄乿偲偄偆帠偩偐傜丄曄摦偡傞揹棳偱偁傞怣崋揹棳偼丄乯
|
侽倣俙俹亅俹
|
|
嘍
|
晧壸掞峈俼俴偵棳傟傞怣崋揹棳倝倰倢偼丄
|
侾兪俙俹亅俹
|
|
嘐
|
晧壸掞峈偺椉抂偵尰傟傞怣崋揹埑倴倰倢偼丄
|
俁侽倣倁俹亅俹
|
|
嘑
|
弌椡抂巕偵尰傟傞怣崋揹埑倴倧偼丄
|
亅俁侽倣倁俹亅俹
|
|
嘒
|
揹埑憹暆棪偼丄
|
亅俁侽攞
|
憹暆棪偼丄僄儈僢僞僶僀僷僗僐儞僨儞僒傪庢傝晅偗偰崅傔傞偙偲傕偱偒傑偡偑丄捈棳偵偼乮僐儞僨儞僒偼捈棳傪捠偝側偄偨傔乯岠壥偑偁傝傑偣傫丅偙傟偲偼堘偄丄傾僋僥傿僽儘乕僪偼捈棳偺憹暆棪傕崅傔傞偙偲偑偱偒傑偡丅
俀俆.俁. 楙廗
壓恾偺夞楬傪捈棳専摙偟偰徚旓揹棳傪媮傔丄岎棳専摙偟偰憹暆棪傪媮傔偰偔偩偝偄丅
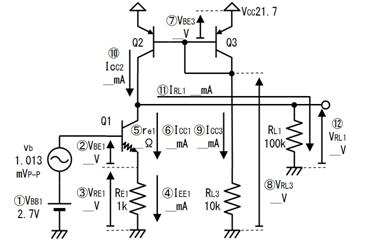
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺儀乕僗僶僀傾僗揹埑倁俛俛侾偼丄
|
俀丏俈倁
|
|
嘇
|
俻侾偺儀乕僗僄儈僢僞娫揹埑倁俛俤侾偼丄
|
倁
|
|
嘊
|
俻侾偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
|
倁
|
|
嘋
|
俻侾偺僄儈僢僞僶僀傾僗揹棳俬俤俤侾偼丄
|
倣俙
|
|
嘍
|
俻侾偺僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕侾偼丄
|
兌
|
|
嘐
|
俻侾偺僐儗僋僞僶僀傾僗揹棳侾俠俠侾偼丄
|
倣俙
|
|
嘑
|
俻俁偺儀乕僗僄儈僢僞娫揹埑倁俛俤侾偼丄
|
倁
|
|
嘒
|
俻俁偺晧壸掞峈俼俴俁偺椉抂揹埑倁俼俴俁偼丄
|
倁
|
|
嘓
|
俻俁偺僐儗僋僞揹棳俬俠俠俁偼丄
|
倣俙
|
|
嘔
|
俻俀偺僐儗僋僞揹棳俬俠俠俀偼丄
乮俻俀偲俻俁偼僇儗儞僩儈儔乕偩偐傜丄乯
|
倣俙
|
|
嘕
|
晧壸掞峈俼俴侾偵棳傟傞揹棳俬俼俴侾偼丄
|
倣俙
|
|
嘖
|
晧壸掞峈俼俴侾偺椉抂揹埑倁俼俴侾偼丄
|
倁
|
俀俆.係. 摎
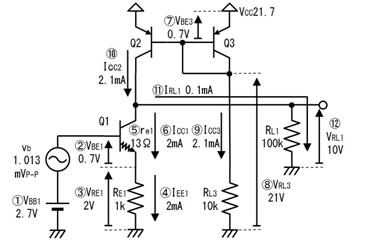
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺儀乕僗僶僀傾僗揹埑倁俛俛侾偼丄
|
俀丏俈倁
|
|
嘇
|
俻侾偺儀乕僗僄儈僢僞娫揹埑倁俛俤侾偼丄
|
侽丏俈倁
|
|
嘊
|
俻侾偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
|
俀倁
|
|
嘋
|
俻侾偺僄儈僢僞僶僀傾僗揹棳俬俤俤侾偼丄
|
俀倣俙
|
|
嘍
|
俻侾偺僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕侾偼丄
|
侾俁兌
|
|
嘐
|
俻侾偺僐儗僋僞僶僀傾僗揹棳侾俠俠侾偼丄
|
俀倣俙
|
|
嘑
|
俻俁偺儀乕僗僄儈僢僞娫揹埑倁俛俤侾偼丄
|
侽丏俈倁
|
|
嘒
|
俻俁偺晧壸掞峈俼俴俁偺椉抂揹埑倁俼俴俁偼丄
|
俀侾倁
|
|
嘓
|
俻俁偺僐儗僋僞揹棳俬俠俠俁偼丄
|
俀丏侾倣俙
|
|
嘔
|
俻俀偺僐儗僋僞揹棳俬俠俠俀偼丄
乮俻俀偲俻俁偼僇儗儞僩儈儔乕偩偐傜丄乯
|
俀丏侾倣俙
|
|
嘕
|
晧壸掞峈俼俴侾偵棳傟傞揹棳俬俼俴侾偼丄
|
侽丏侾倣俙
|
|
嘖
|
晧壸掞峈俼俴侾偺椉抂揹埑倁俼俴侾偼丄
|
侾侽倁
|
俀俆.俆. 楙廗
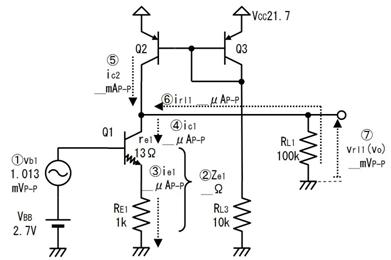
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺儀乕僗偵壛傢傞怣崋揹埑倴倐侾偼丄
|
侾丏侽俁侾倣倁俹亅俹
|
|
嘇
|
俻侾偺僄儈僢僞懁僀儞僺乕僟儞僗偺崌寁倅倕侾偼丄
|
兌
|
|
嘊
|
俻侾偺僄儈僢僞怣崋揹棳倝倕侾偼丄
|
兪俙俹亅俹
|
|
嘋
|
俻侾偺僐儗僋僞怣崋揹棳倝們侾偼丄
|
兪俙俹亅俹
|
|
嘍
|
俻俀偺僐儗僋僞怣崋揹棳倝們俀偼丄
乮俻俀偲俻俁偼僇儗儞僩儈儔乕偱丄俻俀偺僐儗僋僞揹棳偼掕揹棳偩偐傜丄乯
|
倣俙俹亅俹
|
|
嘐
|
晧壸掞峈俼俴侾偵棳傟傞怣崋揹棳倝倰倢侾偼丄
|
兪俙俹亅俹
|
|
嘑
|
晧壸掞峈俼俴侾偺椉抂揹埑倴倰倢侾偼丄
|
倣倁俹亅俹
|
|
嘒
|
偙偺夞楬偺揹埑憹暆棪偼丄
|
栺丂丂丂攞
|
俀俆.俇. 摎
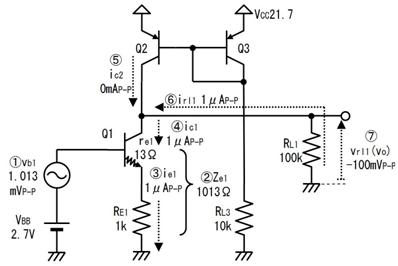
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺儀乕僗偵壛傢傞怣崋揹埑倴倐侾偼丄
|
侾丏侽俁侾倣倁俹亅俹
|
|
嘇
|
俻侾偺僄儈僢僞懁僀儞僺乕僟儞僗偺崌寁倅倕侾偼丄
|
侾侽侾俁兌
|
|
嘊
|
俻侾偺僄儈僢僞怣崋揹棳倝倕侾偼丄
|
侾兪俙俹亅俹
|
|
嘋
|
俻侾偺僐儗僋僞怣崋揹棳倝們侾偼丄
|
侾兪俙俹亅俹
|
|
嘍
|
俻俀偺僐儗僋僞怣崋揹棳倝們俀偼丄
乮俻俀偲俻俁偼僇儗儞僩儈儔乕偱丄俻俀偺僐儗僋僞揹棳偼掕揹棳偩偐傜丄乯
|
侽倣俙俹亅俹
|
|
嘐
|
晧壸掞峈俼俴侾偵棳傟傞怣崋揹棳倝倰倢侾偼丄
|
侾兪俙俹亅俹
|
|
嘑
|
晧壸掞峈俼俴侾偺椉抂揹埑倴倰倢侾偼丄
|
乕侾侽侽倣倁俹亅俹
|
|
嘒
|
偙偺夞楬偺揹埑憹暆棪偼丄
|
栺俋俋攞
|
壓恾乮倎乯偼扨弮側憹暆婍偱偡丅僩儔儞僕僗僞傪摦嶌偝偣傞偨傔偵偼丄怣崋偲捈楍偵侽丏俈倁偺揹埑傪壛偊傞昁梫偑偁傝傑偟偨丅偟偐偟丄擖椡偵捈棳傪壛偊傞偺偼柺搢偱偡偐傜丄偱偒傟偽怣崋傪捈愙儀乕僗偵愙懕偟偨偄偲偙傠偱偡丅
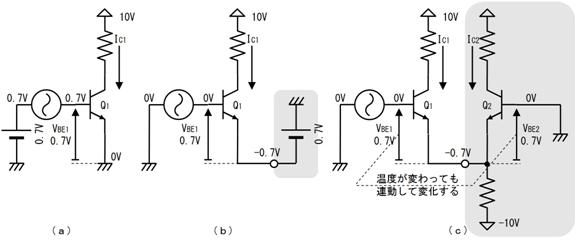
偦偙偱忋恾乮倐乯偺傛偆偵丄儀乕僗偺揹埑傪忋偘傞偺偱偼側偔丄僄儈僢僞偺揹埑傪壓偘傞偙偲偱丄儀乕僗偵捈愙怣崋傪壛偊傞偙偲偑偱偒傑偡丅
偨偩偟丄偙偺曽朄偵偼寚揰偑偁傝傑偡丅偮傑傝乽倁俛俤偼侽丏俈倁掱搙偱傎傏堦掕乿偲偼尵偆傕偺偺丄壏搙偱曄壔乮侾亷偁偨傝栺俀倣倁掅壓乯偡傞偨傔丄壏搙曄壔偵崌傢偣偰揹抮偺揹埑傪挷愡偟側偄偲丄俬俠傪堦掕偵曐偮偙偲偑偱偒傑偣傫丅
偦偙偱丄忋恾乮們乯偺傛偆偵丄傕偆堦偮偺乮摨堦昳庬偺乯僩儔儞僕僗僞乮俻俀乯傪梡堄偟丄儀乕僗傪傾乕僗偵愙懕偟丄僄儈僢僞掞峈傪晧揹尮偵愙懕偡傟偽丄俻俀偺僄儈僢僞偺揹埑偼亅侽丏俈倁偲側傝傑偡丅偙偺亅侽丏俈倁傪丄揹抮偺戙傢傝偵棙梡偡傞偙偲偱丄乮俻侾偺倁俛俤侾偲俻俀偺倁俛俤俀偼丄壏搙偵懳偟偰摨偠曄壔傪偟傑偡偐傜乯俬俠偼壏搙偵塭嬁偝傟側偔側傝傑偡丅
忋恾乮們乯偺夞楬偵丄弌椡抂巕傪捛壛偟偰僶儔儞僗傛偔彂偒捈偟偨夞楬傪壓恾乮倎乯偵帵偟傑偡丅偙偺傛偆偵俀偮偺憹暆婍傪僄儈僢僞偱偮側偄偩夞楬傪乽嵎摦憹暆夞楬乿偲屇傃傑偡丅儀乕僗傪侽倁偵愙懕偱偒傞傛偆偵丄僄儈僢僞偼晧偺揹埑偵曐偪傑偡丅偦偺偨傔丄惓揹尮倁俠俠偩偗偱側偔丄晧揹尮倁俤俤偑昁梫偱偡丅
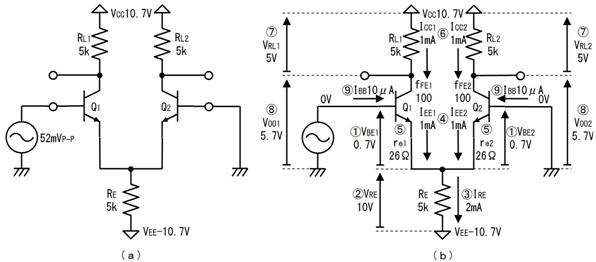
俀俇.侾. 妋擣
忋恾乮倎乯傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜丄嵎摦憹暆夞楬傪捈棳専摙偟丄俀偮偺弌椡抂巕偺揹埑倁俷俷侾偲倁俷俷俀傪媮傔偰壓偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘇
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘊
|
僄儈僢僞掞峈偵棳傟傞揹棳俬俼俤偼丄
|
倣俙
|
|
嘋
|
夞楬偺嵍塃偼摨偠宍乮懳徧乯偩偐傜丄僄儈僢僞僶僀傾僗揹棳俬俤俤侾偲俬俤俤俀偼丄偄偢傟傕丄
|
倣俙
|
|
嘍
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕侾偲倰倕俀偼丄
|
兌
|
|
嘐
|
僐儗僋僞僶僀傾僗揹棳俬俠俠侾偲俬俠俠俀偼丄偄偢傟傕丄
|
倣俙
|
|
嘑
|
晧壸掞峈俼俴侾偲俼俴俀偺椉抂揹埑倁俼俴侾偲倁俼俴俀偼丄
|
倁
|
|
嘒
|
弌椡抂巕偺捈棳揹埑倁俷俷侾偲倁俷俷俀偼丄
|
倁
|
|
嘓
|
儀乕僗僶僀傾僗揹棳俬俛俛侾偲俬俛俛俀偼丄
|
兪俙
|
俀俇.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘇
|
僄儈僢僞掞峈俼俤偺椉抂揹埑倁俼俤偼丄
|
侾侽倁
|
|
嘊
|
僄儈僢僞掞峈偵棳傟傞揹棳俬俼俤偼丄
|
俀倣俙
|
|
嘋
|
夞楬偺嵍塃偼摨偠宍乮懳徧乯偩偐傜丄僄儈僢僞僶僀傾僗揹棳俬俤俤侾偲俬俤俤俀偼丄偄偢傟傕丄
|
侾倣俙
|
|
嘍
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕侾偲倰倕俀偼丄
|
俀俇兌
|
|
嘐
|
僐儗僋僞僶僀傾僗揹棳俬俠俠侾偲俬俠俠俀偼丄偄偢傟傕丄
|
侾倣俙
|
|
嘑
|
晧壸掞峈俼俴侾偲俼俴俀偺椉抂揹埑倁俼俴侾偲倁俼俴俀偼丄
|
俆倁
|
|
嘒
|
弌椡抂巕偺捈棳揹埑倁俷俷侾偲倁俷俷俀偼丄
|
俆丏俈倁
|
|
嘓
|
儀乕僗僶僀傾僗揹棳俬俛俛侾偲俬俛俛俀偼丄
|
侾侽兪俙
|
俀俇.俁. 妋擣
壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜丄嵎摦憹暆夞楬傪僀儞僺乕僟儞僗媦傃岎棳専摙偟丄俀偮偺弌椡抂巕偺怣崋揹埑倴倧侾偲倴倧俀傪妋擣偟偰偔偩偝偄丅
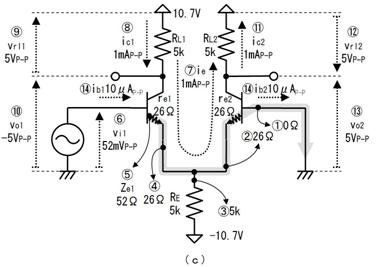
|
斣崋
|
幙栤
|
抣
|
|
|
傑偢丄俻侾偺僄儈僢僞偺僀儞僺乕僟儞僗傪専摙偟傑偡丅
|
亅
|
|
嘆
|
俻俀偺儀乕僗偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘇
|
俻俀偺僄儈僢僞偐傜儀乕僗乮忋乯傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘊
|
俼俤偺忋懁偐傜儅僀僫僗揹尮倁俤俤傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘋
|
俻侾偺僄儈僢僞偐傜壓傪尒偨僀儞僺乕僟儞僗偼丄
乮嘇偲嘊偑暲楍偵尒偊偰丄乯
|
兌
|
|
嘍
|
俻侾偺倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜塃傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
|
師偵岎棳専摙傪偟傑偡丅
|
亅
|
|
嘐
|
儀乕僗偵壛傢傞怣崋揹埑倴倝侾偼丄
|
倣倁俹亅俹
|
|
嘑
|
僄儈僢僞怣崋揹棳倝倕偼丄
乮嘍偲嘐偐傜丄乯
|
倣俙俹亅俹
|
|
嘒
|
俻侾偺僐儗僋僞怣崋揹棳倝們侾偼丄
|
倣俙俹亅俹
|
|
嘓
|
俻侾偺晧壸掞峈俼俴侾偺椉抂怣崋揹埑倴倰倢侾偼丄
|
倁俹亅俹
|
|
嘔
|
弌椡抂巕偺怣崋揹埑倴倧侾偼丄
|
倁俹亅俹
|
|
嘕
|
俻俀偺僐儗僋僞怣崋揹棳倝們俀偼丄
|
倣俙俹亅俹
|
|
嘖
|
俻侾偺晧壸掞峈俼俴俀偺椉抂怣崋揹埑倴倰倢俀偼丄
乮扐偟丄揹埑偺栴報偼壓岦偒偱偡乯
|
倁俹亅俹
|
|
嘗
|
弌椡抂巕偺怣崋揹埑倴倧俀偼丄
乮栴報偺岦偒偵拲堄偟偰丄乯
|
倁俹亅俹
|
|
嘙
|
儀乕僗怣崋揹棳倝倐侾丄倝倐俀偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
兪俙俹亅俹
|
俀俇.係. 摎
|
斣崋
|
幙栤
|
抣
|
|
|
傑偢丄俻侾偺僄儈僢僞偺僀儞僺乕僟儞僗傪専摙偟傑偡丅
|
亅
|
|
嘆
|
俻俀偺儀乕僗偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘇
|
俻俀偺僄儈僢僞偐傜儀乕僗乮忋乯傪尒偨僀儞僺乕僟儞僗偼丄
|
俀俇兌
|
|
嘊
|
俼俤偺忋懁偐傜儅僀僫僗揹尮倁俤俤傪尒偨僀儞僺乕僟儞僗偼丄
|
俆倠兌
|
|
嘋
|
俻侾偺僄儈僢僞偐傜壓傪尒偨僀儞僺乕僟儞僗偼丄
乮嘇偲嘊偑暲楍偵尒偊偰丄乯
|
俀俇兌
|
|
嘍
|
俻侾偺倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜塃傪尒偨僀儞僺乕僟儞僗偼丄
|
俆俀兌
|
|
|
師偵岎棳専摙傪偟傑偡丅
|
亅
|
|
嘐
|
儀乕僗偵壛傢傞怣崋揹埑倴倝侾偼丄
|
俆俀倣倁俹亅俹
|
|
嘑
|
僄儈僢僞怣崋揹棳倝倕偼丄
乮嘍偲嘐偐傜丄乯
|
侾倣俙俹亅俹
|
|
嘒
|
俻侾偺僐儗僋僞怣崋揹棳倝們侾偼丄
|
侾倣俙俹亅俹
|
|
嘓
|
俻侾偺晧壸掞峈俼俴侾偺椉抂怣崋揹埑倴倰倢侾偼丄
|
俆倁俹亅俹
|
|
嘔
|
弌椡抂巕偺怣崋揹埑倴倧侾偼丄
|
亅俆倁俹亅俹
|
|
嘕
|
俻俀偺僐儗僋僞怣崋揹棳倝們俀偼丄
|
侾倣俙俹亅俹
|
|
嘖
|
俻俀偺晧壸掞峈俼俴俀偺椉抂怣崋揹埑倴倰倢俀偼丄
乮扐偟丄揹埑偺栴報偼壓岦偒偱偡乯
|
俆倁俹亅俹
|
|
嘗
|
弌椡抂巕偺怣崋揹埑倴倧俀偼丄
乮栴報偺岦偒偵拲堄偟偰丄乯
|
俆倁俹亅俹
|
|
嘙
|
儀乕僗怣崋揹棳倝倐侾丄倝倐俀偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
侾侽兪俙俹亅俹
|
偙偺傛偆偵丄俻侾偺儀乕僗偵怣崋傪壛偊傞偩偗偱丄俻侾偲俻俀椉曽偺僄儈僢僞偵怣崋揹棳偑棳傟丄椉曽偺弌椡抂巕偵怣崋偑弌椡偝傟傑偡丅
嵎摦憹暆夞楬偱偼丄壓恾偵奃怓栴報偱帵偡傛偆偵怣崋揹棳偑棳傟傑偡丅嵍懁偐傜俻侾偺儀乕僗偵棳傟崬傫偩怣崋揹棳偼丄倛俥俤攞偵憹暆偝傟偰丄俻侾偺僄儈僢僞怣崋揹棳偵側傝丄俻俀偵岦偐偭偰塃岦偒偺丄偦偟偰忋岦偒偵搊偭偰備偒傑偡丅偙偺傛偆偵偟偰棳傟偨俻俀偺僄儈僢僞揹棳偺倛俥俤暘偺侾偑丄俻俀偺儀乕僗怣崋揹棳偲側傝丄塃傊棳傟弌偰備偒傑偡丅
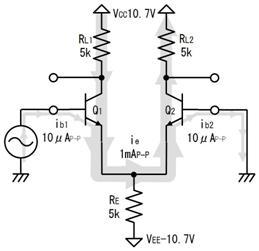
儀乕僗怣崋揹棳偵拲栚偡傞偲丄忋恾偵奃怓嵶栴報偱帵偡傛偆偵丄俻侾偺儀乕僗偐傜擖偭偰僄儈僢僞傪捠傝丄俻俀偺儀乕僗偐傜棳傟弌偟傑偡丅傑偨丄僐儗僋僞傗僄儈僢僞怣崋揹棳偼丄忋恾偵奃怓懢栴報偱帵偡傛偆偵丄倀帤宆偵棳傟傑偡丅
壓恾偵丄嵎摦憹暆夞楬偵怣崋揹棳偑棳傟傞僀儊乕僕傪帵偟傑偡丅
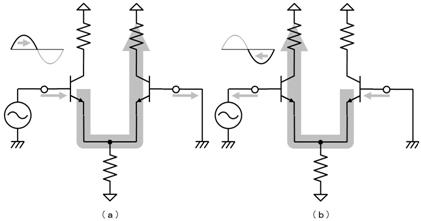
怣崋揹棳偼乽惓乿乽晧乿傪孞傝曉偡岎棳偱偡偐傜丄夞楬偼忋恾乮倎乯偺忬懺偲丄忋恾乮倐乯偺忬懺傪岎屳偵孞傝曉偟偰丄夞楬撪偵偼揹棳偑峴偒棃偟傑偡丅
偙偺恾偱暘偐傞傛偆偵丄嵍塃偺僩儔儞僕僗僞偺僄儈僢僞傗僐儗僋僞偵偼摨偠揹棳偑棳傟傑偡偐傜丄弌椡抂巕傪偳偪傜偺僩儔儞僕僗僞偵愝偗偰傕丄摨偠揹埑偺乮埵憡偼媡乯偺弌椡偑摼傜傟傑偡丅
俀俇.俆. 楙廗
壓恾偺嵎摦憹暆夞楬傪捈棳専摙偟丄弌椡捈棳揹埑倁俷俷傪媮傔丄僀儞僺乕僟儞僗専摙丄岎棳専摙偟偰丄怣崋弌椡揹埑倴倧傪媮傔偰偔偩偝偄丅
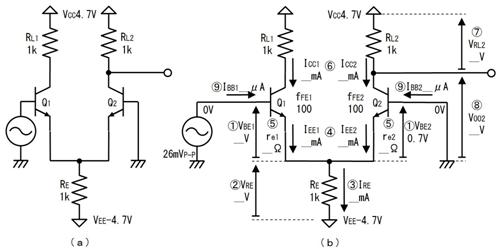
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
|
|
嘆
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘇
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘊
|
僄儈僢僞掞峈偺揹棳俬俼俤偼丄
|
倣俙
|
|
嘋
|
俻侾偲俻俀偺僄儈僢僞僶僀傾僗揹棳丄俬俤俤侾偲俬俤俤俀偼丄
|
倣俙
|
|
嘍
|
俻侾偲俻俀偺僄儈僢僞摍壙僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘐
|
俻侾偲俻俀偺僐儗僋僞僶僀傾僗揹棳丄俬俠俠侾偲俬俠俠俀偼丄
|
倣俙
|
|
嘑
|
俻俀偺晅壛掞峈偺椉抂揹埑倁俼俴俀偼丄
|
倁
|
|
嘒
|
弌椡捈棳乮僶僀傾僗乯揹埑倁俷俷偼丄
|
倁
|
俀俇.俇. 摎
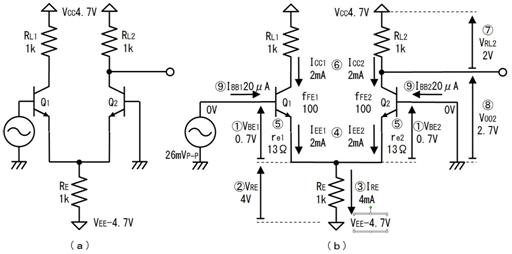
|
斣崋
|
幙栤
|
抣
|
|
|
捈棳偵偮偄偰峫偊傑偡丅
|
|
|
嘆
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘇
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
|
係倁
|
|
嘊
|
僄儈僢僞掞峈偺揹棳俬俼俤偼丄
|
係倣俙
|
|
嘋
|
俻侾偲俻俀偺僄儈僢僞僶僀傾僗揹棳丄俬俤俤侾偲俬俤俤俀偼丄
|
俀倣俙
|
|
嘍
|
俻侾偲俻俀偺僄儈僢僞摍壙僀儞僺乕僟儞僗偼丄
|
侾俁兌
|
|
嘐
|
俻侾偲俻俀偺僐儗僋僞僶僀傾僗揹棳丄俬俠俠侾偲俬俠俠俀偼丄
|
俀倣俙
|
|
嘑
|
俻俀偺晅壛掞峈偺椉抂揹埑倁俼俴俀偼丄
|
俀倁
|
|
嘒
|
弌椡捈棳乮僶僀傾僗乯揹埑倁俷俷偼丄
|
俀丏俈倁
|
俀俇.俈. 楙廗
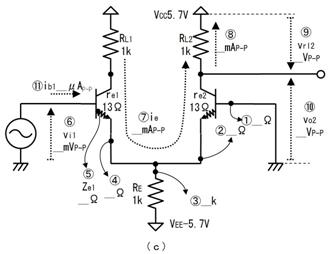
|
斣崋
|
幙栤
|
抣
|
|
|
俻侾偺僄儈僢僞僀儞僺乕僟儞僗傪専摙偟傑偡丅
|
|
|
嘆
|
俻俀偺儀乕僗偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘇
|
俻俀偺僄儈僢僞偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘊
|
僄儈僢僞掞峈俼俤偐傜儅僀僫僗揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘋
|
俻侾偺僄儈僢僞偐傜塃懁傪尒偨僀儞僺乕僟儞僗偼丄
乮嘇偲嘊偑暲楍偵尒偊偰乯
|
兌
|
|
嘍
|
俻侾偺倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜塃傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
|
夞楬傪岎棳専摙偟傑偡丅
|
|
|
嘐
|
俻侾偺儀乕僗偵壛傢傞怣崋揹埑偼丄
|
倣倁俹亅俹
|
|
嘑
|
俻侾偺僄儈僢僞怣崋揹棳倝倕侾偼丄
乮僄儈僢僞偺僀儞僺乕僟儞僗偼嘍偱偁偭偨偐傜丄乯
|
倣俙俹亅俹
|
|
嘒
|
俻俀偺僐儗僋僞怣崋揹棳偼丄
|
倣俙俹亅俹
|
|
嘓
|
俻俀偺晧壸掞峈俼俴俀偺椉抂揹埑偼丄
|
倁俹亅俹
|
|
嘔
|
怣崋弌椡揹埑倴倧俀偼丄
|
倁俹亅俹
|
俀俇.俉. 摎
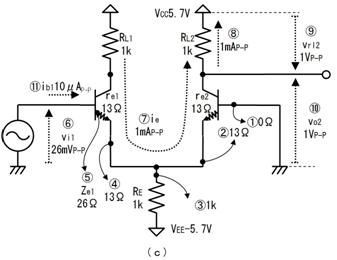
|
斣崋
|
幙栤
|
抣
|
|
|
俻侾偺僄儈僢僞僀儞僺乕僟儞僗傪専摙偟傑偡丅
|
|
|
嘆
|
俻俀偺儀乕僗偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
侽兌
|
|
嘇
|
俻俀偺僄儈僢僞偐傜傾乕僗傪尒偨僀儞僺乕僟儞僗偼丄
|
侾俁兌
|
|
嘊
|
僄儈僢僞掞峈俼俤偐傜儅僀僫僗揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
侾倠兌
|
|
嘋
|
俻侾偺僄儈僢僞偐傜塃懁傪尒偨僀儞僺乕僟儞僗偼丄
乮嘇偲嘊偑暲楍偵尒偊偰乯
|
侾俁兌
|
|
嘍
|
俻侾偺倰倕偺晅偗崻乮儀乕僗偺棤懁乯偐傜塃傪尒偨僀儞僺乕僟儞僗偼丄
|
俀俇兌
|
|
|
夞楬傪岎棳専摙偟傑偡丅
|
|
|
嘐
|
俻侾偺儀乕僗偵壛傢傞怣崋揹埑偼丄
|
俀俇倣倁俹亅俹
|
|
嘑
|
俻侾偺僄儈僢僞怣崋揹棳倝倕侾偼丄
乮僄儈僢僞偺僀儞僺乕僟儞僗偼嘍偱偁偭偨偐傜丄乯
|
侾倣俙俹亅俹
|
|
嘒
|
俻俀偺僐儗僋僞怣崋揹棳偼丄
|
侾倣俙俹亅俹
|
|
嘓
|
俻俀偺晧壸掞峈俼俴俀偺椉抂揹埑偼丄
|
侾倁俹亅俹
|
|
嘔
|
怣崋弌椡揹埑倴倧俀偼丄
|
侾倁俹亅俹
|
壓恾乮倎乯偺傛偆偵丄嵎摦憹暆夞楬偼嵍塃偺儀乕僗傪摨帪偵擖椡偵巊梡偱偒傑偡丅嵍偺儀乕僗偺揹埑傪忋偘傞偲弌椡揹埑偑忋偑傝丄塃偺儀乕僗偺揹埑傪忋偘傞偲弌椡揹埑偑壓偑傝傑偡丅偙偺偨傔丄嵍偺儀乕僗傪亄擖椡丄塃偺儀乕僗傪亅擖椡偲屇傃傑偡丅
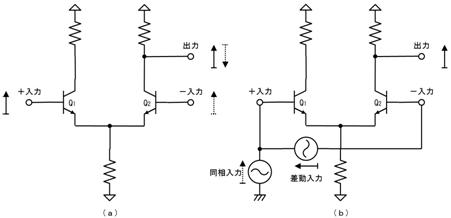
忋恾乮倐乯偺傛偆偵亄擖椡偲亅擖椡偺娫偵壛偊傞擖椡傪乽嵎摦擖椡乿丄亄擖椡偲亅擖椡傪摨帪偵忋壓偝偣傞傛偆側擖椡傪乽摨憡擖椡乿偲屇傃傑偡丅嵎摦憹暆夞楬偼丄嵎摦擖椡偩偗傪憹暆偟偰弌椡偟傑偡丅
嵎摦憹暆夞楬偼埨掕偟偰偍傝憹暆棪傕戝偒偄偱偡偑丄弌椡僀儞僺乕僟儞僗偑崅偄偺偱丄壓恾偵帵偡傛偆偵丄弌椡偵僄儈僢僞僼僅儘傾傪捛壛偟偰巊梡偟傑偡丅
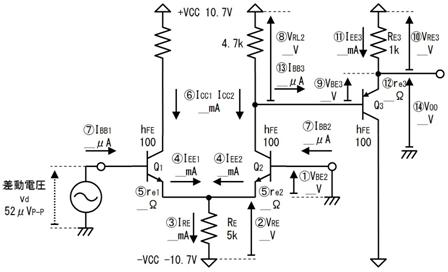
俀俈.侾. 楙廗
忋恾偺夞楬傪壓昞偵彂偒崬傒側偑傜捈棳専摙偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻俀偺倁俛俤偼丄
|
倁
|
|
嘇
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
|
倁
|
|
嘊
|
僄儈僢僞掞峈偵棳傟傞揹棳俬俼俤偼丄
|
倣俙
|
|
嘋
|
俻侾偲俻俀偺僄儈僢僞僶僀傾僗揹棳俬俤俤侾丄俬俤俤俀偼丄
|
倣俙
|
|
嘍
|
俻侾偲俻俀偺僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕侾丄倰倕俀偼丄
|
兌
|
|
嘐
|
俻侾偲俻俀偺僐儗僋僞僶僀傾僗揹棳俬俠俠侾丄俬俠俠俀偼丄
|
倣俙
|
|
嘑
|
俻侾偲俻俀偺儀乕僗僶僀傾僗揹棳俬俛俛侾丄俬俛俛俀偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
兪俙
|
|
嘒
|
俻俀偺晧壸掞峈俼俴俀偺椉抂揹埑偼丄
|
倁
|
|
嘓
|
俻俁偺倁俛俤偼丄
|
倁
|
|
嘔
|
俻俁偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤俁偼丄
|
倁
|
|
嘕
|
俻俁偺僄儈僢僞僶僀傾僗揹棳俬俤俤俁偼丄
|
倣俙
|
|
嘖
|
俻俁偺僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕俁偼丄
|
兌
|
|
嘗
|
俻俁偺儀乕僗僶僀傾僗揹棳俬俛俛俁偼丄
|
兪俙
|
|
|
慜抜偺僐儗僋僞僶僀傾僗揹棳偼俬俠俠俀偼屻抜偺儀乕僗僶僀傾僗揹棳俬俛俛俁偺壗攞丄
乮俻俁偺倛俥俤偽傜偮偒偺塭嬁傪旔偗傞偨傔丄俀侽攞掱搙梸偟偄乯
|
攞
|
|
嘙
|
弌椡僶僀傾僗揹埑倁俷俷偼丄
|
倁
|
俀俈.俀. 摎
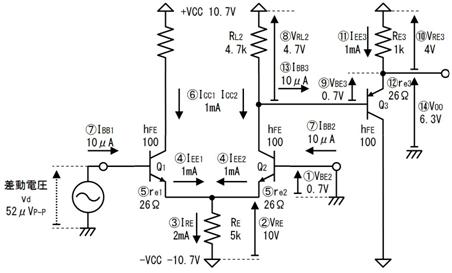
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻俀偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘇
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
|
侾侽倁
|
|
嘊
|
僄儈僢僞掞峈偵棳傟傞揹棳俬俼俤偼丄
|
俀倣俙
|
|
嘋
|
俻侾偲俻俀偺僄儈僢僞僶僀傾僗揹棳俬俤俤侾丄俬俤俤俀偼丄
|
侾倣俙
|
|
嘍
|
俻侾偲俻俀偺僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕侾丄倰倕俀偼丄
|
俀俇兌
|
|
嘐
|
俻侾偲俻俀偺僐儗僋僞僶僀傾僗揹棳俬俠俠侾丄俬俠俠俀偼丄
|
侾倣俙
|
|
嘑
|
俻侾偲俻俀偺儀乕僗僶僀傾僗揹棳俬俛俛侾丄俬俛俛俀偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
侾侽兪俙
|
|
嘒
|
俻俀偺晧壸掞峈俼俴俀偺椉抂揹埑偼丄
|
係丏俈倁
|
|
嘓
|
俻俁偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘔
|
俻俁偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤俁偼丄
|
係倁
|
|
嘕
|
俻俁偺僄儈僢僞僶僀傾僗揹棳俬俤俤俁偼丄
|
侾倣俙
|
|
嘖
|
俻俁偺僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕俁偼丄
|
俀俇兌
|
|
嘗
|
俻俁偺儀乕僗僶僀傾僗揹棳俬俛俛俁偼丄
|
侾侽兪俙
|
|
|
慜抜偺僐儗僋僞僶僀傾僗揹棳偼俬俠俠俀偼屻抜偺儀乕僗僶僀傾僗揹棳俬俛俛俁偺壗攞丄
乮俻俁偺倛俥俤偽傜偮偒偺塭嬁傪旔偗傞偨傔丄俀侽攞掱搙梸偟偄乯
|
侾侽侽攞
|
|
嘙
|
弌椡僶僀傾僗揹埑倁俷俷偼丄
|
俇丏俁倁
|
俀俈.俁. 楙廗
壓恾傪嶲峫偵壓昞偵彂偒崬傒側偑傜壓恾偺夞楬傪岎棳専摙偟偰丄揹埑憹暆棪偲弌椡僀儞僺乕僟儞僗傪媮傔偰偔偩偝偄丅
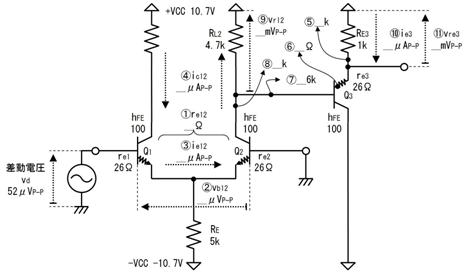
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺儀乕僗偲俻俀偺儀乕僗娫偺怣崋揹埑倴倐侾俀偼丄
|
兪倁俹亅俹
|
|
嘇
|
俻侾偲俻俀偺僄儈僢僞懁僀儞僺乕僟儞僗偺崌寁偼丄
|
兌
|
|
嘊
|
俻侾偲俻俀偺僄儈僢僞怣崋揹棳倝倕侾俀偼丄
|
兪俙俹亅俹
|
|
嘋
|
俻侾偲俻俀偺僐儗僋僞怣崋揹棳倝們侾俀偼丄
乮曽岦偼屳偄偵堎側傞偑丄乯
|
兪俙俹亅俹
|
|
嘍
|
俼俤俁偺壓懁偐傜亄揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
倠兌
|
|
嘐
|
俻俁偺儀乕僗偺棤懁偐傜丄亄揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
兌
|
|
嘑
|
俻俁偺儀乕僗偐傜亄揹尮傪尒偨僀儞僺乕僟儞僗偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
倠兌
|
|
嘒
|
俻俀偺僐儗僋僞偐傜亄揹尮傪尒偨僀儞僺乕僟儞僗偼丄
乮俼俴俀偲嘑偑暲楍偵尒偊偰丄乯
|
倠兌
|
|
嘓
|
俻俀偺晧壸掞峈俼俴俀偺椉抂怣崋揹埑偼丄
乮嘋偲嘒偐傜丄乯
|
倣倁俹亅俹
|
|
嘔
|
俻俁偺僄儈僢僞怣崋揹埑倝倕俁偼丄
|
兪俙俹亅俹
|
|
嘕
|
俼俤俁偺椉抂怣崋揹埑偼丄
|
倣倁俹亅俹
|
|
|
揹埑憹暆棪俙倴偼丄
乮嘇偲嘕偐傜丄乯
|
攞
|
|
|
弌椡僀儞僺乕僟儞僗偼丄
乮乮俼俴俀乛倛俥俤俁亄俀俇兌乯乛乛侾倠兌偱丄乯
|
兌
|
俀俈.係. 摎
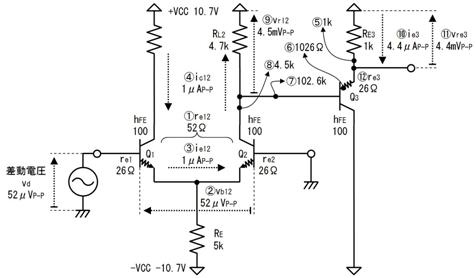
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺儀乕僗偲俻俀偺儀乕僗娫偺怣崋揹埑倴倐侾俀偼丄
|
俆俀兪倁俹亅俹
|
|
嘇
|
俻侾偲俻俀偺僄儈僢僞懁僀儞僺乕僟儞僗偺崌寁偼丄
|
俆俀兌
|
|
嘊
|
俻侾偲俻俀偺僄儈僢僞怣崋揹棳倝倕侾俀偼丄
|
侾兪俙俹亅俹
|
|
嘋
|
俻侾偲俻俀偺僐儗僋僞怣崋揹棳倝們侾俀偼丄
乮曽岦偼屳偄偵堎側傞偑丄乯
|
侾兪俙俹亅俹
|
|
嘍
|
俼俤俁偺壓懁偐傜亄揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
侾倠兌
|
|
嘐
|
俻俁偺儀乕僗偺棤懁偐傜丄亄揹尮傪尒偨僀儞僺乕僟儞僗偼丄
|
侾侽俀俇兌
|
|
嘑
|
俻俁偺儀乕僗偐傜亄揹尮傪尒偨僀儞僺乕僟儞僗偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
侾侽俀丏俇倠兌
|
|
嘒
|
俻俀偺僐儗僋僞偐傜亄揹尮傪尒偨僀儞僺乕僟儞僗偼丄
乮俼俴俀偲嘑偑暲楍偵尒偊偰丄乯
|
係丏俆倠兌
|
|
嘓
|
俻俀偺晧壸掞峈俼俴俀偺椉抂怣崋揹埑偼丄
乮嘋偲嘒偐傜丄乯
|
係丏俆倣倁俹亅俹
|
|
嘔
|
俻俁偺僄儈僢僞怣崋揹埑倝倕俁偼丄
|
係丏係兪俙俹亅俹
|
|
嘕
|
俼俤俁偺椉抂怣崋揹埑偼丄
|
係丏係倣倁俹亅俹
|
|
|
揹埑憹暆棪俙倴偼丄
乮嘇偲嘕偐傜丄乯
|
俉俆攞
|
|
|
弌椡僀儞僺乕僟儞僗偼丄
乮乮俼俴俀乛倛俥俤俁亄俀俇乯乛乛侾倠兌偱丄乯
|
俇俉兌
|
嵎摦憹暆夞楬偵擻摦晧壸傪墳梡偡傞応崌丄壓恾偺傛偆偵丄僄儈僢僞懁偲僐儗僋僞懁偵俀偮偺僇儗儞僩儈儔乕傪巊梡偟傑偡丅偙傟偵傛偭偰摨憡擖椡揹埑偺塭嬁偑堦憌彮側偔側傝丄傑偨丄戝偒側憹暆棪偑摼傜傟傑偡丅
俻侾丄俻俀偑嵎摦憹暆夞楬丄俻俆丄俻俇偑嵎摦憹暆夞楬偺僄儈僢僞揹棳傪堦掕偵曐偮僇儗儞僩儈儔乕丄俻俁丄俻係偑嵎摦憹暆夞楬偺僐儗僋僞揹棳傪摍偟偔曐偮僇儗儞僩儈儔乕偱偡丅
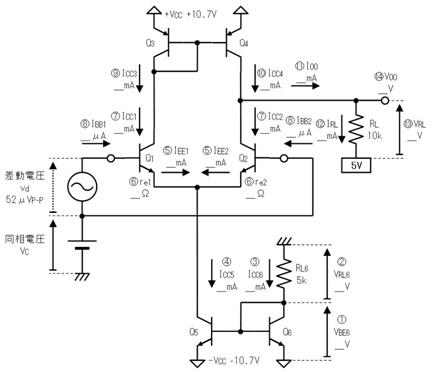
俀俉.侾. 楙廗
忋恾傪嶲峫偵壓昞偵彂偒崬傫偱擻摦晧壸傪棙梡偟偨嵎摦憹暆夞楬傪捈棳専摙偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻俇偺倁俛俤偼丄
|
倁
|
|
嘇
|
晧壸掞峈俼俴俇偺椉抂揹埑偼丄
|
倁
|
|
嘊
|
俻俇偺僐儗僋僞僶僀傾僗揹棳俬俠俠俇偼丄
|
倣俙
|
|
嘋
|
俻俆偺僐儗僋僞僶僀傾僗揹棳俬俠俠俆偼丄
乮俻俆丄俻俇偼僇儗儞僩儈儔乕偩偐傜丄乯
|
倣俙
|
|
嘍
|
俻侾偲俻俀偺僄儈僢僞揹棳俬俤俤侾偲俬俤俤俀偼丄
|
倣俙
|
|
嘐
|
俻侾偲俻俀偺僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕侾偲倰倕俀偼丄
|
兌
|
|
嘑
|
俻侾偲俻俀偺僐儗僋僞僶僀傾僗揹棳俬俠俠侾偲俬俠俠俀偼丄
|
倣俙
|
|
嘒
|
俻侾偲俻俀偺儀乕僗僶僀傾僗揹棳俬俛俛侾偲俬俛俛俀偼丄
|
兪俙
|
|
嘓
|
俻俁偺僐儗僋僞揹棳俬俠俠俁偼丄
|
倣俙
|
|
嘔
|
俻係偺僐儗僋僞揹棳偼丄
乮俻俁丄俻係偼僇儗儞僩儈儔乕偩偐傜丄乯
|
倣俙
|
|
嘕
|
弌椡抂巕傊岦偐偆僶僀傾僗揹棳俬俷俷偼丄
乮嘑偲嘔偐傜丄乯
|
倣俙
|
|
嘖
|
俼俴偵棳傟傞僶僀傾僗揹棳俬俼俴偼丄
|
倣俙
|
|
嘗
|
俼俴偺椉抂揹埑倁俼俴偼丄
|
倁
|
|
嘙
|
弌椡僶僀傾僗揹埑倁俷俷偼丄
|
倁
|
俀俉.俀. 摎
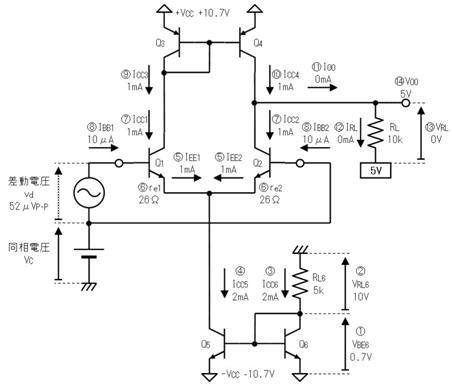
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻俇偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘇
|
晧壸掞峈俼俴俇偺椉抂揹埑偼丄
|
侾侽倁
|
|
嘊
|
俻俇偺僐儗僋僞僶僀傾僗揹棳俬俠俠俇偼丄
|
俀倣俙
|
|
嘋
|
俻俆偺僐儗僋僞僶僀傾僗揹棳俬俠俠俆偼丄
乮俻俆丄俻俇偼僇儗儞僩儈儔乕偩偐傜丄乯
|
俀倣俙
|
|
嘍
|
俻侾偲俻俀偺僄儈僢僞揹棳俬俤俤侾偲俬俤俤俀偼丄
|
侾倣俙
|
|
嘐
|
俻侾偲俻俀偺僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕侾偲倰倕俀偼丄
|
俀俇兌
|
|
嘑
|
俻侾偲俻俀偺僐儗僋僞僶僀傾僗揹棳俬俠俠侾偲俬俠俠俀偼丄
|
侾倣俙
|
|
嘒
|
俻侾偲俻俀偺儀乕僗僶僀傾僗揹棳俬俛俛侾偲俬俛俛俀偼丄
|
侾侽兪俙
|
|
嘓
|
俻俁偺僐儗僋僞揹棳俬俠俠俁偼丄
|
侾倣俙
|
|
嘔
|
俻係偺僐儗僋僞揹棳偼丄
乮俻俁丄俻係偼僇儗儞僩儈儔乕偩偐傜丄乯
|
侾倣俙
|
|
嘕
|
弌椡抂巕傊岦偐偆僶僀傾僗揹棳俬俷俷偼丄
乮嘑偲嘔偐傜丄乯
|
侽倣俙
|
|
嘖
|
俼俴偵棳傟傞僶僀傾僗揹棳俬俼俴偼丄
|
侽倣俙
|
|
嘗
|
俼俴偺椉抂揹埑倁俼俴偼丄
|
侽倁
|
|
嘙
|
弌椡僶僀傾僗揹埑倁俷俷偼丄
|
俆倁
|
偙偺傛偆偵夞楬偺摦嶌偼忋恾偵揹抮偱帵偡摨憡擖椡揹埑倁俠偺塭嬁傪庴偗傑偣傫丅
俀俉.俁. 楙廗
壓恾傪嶲峫偵壓昞偵婰擖偟側偑傜丄夞楬傪岎棳専摙偟偰憹暆棪傪媮傔偰壓偝偄丅
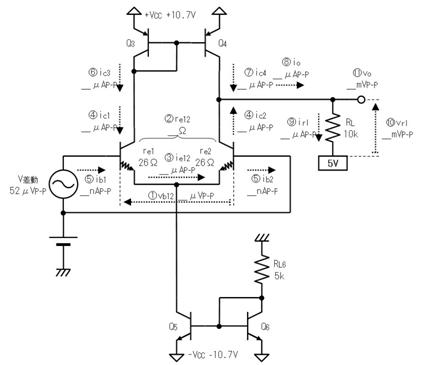
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偲俻俀偺儀乕僗娫偵壛傢傞怣崋揹埑倴倐侾俀偼丄
|
兪倁俹亅俹
|
|
嘇
|
俻侾偲俻俀偺僄儈僢僞懁僀儞僺乕僟儞僗偺崌寁偼丄
|
兌
|
|
嘊
|
俻侾偲俻俀偺僄儈僢僞怣崋揹棳倝倕侾俀偼丄
|
兪俙俹亅俹
|
|
嘋
|
俻侾偲俻俀偺僐儗僋僞怣崋揹棳偼倝們侾丄倝們俀偼丄
乮偦傟偧傟岦偒偼堘偆偑丄乯
|
兪俙俹亅俹
|
|
嘍
|
俻侾偲俻俀偺儀乕僗怣崋揹棳倝倐侾丄倝倐俀偼丄
乮倛俥俤傪侾侽侽偲偡傟偽丄乯
|
値俙俹亅俹
|
|
嘐
|
俻俁偺僐儗僋僞怣崋揹棳倝們俁偼丄
|
兪俙俹亅俹
|
|
嘑
|
俻係偺僐儗僋僞怣崋揹棳倝們係偼丄
乮俻俁丄俻係偼僇儗儞僩儈儔乕偩偐傜丄乯
|
兪俙俹亅俹
|
|
嘒
|
弌椡抂巕傊岦偐偆怣崋揹棳倝倧偼丄
|
兪俙俹亅俹
|
|
嘓
|
晧壸掞峈俼俴偵棳傟傞怣崋揹棳倝倰倢偼丄
|
兪俙俹亅俹
|
|
嘔
|
晧壸掞峈俼俴偺椉抂怣崋揹埑倴倰倢偼丄
|
倣倁俹亅俹
|
|
嘕
|
弌椡怣崋揹埑倴倧偼丄
|
倣倁俹亅俹
|
|
嘖
|
嵎摦揹埑憹暆棪偼丄
乮嘆偲嘕偐傜丄乯
|
攞
|
俀俉.係. 摎
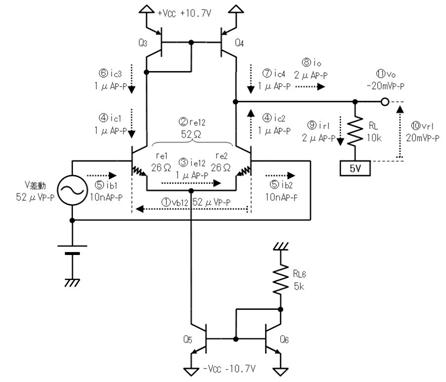
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偲俻俀偺儀乕僗娫偵壛傢傞怣崋揹埑倴倐侾俀偼丄
|
俆俀兪倁俹亅俹
|
|
嘇
|
俻侾偲俻俀偺僄儈僢僞懁僀儞僺乕僟儞僗偺崌寁偼丄
|
俆俀兌
|
|
嘊
|
俻侾偲俻俀偺僄儈僢僞怣崋揹棳倝倕侾俀偼丄
|
侾兪俙俹亅俹
|
|
嘋
|
俻侾偲俻俀偺僐儗僋僞怣崋揹棳偼倝們侾丄倝們俀偼丄
乮偦傟偧傟岦偒偼堘偆偑丄乯
|
侾兪俙俹亅俹
|
|
嘍
|
俻侾偲俻俀偺儀乕僗怣崋揹棳倝倐侾丄倝倐俀偼丄
乮倛俥俤傪侾侽侽偲偡傟偽丄乯
|
侾侽値俙俹亅俹
|
|
嘐
|
俻俁偺僐儗僋僞怣崋揹棳倝們俁偼丄
|
侾兪俙俹亅俹
|
|
嘑
|
俻係偺僐儗僋僞怣崋揹棳倝們係偼丄
乮俻俁丄俻係偼僇儗儞僩儈儔乕偩偐傜丄乯
|
侾兪俙俹亅俹
|
|
嘒
|
弌椡抂巕傊岦偐偆怣崋揹棳倝倧偼丄
|
俀兪俙俹亅俹
|
|
嘓
|
晧壸掞峈俼俴偵棳傟傞怣崋揹棳倝倰倢偼丄
|
俀兪俙俹亅俹
|
|
嘔
|
晧壸掞峈俼俴偺椉抂怣崋揹埑倴倰倢偼丄
|
俀侽倣倁俹亅俹
|
|
嘕
|
弌椡怣崋揹埑倴倧偼丄
|
亅俀侽倣倁俹亅俹
|
|
嘖
|
嵎摦揹埑憹暆棪偼丄
乮嘆偲嘕偐傜丄乯
|
俁俉侽攞
|
壓恾偼乮倎乯偼丄俶俹俶僩儔儞僕僗僞偺摦嶌帪偺柾幃恾偱偡丅僄儈僢僞儀乕僗娫偼揹棳偑棳傟傞岦偒偵揹埑偑壛偊傜傟偰偄傑偡乮弴僶僀傾僗乯偑丄儀乕僗僐儗僋僞娫偼揹棳偺棳傟側偄岦偒偵揹埑偑壛偊傜傟偰偄傑偡乮媡僶僀傾僗乯丅偙偺偨傔丄儀乕僗偲僄儈僢僞偺娫偵偼壓恾乮倎乯偵奃怓偱帵偡丄愨墢惈偺嬻朢憌偑弌棃偰偄傑偡丅
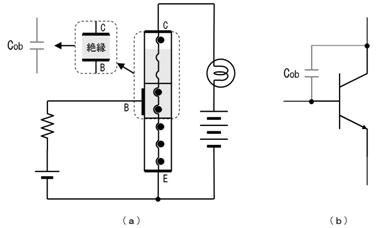
偮傑傝丄忋恾乮倎乯偵揰慄偱埻偭偰帵偡傛偆偵丄僐儗僋僞偲儀乕僗偑愨墢懱偱妘偰傜傟偰偄傞栿偱偡偐傜丄僐儞僨儞僒偲偟偰傕婡擻偟傑偡丅偮傑傝丄忋恾乮倐乯偵帵偡傛偆偵丄僐儗僋僞偲儀乕僗偺娫偵偼丄梕検偑惗偠丄僩儔儞僕僗僞偺惈擻乮慺憗偄摦嶌乯偵戝偒側塭嬁傪梌偊傑偡丅偙偺梕検傪丄僐儗僋僞弌椡梕検乮俠倧倐乯偲屇傃傑偡丅
僩儔儞僕僗僞偵偼俁杮偺抂巕偑偁傝丄壗傟偐侾杮傪擖椡丄偦偺懠偺侾杮傪弌椡偵巊偆偲丄擖椡偱傕弌椡偱傕柍偄抂巕偑侾偮巆傝傑偡丅偙偺巆偭偨堦杮偺抂巕偺柤徧傪巊偭偰丄僩儔儞僕僗僞夞楬偵柤慜傪晅偗乽愙抧曽幃乿偲屇傫偱偄傑偡丅
椺偊偽壓恾乮倎乯偺傛偆偵丄儀乕僗傪擖椡偵丄僐儗僋僞傪弌椡偵巊偆偲丄僄儈僢僞偑巆傞偺偱丄偙偺巊偄曽乮愙抧曽幃乯偼乽僄儈僢僞愙抧乿偲屇傃傑偡丅傑偨丄壓恾乮倐乯偺傛偆偵丄儀乕僗傪擖椡偵丄僄儈僢僞傪弌椡偵巊偆偲丄僐儗僋僞偑巆傞偺偱丄偙偺巊偄曽乮愙抧曽幃乯偼乽僐儗僋僞愙抧乮暿柤僄儈僢僞僼僅儘傾乯乿偲屇傃傑偡丅
僐儗僋僞乽愙抧乿偲偼屇傃傑偡偑丄僐儗僋僞偑乽傾乕僗乿偵愙懕偝傟偰偄傞栿偱偼偁傝傑偣傫丅偁偔傑偱傕乽怣崋傪壛偊偰偄側偄乿偲偄偆婥帩偱乽愙抧乿偲屇傫偱偄傞偩偗偱偡丅偱偡偐傜僐儗僋僞乽嫟捠乿偲屇傇恖傕偄傑偡丅
塸岅偱偼乽common-emitter amplifier乿偱梫偼乽common乿傪乽愙抧乿偲栿偡偐乽嫟捠乿偲栿偡偐偲偄偆栤戣偱偡丅
壓恾偵俁偮偺愙抧曽幃偺棯恾傪帵偟傑偡丅
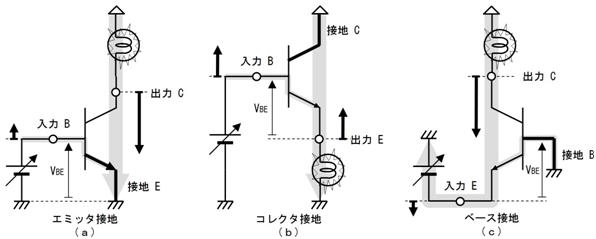
忋恾乮倎乯偺僄儈僢僞愙抧偼丄嬐偐偵擖椡揹埑傪忋偘傞偲弌椡揹埑偑掅壓偟丄戝偒側揹埑憹暆棪偑摼傜傟丄偦偺忋丄擖椡揹棳偼倛俥俤攞偵憹戝偟偰弌椡偵棳傟傑偡丅偮傑傝丄揹埑傕揹棳傕憹暆偱偒傑偡丅
忋恾乮倐乯偺僄儈僢僞愙抧偼丄擖椡揹埑傪侾倁忋偘傞偲丄弌椡揹埑傕侾倁忋偑傝傑偡丅偮傑傝揹埑偼憹暆偝傟傑偣傫丅偟偐偟丄擖椡揹棳偼倛俥俤攞偵憹戝偟偰弌椡偵棳傟傑偡丅偮傑傝丄揹棳偩偗偑憹暆偱偒傑偡丅
忋恾乮們乯偺儀乕僗愙抧偼丄嬐偐偵擖椡揹埑傪壓偘傞偲弌椡揹埑偑掅壓偟丄戝偒側揹埑憹暆棪偑摼傜傟傑偡丅偟偐偟丄擖椡偵棳傟偨揹棳偑偦偺傑傑弌椡偵棳傟丄揹棳偼憹暆偝傟傑偣傫丅
偙傟傜傪傑偲傔傞偲丄壓昞偺傛偆偵側傝傑偡丅
|
愙抧曽幃
|
僄儈僢僞愙抧
|
僐儗僋僞愙抧
|
儀乕僗愙抧
|
|
揹埑憹暆棪
|
戝偒偄
|
侾攞
|
戝偒偄
|
|
揹棳憹暆棪
|
戝偒偄
|
戝偒偄
|
侾攞
|
|
揹椡憹暆棪
揹埑憹暆亊揹棳憹暆
|
戝偒偄
|
暲
|
暲
|
壓恾偵奺夞楬偺擖弌椡僀儞僺乕僟儞僗傪帵偟傑偡丅
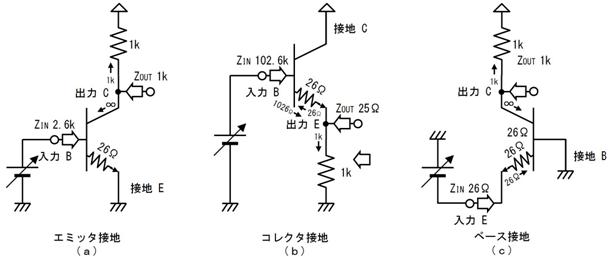
奺夞楬偺擖弌椡僀儞僺乕僟儞僗偼丄壓昞偺傛偆偵側傝傑偡丅
|
愙抧曽幃
|
僄儈僢僞愙抧
|
僐儗僋僞愙抧
|
儀乕僗愙抧
|
|
擖椡僀儞僺乕僟儞僗
|
暲
|
崅偄
|
掅偄
|
|
弌椡僀儞僺乕僟儞僗
|
崅偄
|
掅偄
|
崅偄
|
僐儗僋僞弌椡梕検俠倧倐偺塭嬁偼丄壓恾偺傛偆偵夞楬曽幃偵傛偭偰堎側傝傑偡丅
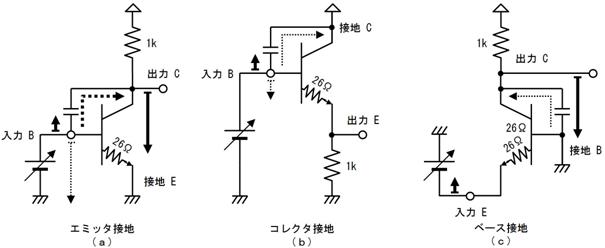
忋恾乮倎乯偺僄儈僢僞愙抧偱偼擖椡揹埑傪彮偟忋偘傞偲丄弌椡偑戝偒偔掅壓偟丄俠倧倐傪捠偠偰乮忋恾偵揰慄偱帵偡乯戝偒側揹棳偑棳傟丄忋偑傠偆偲偡傞擖椡揹埑傪墴偟壓偘傑偡丅偦偺偨傔丄偁偨偐傕戝梕検偺俠倧倐偑懚嵼偡傞傛偆側戝偒側塭嬁偑惗偠傑偡丅偙偺傛偆偵僄儈僢僞愙抧偱俠倧倐偑戝偒偔尒偊傞嶌梡傪乽儈儔乕岠壥乿偲屇傃傑偡丅僄儈僢僞愙抧偼儈儔乕岠壥偑惗偠傞偨傔丄崅偄廃攇悢偺憹暆偑嬯庤偱偡丅
忋恾乮倐乯偺僐儗僋僞愙抧偱偼擖椡揹埑傪忋偘傞偲丄俠倧倐偵揹棳偑棳傟傑偡丅偟偐偟俠倧倐偺堦曽偼揹埑偺曄壔偟側偄揹尮偵愙懕偝傟偰偄傞偺偱丄儈儔乕岠壥偼惗偠傑偣傫丅偙偺傛偆偵丄僐儗僋僞愙抧偱偼俠倧倐偑擖椡偵彫偝側塭嬁傪梌偊傞偨傔丄懡彮崅偄廃攇悢偱傕憹暆偱偒傑偡丅
忋恾乮們乯偺儀乕僗愙抧偱偼丄俠倧倐偑擖椡偵愙懕偝傟偰偄傑偣傫丅偙偺偨傔俠倧倐偼擖椡偵塭嬁傪梌偊偢丄儀乕僗愙抧偼崅偄廃攇悢偺憹暆偑摼堄偱偡丅
偙傟傜傪傑偲傔傞偲壓昞偺傛偆偵側傝傑偡丅
|
愙抧曽幃
|
僄儈僢僞愙抧
|
僐儗僋僞愙抧
|
儀乕僗愙抧
|
|
巊梡偱偒傞廃攇悢
|
掅偄
|
拞掱搙
|
崅偄
|
偙傟傑偱偺愢柧傪傑偲傔傞偲丄壓昞偺傛偆偵側傝傑偡丅
|
愙抧曽幃
|
僄儈僢僞愙抧
|
僐儗僋僞愙抧
|
儀乕僗愙抧
|
|
揹埑憹暆棪
|
戝偒偄
|
侾攞
|
戝偒偄
|
|
揹棳憹暆棪
|
戝偒偄
|
戝偒偄
|
侾攞
|
|
揹椡憹暆棪
|
戝偒偄
|
暲
|
暲
|
|
擖椡僀儞僺乕僟儞僗
|
暲
|
崅偄
|
掅偄
|
|
弌椡僀儞僺乕僟儞僗
|
崅偄
|
掅偄
|
崅偄
|
|
巊梡偱偒傞廃攇悢
|
掅偄
|
拞掱搙
|
崅偄
|
|
暿柤
|
|
僄儈僢僞僼僅儘傾
|
|
僇僗僐乕僪憹暆婍偼丄傛傝崅偄廃攇悢傪憹暆偡傞偨傔偵棙梡偝傟傞夞楬偱偡丅
壓恾乮倎乯偼偁傝傆傟偨僄儈僢僞愙抧偺憹暆婍偱偡丅儈儔乕岠壥偵傛傝俠倧倐偑嫮偔塭嬁偟丄崅偄廃攇悢傪憹暆偡傞偙偲偑偱偒傑偣傫丅
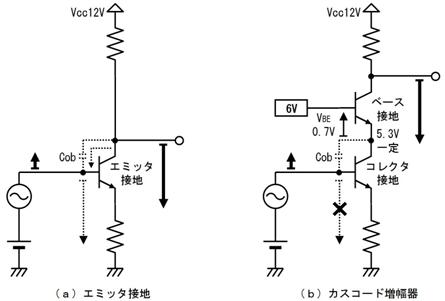
忋恾乮倐乯偼僇僗僐乕僪憹暆婍偱偡丅僄儈僢僞愙抧夞楬偺僐儗僋僞懁偵丄傕偆堦偮僩儔儞僕僗僞偑捛壛偝傟偰偄傑偡丅
忋懁偺僩儔儞僕僗僞偺儀乕僗偼俇倁偵愙懕偝傟偰偄傞偨傔丄僄儈僢僞偺揹埑偼俆丏俁倁偱堦掕偱偡丅偙偺偨傔丄壓懁偺僩儔儞僕僗僞偺僐儗僋僞揹埑偑堦掕偲側傝丄僐儗僋僞愙抧夞楬偲偟偰慺憗偔摦嶌偟傑偡丅傑偨丄忋懁偺僩儔儞僕僗僞偼儀乕僗愙抧夞楬偱偁傞偨傔丄嬌傔偰慺憗偔摦嶌偟傑偡丅
偦偺寢壥僇僗僐乕僪憹暆婍偼晹昳偑憹壛偟傑偡偑丄慺憗偔摦嶌偟丄崅偄廃攇悢傕憹暆偡傞帠偑偱偒傑偡丅
俁侾.侾. 楙廗
壓恾偺僇僗僐乕僪憹暆夞楬傪壓昞偵彂偒崬傒側偑傜捈棳専摙偟偰偔偩偝偄丅
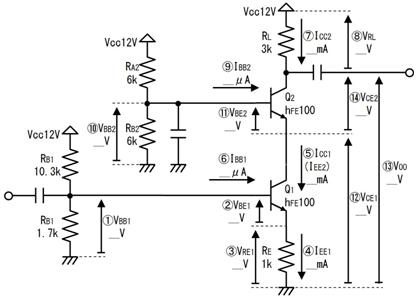
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
暘埑偵傛偭偰摼傜傟傞俻侾偺儀乕僗僶僀傾僗揹埑倁俛俛侾偼丄
|
倁
|
|
嘇
|
俻侾偺倁俛俤偼丄
|
倁
|
|
嘊
|
俻侾偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
|
倁
|
|
嘋
|
俻侾偺僄儈僢僞僶僀傾僗揹棳俬俤俤侾偼丄
|
倣俙
|
|
嘍
|
俻侾偺僐儗僋僞僶僀傾僗揹棳俬俠俠侾乮俻俀偺僄儈僢僞僶僀傾僗揹棳俬俤俤俀乯偼丄
|
倣俙
|
|
嘐
|
俻侾偺儀乕僗僶僀傾僗揹棳俬俛俛侾偼丄
|
兪俙
|
|
嘑
|
俻俀偺僐儗僋僞僶僀傾僗揹棳俬俠俠俀偼丄
|
倣俙
|
|
嘒
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
倁
|
|
嘓
|
俻俀偺儀乕僗僶僀傾僗揹棳俬俛俛俀偼丄
|
兪俙
|
|
嘔
|
暘埑偵傛偭偰摼傜傟傞俻俀偺儀乕僗僶僀傾僗揹埑倁俛俛俀偼丄
|
倁
|
|
嘕
|
俻俀偺倁俛俤偼丄
|
倁
|
|
嘖
|
俻侾偺倁俠俤偼丄
|
倁
|
|
嘗
|
弌椡僶僀傾僗揹埑倁俷俷偼丄
|
倁
|
|
嘙
|
俻俀偺倁俠俤偼丄
|
倁
|
俁侾.俀. 摎
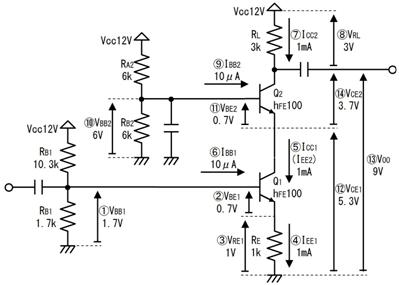
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
暘埑偵傛偭偰摼傜傟傞俻侾偺儀乕僗僶僀傾僗揹埑倁俛俛侾偼丄
|
侾丏俈倁
|
|
嘇
|
俻侾偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘊
|
俻侾偺僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
|
侾倁
|
|
嘋
|
俻侾偺僄儈僢僞僶僀傾僗揹棳俬俤俤侾偼丄
|
侾倣俙
|
|
嘍
|
俻侾偺僐儗僋僞僶僀傾僗揹棳俬俠俠侾乮俻俀偺僄儈僢僞僶僀傾僗揹棳俬俤俤俀乯偼丄
|
侾倣俙
|
|
嘐
|
俻侾偺儀乕僗僶僀傾僗揹棳俬俛俛侾偼丄
|
侾侽兪俙
|
|
嘑
|
俻俀偺僐儗僋僞僶僀傾僗揹棳俬俠俠俀偼丄
|
侾倣俙
|
|
嘒
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
俁倁
|
|
嘓
|
俻俀偺儀乕僗僶僀傾僗揹棳俬俛俛俀偼丄
|
侾侽兪俙
|
|
嘔
|
暘埑偵傛偭偰摼傜傟傞俻俀偺儀乕僗僶僀傾僗揹埑倁俛俛俀偼丄
|
俇倁
|
|
嘕
|
俻俀偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘖
|
俻侾偺倁俠俤偼丄
|
俆丏俁倁
|
|
嘗
|
弌椡僶僀傾僗揹埑倁俷俷偼丄
|
俋倁
|
|
嘙
|
俻俀偺倁俠俤偼丄
|
俁丏俈倁
|
惓妋側揹埑傪摼傞側傜僣僃乕僫僟僀僆乕僪摍偺掅揹埑晹昳傪巊梡偟傑偡偑丄倁俛俤偲摨條偵壏搙偱曄壔偡傞揹埑偑昁梫側応崌偑偁傝傑偡丅偙偺傛偆側応崌偼丄僟僀僆乕僪傪捈楍偵偟偨傝丄偙偙偱愢柧偡傞倁俛俤儅儖僠僾儔僀儎傪巊梡偟傑偡丅
壓恾乮倎乯偺傛偆偵丄僟僀僆乕僪傪捈楍偵偟偰揹棳傪棳偡偙偲偱丄倁俛俤俁屄暘乮栺俀丏侾倁乯偺揹埑傪摼傞偙偲偑偱偒傑偡丅偨偩偟偙偺曽朄偱偼乽俀丏俆屄暘乿偲偄偭偨敿抂側揹埑偼摼傞偙偲偑偱偒傑偣傫丅
忋恾乮倐乯偼丄僩儔儞僕僗僞傪巊偭偰乮倎乯偲帡偨摦嶌傪峴側偆夞楬偱偡丅掞峈抣偺愝掕師戞偱丄倁俛俤俀丏俆屄暘丄摍偺敿抂側攞棪傕巊梡偱偒傑偡丅壓昞偵彂偒崬傫偱夞楬偺忬懺傪妋擣偟偰壓偝偄丅
俁俀.侾. 妋擣
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘇
|
壓懁偺掞峈偵棳傟傞揹棳俬俼俛俤偼丄
|
倣俙
|
|
嘊
|
俬俛傪柍帇偡傟偽丄忋懁偺掞峈偵棳傟傞揹棳俬俼俠俛偼丄
乮僉儖僸懃傛傝乯
|
倣俙
|
|
嘋
|
忋懁偺掞峈偺椉抂揹埑倁俠俛偼丄
|
倁
|
|
嘍
|
慡懱偺揹埑倁俠俤偼丄
|
倁
|
|
嘐
|
僐儗僋僞揹棳俬俠偼丄
乮慡懱偺揹棳偑俁倣俙偩偐傜丄嘊偲僉儖僸懃偱乯
|
倣俙
|
|
嘑
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑侾侽侽偩偐傜乯
|
兪俙
|
|
嘒
|
儀乕僗揹棳傪柍帇偟側偗傟偽丄俬俼俠俛偼丄
|
倣俙
|
|
嘓
|
儀乕僗揹棳傪柍帇偟側偗傟偽丄倁俠俛偼丄
|
倁
|
|
嘔
|
儀乕僗揹棳傪柍帇偟側偗傟偽丄慡懱偺揹埑倁俠俤偼丄
|
倁
|
俁俀.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘇
|
壓懁偺掞峈偵棳傟傞揹棳俬俼俛俤偼丄
|
侾倣俙
|
|
嘊
|
俬俛傪柍帇偡傟偽丄忋懁偺掞峈偵棳傟傞揹棳俬俼俠俛偼丄
乮僉儖僸懃傛傝乯
|
侾倣俙
|
|
嘋
|
忋懁偺掞峈偺椉抂揹埑倁俠俛偼丄
|
侾丏係倁
|
|
嘍
|
慡懱偺揹埑倁俠俤偼丄
|
俀丏侾倁
|
|
嘐
|
僐儗僋僞揹棳俬俠偼丄
乮慡懱偺揹棳偑俁倣俙偩偐傜丄嘊偲僉儖僸懃偱乯
|
俀倣俙
|
|
嘑
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑侾侽侽偩偐傜乯
|
俀侽兪俙
|
|
嘒
|
儀乕僗揹棳傪柍帇偟側偗傟偽丄俬俼俠俛偼丄
|
侾丏侽俀倣俙
|
|
嘓
|
儀乕僗揹棳傪柍帇偟側偗傟偽丄倁俠俛偼丄
|
侾丏係俀俉倁
|
|
嘔
|
儀乕僗揹棳傪柍帇偟側偗傟偽丄慡懱偺揹埑倁俠俤偼丄
|
俀丏侾俀俉倁
|
偙偺傛偆偵丄俬俛傪柍帇偡傟偽丄壓偺掞峈偲忋偺掞峈偱慡懱偺揹埑偑寛傑傝丄
慡懱偺揹埑乮倁俠俤乯
佮 侽丏俈
亄 侽丏俈
亊 俼俠俛
乛 俼俛俤
=0.7+0.7*R1/R2
偲寁嶼偡傞偙偲偑偱偒傑偡丅
忋恾乮倐乯偺夞楬偼丄倁俛俤偑侽丏俈倁側偗傟偽摦嶌偟傑偣傫丅偙偺偨傔偵丄俬俼俛俤偼乮俈侽侽兌偩偐傜乯侾倣俙昁梫偱偡丅僐儗僋僞偵傕懡彮偺揹棳傪棳偡帠傪峫偊傞偲丄夞楬慡懱偵偼嵟掅俀倣俙掱搙乮俬俼俛俤偺俀攞偔傜偄乯偺揹棳傪棳偡昁梫偑偁傝傑偡丅
傑偨忋昞嘑乣嘔偺傛偆偵丄俬俛偑戝偒偔側傞偲摦嶌偑偔傞偄傑偡丅偱偡偐傜丄俬俛偼俬俼俛俤偺侾侽暘偺侾埲壓偵偟傑偡丅偙偺偨傔丄乮倛俥俤傪侾侽侽偲偡傟偽乯俬俠偼俬俼俛俤偺侾侽攞埲壓偵偡傞昁梫偑偁傝傑偡丅
偮傑傝忋恾偺夞楬偼丄夞楬慡懱偵俬俼俛俤偺俀攞乣侾侽攞掱搙偺揹棳傪棳偟偰巊梡偟傑偡丅
俁俀.俁. 楙廗
壓恾偺夞楬偺揹埑傗揹棳傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
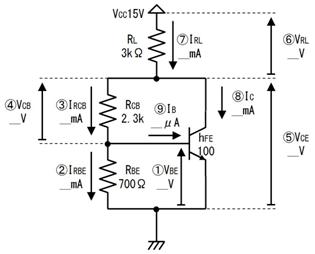
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘇
|
儀乕僗僄儈僢僞娫掞峈偵棳傟傞揹棳俬俼俛俤偼丄
|
倣俙
|
|
嘊
|
儀乕僗揹棳傪柍帇偡傟偽丄僐儗僋僞儀乕僗娫掞峈偵棳傟傞揹棳俬俼俠俛偼丄
|
倣俙
|
|
嘋
|
僐儗僋僞儀乕僗娫揹埑倁俠俛偼丄
|
倁
|
|
嘍
|
僐儗僋僞僄儈僢僞娫揹埑丄倁俠俤偼丄
|
倁
|
|
嘐
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
倁
|
|
嘑
|
晧壸掞峈偵棳傟傞揹棳俬俼俴偼丄
|
倣俙
|
|
嘒
|
僐儗僋僞揹棳俬俠偼丄
乮嘊偲嘑傛傝僉儖僸懃偱丄乯
|
倣俙
|
|
嘓
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
兪俙
|
|
嘔
|
夞楬慡懱偺揹棳俬俼俴偼丄俬俼俛俤偺壗攞丄
|
攞
|
|
嘕
|
俬俼俛俤偺戝偒偝偼揔愗偐丄
乮俀乣侾侽攞側傜揔愗偲峫偊偰丄乯
|
晄揔愗丒揔愗
|
俁俀.係. 摎
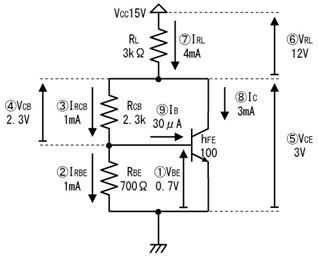
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘇
|
儀乕僗僄儈僢僞娫掞峈偵棳傟傞揹棳俬俼俛俤偼丄
|
侾倣俙
|
|
嘊
|
儀乕僗揹棳傪柍帇偡傟偽丄僐儗僋僞儀乕僗娫掞峈偵棳傟傞揹棳俬俼俠俛偼丄
|
侾倣俙
|
|
嘋
|
僐儗僋僞儀乕僗娫揹埑倁俠俛偼丄
|
俀丏俁倁
|
|
嘍
|
僐儗僋僞僄儈僢僞娫揹埑丄倁俠俤偼丄
|
俁倁
|
|
嘐
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
侾俀倁
|
|
嘑
|
晧壸掞峈偵棳傟傞揹棳俬俼俴偼丄
|
係倣俙
|
|
嘒
|
僐儗僋僞揹棳俬俠偼丄
乮嘊偲嘑傛傝僉儖僸懃偱丄乯
|
俁倣俙
|
|
嘓
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
俁侽兪俙
|
|
嘔
|
夞楬慡懱偺揹棳俬俼俴偼丄俬俼俛俤偺壗攞丄
|
係攞
|
|
嘕
|
俬俼俛俤偺戝偒偝偼揔愗偐丄
乮俀乣侾侽攞側傜揔愗偲峫偊偰丄乯
|
晄揔愗丒揔愗
|
彫怣崋夞楬偱偼丄捈棳揹埑乮僶僀傾僗揹埑乯偵斾傋偰丄岎棳揹埑乮怣崋揹埑乯偑廫暘偵彫偝偄偲峫偊偰丄捈棳偲岎棳傪暘偗偰愝寁偡傞偙偲偑偱偒傑偟偨丅
偟偐偟丄僗僺乕僇乕傪柭傜偡丄儌乕僞乕傪夞偡丄摍偺戝偒側揹椡傪嬱摦偡傞夞楬偱偼丄揹尮揹埑偵嬤偄戝偒側怳暆偺怣崋揹埑傪埖偄傑偡丅偙偺傛偆側夞楬傪揹椡憹暆夞楬偲屇傃傑偡丅
揹椡憹暆夞楬偱偼壓昞偺傛偆偵丄彫怣崋夞楬偲偼堘偆曽朄偱専摙偟丄揹椡傗擬傪専摙偡傞昁梫偑偁傝傑偡丅
|
|
彫怣崋夞楬
|
揹椡憹暆夞楬
|
|
専摙偺曽朄
|
捈棳偲岎棳傪暿乆偵専摙偡傞丅
|
條乆側擖椡乮弌椡乯揹椡偱専摙偡傞丅
偨偲偊偽丄侽倁弌椡帪丄嵟戝揹埑弌椡帪丄拞娫偺揹埑弌椡帪摍
|
|
揹椡
|
夞楬偺徚旓揹椡偼彮側偔丄奺晹昳偺徚旓揹椡傪専摙偡傞昁梫偼彮側偄丅
|
夞楬偺徚旓揹椡偑戝偒偔丄奺晹昳偺徚旓揹椡傪専摙偡傞昁梫偑偁傞丅
|
|
擬
|
擬偺敪惗偼嬐偐偱丄曻擬傪峫偊傞昁梫偼彮側偄丅
|
擬偑敪惗偡傞偨傔丄慺巕偺曻擬傪峫偊傞昁梫偑偁傞丅
|
僩儔儞僕僗僞傪梡偄偨揹椡憹暆夞楬偱偼丄弌椡揹棳偺戝偒側僄儈僢僞僼僅儘傾偑棙梡偝傟傑偡丅壓恾乮倎乯偼俶俹俶僩儔儞僕僗僞傪巊偭偨僄儈僢僞僼僅儘傾偱偡丅亄揹尮偱摦嶌偟丄擖椡揹棳傪倛俥俤攞偟偰揻偒弌偡偙偲偑偱偒傑偡丅弌椡揹埑偼擖椡揹埑傛傝侽丏俈倁掅偔側傝傑偡偑丄擖椡偵廬偭偰曄壔偟傑偡丅傑偨丄壓恾乮倐乯偼俹俶俹僩儔儞僕僗僞傪巊偭偨僄儈僢僞僼僅儘傾偱偡丅亅揹尮偱摦嶌偟丄擖椡揹棳傪倛俥俤攞偟偰媧偄崬傓偙偲偑偱偒傑偡丅弌椡揹埑偼擖椡揹埑傛傝侽丏俈倁崅偔側傝傑偡偑丄擖椡偵廬偭偰曄壔偟傑偡丅晧壸偵棳偡揹棳偺岦偒偑堦曽岦偱椙偄応崌偼丄偙偺傛偆側夞楬偑棙梡偱偒傑偡丅
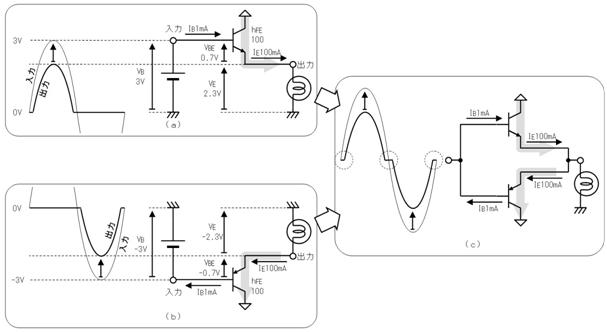
忋恾乮倎乯偲乮倐乯偺夞楬傪堦偮偵偡傞偲丄摨恾乮們乯偵帵偡丄揹棳傪揻偒弌偡偙偲傕丄媧偄崬傓偙偲傕偱偒傞丄僐儞僾儕儊儞僞儕丒僄儈僢僞僼僅儘傾偵側傝傑偡丅
忋恾乮們乯偺夞楬偱偼丄忋懁偺僩儔儞僕僗僞偼擖椡偑侽丏俈倁傛傝掅偄偲偒偼弌椡揹棳偑棳傟傑偣傫丅傑偨丄壓懁偺僩儔儞僕僗僞偼擖椡偑亅侽丏俈倁傛傝崅偄偲偒偼弌椡揹棳偑棳傟傑偣傫丅偙偺偨傔丄擖椡偑亅侽丏俈倁乣侽丏俈倁偺娫偼夞楬偑摦嶌偣偢丄忋恾乮們乯偺僌儔僼偵揰慄偱埻傓晹暘偱攇宍偑榗傓寚揰偑偁傝傑偡丅偙偺榗偼丄忋偺僩儔儞僕僗僞偐傜丄壓偺僩儔儞僕僗僞偵摦嶌偑堷偒宲偑傟傞偲偒偵敪惗偡傞偺偱乽僋儘僗僆乕僶乕榗乿偲屇偽傟傑偡丅
俁係.侾. 楙廗
壓恾偺僄儈僢僞僼僅儘傾夞楬偵丄亄侾侽丏俈倁傪擖椡偟偨応崌偲丄亅俆丏俈倁傪擖椡偟偨応崌偺奺晹偺揹埑傗揹棳傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
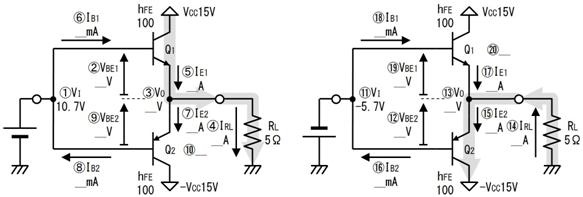
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡偵侾侽丏俈倁傪壛偊偨応崌傪峫偊傑偡丅
|
亅
|
|
嘇
|
俻侾偺儀乕僗僄儈僢僞娫揹埑倁俛俤侾偼丄
乮擖椡揹埑偑僾儔僗偺応崌丄俻侾偵偼揹棳偑棳傟偰偄傞偐傜丄乯
|
倁
|
|
嘊
|
弌椡揹埑倁俷偼丄
|
倁
|
|
嘋
|
晧壸掞峈俼俴偵棳傟傞揹棳俬俼俴偼丄
|
俙
|
|
嘍
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
|
俙
|
|
嘐
|
俻侾偺儀乕僗揹棳俬俛侾偼丄
|
倣俙
|
|
嘑
|
俻俀偺僄儈僢僞揹棳俬俤俀偼丄
|
俙
|
|
嘒
|
俻俀偺儀乕僗揹棳俬俛俀偼丄
|
倣俙
|
|
嘓
|
俻俀偺儀乕僗僄儈僢僞娫揹埑倁俛俤俀偼丄
|
倁
|
|
嘔
|
俻俀偼俷俶偐俷俥俥偐丄乮慖傫偱壓偝偄乯
乮倁俛俤偑晧偺揹埑側傜儀乕僗揹棳偼棳傟側偄偐傜丄乯
|
俷俶丒俷俥俥
|
|
嘕
|
擖椡偵亅俆丏俈倁傪壛偊偨応崌傪峫偊傑偡丅
|
亅
|
|
嘖
|
俻俀偺儀乕僗僄儈僢僞娫揹埑倁俛俤俀偼丄
乮擖椡揹埑偑儅僀僫僗偺応崌丄俻俀偵偼揹棳偑棳傟偰偄傞偐傜丄乯
|
倁
|
|
嘗
|
弌椡揹埑倁俷偼丄
|
倁
|
|
嘙
|
晧壸掞峈俼俴偵棳傟傞揹棳俬俼俴偼丄
|
俙
|
|
嘚
|
俻俀偺僄儈僢僞揹棳俬俤俀偼丄
|
俙
|
|
嘜
|
俻俀偺儀乕僗揹棳俬俛俀偼丄
|
倣俙
|
|
嘝
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
|
俙
|
|
嘠
|
俻侾偺儀乕僗揹棳俬俛侾偼丄
|
倣俙
|
|
嘡
|
俻侾偺儀乕僗僄儈僢僞娫揹埑倁俛俤侾偼丄
|
倁
|
|
嘢
|
俻侾偼俷俶偐俷俥俥偐丄乮慖傫偱壓偝偄乯
乮倁俛俤偑晧偺揹埑側傜儀乕僗揹棳偼棳傟側偄偐傜丄乯
|
俷俶丒俷俥俥
|
俁係.俀. 摎
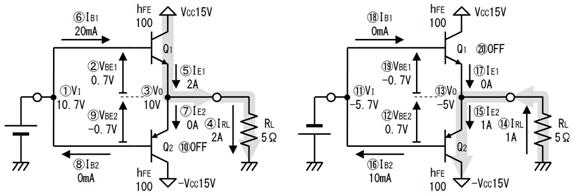
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡偵侾侽丏俈倁傪壛偊偨応崌傪峫偊傑偡丅
|
亅
|
|
嘇
|
俻侾偺儀乕僗僄儈僢僞娫揹埑倁俛俤侾偼丄
乮擖椡揹埑偑僾儔僗偺応崌丄俻侾偵偼揹棳偑棳傟偰偄傞偐傜丄乯
|
侽丏俈倁
|
|
嘊
|
弌椡揹埑倁俷偼丄
|
侾侽倁
|
|
嘋
|
晧壸掞峈俼俴偵棳傟傞揹棳俬俼俴偼丄
|
俀俙
|
|
嘍
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
|
俀俙
|
|
嘐
|
俻侾偺儀乕僗揹棳俬俛侾偼丄
|
俀侽倣俙
|
|
嘑
|
俻俀偺僄儈僢僞揹棳俬俤俀偼丄
|
侽俙
|
|
嘒
|
俻俀偺儀乕僗揹棳俬俛俀偼丄
|
侽倣俙
|
|
嘓
|
俻俀偺儀乕僗僄儈僢僞娫揹埑倁俛俤俀偼丄
|
亅侽丏俈倁
|
|
嘔
|
俻俀偼俷俶偐俷俥俥偐丄乮慖傫偱壓偝偄乯
乮倁俛俤偑晧偺揹埑側傜儀乕僗揹棳偼棳傟側偄偐傜丄乯
|
俷俶丒俷俥俥
|
|
嘕
|
擖椡偵亅俆丏俈倁傪壛偊偨応崌傪峫偊傑偡丅
|
亅
|
|
嘖
|
俻俀偺儀乕僗僄儈僢僞娫揹埑倁俛俤俀偼丄
乮擖椡揹埑偑儅僀僫僗偺応崌丄俻俀偵偼揹棳偑棳傟偰偄傞偐傜丄乯
|
侽丏俈倁
|
|
嘗
|
弌椡揹埑倁俷偼丄
|
亅俆倁
|
|
嘙
|
晧壸掞峈俼俴偵棳傟傞揹棳俬俼俴偼丄
|
侾俙
|
|
嘚
|
俻俀偺僄儈僢僞揹棳俬俤俀偼丄
|
侾俙
|
|
嘜
|
俻俀偺儀乕僗揹棳俬俛俀偼丄
|
侾侽倣俙
|
|
嘝
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
|
侽俙
|
|
嘠
|
俻侾偺儀乕僗揹棳俬俛侾偼丄
|
侽倣俙
|
|
嘡
|
俻侾偺儀乕僗僄儈僢僞娫揹埑倁俛俤侾偼丄
|
亅侽丏俈倁
|
|
嘢
|
俻侾偼俷俶偐俷俥俥偐丄乮慖傫偱壓偝偄乯
乮倁俛俤偑晧偺揹埑側傜儀乕僗揹棳偼棳傟側偄偐傜丄乯
|
俷俶丒俷俥俥
|
偙傟傑偱偵愢柧偟偨壓恾乮倎乯偺夞楬偼丄僋儘僗僆乕僶乕榗傒偑惗偠傑偟偨丅偦偙偱丄壓恾乮倐乯偺傛偆偵僟僀僆乕僪傪捛壛偟偰丄儀乕僗揹埑傪侽丏俈倁崅傔傞偙偲偱乮儀乕僗偵僶僀傾僗揹埑傪壛偊傞偙偲偱乯丄僋儘僗僆乕僶乕榗傪柍偔偡偙偲偑偱偒傑偡丅
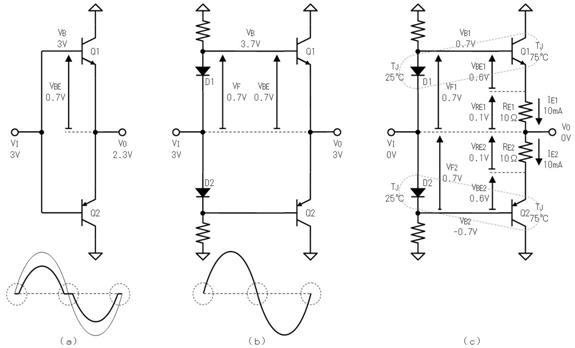
偲偙傠偑丄忋恾乮倐乯偺夞楬偼乽擬朶憱乮僸乕僩儔儞乯乿偲偄偆尰徾偱攋懝偟傑偡丅傑偢丄偦偺巇慻傒傪愢柧偟傑偡丅偙偙偱偼丄擖椡揹埑傕弌椡揹埑傕侽倁応崌傪峫偊傑偡丅
僩儔儞僕僗僞偵偼僟僀僆乕僪傛傝戝偒側揹棳偑棳傟傞偨傔丄敪擬傕戝偒偔側傝傑偡丅偲偙傠偱丄倁俛俤傗倁俥偼侾亷偱俀倣倁掅壓偡傞惈幙偑偁傝傑偡丅偙偺偨傔偨偲偊偽丄僟僀僆乕僪偑俀俆亷偺傑傑偱丄僩儔儞僕僗僞偑俈俆亷偵敪擬偟偨偲偡傞偲丄倁俥偼侽丏俈倁偺傑傑丄倁俛俤偼侽丏俇倁偵掅壓偟傑偡丅偙偺偨傔儀乕僗揹棳偑憹壛偟丄僄儈僢僞揹棳偼偦偺倛俥俤攞偱戝偒偔憹壛偟傑偡丅偦偺寢壥僩儔儞僕僗僞偼偝傜偵敪擬偟丄倁俛俤偼堦憌掅壓偟傑偡丅乮壛偊偰丄倛俥俤偑壏搙偱戝偒偔側傞偲偄偆栤戣傕偁傝傑偡乯
偙偺傛偆偵偟偰丄敪擬仺倁俛俤掅壓仺揹棳憹壛仺峏側傞敪擬丄偲偄偆夁掱傪孞傝曉偟偰丄揹棳偺憹壛丄偁傞偄偼夁擬偱僩儔儞僕僗僞偑攋夡偟傑偡丅偙偺尰徾傪乽擬朶憱乿偲屇傃傑偡丅
師偵擬朶憱偺懳嶔傪愢柧偟傑偡丅庡側懳嶔偼俀偮偁傝傑偡丅侾偮栚偼丄僩儔儞僕僗僞偑敪擬偡傟偽丄僟僀僆乕僪偺壏搙傕忋偑傞傛偆偵乮倁俛俤偑掅壓偡傟偽倁俥偑掅壓偡傞傛偆偵乯偡傞帠偱偡丅偦偺偨傔偵丄僩儔儞僕僗僞偵僟僀僆乕僪傪枾拝乮擬寢崌乯偟傑偡丅偟偐偟丄敿摫懱僠僢僾乮敿摫懱偺杮懱乯偼嬥懏傗僾儔僗僠僢僋偺乮僷僢働乕僕乯梕婍偱暘岤偔曐岇偝傟偰偄傑偡偐傜丄僷僢働乕僕偺昞柺壏搙偼撪晹偺敿摫懱僠僢僾傛傝偐側傝掅偔側傝傑偡丅偙偺偨傔丄擛壗偵偟偭偐傝偲擬寢崌偟偰傕丄僩儔儞僕僗僞偺僠僢僾偲丄僟僀僆乕僪偺僠僢僾傪摨偠壏搙偵偡傞偙偲偼弌棃傑偣傫丅偦偺寢壥丄揹棳偺懡偄僩儔儞僕僗僞偺壏搙偼偳偆偟偰傕僟僀僆乕僪傛傝崅偔側傝丄倁俛俤偼倁俥傛傝掅偔側傝丄揹棳偼偁傞掱搙憹壛偟傑偡丅
偦偙偱丄俀偮栚偺懳嶔傪峴偄傑偡丅俀偮栚偼丄婛偵愢柧偟偨僄儈僢僞掞峈偺憓擖偱偡丅忋恾乮們乯偺傛偆偵丄偨偲偊倁俥偲倁俛俤偵侽丏侾倁偺嵎偑惗偠偰傕丄椺偊偽侾侽兌偺僄儈僢僞掞峈偑憓擖偝傟偰偄傟偽揹棳偼侾侽倣俙憹壛偡傞偩偗偱偡丅偨偩偟丄僄儈僢僞掞峈傪戝偒偔偡傞偲弌椡僀儞僺乕僟儞僗偑忋偑傝丄戝偒側揹棳傪弌椡偱偒側偔側傝傑偡偐傜丄僄儈僢僞掞峈偺抣偼丄擬朶憱偺婋尟偑柍偄斖埻偱彫偝側掞峈抣偵愝掕偟傑偡丅
僄儈僢僞掞峈偺栚埨偼丄僟僀僆乕僪偲僩儔儞僕僗僞偺擬寢崌偑柍偄偲峫偊偰丄徚旓揹椡偺憹壛偱惗偠傞僠僢僾偺壏搙忋徃偼丄儮俿亖儮俹亊俿兤丄壏搙忋徃偱惗偠傞徚旓揹椡偺憹壛偼丄儮俹亖倁俠俠亊儮俿亊俀倣倁乛俼俤丄傛偭偰丄僄儈僢僞掞峈偺嵟掅抣偼丄俼俤乮俵俬俶乯亖倁俠俠亊俿兤亊俀倣倁丄掱搙偱偡丅偨偲偊偽丄倁俠俠侾侽倁偱丄憤擬掞峈俆亷乛倂偺曻擬傪峴偊偽丄俼俤乮俵俬俶乯
亖 侾侽倁 亊 俆亷乛倂 亊
侽丏侽侽俀 亖 侽丏侾兌丄偙偺抣偼乽怢傞偐斀傞偐乿偲偄偆抣偱偡偐傜丄偦偺俁攞偔傜偄偺抣偱丄侽丏俁兌偔傜偄偵愝掕偟傑偡丅傕偪傠傫丄擬寢崌偑廫暘偱偁傟偽掞峈抣偼掅偔偱偒傑偡偑丄偙偺栚埨偼丄倛俥俤偺壏搙偵傛傞忋徃偼攝椂偟偰偄傑偣傫偐傜丄偁傑傝彫偝偔偡傞偙偲偼偱偒傑偣傫丅
壓恾偺僐儞僾儕儊儞僞儕僄儈僢僞僼僅儘傾夞楬偵偮偄偰丄嵟崅揹埑偺弌椡帪偲丄柍怣崋帪偵偮偄偰専摙偟傑偡丅
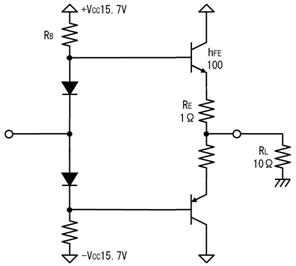
俁係.俁. 楙廗
夞楬偺嵟戝弌椡揹埑傪侾侽倁偲偟偰丄侾侽倁傪弌椡偟偰偄傞応崌偺奺晹偺揹埑傗揹棳傪壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅扐偟丄僩儔儞僕僗僞偺壏搙偑乮俀俆亷偐傜栺俈俆亷偵乯忋徃偟偰丄倁俛俤偑侽丏俇倁偵掅壓偟偰偄傞偲峫偊偰偔偩偝偄丅
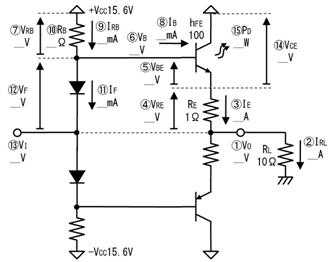
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
弌椡揹埑偼嵟戝抣偺侾侽倁偱偡丅
|
亅
|
|
嘇
|
晧壸掞峈偵棳傟傞揹棳俬俼俴偼丄
|
俙
|
|
嘊
|
僄儈僢僞掞峈偵棳傟傞揹棳俬俼俤偼丄
|
俙
|
|
嘋
|
僄儈僢僞掞峈偺椉抂揹埑俬俼俤偼丄
|
倁
|
|
嘍
|
儀乕僗僄儈僢僞娫揹埑倁俼俤偼丄
|
倁
|
|
嘐
|
儀乕僗揹埑倁俛偼丄
|
倁
|
|
嘑
|
儀乕僗掞峈偺椉抂揹埑倁俼俛偼丄
|
倁
|
|
嘒
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑侾侽侽偩偐傜乯
|
倣俙
|
|
嘓
|
儀乕僗掞峈偺揹棳俬俼俛偼丄
乮儀乕僗揹棳偑偡傋偰儀乕僗掞峈偵棳傟偰偄傞偲偡傟偽丄乯
|
倣俙
|
|
嘔
|
儀乕僗掞峈偺抣偼丄
|
兌
|
|
嘕
|
僟僀僆乕僪偵偼揹棳偑棳傟偰偄側偄偲峫偊傑偡丅
|
亅
|
|
嘖
|
揹棳偺棳傟偰偄側偄僟僀僆乕僪偺椉抂揹埑偼丄
|
倁
|
|
嘗
|
擖椡揹埑偼丄
|
倁
|
|
嘙
|
僐儗僋僞僄儈僢僞娫揹埑倁俠俤偼丄
|
倁
|
|
嘚
|
僩儔儞僕僗僞偺徚旓揹椡俹俢偼丄
|
倂
|
俁係.係. 摎
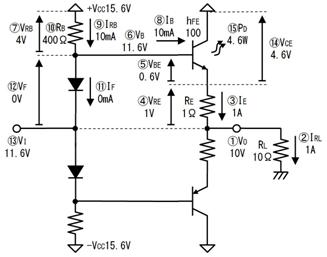
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
弌椡揹埑偼嵟戝抣偺侾侽倁偱偡丅
|
亅
|
|
嘇
|
晧壸掞峈偵棳傟傞揹棳俬俼俴偼丄
|
侾俙
|
|
嘊
|
僄儈僢僞掞峈偵棳傟傞揹棳俬俼俤偼丄
|
侾俙
|
|
嘋
|
僄儈僢僞掞峈偺椉抂揹埑俬俼俤偼丄
|
侾倁
|
|
嘍
|
儀乕僗僄儈僢僞娫揹埑倁俼俤偼丄
|
侽丏俇倁
|
|
嘐
|
儀乕僗揹埑倁俛偼丄
|
侾侾丏俇倁
|
|
嘑
|
儀乕僗掞峈偺椉抂揹埑倁俼俛偼丄
|
係倁
|
|
嘒
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑侾侽侽偩偐傜乯
|
侾侽倣俙
|
|
嘓
|
儀乕僗掞峈偺揹棳俬俼俛偼丄
乮儀乕僗揹棳偑偡傋偰儀乕僗掞峈偵棳傟偰偄傞偲偡傟偽丄乯
|
侾侽倣俙
|
|
嘔
|
儀乕僗掞峈偺抣偼丄
|
係侽侽兌
|
|
嘕
|
僟僀僆乕僪偵偼揹棳偑棳傟偰偄側偄偲峫偊傑偡丅
|
亅
|
|
嘖
|
揹棳偺棳傟偰偄側偄僟僀僆乕僪偺椉抂揹埑偼丄
|
侽倁
|
|
嘗
|
擖椡揹埑偼丄
|
侾侾丏俇倁
|
|
嘙
|
僐儗僋僞僄儈僢僞娫揹埑倁俠俤偼丄
|
係丏俇倁
|
|
嘚
|
僩儔儞僕僗僞偺徚旓揹椡俹俢偼丄
|
係丏俇倂
|
夞楬偺柍怣崋帪偺忬懺偲偟偰丄侽倁傪弌椡偟偰偄傞応崌偺奺晹偺揹埑傗揹棳傪壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅扐偟丄僩儔儞僕僗僞偺壏搙偑乮俀俆亷偐傜栺俈俆亷偵乯忋徃偟偰丄倁俛俤偑侽丏俇倁偵掅壓偟偰偄傞偲峫偊偰偔偩偝偄丅
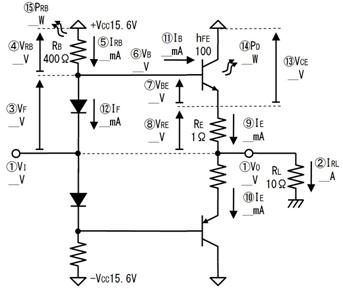
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖弌椡揹埑偼偲傕偵侽倁偲峫偊傑偡丅
|
亅
|
|
嘇
|
晧壸掞峈偵棳傟傞揹棳俬俼俴偼丄
|
俙
|
|
嘊
|
僟僀僆乕僪偺弴曽岦揹埑倁俥偼丄
|
倁
|
|
嘋
|
儀乕僗掞峈偺椉抂揹埑倁俼俛偼丄
|
倁
|
|
嘍
|
儀乕僗掞峈偵棳傟傞揹棳俬俼俛偼丄
乮嘆偲嘊偐傜丄乯
|
倣俙
|
|
嘐
|
儀乕僗揹埑倁俛偼丄
|
倁
|
|
嘑
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
乮壏搙偑忋徃偟偰偄傞偐傜丄乯
|
倁
|
|
嘒
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
乮嘆丄嘊丄嘑偐傜丄乯
|
倁
|
|
嘓
|
僄儈僢僞揹棳俬俤偼丄
|
倣俙
|
|
嘔
|
壓懁偺僩儔儞僕僗僞偺僄儈僢僞揹棳俬俤偼丄
乮嘇偲嘓偐傜丄乯
|
倣俙
|
|
嘕
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
倣俙
|
|
嘖
|
僟僀僆乕僪偺弴揹棳俬俥偼丄
乮嘍偲嘕偐傜僉儖僸懃偱丄乯
|
倣俙
|
|
嘗
|
倁俠俤偼丄
|
倁
|
|
嘙
|
僩儔儞僕僗僞偺徚旓揹椡俹俢偼丄
|
倂
|
|
嘚
|
儀乕僗掞峈偺徚旓揹椡俹俼俛偼丄
乮嘋偲嘍偐傜丄乯
|
倂
|
俁係.俇. 摎
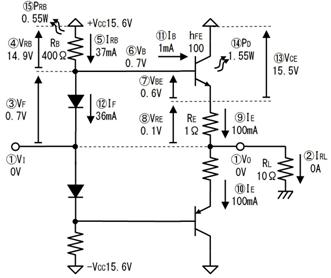
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖弌椡揹埑偼偲傕偵侽倁偲峫偊傑偡丅
|
亅
|
|
嘇
|
晧壸掞峈偵棳傟傞揹棳俬俼俴偼丄
|
侽俙
|
|
嘊
|
僟僀僆乕僪偺弴曽岦揹埑倁俥偼丄
|
侽丏俈倁
|
|
嘋
|
儀乕僗掞峈偺椉抂揹埑倁俼俛偼丄
|
侾係丏俋倁
|
|
嘍
|
儀乕僗掞峈偵棳傟傞揹棳俬俼俛偼丄
乮嘆偲嘊偐傜丄乯
|
俁俈倣俙
|
|
嘐
|
儀乕僗揹埑倁俛偼丄
|
侽丏俈倁
|
|
嘑
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
乮壏搙偑忋徃偟偰偄傞偐傜丄乯
|
侽丏俇倁
|
|
嘒
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤偼丄
乮嘆丄嘊丄嘑偐傜丄乯
|
侽丏侾倁
|
|
嘓
|
僄儈僢僞揹棳俬俤偼丄
|
侾侽侽倣俙
|
|
嘔
|
壓懁偺僩儔儞僕僗僞偺僄儈僢僞揹棳俬俤偼丄
乮嘇偲嘓偐傜丄乯
|
侾侽侽倣俙
|
|
嘕
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
侾倣俙
|
|
嘖
|
僟僀僆乕僪偺弴揹棳俬俥偼丄
乮嘍偲嘕偐傜僉儖僸懃偱丄乯
|
俁俇倣俙
|
|
嘗
|
倁俠俤偼丄
|
侾俆丏俆倁
|
|
嘙
|
僩儔儞僕僗僞偺徚旓揹椡俹俢偼丄
|
侾丏俆俆倂
|
|
嘚
|
儀乕僗掞峈偺徚旓揹椡俹俼俛偼丄
乮嘋偲嘍偐傜丄乯
|
侽丏俆俆倂
|
僐儞僾儕儊儞僞儕僄儈僢僞僼僅儘傾偱丄柍怣崋帪偵棳傟傞僄儈僢僞乮僐儗僋僞乯揹棳傪乽傾僀僪儕儞僌揹棳乿偲屇傃傑偡丅柍怣崋帪偵偼倁俠俤偑戝偒偄偨傔丄彫偝側傾僀僪儕儞僌揹棳偱傕丄堄奜偲戝偒側敪擬傪惗偠傑偡丅
傑偨丄柍怣崋帪偵偼儀乕僗掞峈偺椉抂揹埑偑戝偒偔側傝丄儀乕僗掞峈偺徚旓揹椡傕侽丏俆俆倂偲戝偒偔丄揹椡梡偺掞峈傪巊偆昁梫偑偁傞偙偲偑暘偐傝傑偡丅
偙偺傛偆偵揹椡憹暆夞楬偱偼丄敪擬偡傞晹昳偑憹偊傞偨傔丄奺晹昳偺徚旓揹椡傪寁嶼偟偰夞楬傪専摙偟丄揹椡偵懴偊傞晹昳傪慖傇昁梫偑偁傝傑偡丅
俁俆. 僟乕儕儞僩儞愙懕
壓恾乮倎乯偺夞楬偼僄儈僢僞僼僅儘傾偱偡丅壓恾偺椺偱偼丄擖椡揹棳偺侾侽侽攞偺揹棳傪弌椡偡傞偙偲偑偱偒傑偡丅壓恾乮倐乯偼僄儈僢僞僼僅儘傾傪俀抜愙懕偟偨夞楬偱偡丅擖椡揹棳偑俻侾偱侾侽侽攞丄俻俀偱偝傜偵侾侽侽攞偲側傞偺偱丄俀抜偱擖椡揹棳偺侾侽侽侽侽攞偺揹棳傪弌椡偡傞偙偲偑偱偒傑偡丅
偙偺傛偆偵僄儈僢僞僼僅儘傾傪俀抜廳偹偵偡傞偙偲偱丄慡懱偱倛俥俤侾亊倛俥俤俀偺戝偒側揹棳憹暆棪傪摼傞偙偲偑偱偒傑偡丅
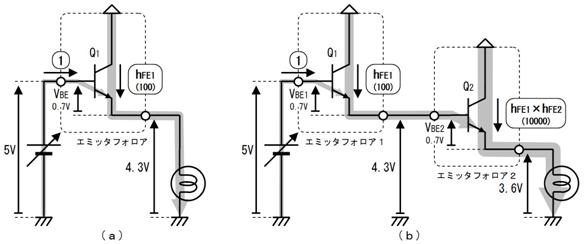
忋恾乮倎乯偺夞楬偺弌椡揹埑偼丄擖椡傛傝侽丏俈倁掅偔側傝丄係丏俁倁偱偡偑丄摨恾乮倐乯偺夞楬偱偼丄侾丏係倁掅偔側傝丄俁丏俇倁偱偡丅偙偺傛偆偵僄儈僢僞僼僅儘傾傪廳偹傞偲丄擖椡偵斾傋偰弌椡揹埑偑掅偔側傝傑偡丅
偲偙傠偱丄壓恾乮倎乯偺俀抜僄儈僢僞僼僅儘傾夞偺俀偮偺僩儔儞僕僗僞傪侾偮偲峫偊偰丄壓恾乮倐乯偺傛偆偵彂偒捈偡偙偲偑偱偒傑偡丅摨恾乮倐乯偺愙懕曽朄傪乽僟乕儕儞僩儞愙懕乿偲屇傃傑偡丅
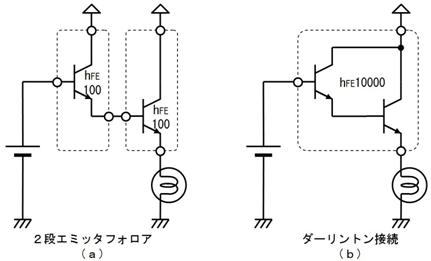
僟乕儕儞僩儞愙懕偟偨僩儔儞僕僗僞偼丄倁俛俤偑侾丏係倁偲戝偒偔側傝傑偡偑丄倛俥俤偼侾侽侽侽侽乮倛俥俤侾亊倛俥俤俀乯偲旕忢偵戝偒偔丄戝揹棳傪弌椡偡傞偺偵曋棙偱偡丅偙偺偨傔丄侾偮偺僷僢働乕僕偵撪晹偱僟乕儕儞僩儞愙懕偟偨俀偮偺僩儔儞僕僗僞傪撪憻偟偨乽僟乕儕儞僩儞僩儔儞僕僗僞乿傕斕攧偝傟偰偄傑偡丅
偝偰丄忋恾偱愢柧偟偨僟乕儕儞僩儞愙懕傪偦偺傑傑巊偆搒丄僩儔儞僕僗僞偑姰慡偵俷俥俥偟傑偣傫丅側偤側傜丄壓恾乮倎乯偺傛偆偵丄僐儗僋僞偐傜儀乕僗偵棳傟偰偒偨俬俠俛俷偺峴偒愭偑柍偔丄俬俠俛俷偑儀乕僗偐傜僄儈僢僞偵棳傟丄偙傟偑倛俥俤攞偝傟偰僐儗僋僞偵棳傟傞偐傜偱偡丅
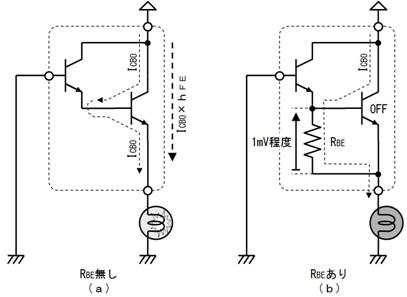
偦偙偱忋恾乮倐乯偺傛偆偵俼俛俤傪庢傝晅偗偰俬俠俛俷偑儀乕僗偵棳傟崬傑側偄傛偆偵偟傑偡丅偙傟偵傛偭偰丄僩儔儞僕僗僞偼姰慡偵俷俥俥偵側傝傑偡丅僗僀僢僠儞僌夞楬偺応崌偲摨條丄俬俠俛俷偵傛偭偰俼俛俤偺椉抂偵惗偠傞揹埑偑侾倣倁掱搙偵側傞傛偆偵俼俛俤傪慖傃傑偡丅
俼俛俤偵偼丄僩儔儞僕僗僞傪姰慡偵俷俥俥偝偣傞栶妱偺傎偐偵傕丄僩儔儞僕僗僞偑俷俥俥偡傞弖娫偵丄儀乕僗偵揹巕傪憲傝崬傓乮揹棳傪儀乕僗偐傜堷偒敳偔乯摥偒傕偁傝傑偡丅乮俹宆偱偁傞儀乕僗偺儂乕儖乮寠乯傪揹巕偱杽傔傞偙偲偱俷俥俥偝偣傑偟偨乯
偙偺偨傔丄俼俛俤傪庢傝晅偗傞偲摦嶌傕慺憗偔側傝丄俼俛俤偺抣偑彫偝偄偲堦憌慺憗偔摦嶌偟傑偡丅偙偺偨傔丄慺憗偔摦嶌偝偣偨偄応崌偼丄忋偺傛偆偵俬俠俛俷偲侾倣倁偐傜寁嶼偟偨抣傛傝丄偝傜偵彫偝側掞峈抣偺俼俛俤偑巊梡偝傟傑偡丅
俁俆.侾. 楙廗
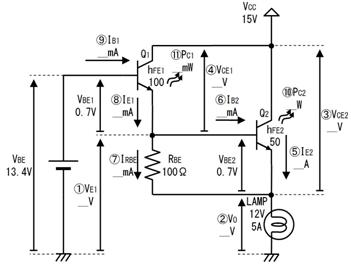
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺僄儈僢僞揹埑倁俤侾偼丄
乮俻侾偺倁俛俤偑侽丏俈倁丄擖椡揹埑偑侾俁丏係倁偩偐傜丄乯
|
倁
|
|
嘇
|
弌椡揹埑倁俷偼丄
乮俻俀偺倁俛俤偑侽丏俈倁偩偐傜丄乯
|
倁
|
|
嘊
|
俻俀偺倁俠俤偼丄
|
倁
|
|
嘋
|
俻侾偺倁俠俤偼丄
|
倁
|
|
嘍
|
揹媴偺巇條傛傝丄俻俀偺僄儈僢僞揹棳俬俤俀偼丄
乮俬俼俛俤偼柍帇偟偰丄乯
|
俙
|
|
嘐
|
俻俀偺儀乕僗揹棳俬俛俀偼丄
乮倛俥俤俀偑俆侽偩偐傜丄乯
|
倣俙
|
|
嘑
|
俼俛俤偵棳傟傞揹棳俬俼俛俤偼丄
|
倣俙
|
|
嘒
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
乮嘐丄嘑偲僉儖僸懃偐傜丄乯
|
倣俙
|
|
嘓
|
俻侾偺儀乕僗揹棳俬俛侾偼丄
乮倛俥俤侾偑侾侽侽偩偐傜丄乯
|
倣俙
|
|
嘔
|
俻俀偺僐儗僋僞懝幐俹俠俀偼丄
|
倂
|
|
嘕
|
俻侾偺僐儗僋僞懝幐俹俠侾偼丄
|
倣俙
|
俁俆.俀. 摎
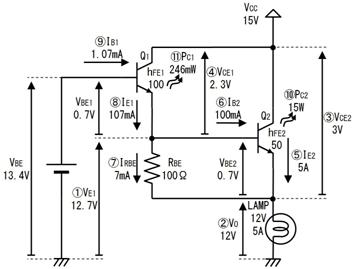
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺僄儈僢僞揹埑倁俤侾偼丄
乮俻侾偺倁俛俤偑侽丏俈倁丄擖椡揹埑偑侾俁丏係倁偩偐傜丄乯
|
侾俀丏俈倁
|
|
嘇
|
弌椡揹埑倁俷偼丄
乮俻俀偺倁俛俤偑侽丏俈倁偩偐傜丄乯
|
侾俀倁
|
|
嘊
|
俻俀偺倁俠俤偼丄
|
俁倁
|
|
嘋
|
俻侾偺倁俠俤偼丄
|
俀丏俁倁
|
|
嘍
|
揹媴偺巇條傛傝丄俻俀偺僄儈僢僞揹棳俬俤俀偼丄
乮俬俼俛俤偼柍帇偟偰丄乯
|
俆俙
|
|
嘐
|
俻俀偺儀乕僗揹棳俬俛俀偼丄
乮倛俥俤俀偑俆侽偩偐傜丄乯
|
侾侽侽倣俙
|
|
嘑
|
俼俛俤偵棳傟傞揹棳俬俼俛俤偼丄
|
俈倣俙
|
|
嘒
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
乮嘐丄嘑偲僉儖僸懃偐傜丄乯
|
侾侽俈倣俙
|
|
嘓
|
俻侾偺儀乕僗揹棳俬俛侾偼丄
乮倛俥俤侾偑侾侽侽偩偐傜丄乯
|
侾丏侽俈倣俙
|
|
嘔
|
俻俀偺僐儗僋僞懝幐俹俠俀偼丄
|
侾俆倂
|
|
嘕
|
俻侾偺僐儗僋僞懝幐俹俠侾偼丄
|
俀係俇倣倂
|
偙偺傛偆偵戝揹棳偺棳傟傞揹椡憹暆夞楬偼丄戝偒側敪擬乮侾俆倂摍乯偑偁傝傑偡丅偟偐偟丄偙偺楙廗偱寁嶼偟偨敪擬偼嵟戝抣偱偼偁傝傑偣傫丅
俻俀偺敪擬偑嵟戝偵側傞偺偼丄倁俠俤偑揹尮揹埑偺敿暘掱搙偵側偭偨偲偒偱偡丅崱夞偺椺偱偼丄俻俀偺倁俠俤偑俈丏俆倁掱搙偺偲偒丄俹俠俀乮俻俀偺敪擬乯偑嵟戝偵側傝傑偡丅
偱偡偐傜偦偺傛偆側忬懺乮倁俠俤偑揹尮揹埑偺敿暘掱搙乯偱傕寁嶼偟丄僐儗僋僞懝幐偑僩儔儞僕僗僞偺嫋梕懝幐傪廫暘偵壓夞偭偰偄傞帠傪妋擣偟傑偡丅傑偨丄僩儔儞僕僗僞扨懱偱偼曻擬偑柍棟側応崌偼丄曻擬婍傪庢傝晅偗傑偡丅
俻侾偵巊偆傛偆側彫宍僩儔儞僕僗僞乮俿俷俋俀僷僢働乕僕乯偼侾倂偺懝幐偱僠僢僾壏搙偑侾侽侽搙忋徃偟傑偡偐傜丄俀係俇倣倂偱偼丄俀係搙忋徃偟丄働乕僗撪壏搙偑俆侽搙側傜僠僢僾偼俈係搙偵側傝傑偡丅乮巊偊傞偱偟傚偆乯
俻俀偵巊偆傛偆側拞宆僩儔儞僕僗僞乮俿俷俀俀侽僷僢働乕僕乯偼侾倂偺懝幐偱僠僢僾壏搙偑俈侽搙忋徃偟傑偡偐傜丄侾俆倂偱偼丄僠僢僾偼侾侽俆侽亷偲側傝丄曻擬婍傪晅偗側偗傟偽妋幚偵夡傟傑偡丅乮僠僢僾偑侾俆侽亷偵側傞偲夡傟傑偡乯
俁俇. 曻擬婍乮僸乕僩僔儞僋乯
僸乕僩僔儞僋偺曻擬擻椡偼擬掞峈偱尰偟傑偡丅壓恾偵乽掞峈乿偲乽擬掞峈乿懳墳傪帵偟傑偡丅
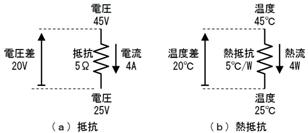
懳墳傪昞偵偡傞偲師昞偺偲偍傝偱偡丅
|
揹婥掞峈
|
擬掞峈
|
|
掞峈偺忋懁偑係俆倁
|
敿摫懱僠僢僾偑係俆亷
|
|
掞峈偺壓懁偑俀俆倁
|
奜婥壏偑俀俆亷
|
|
椉抂揹埑偑俀侽倁
|
壏搙嵎偑俀侽亷
|
|
掞峈抣俼偑俆兌
|
擬掞峈兤偑俆亷乛倂
|
|
棳傟傞揹棳偼係俙
|
曻擬偝傟傞擬偼係倂
|
偱偡偐傜丄
壏搙嵎
亖 曻擬揹椡
亊 擬掞峈
擬掞峈
亖 壏搙嵎
亐 曻擬揹椡
偲寁嶼偱偒傑偡丅
偨偲偊偽丄僐儗僋僞懝幐偑侾侽倂偱丄擬掞峈偑俀亷乛倂側傜丄婥壏偵懳偟偰僠僢僾壏搙偑俆亷崅偔側傝傑偡丅婥壏偑俁侽亷側傜丄僠僢僾偼俁俆亷偱偡丅
擬掞峈偺扨埵偼乵亷乛倂乶偱丄婰崋偵偼兤傗俼俿俫偑椙偔巊傢傟傑偡丅
壓恾偼曻擬婍偺柍偄彫宍僷僢働乕僕偺椺偱偡丅僠僢僾乮愙崌柺倞倳値們倲倝倧値乯偐傜廃埻偺嬻婥乮倎倝倰乯傑偱偺擬掞峈偼兤倞倎偼侾侽侽亷乛倂偱偡丅乮偙偺傛偆偵乽倎偐傜倐傑偱偺擬掞峈乿傪兤倎倐偲彂偒傑偡丅乯
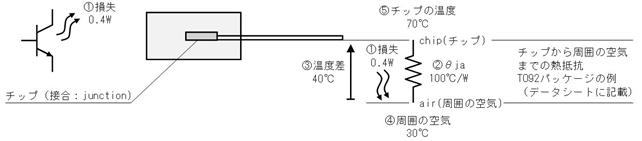
俁俇.侾. 妋擣
忋恾傪嶲峫偵壓昞偵彂偒崬傫偱僠僢僾偺壏搙傪妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僠僢僾偱敪惗偡傞擬乮揹椡丄懝幐乯偼俹俢丄
|
倂
|
|
嘇
|
僠僢僾偐傜廃埻偺嬻婥傑偱偺擬掞峈兤倞倎偼丄
|
亷乛倂
|
|
嘊
|
僠僢僾偲廃埻偺嬻婥偺壏搙嵎偼丄
乮侽丏係倂亊侾侽侽亷乛倂亖係侽亱乯
|
亷
|
|
嘋
|
廃埻偺嬻婥偺壏搙俿倎偼丄
|
亷
|
|
嘍
|
僠僢僾偺壏搙俿倞偼丄
乮嘊偲嘋偐傜丄乯
|
亷
|
俁俇.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僠僢僾偱敪惗偡傞擬乮揹椡丄懝幐乯偼俹俢丄
|
侽丏係倂
|
|
嘇
|
僠僢僾偐傜廃埻偺嬻婥傑偱偺擬掞峈兤倞倎偼丄
|
侾侽侽亷乛倂
|
|
嘊
|
僠僢僾偲廃埻偺嬻婥偺壏搙嵎偼丄
乮侽丏係倂亊侾侽侽亷乛倂亖係侽亱乯
|
係侽亷
|
|
嘋
|
廃埻偺嬻婥偺壏搙俿倎偼丄
|
俁侽亷
|
|
嘍
|
僠僢僾偺壏搙俿倞偼丄
乮嘊偲嘋偐傜丄乯
|
俈侽亷
|
僨乕僞僔乕僩偵彂偐傟偨擬掞峈偵偼丄壓昞偺傛偆偵丄兤倞倎傗兤倞們偑偁傝傑偡丅曻擬婍傪巊傢偢丄慺巕偐傜捈愙曻擬偡傞応崌偼兤倞倎傪巊梡偟傑偡丅
|
婰崋
|
兤倞倎
|
兤倞們
|
|
堄枴
|
僠僢僾乮俹俶愙崌柺丗倞倳値們倲倝倧値乯偐傜丄廃埻偺嬻婥倎倝倰傑偱偺擬掞峈
|
僠僢僾乮俹俶愙崌柺丗倞倳値們倲倝倧値乯偐傜丄働乕僗偺昞柺傑偱偺擬掞峈
|
|
巊偄曽
|
慺巕扨懱偱曻擬偡傞応崌偵棙梡偡傞
|
曻擬婍傪棙梡偟偰曻擬偡傞応崌偵棙梡偡傞丅
|
媡偵丄曻擬婍傪巊梡偡傞応崌偼丄兤倞們傪巊梡偟傑偡丅壓恾偺椺偱偼丄俀倂偑敪惗偡傞僩儔儞僕僗僞傪俀侽倂乛亷偺曻擬婍偵庢傝晅偗偰偄傑偡丅
俁俇.俁. 妋擣
壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜僩儔儞僕僗僞偺僠僢僾壏搙傪媮傔偰偔偩偝偄丅
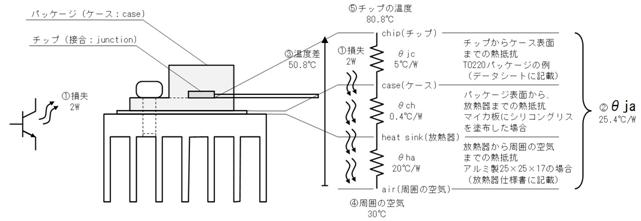
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺懝幐偼俀倂偱偡丅
|
亅
|
|
嘇
|
僩儔儞僕僗僞偺僠僢僾偐傜丄廃埻偺嬻婥傑偱偺擬掞峈偺崌寁偼丄
|
亷乛倂
|
|
嘊
|
懝幐嘆偲擬掞峈嘇偐傜丄壏搙嵎偼丄
|
亷
|
|
嘋
|
廃埻偺嬻婥偺壏搙偼丄
|
亷
|
|
嘍
|
僠僢僾偼丄廃埻偺嬻婥嘋傛傝丄壏搙嵎嘊偩偗擬偔側傞偐傜丄
|
亷
|
俁俇.係. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺懝幐偼俀倂偱偡丅
|
亅
|
|
嘇
|
僩儔儞僕僗僞偺僠僢僾偐傜丄廃埻偺嬻婥傑偱偺擬掞峈偺崌寁偼丄
乮俆亄侽丏係亄俀侽亖俀俆丏係亷乛倂乯
|
俀俆丏係亷乛倂
|
|
嘊
|
懝幐嘆偲擬掞峈嘇偐傜丄壏搙嵎偼丄
乮俀俆丏係亊俀亖俆侽丏俉亷乯
|
俆侽丏俉亷
|
|
嘋
|
廃埻偺嬻婥偺壏搙偼丄
|
俁侽亷
|
|
嘍
|
僠僢僾偼丄廃埻偺嬻婥嘋傛傝丄壏搙嵎嘊偩偗擬偔側傞偐傜丄
俁侽亄俆侽丏俉亖俉侽丏俉亷
|
俉侽丏俉亷
|
僠僢僾偺壏搙偼乮壏搙偵傛傞摿惈偺曄壔偑婥偵側傜側偔偰傕乯侾侽侽搙傪挻偊側偄傛偆偵偟傑偡丅壏搙偑掅偄偲庻柦偑怢傃傑偡乮壏搙偑侾侽亷壓偑傞偲丄庻柦偑攞偵側傞乯偺偱丄挿帩偪偝偣偨偄応崌偼丄掅偄壏搙偱巊梡偟傑偡丅
俁俇.俆. 楙廗
俁丏俉倂偺懝幐傪惗偠傞僩儔儞僕僗僞偺僠僢僾壏搙俿倞傪俉侽亷偵墴偝偊傞偨傔丄偳偺傛偆側曻擬婍偑昁梫偱偡偐丠扐偟丄廃埻壏搙傪係侽亷丄僷僢働乕僕偺擬掞峈傪俆亷乛倂丄愨墢斅偺擬掞峈乮僔儕僐儞僌儕僗揾晍乯傪侽丏係亷乛倂偲偟傑偡丅
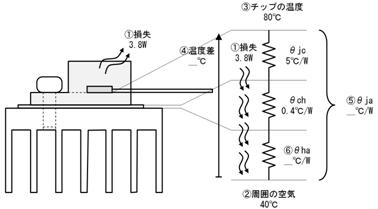
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺懝幐偼俁丏俉倂偱偡丅
|
亅
|
|
嘇
|
僠僢僾偺壏搙偼俉侽亷偵梷偊傑偡丅
|
亅
|
|
嘊
|
廃埻壏搙偼俆侽亷偱偡丅
|
亅
|
|
嘋
|
僠僢僾偲廃埻偺壏搙嵎偼丄
|
亷
|
|
嘍
|
懝幐嘆偲壏搙嵎嘋偐傜丄憤擬掞峈兤倞倎偼丄
|
亷乛倂
|
|
嘐
|
曻擬婍偺擬掞峈偼丄
|
亷乛倂
|
俁俇.俇. 摎
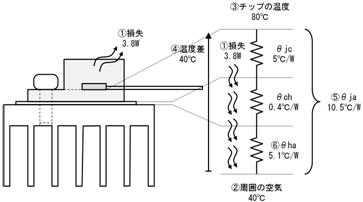
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
僩儔儞僕僗僞偺懝幐偼俁丏俉倂偱偡丅
|
亅
|
|
嘇
|
僠僢僾偺壏搙偼俉侽亷偵梷偊傑偡丅
|
亅
|
|
嘊
|
廃埻壏搙偼俆侽亷偱偡丅
|
亅
|
|
嘋
|
僠僢僾偲廃埻偺壏搙嵎偼丄
|
係侽亷
|
|
嘍
|
懝幐嘆偲壏搙嵎嘋偐傜丄憤擬掞峈兤倞倎偼丄
|
侾侽丏俆亷乛倂
|
|
嘐
|
曻擬婍偺擬掞峈偼丄
憤擬掞峈侾侽丏俆亅働乕僗俆亅愨墢斅侽丏係亷亖曻擬婍俆丏侾亷乛倂
|
俆丏侾亷乛倂
|
僷僢働乕僕乮働乕僗乯偺擬掞峈兤倞們偑戝偒偄偲丄曻擬婍傪偄偔傜戝偒偔偟偰傕娫偵崌傢側偔側傝傑偡丅偙偺傛偆側応崌偼丄傛傝戝偒側僷僢働乕僕乮兤倞們偑彫偝偄乯偺慺巕傪巊梡偟傑偡丅
俁俈. 愙崌宆俥俤俿
俠俷俵俽僆儁傾儞僾偺惈擻偑岦忋偟丄偦偺偆偊埨壙偵側偭偰偄傞偺偱丄愙崌宆俥俤俿乮埲壓丄扨偵乽俥俤俿乿乯傪尛偭偨憹暆婍夞楬偼埲慜傎偳廳梫偱偼偁傝傑偣傫丅偲偼偄偊慺巕偺摿挜傪妶偐偟偰丄偙偙堦敪偲偄偆応強偵巊偆応崌偼偁傝傑偡偐傜丄巇慻傒傗巊偄曽傪愢柧偟傑偡丅
壓恾偵僶僀億乕儔僩儔儞僕僗僞偲俥俤俿偺恾婰崋偲抂巕偺柤慜傪帵偟傑偡丅僩儔儞僕僗僞偱偼丄僄儈僢僞丄僐儗僋僞丄儀乕僗偺奺抂巕偑丄俥俤俿偱偼丄僜乕僗丄僪儗僀儞丄僎乕僩丄偵懳墳偟傑偡丅
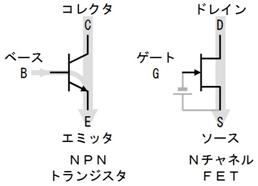
僩儔儞僕僗僞偱偼儀乕僗偵揹棳傪棳偡偙偲偱丄僐儗僋僞偐傜僄儈僢僞偵揹棳偑棳傟傑偡丅偟偐偟丄俥俤俿偱偼僎乕僩偵揹埑傪壛偊傞乮庢傝彍偔乯偙偲偱丄僪儗僀儞偐傜僜乕僗偵揹棳偑棳傟傑偡丅俥俤俿偱偼僎乕僩偵偼揹棳偑棳傟傑偣傫丅
壓恾乮倎乯偵僎乕僩偵揹埑傪壛偊側偄応崌偺俥俤俿偺柾幃恾傪帵偟傑偡丅俶宆敿摫懱傪嫴傓傛偆偵丄俹宆敿摫懱偑攝抲偝傟偰偍傝丄愙崌柺偵偼嬻朢憌偑偱偒偰偄傑偡丅僎乕僩偲僜乕僗偺娫偵揹埑傪壛偊側偄偲偒偼丄嬻朢憌偼嬌敄偄偨傔丄俹宆敿摫懱偵嫴傑傟偨乽僠儍僱儖乿偲屇偽傟傞晹暘偼暆偑峀偔丄僪儗僀儞偐傜僜乕僗偵岦偐偭偰戝偒側揹棳偑棳傟傑偡丅
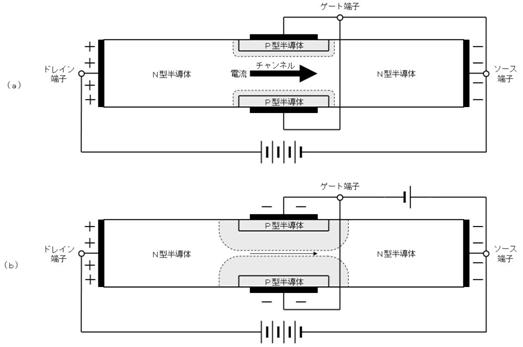
僎乕僩偲僜乕僗偺娫偵晧偺揹埑傪壛偊傞偲忋恾乮倐乯偺傛偆偵嬻朢憌偑峀偑傝丄僠儍僱儖偑嫹偔側傝傑偡丅偦偺寢壥僪儗僀儞偐傜僜乕僗偵棳傟傞揹棳偼尭彮偟傑偡丅偝傜偵僎乕僩偺晧揹埑偑崅偔側傞偲丄僠儍僱儖偑柍偔側傝丄僪儗僀儞揹棳偑慡偔棳傟側偔側傝傑偡丅偙偺尰徾傪乮嬻朢憌偵嫴傑傟偰丄僠儍僱儖偑搑愗傟偰揹棳偑巭傑傞偺偱乯乽僺儞僠丒僆僼乿乮嫴傫偱巭傑傞乯偲屇傃傑偡丅
偙偺傛偆偵俥俤俿偼僎乕僩偵揹埑傪壛偊側偄偲偒嵟戝偺僪儗僀儞揹棳乮俬俢俽俽偲屇偽傟傑偡乯偑棳傟丄僎乕僩偵晧揹埑傪壛偊傞偙偲偱丄僪儗僀儞揹棳偑尭彮偟傑偡丅
壓恾嵍懁偑丄僎乕僩偺揹埑乮僎乕僩僜乕僗娫揹埑乮倁俧俽乯乯偲僪儗僀儞揹棳乮俬俢乯偺娭學偱偡丅倁俧俽偑侽倁偺偲偒丄嵟戝偺俬俢乮俁倣俙掱搙乯偑棳傟丄僎乕僩偵晧偺揹埑傪壛偊傞偲乮僌儔僼偺嵍傊峴偔掱乯俬俢偑尭彮偟丄倁俧俽偑亅侾丏俇倁掱搙偵側傞偲僺儞僠僆僼偟偰偄傑偡丅
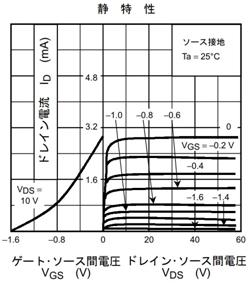
忋恾塃懁偼丄條乆側僎乕僩揹埑倁俧俽偱偺僪儗僀儞僜乕僗娫揹埑倁俢俽偲僪儗僀儞揹棳俬俢偺娭學偱偡丅俥俤俿偵偼僩儔儞僕僗僞偲摨條偵掕揹棳摿惈偑偁傝丄僪儗僀儞揹埑倁俧俽偲偼娭學側偔倁俧俽偱寛傑傞揹棳偑棳傟傞偙偲偑暘偐傝傑偡丅
僩儔儞僕僗僞偼儀乕僗揹棳偱僐儗僋僞揹棳偑寛傑傝丄僐儗僋僞揹棳偼掕揹棳摿惈偑偁傝傑偡丅俥俤俿偼丄僎乕僩揹埑偱僪儗僀儞揹棳偑寛傑傝丄僪儗僀儞揹棳偼掕揹棳摿惈偑偁傝傑偡丅
僩儔儞僕僗僞偺倛俥俤偵偼屄懱嵎偑偁傞傛偆偵丄俥俤俿偺嵟戝僪儗僀儞揹棳俬俢俽俽乮倁俧俽偑侽倁偺帪偺俬俢乯偵傕屄懱嵎偑偁傝傑偡丅偙偺偨傔丄俬俢俽俽偑曄壔偟偰傕塭嬁偺柍偄夞楬傪棙梡偡傞偐丄俥俤俿傪慖暿偟偰棙梡偟傑偡丅
僩儔儞僕僗僞偵俶俹俶偲俹俶俹偑偁傞傛偆偵丄俥俤俿偵偼丄俶僠儍僱儖偲俹僠儍僱儖偑偁傝傑偡丅
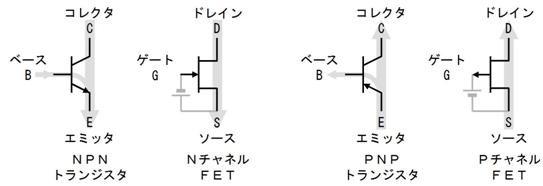
俹僠儍僱儖俥俤俿偼僪儗僀儞偵儅僀僫僗偺揹埑傪妡偗偰揹棳傪棳偟丄僎乕僩偵僾儔僗偺揹埑傪壛偊偰偦偺揹棳傪尭傜偟傑偡丅
俁俉. 俥俤俿傪巊梡偟偨憹暆婍
壓昞偵僩儔儞僕僗僞偺廳梫側惈幙偲懳斾偟偰丄俥俤俿偺廳梫側惈幙傪帵偟傑偡丅
|
捈棳乛岎棳
|
僩儔儞僕僗僞
|
俥俤俿
|
|
捈棳専摙
|
|
|
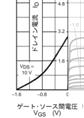
|
|
僄儈僢僞儀乕僗娫揹埑倁俛俤
倁俛俤亖侽丏俈倁
|
僎乕僩僜乕僗娫揹埑倁俧俽
倁俧俽偼俬俢偱曄壔偡傞
|
倁俧俽偲俬俢偼屳偄偵娭學偟偰偄傞偺偱丄倁俧俽亅俬俢僌儔僼偱摦嶌偝偣傞揰傪寛傔傞丅
|
|
僐儗僋僞揹棳俬俠
俬俠亖俬俛亊倛俥俤
|
僪儗僀儞揹棳俬俢
俬俢偼倁俧俽偱曄壔偡傞丅
|
|
俬俠佮俬俤
|
俬俢亖俬俽
|
僩儔儞僕僗僞偲堘偄俥俤俿偱偼僎乕僩偵偼慡偔揹棳偑棳傟側偄偺偱丄俬俢偼姰慡偵俬俽偲摍偟偄丅
|
|
岎棳専摙
|
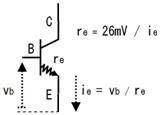
|
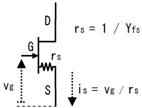
|
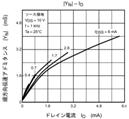
|
|
僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕
倰倕亖俀俇倣倁乛俬俤俤
|
僜乕僗摍壙僀儞僺乕僟儞僗倰倱
倰倱亖侾乛倄倖倱
|
倄倖倱偼俬俢偱曄壔偡傞偺偱丄倄倖倱亅俬俢僌儔僼偱媮傔傞丅乮懡彮偺屄懱嵎傕偁傞乯
|
|
僄儈僢僞怣崋揹棳倝倕
倝倕亖倴倐乛倰倕
|
僜乕僗怣崋揹棳倝倱
倝俽亖倴倗乛倰倱
|
|
僩儔儞僕僗僞偱偼倁俛俤傪栺侽丏俈倁偲寛傔偰専摙偱偒傑偟偨偑丄俥俤俿偱偼倁俧俽偑俬俢偵傛偭偰曄壔偡傞偨傔丄僨乕僞僔乕僩偺僌儔僼偱媮傔傞昁梫偑偁傝傑偡丅
傑偨丄僩儔儞僕僗僞偺倰倕偼倝倕偐傜娙扨偵寁嶼乮俀俇倣倁乛倝倕乯偱偒傑偟偨偑丄俥俤俿偺倰倱偼丄僨乕僞僔乕僩偺僌儔僼偐傜媮傔傞昁梫偑偁傝傑偡丅
偮傑傝丄戝嶨攃側愝寁偱傕僨乕僞僔乕僩偺僌儔僼傪俀偮棙梡偟傑偡丅偙偺偁偨傝偑丄乮棟孅偼戝懱摨偠側偺偱偡偑乯柺搢側強偱丄俥俤俿偵愭棫偭偰僩儔儞僕僗僞傪愢柧偟偨棟桼偱偡丅
壓恾嵍懁偼俥俤俿傪梡偄偨憹暆婍偱丄摨恾塃懁偼俥俤俿乮俀俽俲俁侽乯偺僨乕僞僔乕僩偵宖嵹偝傟偨倁俧俽亅俬俢摿惈恾偱偡丅椺偊偽丄俬俢偑侾丏俇倣俙偱偁傟偽丄倁俧俽偼乕侽丏俆倁偲暘偐傝傑偡丅
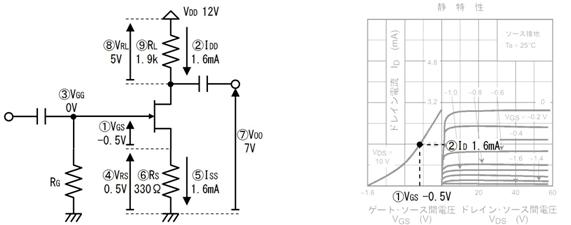
俁俉.侾. 妋擣
忋恾傪嶲峫偵壓昞偵彂偒崬傒側偑傜丄夞楬偺捈棳専摙傪妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
忋恾塃偺倁俧俽亅俬俢僌儔僼偱丄巊梡偡傞揰傪寛傔傑偡丅
偙偙偱偼倁俧俽傪乕侽丏俆倁偱巊梡偡傞偲寛傔傑偡丅
|
亅
|
|
嘇
|
忋恾塃偺僌儔僼傛傝丄僪儗僀儞僶僀傾僗揹棳俬俢俢偼丄
|
倣俙
|
|
嘊
|
僎乕僩偵偼揹棳偑棳傟側偄偐傜丄俼俧偱傾乕僗偵愙懕偝傟偨僎乕僩僶僀傾僗揹埑倁俧俧偼丄
|
倁
|
|
嘋
|
僜乕僗掞峈偺椉抂揹埑倁俼俽偼丄
乮嘊偲嘆偐傜丄乯
|
倁
|
|
嘍
|
僜乕僗僶僀傾僗揹棳俬俽俽偼丄乮俬俢亖俬俽偩偐傜丄乯
|
倣俙
|
|
嘐
|
僜乕僗掞峈俼俽偺抣偼丄
乮嘋偲嘍偐傜丄乯
|
兌
|
|
嘑
|
弌椡僶僀傾僗揹埑倁俷俷傪俈倁偲寛傔傑偡丅
|
亅
|
|
嘒
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
乮倁俠俠偑侾俀倁偩偐傜丄乯
|
倁
|
|
嘓
|
晧壸掞峈俼俴偺抣偼丄
乮嘇偲嘒傛傝丄乯
|
倠兌
|
俁俉.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
忋恾塃偺倁俧俽亅俬俢僌儔僼偱丄巊梡偡傞揰傪寛傔傑偡丅
偙偙偱偼倁俧俽傪乕侽丏俆倁偱巊梡偡傞偲寛傔傑偡丅
|
亅
|
|
嘇
|
忋恾塃偺僌儔僼傛傝丄僪儗僀儞僶僀傾僗揹棳俬俢俢偼丄
|
侾丏俇倣俙
|
|
嘊
|
僎乕僩偵偼揹棳偑棳傟側偄偐傜丄俼俧偱傾乕僗偵愙懕偝傟偨僎乕僩僶僀傾僗揹埑倁俧俧偼丄
|
侽倁
|
|
嘋
|
僜乕僗掞峈偺椉抂揹埑倁俼俽偼丄
乮嘊偲嘆偐傜丄乯
|
侽丏俆倁
|
|
嘍
|
僜乕僗僶僀傾僗揹棳俬俽俽偼丄乮俬俢亖俬俽偩偐傜丄乯
|
侾丏俇倣俙
|
|
嘐
|
僜乕僗掞峈俼俽偺抣偼丄
乮嘋偲嘍偐傜丄乯
|
俁俁侽兌
|
|
嘑
|
弌椡僶僀傾僗揹埑倁俷俷傪俈倁偲寛傔傑偡丅
|
亅
|
|
嘒
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
乮倁俠俠偑侾俀倁偩偐傜丄乯
|
俆倁
|
|
嘓
|
晧壸掞峈俼俴偺抣偼丄
乮嘇偲嘒傛傝丄乯
|
侾丏俋倠兌
|
俁俉.俁. 妋擣
壓恾傪嶲峫偵壓昞偵彂偒崬傒側偑傜丄夞楬偺岎棳専摙傪妋擣偟偰偔偩偝偄丅
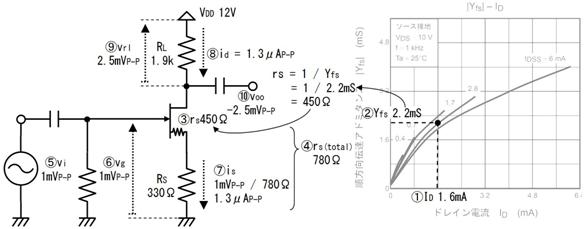
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
捈棳専摙偐傜俬俢偼丄
|
倣俙
|
|
嘇
|
俬俢偼侾丏俇倣俙偱偁傞偐傜丄俬俢亅倄倖倱僌儔僼偐傜丄倄倖倱偺抣偼丄
|
倣俽
|
|
嘊
|
僜乕僗摍壙僀儞僺乕僟儞僗倰倱偺抣偼丄
乮侾乛倄倖倱偩偐傜丄乯
|
兌
|
|
嘋
|
僜乕僗懁偺崌寁僀儞僺乕僟儞僗偼丄
乮倰倱偲俼俽偑捈楍偩偐傜丄乯
|
兌
|
|
嘍
|
擖椡怣崋揹埑倴倝偼丄
|
倣倁俹亅俹
|
|
嘐
|
僎乕僩怣崋揹埑倴倗偼丄
|
倣倁俹亅俹
|
|
嘑
|
僜乕僗怣崋揹棳倝倱偼丄
乮嘋偲嘐偐傜丄乯
|
兪俙俹亅俹
|
|
嘒
|
僪儗僀儞怣崋揹棳倝倓偼丄
乮俬俢亖俬俽偩偐傜丄乯
|
兪俙俹亅俹
|
|
嘓
|
晧壸掞峈偺椉抂怣崋揹埑倴倰倢偼丄
|
倣倁俹亅俹
|
|
嘔
|
弌椡怣崋揹埑倴倧倧偼丄
乮嬌惈偵拲堄偟偰丄乯
|
倣倁俹亅俹
|
|
嘕
|
夞楬偺揹埑憹暆棪偼丄
|
攞
|
俁俉.係. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
捈棳専摙偐傜俬俢偼丄
|
侾丏俇倣俙
|
|
嘇
|
俬俢偼侾丏俇倣俙偱偁傞偐傜丄俬俢亅倄倖倱僌儔僼偐傜丄倄倖倱偺抣偼丄
|
俀丏俀倣俽
|
|
嘊
|
僜乕僗摍壙僀儞僺乕僟儞僗倰倱偺抣偼丄
乮侾乛倄倖倱偩偐傜丄乯
|
係俆侽兌
|
|
嘋
|
僜乕僗懁偺崌寁僀儞僺乕僟儞僗偼丄
乮倰倱偲俼俽偑捈楍偩偐傜丄乯
|
俈俉侽兌
|
|
嘍
|
擖椡怣崋揹埑倴倝偼丄
|
侾倣倁俹亅俹
|
|
嘐
|
僎乕僩怣崋揹埑倴倗偼丄
|
侾倣倁俹亅俹
|
|
嘑
|
僜乕僗怣崋揹棳倝倱偼丄
乮嘋偲嘐偐傜丄乯
|
侾丏俁兪俙俹亅俹
|
|
嘒
|
僪儗僀儞怣崋揹棳倝倓偼丄
乮俬俢亖俬俽偩偐傜丄乯
|
侾丏俁兪俙俹亅俹
|
|
嘓
|
晧壸掞峈偺椉抂怣崋揹埑倴倰倢偼丄
|
俀丏俆倣倁俹亅俹
|
|
嘔
|
弌椡怣崋揹埑倴倧倧偼丄
乮嬌惈偵拲堄偟偰丄乯
|
亅俀丏俆倣倁俹亅俹
|
|
嘕
|
夞楬偺揹埑憹暆棪偼丄
|
亅俀丏俆攞
|
僎乕僩掞峈俼俧偺抣偼丄僎乕僩楻傟揹棳俬俧俽俽偐傜寛傔傑偡丅俀俽俲俁侽偺応崌俬俧俽俽偼侾値俙偱偡偐傜丄俼俧傪侾侽俵兌偲偟偰傕俼俧偺椉抂揹埑偼侾侽倣倁偱夞楬偺摦嶌偵偼塭嬁傪梌偊傑偣傫丅
偙偺傛偆偵丄俥俤俿傪巊梡偟偨憹暆婍偼嬌傔偰崅偄擖椡僀儞僺乕僟儞僗傪摼傞偙偲偑偱偒傑偡偑丄僩儔儞僕僗僞傪巊梡偟偨憹暆婍傛傝傕憹暆棪偑彫偝偔側傞孹岦偑偁傝傑偡丅
俁俋. 俵俷俽俥俤俿
俥俤俿偱偼俹俶愙崌傪嶌偭偰乮媡揹埑傪壛偊偰乯僎乕僩傪愨墢偟偰偄傑偟偨偑丄壓恾偺傛偆偵丄愨墢懱偺敄偄枌傪嶌偭偰僎乕僩傪愨墢偟偨僩儔儞僕僗僞偑俵俷俽俥俤俿偱偡丅
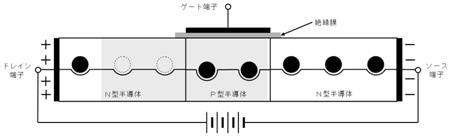
僩儔儞僕僗僞偲帡偨俶俹俶偺愙崌偵椬傝崌偭偰丄愨墢枌偱妘偰偨僎乕僩揹嬌偑愝偗傜傟偰偄傑偡丅僩儔儞僕僗僞偱偼僐儗僋僞偵憡摉偡傞僪儗僀儞偵僾儔僗偺丄僄儈僢僞偵憡摉偡傞僜乕僗偵儅僀僫僗偺揹埑傪壛偊傞偲丄忋恾塃懁偺愙崌柺偼揹棳偑棳傟傑偡偑丄嵍懁偺愙崌柺偼嬻朢憌偑偱偒偰揹棳偑棳傟傑偣傫丅
偙偙偱壓恾忋懁偵帵偡傛偆偵僎乕僩偵僾儔僗偺揹埑傪壛偊傞偲丄偙偺僾儔僗偺揹埑偵堷偐傟偰僎乕僩偺壓偵揹巕偑廤傑傝傑偡丅
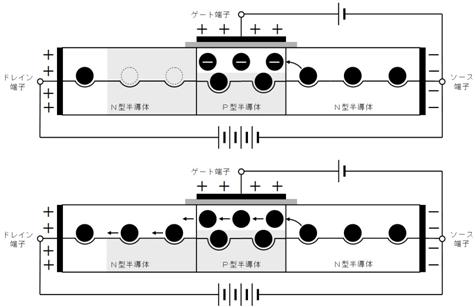
忋恾壓懁偺恾偺帵偡傛偆偵丄僎乕僩偺壓偵廤傑偭偨揹巕偑丄嵍岦偒偵堏摦偡傞偙偲偱僜乕僗偐傜僪儗僀儞偵岦偐偭偰揹巕偑堏摦偱偒傞傛偆偵側傝傑偡丅
暿偺尒曽偱偼丄僎乕僩偺壓偼嵟弶偼俹宆敿摫懱偱偟偨偑丄忋恾偺傛偆偵揹巕偑廤傑偭偨偨傔丄揹巕偑朙晉側俶宆敿摫懱偵曄壔偟偨偲峫偊傑偡丅偙偺傛偆偵嵟弶偺嬌惈乮俹宆乯偲偼媡偺嬌惈乮俶宆乯偵側偭偰偟傑偭偨斖埻傪乽斀揮憌乿偲屇傃傑偡丅斀揮憌偑惗偠偨寢壥丄忋恾壓懁偵帵偡傛偆偵嵍塃偺俶宆椞堟偑斀揮憌傪夘偟偰堦偮偵宷偑傝丄揹棳偑棳傟傞偲偄偆尒曽偱偡丅
俵俷俽俥俤俿偼僎乕僩偵揹埑傪壛偊傞偩偗偱乮揹棳傪棳偟懕偗側偔偰傕乯僪儗僀儞偵揹棳偑棳傟傑偡丅偟偐偟丄僎乕僩偺揹埑傪忋偘傞偨傔偵偼丄僐儞僨儞僒偲摨條偵僎乕僩傪廩揹偡傞昁梫偑偁傝傑偡丅堦斒偵戝揹棳偺俵俷俽俥俤俿偼僎乕僩偺梕検偑戝偒偄偺偱丄廩揹偺偨傔偺揹棳傕戝偒偔側傝傑偡丅
係侽. 俵俷俽俥俤俿偵傛傞僗僀僢僠儞僌夞楬
俵俷俽俥俤俿偼堦扷僎乕僩傪廩揹偡傟偽丄僎乕僩偵揹棳傪棳偟懕偗側偔偰傕戝偒側僪儗僀儞揹棳傪棳偣傞偨傔丄僩儔儞僕僗僞傛傝妝偵戝揹棳傪棳偡偙偲偑偱偒傑偡丅
偨偩偟丄僎乕僩偵壛偊傞揹埑偑晄懌偡傞偲俷俶懝幐乮摫捠懝幐丄揱摫懝幐乯偑敪惗偟丄傑偨丄僎乕僩偺廩曻揹偑抶偄偲僗僀僢僠儞僌懝幐偑敪惗偟偰丄巚傢偸寖偟偄敪擬偑惗偠傞偨傔丄僩儔儞僕僗僞偲偼暿偺拲堄偑昁梫偱偡丅
俵俷俽俥俤俿偑俷俶偟偰丄倁俢俽偑掅偔側偭偨偲偒偺徚旓揹椡乮敪擬乯偑俷俶懝幐偱偡丅倁俢俽偑廫暘偵彫偝偔側傜側偄偨傔偵敪惗偡傞懝幐偱偡丅
壓恾偼俀俽俲俀俀俁俀偺俬俢亅倁俢俽摿惈偱偡丅僪儗僀儞揹棳偼掕揹棳摿惈傪帩偭偰偍傝丄偦偺揹棳偼倁俧俽偱寛傑傝傑偡丅椺偊偽僌儔僼偺嵟傕壓偺嬋慄偑帵偡傛偆偵丄倁俧俽偑俀丏俆倁側傜丄俬俢偼栺俁俙偱偡丅偙偺傛偆側掕揹棳忬懺偱俵俷俽俥俤俿傪巊梡偡傞偲丄倁俢俽偑戝偒偄偨傔敪擬傕戝偒偔側傝傑偡丅捠忢俵俷俽俥俤俿偼偙偺傛偆側掕揹棳忬懺偱偼巊梡偟傑偣傫丅
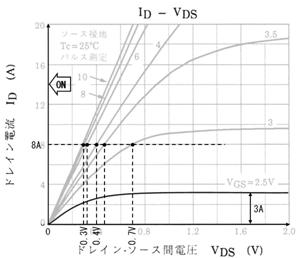
捠忢丄俵俷俽俥俤俿偼俷俶偵偟偰乮倁俢俽傪侽倁偵嬤晅偗偰乯俬俢傪棳偟偰巊梡偟傑偡丅偦偙偱忋恾僌儔僼偱俬俢偑俉俙偺応崌偺倁俢俽偵拲栚偡傞偲丄倁俧俽偑俁倁側傜倁俢俽偼侽丏俈倁丄係倁側傜侽丏係倁丄俉倁側傜侽丏俁倁偲丄倁俧俽偑戝偒偔側傞偲倁俢俽偑彫偝偔側傝傑偡丅
偮傑傝丄俵俷俽俥俤俿傪廫暘偵俷俶偵偡傞乮倁俢俽傪廫暘偵彫偝偔偡傞乯偨傔偵偼丄倁俧俽傪偁傞掱搙崅偔偡傞昁梫偑偁傝傑偡丅媡偵倁俧俽偑掅偄偲僪儗僀儞偵揹棳偼棳傟傞傕偺偺丄倁俢俽偑戝偒偔敪擬偑戝偒偔側傝傑偡丅
俵俷俽俥俤俿傪廫暘偵俷俶偱偒傞倁俧俽偼昳庬偵傛偭偰堎側傝傑偡丅掅偄倁俧俽偱傕廫暘偵俷俶偵側傞傛偆偵愝寁偝傟偨昳庬傕偁傝丄僨乕僞僔乕僩偵乽掅揹埑嬱摦乿乽係倁嬱摦乿乽掅揹埑僎乕僩僪儔僀僽壜擻乿摍偲婰嵹偝傟偰偄傑偡丅
壓恾偼俀俽俲係侽侾俈乮係倁嬱摦壜擻乯偺俬俢亅倁俢俽摿惈偱丄倁俧俽偑係倁偁傟偽丄悢俙偺揹棳傪棳偟偰傕倁俢俽偑偐側傝掅偔側傞乮俷俶偵側傞乯偙偲偑暘偐傝傑偡丅
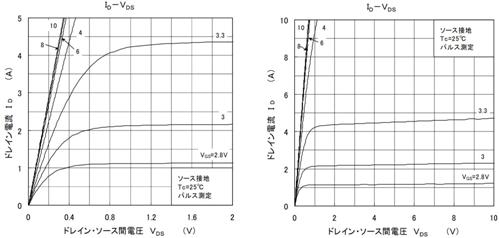
係侾.侾. 楙廗
壓恾偼俁倁偱摦嶌偡傞俠俵俷俽儘僕僢僋偱俀俽俲係侽侾俈偺僎乕僩傪捈愙嬱摦偟偨夞楬偱偡丅忋恾偺僌儔僼傪巊梡偟偰丄壓恾偺夞楬偑俷俶偟偰偄傞偲偒偺俵俷俽俥俤俿偺徚旓揹椡俹俢傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
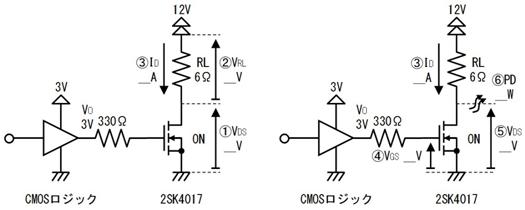
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俵俷俽俥俤俿偑俷俶偟偰偄傞偲偒丄倁俢俽偼丄
|
倁
|
|
嘇
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
倁
|
|
嘊
|
僪儗僀儞揹棳俬俢偼丄
|
俙
|
|
嘋
|
倁俧俽偼丄
乮俠俷俵俽儘僕僢僋偺弌椡偑俁倁偩偐傜丄乯
|
倁
|
|
嘍
|
忋偺僌儔僼偐傜丄嘋偺倁俧俽偱丄嘊偺俬俢偺応崌偺丄僪儗僀儞僜乕僗娫揹埑倁俢俽偼丄
|
倁
|
|
嘐
|
俵俷俽俥俤俿偺徚旓揹椡俹俢偼丄乮嘊偲嘍偐傜丄乯
乮嘍偺倁俢俽偑倁俼俴傗俬俢偵梌偊傞塭嬁傪柍帇偟偰丄乯
|
倂
|
|
嘑
|
僷僢働乕僕偺乮曻擬婍側偟偺乯擬掞峈傪侾俀俆亷乛倂偲偡傞偲丄僠僢僾偺壏搙忋徃偼丄
乮壏搙忋徃亖徚旓揹椡亊擬掞峈丂偩偐傜丄乯
|
亷
|
|
嘒
|
婥壏偑係侽亷偺偲偒丄僠僢僾偺壏搙偼丄
乮僠僢僾壏搙亖婥壏亄壏搙忋徃丂偩偐傜丄乯
|
亷
|
係侾.俀. 摎
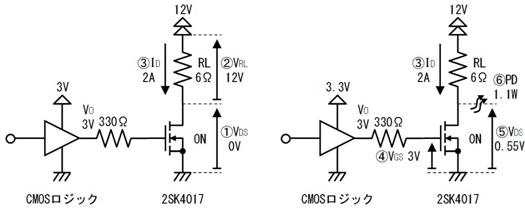
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俵俷俽俥俤俿偑俷俶偟偰偄傞偲偒丄倁俢俽偼丄
|
侽倁
|
|
嘇
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
侾俀倁
|
|
嘊
|
僪儗僀儞揹棳俬俢偼丄
|
俀俙
|
|
嘋
|
倁俧俽偼丄
乮俠俷俵俽儘僕僢僋偺弌椡偑俁倁偩偐傜丄乯
|
俁倁
|
|
嘍
|
忋偺僌儔僼偐傜丄嘋偺倁俧俽偱丄嘊偺俬俢偺応崌偺丄僪儗僀儞僜乕僗娫揹埑倁俢俽偼丄
|
侽丏俆俆倁
|
|
嘐
|
俵俷俽俥俤俿偺徚旓揹椡俹俢偼丄乮嘊偲嘍偐傜丄乯
乮嘍偺倁俢俽偑倁俼俴傗俬俢偵梌偊傞塭嬁傪柍帇偟偰丄乯
侽丏俀俆倁亊俀俙亖侽丏俆倂
|
侾丏侾倂
|
|
嘑
|
僷僢働乕僕偺乮曻擬婍側偟偺乯擬掞峈傪侾俀俆亷乛倂偲偡傞偲丄僠僢僾偺壏搙忋徃偼丄
壏搙忋徃亖徚旓揹椡亊擬掞峈
丂丂丂丂亖侾丏侾倂亊侾俀俆亷乛倂亖侾俁俉亷
|
侾俁俉亷
|
|
嘒
|
婥壏偑係侽亷偺偲偒丄僠僢僾偺壏搙偼丄
僠僢僾壏搙亖婥壏亄壏搙忋徃
丂丂丂丂丂亖係侽亷亄侾俁俉亷亖侾俈俉亷
|
侾俈俉亷
|
偙偺傛偆偵丄係倁嬱摦壜擻側俵俷俽俥俤俿傪俁倁偱嬱摦偡傞偲丄倁俢俽偑戝偒偔側傝丄偙偺椺偱偼侾丏侾倂偺揹椡偑徚旓偝傟丄曻擬婍傪晅偗側偗傟偽僠僢僾偼侾俈俉亷偲側傝乮侾俆侽亷偱夡傟傑偡偐傜乯慺巕偼擬偱攋夡偟傑偡丅
係侾.俁. 楙廗
壓恾偼婛偵楙廗偟偨夞楬偺嬱摦揹埑傪俁倁偐傜俆倁偵崅傔偨夞楬偱偡丅婛弌偺僌儔僼傪巊梡偟偰丄壓恾偺夞楬偑俷俶偟偰偄傞偲偒偺俵俷俽俥俤俿偺徚旓揹椡俹俢傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
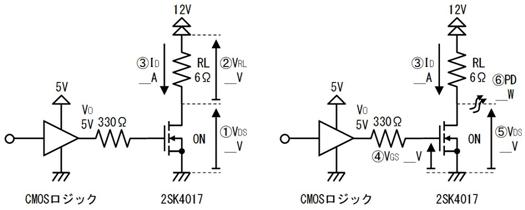
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俵俷俽俥俤俿偑俷俶偟偰偄傞偲偒丄倁俢俽偼丄
|
倁
|
|
嘇
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
倁
|
|
嘊
|
僪儗僀儞揹棳俬俢偼丄
|
俙
|
|
嘋
|
倁俧俽偼丄
乮俠俷俵俽儘僕僢僋偺弌椡偑俆倁偩偐傜丄乯
|
倁
|
|
嘍
|
忋偺僌儔僼偐傜丄嘋偺倁俧俽偱丄嘊偺俬俢偺応崌偺丄僪儗僀儞僜乕僗娫揹埑倁俢俽偼丄
|
倁
|
|
嘐
|
俵俷俽俥俤俿偺徚旓揹椡俹俢偼丄乮嘊偲嘍偐傜丄乯
乮嘍偺倁俢俽偑倁俼俴傗俬俢偵梌偊傞塭嬁傪柍帇偟偰丄乯
|
倂
|
|
嘑
|
僷僢働乕僕偺乮曻擬婍側偟偺乯擬掞峈傪侾俀俆亷乛倂偲偡傞偲丄僠僢僾偺壏搙忋徃偼丄
壏搙忋徃亖徚旓揹椡亊擬掞峈
|
亷
|
|
嘒
|
婥壏偑係侽亷偺偲偒丄僠僢僾偺壏搙偼丄
僠僢僾壏搙亖婥壏亄壏搙忋徃
|
亷
|
係侾.係. 摎
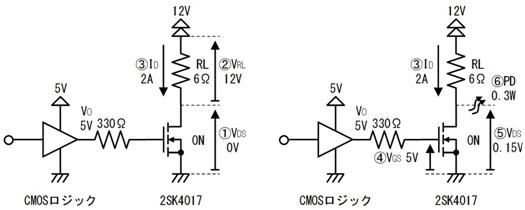
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俵俷俽俥俤俿偑俷俶偟偰偄傞偲偒丄倁俢俽偼丄
|
侽倁
|
|
嘇
|
晧壸掞峈偺椉抂揹埑倁俼俴偼丄
|
侾俀倁
|
|
嘊
|
僪儗僀儞揹棳俬俢偼丄
|
俀俙
|
|
嘋
|
倁俧俽偼丄
乮俠俷俵俽儘僕僢僋偺弌椡偑俆倁偩偐傜丄乯
|
俆倁
|
|
嘍
|
忋偺僌儔僼偐傜丄嘋偺倁俧俽偱丄嘊偺俬俢偺応崌偺丄僪儗僀儞僜乕僗娫揹埑倁俢俽偼丄
|
侽丏侾俆倁
|
|
嘐
|
俵俷俽俥俤俿偺徚旓揹椡俹俢偼丄乮嘊偲嘍偐傜丄乯
乮嘍偺倁俢俽偑倁俼俴傗俬俢偵梌偊傞塭嬁傪柍帇偟偰丄乯
侽丏俀俆倁亊俀俙亖侽丏俆倂
|
侽丏俁倂
|
|
嘑
|
僷僢働乕僕偺乮曻擬婍側偟偺乯擬掞峈傪侾俀俆亷乛倂偲偡傞偲丄僠僢僾偺壏搙忋徃偼丄
壏搙忋徃亖徚旓揹椡亊擬掞峈
丂丂丂丂亖侽丏俁倂亊侾俀俆亷乛倂亖俈俆亷
|
俈俆亷
|
|
嘒
|
婥壏偑係侽亷偺偲偒丄僠僢僾偺壏搙偼丄
僠僢僾壏搙亖婥壏亄壏搙忋徃
丂丂丂丂丂亖係侽亷亄俈俆亷亖侾侾俆亷
|
侾侾俆亷
|
俆倁偱嬱摦偡傞偙偲偱倁俢俽偑侽丏侾俆倁偵掅偔側傝丄敪擬偼俁侽侽倣倂偵丄僠僢僾壏搙偼侾侾俆亷偵壓偑傝傑偡丅僠僢僾壏搙偑崅偔庻柦偺抁弅傕偁傝傑偡偑丄懄嵗偵夡傟傞偙偲偼柍偔側傝傑偡丅彫偝側曻擬婍傪晅偗傟偽僠僢僾壏搙偑壓偑傝丄幚梡弌棃傑偡丅
崅偄揹埑偱巊梡偱偒傞俵俷俽俥俤俿乮倁俢俽偺嵟戝抣偺戝偒側昳庬偺乯偼丄俷俶帪偺倁俢俽偑戝偒偔側傞孹岦偑偁傝傑偡丅廬偭偰丄柍埮偵倁俢俽偺嵟戝抣偺戝偒側昳庬傪巊傢側偄曽偑丄俷俶懝幐傪尭傜偡偙偲偑偱偒傑偡丅
俵俷俽俥俤俿偼俷俶帪偩偗偱偼側偔丄壓恾偵嵍塃曽岦偺栴報偱帵偡丄俷俥俥偐傜俷俶偵曄壔偡傞弖娫偲丄俷俶偐傜俷俥俥偵曄壔偡傞弖娫偵傕敪擬偟傑偡丅偙偺敪擬傪僗僀僢僠儞僌懝幐偲屇傃傑偡丅
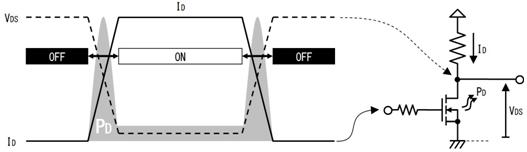
俵俷俽俥俤俿偺懝幐俹俢傪丄忋恾偵奃怓偱帵偟傑偡丅倁俢俽偑揹尮揹埑偺敿暘偵側偭偨偲偒丄嵟戝偺揹椡偑徚旓偝傟傞偨傔丄忋恾拞偺俀偮偺嶳偑僗僀僢僠儞僌懝幐傪帵偟傑偡丅嶳偲嶳偺娫偺暯傜側奃怓偺晹暘偼丄偡偱偵楙廗偟偨俷俶懝幐乮摫捠懝幐乯偵傛傞敪擬偱偡丅
壓恾乮倎乯偺傛偆偵丄僗僀僢僠儞僌偑備偭偔傝偱偁傞偲丄嶳偺墶暆偑峀偑偭偰僗僀僢僠儞僌懝幐偑憹壛偟傑偡丅傑偨丄壓恾乮倐乯偺傛偆偵丄僗僀僢僠儞僌偺昿搙偑崅偔偰傕丄僗僀僢僠儞僌懝幐偑憹壛偟傑偡丅
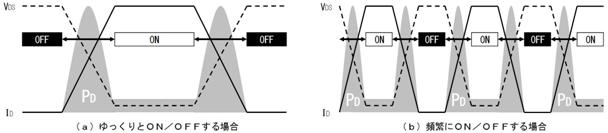
偱偡偐傜丄僗僀僢僠儞僌傪慺憗偔峴偄丄僗僀僢僠儞僌昿搙傪揔搙偵梷偊傞偙偲偱僗僀僢僠儞僌懝幐傪彫偝偔偟傑偡丅
壓恾偵俵俷俽俥俤俿偺俷俶乛俷俥俥帪偺僎乕僩揹埑倁俧俽乮幚慄乯偲丄僪儗僀儞揹埑倁俢俽乮揰慄乯傪帵偟傑偡丅
俵俷俽俥俤俿傪俷俶偵偡傞偲偒偼丄僎乕僩傪廩揹偟傑偡丅俵俷俽俥俤俿偺僎乕僩偵偼戝偒側梕検偑偁傞偺偱丄僎乕僩偵揹棳傪棳偡偲俠俬俽俽偑廩揹偝傟偰丄嘆揹埑偑忋徃傪巒傔傑偡丅僎乕僩偺揹埑偑忋徃偟偰丄僪儗僀儞揹棳俬俢偑憹偊巒傔傞偲丄倁俢俽偑掅壓傪巒傔丄俠俼俽俽傪夘偟偰乮忋偑傠偆偲偟偰偄傞乯僎乕僩偺揹埑傪堷偒壓偘傞乮僩儔儞僕僗僞偲摨條乽儈儔乕岠壥乿偲屇傃傑偡乯偨傔丄嘇僎乕僩偺揹埑偼忋徃傪巭傔傑偡丅俵俷俽俥俤俿偑俷俶偵側傝倁俢俽偺掅壓偑巭傑傞偲丄儈儔乕岠壥側偔側傝丄俠俬俽俽偺廩揹偑嵞奐偝傟偰嘊僎乕僩揹埑偑嵞傃忋徃傪巒傔傑偡丅
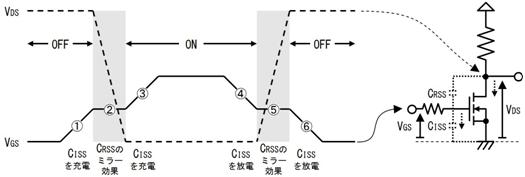
傑偨丄俵俷俽俥俤俿傪俷俥俥偵偡傞偲偒偼丄僎乕僩傪曻揹偟傑偡丅僎乕僩偐傜揹棳傪媧偄弌偡偲丄俠俬俽俽偑曻揹偝傟偰丄嘋揹埑偑掅壓傪巒傔傑偡丅僎乕僩偺揹埑偑掅壓偟偰丄僪儗僀儞揹棳俬俢偑尭傝巒傔傞偲丄倁俢俽偑忋徃傪巒傔丄俠俼俽俽傪夘偟偰乮壓偑傠偆偲偟偰偄傞乯僎乕僩偺揹埑傪堷偒忋偘傞偘傞乮僩儔儞僕僗僞偲摨條乽儈儔乕岠壥乿偲屇傃傑偡乯偨傔丄嘍僎乕僩偺揹埑偼掅壓傪巭傔傑偡丅俵俷俽俥俤俿偑俷俥俥偵側傝倁俢俽偺忋徃偑巭傑傞偲丄儈儔乕岠壥側偔側傝丄俠俬俽俽偺曻揹偑嵞奐偝傟偰嘐僎乕僩揹埑偑嵞傃掅壓傪巒傔傑偡丅
僗僀僢僠儞僌傪慺憗偔峴偆偨傔偵偼丄戝偒側揹棳偱僎乕僩傪廩曻揹偟偰丄嘆嘇嘊嘋嘍嘐偺帪娫丄偲傝傢偗嘇嘍偺帪娫傪抁偔偡傞昁梫偑偁傝傑偡丅
壓恾偼僐儞僾儕儊儞僞儕僄儈僢僞僼僅儘傾傪棙梡偟偰慺憗偔僎乕僩傪廩曻揹偡傞夞楬偱偡丅僎乕僩偺弌椡偑俫偺応崌偼丄壓恾乮倎乯偵帵偡傛偆偵忋懁偺僩儔儞僕僗僞偑揹棳傪棳偟偰倛俥俤攞偺揹棳偱僎乕僩傪廩揹偟傑偡丅傑偨丄僎乕僩偺弌椡偑俴偺応崌偼丄壓恾乮倐乯偵帵偡傛偆偵壓懁偺僩儔儞僕僗僞偑揹棳傪棳偟偰倛俥俤攞偺揹棳偱僎乕僩傪曻揹偟傑偡丅
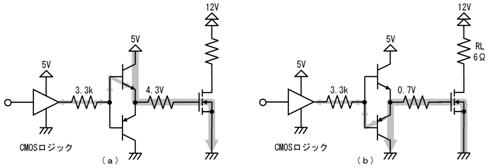
忋恾偺夞楬偺寚揰偼僩儔儞僕僗僞偺倁俛俤偺塭嬁偱丄俷俶帪偺倁俧俽偑係丏俁倁傑偱偟偐忋徃偟側偄偙偲偱偡丅偙偺塭嬁偱丄俷俶帪偺倁俢俽偑戝偒偔側傝丄俷俶懝幐偑戝偒偔側傞応崌偑偁傝傑偡丅
壓恾偺夞楬偼崅偄倁俧俽傪壛偊偰俷俶懝幐傪尭傜偟丄偐偮戝揹棳偱慺憗偔僎乕僩偺廩曻揹傪峴偄僗僀僢僠儞僌懝幐傪尭傜偡夞楬偱偡丅
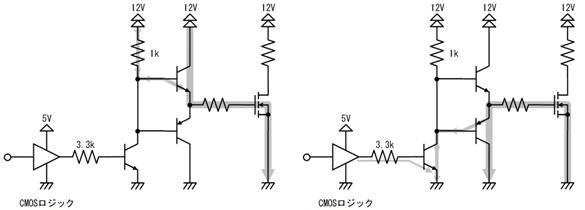
壓恾偺傛偆偵儘乕僒僀僪僪儔僀僶俬俠傪巊梡偡傞偲丄娙扨側夞楬偱慺憗偔僎乕僩傪俷俶乛俷俥俥偱偒傑偡丅
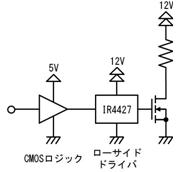
桿摫晧壸乮僐僀儖惉暘偺偁傞晧壸乯傪俷俶乛俷俥俥偡傞応崌偼丄俵俷俽俥俤俿傕僩儔儞僕僗僞偲摨條偵僗僫僶夞楬傪庢傝晅偗傑偡丅
俵俷俽俥俤俿偺僪儗僀儞僜乕僗娫偵偼僣僃乕僫僟僀僆乕僪偵帡偨惈幙偑偁傝丄偙偺惈幙傪棙梡偟偰僼儔僀僶僢僋揹埑傪梷偊傜傟傞昳庬傕偁傝傑偡丅
壓昞偼俀俽俲係侽侾俈偺僨乕僞僔乕僩偺堦晹偱偡偑丄僪儗僀儞僜乕僗娫崀暁揹埑乮倁俛俼乯偼乮倁俧俽偑侽倁偺応崌乯俇侽倁偲婰嵹偝傟偰偄傑偡丅偮傑傝丄僼儔僀僶僢僋揹埑偼俇侽倁偱梷惂偝傟傑偡丅
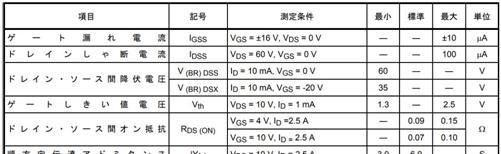
偨偩偟丄偁傑傝戝偒側揹棳傪媧廂偝偣傞偲俵俷俽俥俤俿偑攋懝偟傑偡丅壓恾偺愨懳嵟戝掕奿偵傛傟偽丄傾僶儔儞僔僃揹棳偼俆俙偱丄傾僶儔儞僔僃僄僱儖僊乕偼俀倣俰偱偡丅
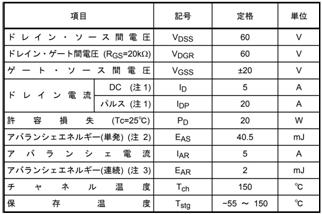
僼儔僀僶僢僋揹棳偼晧壸偺嵟戝揹棳偲傎傏摍偟偔側傝傑偡偐傜丄嵟戝揹棳傪俆俙傛傝廫暘彫偝偔偡傞昁梫偑偁傝傑偡丅
傾僶儔儞僔僃僄僱儖僊偼丄
傾僶儔儞僔僃揹棳
亊 僪儗僀儞僜乕僗娫崀暁揹埑
亊 揹棳偺棳傟傞帪娫 亐 俀
偱媮傔傑偡丅乮俀偱妱傞棟桼偼丄揹棳攇宍偑嶰妏宍偵側傞偨傔丄嶰妏宍偺柺愊偱僄僱儖僊傪媮傔傞偐傜偱偡丅乯
椺偊偽丄俀俙偱俇侽倁偺僼儔僀僶僢僋偑俆兪昩棳傟傞応崌偼丄=2*60*5E-6/2偲寁嶼偟偰丄侽丏俁倣俰偲媮傔傞偙偲偑偱偒傑偡丅
侾. 揹棳僽乕僗僞
僆儁傾儞僾偵僄儈僢僞僼僅儘傾傪捛壛偡傞帠偱丄弌椡揹棳傪戝偒偔偡傞偙偲偑偱偒傑偡丅弌椡揹棳傪憹嫮乮僽乕僗僩乯偡傞偺偱丄揹棳僽乕僗僞偲屇偽傟傑偡丅
椺偊偽丄俿俢俙俀侽俁侽乮僆乕僨傿僆僷儚乕傾儞僾偲屇偽傟偰傑偡偑丄幚偼俁俙俀侽倂偺僷儚乕僆儁傾儞僾偱偡乯偺傛偆偵戝偒側揹棳傪弌椡偱偒傞僆儁傾儞僾傕埨壙偵側偭偰偄傞偨傔丄僆儁傾儞僾偺弌椡揹棳傪憹嫮偡傞夞楬偼埲慜傎偳廳梫偱偼偁傝傑偣傫丅
偲偼偄偊丄庤帩偪偺僆儁傾儞僾偲僩儔儞僕僗僞偱丄庤寉偵弌椡揹棳傪憹傗偡偙偲偑偱偒傟偽曋棙偱偡偐傜丄偙偙偱偼揹棳僽乕僗僞偵偮偄偰愢柧偟傑偡丅
揹棳傪揻偒弌偡偐丄媧偄弌偡偐丄偄偢傟偐堦曽偩偗偺摦嶌傪偡傞夞楬傪僔儞僌儖僽乕僗僞偲屇傃傑偡丅
偝偰丄壓恾乮倎乯偼僆儁傾儞僾傪棙梡偟偨侾侽攞偺旕斀揮憹暆夞楬偱偡丅壓恾乮倐乯偺傛偆偵丄偙偺夞楬偵僄儈僢僞僼僅儘傾傪捛壛偡傞偲丄弌椡揹棳傪戝偒偔偡傞偙偲偑偱偒傑偡丅偙偺夞楬偼丄揹棳傪揻偒弌偡偙偲偼偱偒傑偡偑丄媧偄崬傓偙偲偼偱偒傑偣傫丅
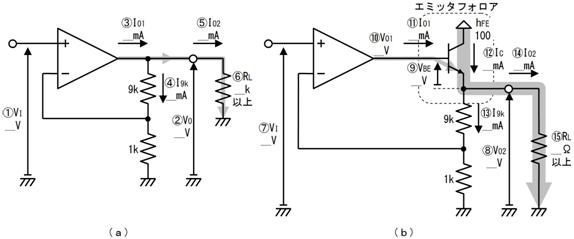
俀.侾. 妋擣
忋恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜夞楬偺摦嶌傪妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
|
忋恾乮倎乯偱丄僆儁傾儞僾偩偗偺旕斀揮憹暆夞楬偵偮偄偰峫偊傑偡丅
|
|
|
嘆
|
擖椡揹埑倁俬偼丄
|
倁
|
|
嘇
|
弌椡揹埑倁俷偼丄
|
倁
|
|
嘊
|
偙偺僆儁傾儞僾偼俀倣俙傑偱偺揹棳傪弌椡偱偒傞偲偟傑偡丅
|
俀倣俙
|
|
嘋
|
俋倠兌偵棳傟傞揹棳俬俋倠偼丄
乮擖椡偵揹棳偑棳傟偢丄俋倠偲侾倠偱侾侽倠偩偐傜丄乯
|
倣俙
|
|
嘍
|
奜晹偵弌椡偱偒傞揹棳俬俷俀偼丄
乮嘊偲嘋偐傜僉儖僸懃偱丄乯
|
倣俙
|
|
嘐
|
晧壸掞峈俼俴偺嵟掅抣偼丄
乮嘇偲嘍偐傜丄乯
|
倠兌埲忋
|
|
|
忋恾乮倐乯偱丄僄儈僢僞僼僅儘傾傪捛壛偟偨斀揮憹暆夞楬偵偮偄偰峫偊傑偡丅
|
|
|
嘑
|
擖椡揹埑倁俬偼丄
|
倁
|
|
嘒
|
弌椡揹埑倁俷俀偼丄
|
倁
|
|
嘓
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘔
|
僆儁傾儞僾偺弌椡抂巕偺倁俷侾偼丄
|
倁
|
|
嘕
|
偙偺僆儁傾儞僾偼俀倣俙傑偱偺揹棳傪弌椡偱偒傞偲偟傑偡丅
|
俀倣俙
|
|
嘖
|
僐儗僋僞揹棳俬俠偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
倣俙
|
|
嘗
|
俋倠兌偵棳傟傞揹棳俬俋倠偼丄
|
倣俙
|
|
嘙
|
奜晹偵弌椡偱偒傞揹棳俬俷俀偼丄
乮嘖偲嘗偐傜僉儖僸懃偱丄乯
|
倣俙
|
|
嘚
|
晧壸掞峈俼俴偺嵟掅抣偼丄
乮嘒偲嘙偐傜丄乯
|
兌埲忋
|
俀.俀. 摎
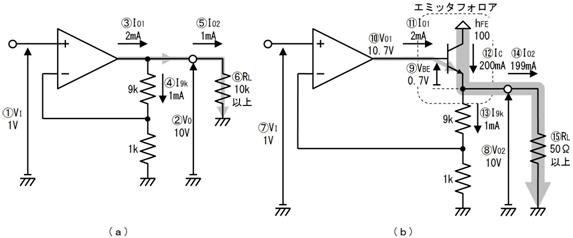
|
斣崋
|
幙栤
|
抣
|
|
|
忋恾乮倎乯偱丄僆儁傾儞僾偩偗偺旕斀揮憹暆夞楬偵偮偄偰峫偊傑偡丅
|
|
|
嘆
|
擖椡揹埑倁俬偼丄
|
侾倁
|
|
嘇
|
弌椡揹埑倁俷偼丄
|
侾侽倁
|
|
嘊
|
偙偺僆儁傾儞僾偼俀倣俙傑偱偺揹棳傪弌椡偱偒傞偲偟傑偡丅
|
俀倣俙
|
|
嘋
|
俋倠兌偵棳傟傞揹棳俬俋倠偼丄
乮擖椡偵揹棳偑棳傟偢丄俋倠偲侾倠偱侾侽倠偩偐傜丄乯
|
侾倣俙
|
|
嘍
|
奜晹偵弌椡偱偒傞揹棳俬俷俀偼丄
乮嘊偲嘋偐傜僉儖僸懃偱丄乯
|
侾倣俙
|
|
嘐
|
晧壸掞峈俼俴偺嵟掅抣偼丄
乮嘇偲嘍偐傜丄乯
|
侾侽倠兌埲忋
|
|
|
忋恾乮倐乯偱丄僄儈僢僞僼僅儘傾傪捛壛偟偨斀揮憹暆夞楬偵偮偄偰峫偊傑偡丅
|
|
|
嘑
|
擖椡揹埑倁俬偼丄
|
侾倁
|
|
嘒
|
弌椡揹埑倁俷俀偼丄
|
侾侽倁
|
|
嘓
|
揹棳偑棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘔
|
僆儁傾儞僾偺弌椡抂巕偺倁俷侾偼丄
|
侾侽丏俈倁
|
|
嘕
|
偙偺僆儁傾儞僾偼俀倣俙傑偱偺揹棳傪弌椡偱偒傞偲偟傑偡丅
|
俀倣俙
|
|
嘖
|
僐儗僋僞揹棳俬俠偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
俀侽侽倣俙
|
|
嘗
|
俋倠兌偵棳傟傞揹棳俬俋倠偼丄
|
侾倣俙
|
|
嘙
|
奜晹偵弌椡偱偒傞揹棳俬俷俀偼丄
乮嘖偲嘗偐傜僉儖僸懃偱丄乯
|
侾俋俋倣俙
|
|
嘚
|
晧壸掞峈俼俴偺嵟掅抣偼丄
乮嘒偲嘙偐傜丄乯
|
俆侽兌埲忋
|
偙偺傛偆偵僄儈僢僞僼僅儘傾傪捛壛偡傞偙偲偱丄弌椡揹棳傪奣偹倛俥俤攞偵奼戝偱偒傑偡丅乮忋昞嘙乯偦偺寢壥丄僆儁傾儞僾扨懱偱偼侾侽倠兌傑偱偺晧壸偟偐愙懕偱偒傑偣傫偱偟偨偑乮忋昞嘐乯丄僄儈僢僞僼僅儘傾傪捛壛偡傞偲俆侽兌傑偱偺晧壸傪愙懕偱偒傑偡乮忋昞嘚乯丅
偝傜偵丄僄儈僢僞僼僅儘傾偱惗偠傞丄擖弌椡偺揹埑嵎乮侽丏俈倁乯傪僆儁傾儞僾偑媧廂偟偰丄惓妋偵擖椡揹埑傪憹暆偟偨揹埑偑弌椡偝傟傑偡丅乮忋昞嘒嘓嘔乯偨偩偟丄弌椡偱偒傞嵟崅偺揹埑偼丄侽丏俈倁乮倁俛俤偺暘乯掅偔側傝傑偡丅
俀.俁. 楙廗
壓恾偼丄嵟戝俀俆侽倣俙傪弌椡偱偒傞揹棳僽乕僗僞偱偡丅巊梡偟偰偄傞僆儁傾儞僾偼丄嵟崅侾俁丏俆倁傪弌椡偱偒傑偡丅偙偺夞楬偑弌椡偱偒傞揹埑偺嵟戝抣傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
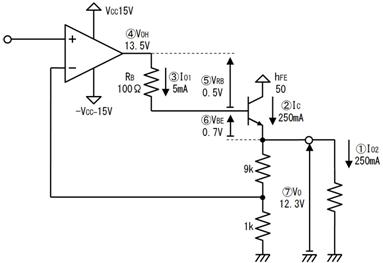
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
夞楬偺嵟戝弌椡揹棳偼俀俆侽倣俙偱偡丅
|
亅
|
|
嘇
|
僐儗僋僞揹棳俬俠偼丄
|
倣俙
|
|
嘊
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑俆侽偩偐傜丄乯
|
倣俙
|
|
嘋
|
僆儁傾儞僾偺嵟戝弌椡揹埑偼侾俁丏俆倁偱偡丅
|
亅
|
|
嘍
|
儀乕僗掞峈偺椉抂揹埑倁俼俛偼丄
|
倁
|
|
嘐
|
倁俛俤偼丄
|
倁
|
|
嘑
|
弌椡揹埑偼丄
|
倁
|
俀.係. 摎
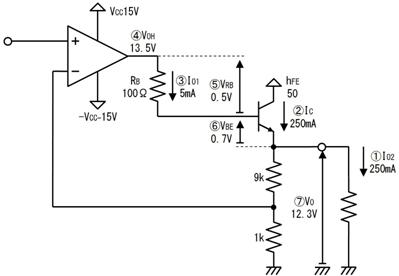
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
夞楬偺嵟戝弌椡揹棳偼俀俆侽倣俙偱偡丅
|
亅
|
|
嘇
|
僐儗僋僞揹棳俬俠偼丄
|
俀俆侽倣俙
|
|
嘊
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤偑俆侽偩偐傜丄乯
|
俆倣俙
|
|
嘋
|
僆儁傾儞僾偺嵟戝弌椡揹埑偼侾俁丏俆倁偱偡丅
|
亅
|
|
嘍
|
儀乕僗掞峈偺椉抂揹埑倁俼俛偼丄
|
侽丏俆倁
|
|
嘐
|
倁俛俤偼丄
|
侽丏俈倁
|
|
嘑
|
弌椡揹埑偼丄
|
侾俀丏俁倁
|
偙偺傛偆偵俼俛傪捛壛偡傞偲丄嵟崅弌椡揹埑偑掅偔側傝傑偡丅俼俛偼僆儁傾儞僾偺弌椡傪曐岇偟丄傑偨丄崅偄廃攇悢偱偺僆儁傾儞僾傗僩儔儞僕僗僞偺摦嶌傪埨掕偝偣傞偨傔偵憓擖偟偰偄傑偡丅揹尮揹埑偑俆倁掱搙側傜昁梫偁傝傑偣傫偑丄揹尮揹埑偑崅偄応崌偼昁梫偱偡丅
壓恾偺傛偆偵丄僆儁傾儞僾偵僐儞僾儕儊儞僞儕僄儈僢僞僼僅儘傾傪捛壛偡傞偙偲傕偱偒傑偡丅弌椡揹棳傪戝偒偔偱偒傞偩偗偱偼側偔丄壓恾偺嵍塃偵帵偡傛偆偵丄揹棳傪媧偄崬傓偙偲傕丄揻偒弌偡偙偲傕偱偒傑偡丅
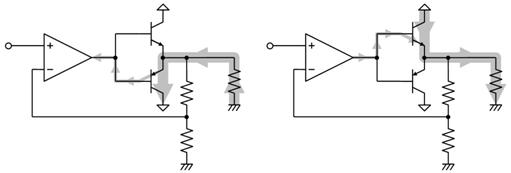
扨弮側僐儞僾儕儊儞僞儕僄儈僢僞僼僅儘傾偼丄壓恾乮倎乯偵帵偡傛偆偵丄僋儘僗僆乕僶乕榗傒傪敪惗偟傑偡丅
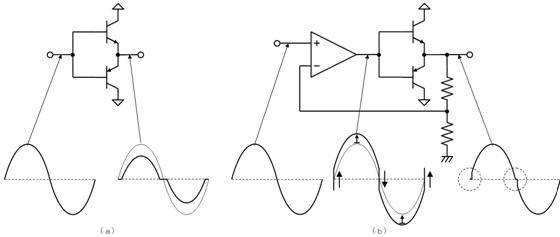
偟偐偟丄僄儈僢僞僼僅儘傾傪僆儁傾儞僾偲慻傒崌傢偣傞偙偲偱丄忋恾乮倐乯偺拞墰偺攇宍偵帵偡傛偆偵丄僆儁傾儞僾偑倁俛俤偺揹埑傪曗偭偰摦嶌偟丄忋晹乮倐乯偺塃懁偺攇宍偵帵偡傛偆偵丄僋儘僗僆乕僶乕榗傒傪彫偝偔偡傞偙偲偑偱偒傑偡丅
偙偺偲偒丄忋恾乮倐乯偵栴報偱帵偡傛偆偵丄僆儁傾儞僾偼亅侽丏俈倁乣亄侽丏俈倁傑偱堦弖偱棫偪忋偑傞乮棫偪壓偑傞乯昁梫偑偁傝傑偡丅偟偐偟丄尰幚偵偼乽堦弖乿偲偼峴偐側偄偨傔丄偙偙偱僆儁傾儞僾偺摦嶌偑屻傟偨暘偑榗傒偵側傝傑偡丅
偙偺夞楬偼儌乕僟摍傪嬱摦偡傞側傜廫暘側惈擻偱偡偑丄椙岲側壒幙偱僗僺乕僇乕傪柭傜偡偵偼椡晄懌偱偡丅
俁.侾. 楙廗
壓恾偺僐儞僾儕儊儞僞儕揹棳僽乕僗僞夞楬偺奺晹偺揹埑丒揹棳傪丄壓昞偵彂偒崬傒側偑傜専摙偟偰偔偩偝偄丅
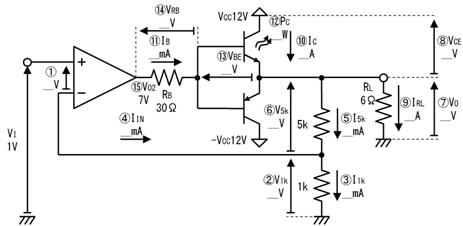
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
晧婣娨偑妡偐偭偰偄傞偐傜丄亄擖椡偲亅擖椡偺娫偺揹埑偼丄
|
倁
|
|
嘇
|
侾倠兌偺椉抂揹埑倁侾倠偼丄
|
倁
|
|
嘊
|
侾倠兌偵棳傟傞揹棳俬侾倠偼丄
|
倣俙
|
|
嘋
|
僆儁傾儞僾偺擖椡抂巕偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘍
|
俆倠兌偵棳傟傞揹棳俬俆倠偼丄
|
倣俙
|
|
嘐
|
俆倠兌偺椉抂揹埑倁俆倠偼丄
|
倁
|
|
嘑
|
弌椡揹埑倁俷偼丄
|
倁
|
|
嘒
|
忋懁乮俶俹俶僩儔儞僕僗僞偺乯倁俠俤偼丄
|
倁
|
|
嘓
|
晧壸偵棳傟傞揹棳俬俼俴偼丄
|
俙
|
|
嘔
|
僐儗僋僞揹棳俬俠偼丄
乮俬俆倠傪柍帇偡傞偲丄乯
|
俙
|
|
嘕
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤傪侾侽侽偲偡傞偲丄嘔偐傜丄乯
|
倣俙
|
|
嘖
|
僐儗僋僞懝幐俹俠偼丄
乮嘒偲嘔偐傜丄乯
|
倂
|
|
嘗
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
倁
|
|
嘙
|
俼俛偺椉抂揹埑倁俼俛偼丄
|
倁
|
|
嘚
|
僆儁傾儞僾偺弌椡抂巕偺揹埑倁俷俀偼丄
|
倁
|
俁.俀. 摎
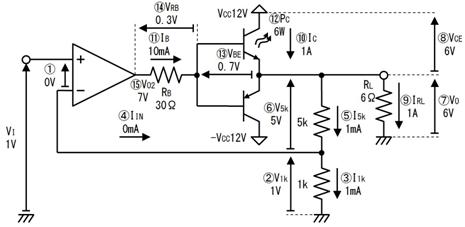
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
晧婣娨偑妡偐偭偰偄傞偐傜丄亄擖椡偲亅擖椡偺娫偺揹埑偼丄
|
侽倁
|
|
嘇
|
侾倠兌偺椉抂揹埑倁侾倠偼丄
|
侾倁
|
|
嘊
|
侾倠兌偵棳傟傞揹棳俬侾倠偼丄
|
侾倣俙
|
|
嘋
|
僆儁傾儞僾偺擖椡抂巕偵棳傟傞揹棳偼丄
|
侽倣俙
|
|
嘍
|
俆倠兌偵棳傟傞揹棳俬俆倠偼丄
|
侾倣俙
|
|
嘐
|
俆倠兌偺椉抂揹埑倁俆倠偼丄
|
俆倁
|
|
嘑
|
弌椡揹埑倁俷偼丄
|
俇倁
|
|
嘒
|
忋懁乮俶俹俶僩儔儞僕僗僞偺乯倁俠俤偼丄
|
俇倁
|
|
嘓
|
晧壸偵棳傟傞揹棳俬俼俴偼丄
|
侾俙
|
|
嘔
|
僐儗僋僞揹棳俬俠偼丄
乮俬俆倠傪柍帇偡傞偲丄乯
|
侾俙
|
|
嘕
|
儀乕僗揹棳俬俛偼丄
乮倛俥俤傪侾侽侽偲偡傞偲丄嘔偐傜丄乯
|
侾侽倣俙
|
|
嘖
|
僐儗僋僞懝幐俹俠偼丄
乮嘒偲嘔偐傜丄乯
|
俇倂
|
|
嘗
|
揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼丄
|
侽丏俈倁
|
|
嘙
|
俼俛偺椉抂揹埑倁俼俛偼丄
|
侽丏俁倁
|
|
嘚
|
僆儁傾儞僾偺弌椡抂巕偺揹埑倁俷俀偼丄
|
俈倁
|
忋昞偺傛偆偵懡偔偺応崌丄弌椡揹埑偑揹尮揹埑乮侾俀倁乯偺敿暘偺偲偒乮俇倁偺偲偒乯僄儈僢僞僼僅儘傾偺敪擬偑嵟戝偵側傝傑偡丅崱夞偺夞楬偼俇倂偺敪擬偑偁傝傑偡偐傜丄偦傟偵懴偊傞僩儔儞僕僗僞偲丄偦偺擬傪張棟偱偒傞曻擬婍偑昁梫偱偡丅
偝偰偙偺傛偆偵丄僆儁傾儞僾偲僐儞僾儕儊儞僞儕僄儈僢僞僼僅儘傾傪慻傒崌傢偣偰傕丄僋儘僗僆乕僶榗傒偼懡彮敪惗偟傑偡丅
僋儘僗僆乕僶榗傒傪尭傜偡嵟傕偍庤寉側曽朄傪壓恾偵帵偟傑偡丅壓恾偺夞楬偱偼丄儀乕僗僄儈僢僞娫偵俀俀兌偺掞峈傪捛壛偟偰偄傑偡丅
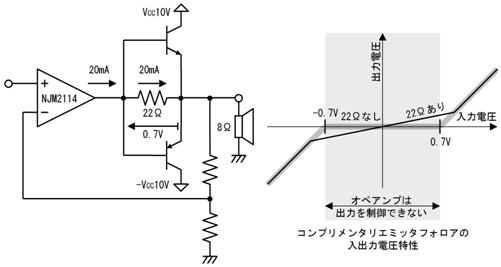
扨弮側僐儞僾儕儊儞僞儕僄儈僢僞僼僅儘傾偺擖弌椡揹埑摿惈偼丄壓恾塃懁偵奃怓慄偱帵偡傛偆偵丄擖椡偑亅侽丏俈倁乣侽丏俈倁偺娫偼弌椡偑曄壔偟傑偣傫丅偮傑傝偙偺揹埑斖埻偱偼丄僆儁傾儞僾偼弌椡揹埑傪惂屼偱偒傑偣傫丅偙偺偨傔丄榗傒傪梷偊傞偙偲傕偱偒傑偣傫丅偙偙偱俀俀兌傪捛壛偡傞偲丄偙偺揹埑斖埻偱嬐偐偱偼偁傝傑偡偑僆儁傾儞僾偑弌椡傪惂屼偱偒傞傛偆偵側傝傑偡丅偙偺偨傔丄夞楬偑娙扨側妱偵偼丄堄奜偲榗傒偑彮側偔側傝傑偡丅
偙偺夞楬偱偼丄僩儔儞僕僗僞偑摦嶌偟側偄丄亅侽丏俈倁乣侽丏俈倁偺娫偼丄俀俀兌傪捠偠偰僆儁傾儞僾偑捈愙晧壸偵揹棳傪棳偟傑偡偐傜丄弌椡揹棳偺戝偒側僆儁傾儞僾偑昁梫偱偡丅傑偨丄亅侽丏俈倁偐傜亄侽丏俈倁傑偱慺憗偔棫偪忋偑偭偰榗傒傪梷偊傜傟傞傛偆偵丄僗儖乕儗僀僩偺崅偄僆儁傾儞僾偑揔偟傑偡丅偙偙偱偼丄俶俰俵俀侾侾係傪巊梡偟偰偄傑偡丅
僋儘僗僆乕僶乕榗傪尭傜偡丄傛傝岠壥揑偱丄堦斒揑側曽朄傪壓恾偵帵偟傑偡丅摨恾乮倎乯偵帵偡傛偆偵丄僐儞僾儕儊儞僞儕僄儈僢僞僼僅儘傾偺儀乕僗偵乮倁俛俤偵憡摉偡傞乯僶僀傾僗揹埑傪乮婛偵愢柧偟偨曽朄偱乯僟僀僆乕僪偵傛偭偰壛偊傑偡丅
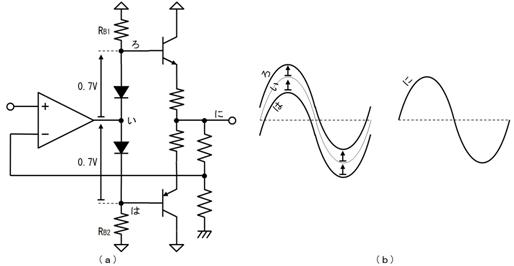
偙傟偵傛傝丄忋恾乮倐乯偵帵偡傛偆偵丄僆儁傾儞僾偺弌椡揹埑乮偄乯偵懳偟偰丄忋懁僩儔儞僕僗僞偺儀乕僗揹埑偼侽丏俈倁崅偔乮傠乯丄壓懁僩儔儞僕僗僞偺儀乕僗揹埑偼侽丏俈倁掅偔乮偼乯堐帩偝傟傑偡丅偙偺寢壥丄弌椡揹埑乮偵乯偼侽倁晅嬤偱傕妸傜偐偵曄壔偟丄僋儘僗僆乕僶榗偑側偔側傝傑偡丅
偲偙傠偑乮彂愋偱傕椙偔徯夘偝傟傞乯忋恾偺夞楬偼丄俼俛偑尨場偲側偭偰丄偁傑傝戝偒側弌椡揹棳傪棳偡偙偲偑偱偒傑偣傫丅
忋恾偺夞楬偱偼丄俼俛偑儀乕僗揹棳傪嫙媼偟傑偡偐傜丄俼俛偑戝偒偄偲弌椡揹棳偑彫偝偔側偭偰偟傑偄傑偡丅偱偡偐傜丄弌椡揹棳傪戝偒偔偡傞偨傔偵偼丄俼俛傪彫偝偔偟側偔偰偼側傝傑偣傫丅偲偙傠偑丄俼俛偼僆儁傾儞僾偺晧壸偲側偭偰偄傞偨傔丄俼俛傪彫偝偔偡傞偲丄僆儁傾儞僾偼戝偒側揹棳傪弌椡偟側偔偰偼側傝傑偣傫丅偟偐偟丄斈梡僆儁傾儞僾偺弌椡揹棳偼悢倣俙乣悢廫倣俙偲彫偝偄偺偱丄俼俛傪彫偝偔偡傞偙偲偼偱偒傑偣傫丅
偦偙偱丄壓恾乮倎乯偵帵偡傛偆側丄俼俛偺戙傝偵乮椉抂揹埑偵偐偐傢傜偢乯堦掕偺揹棳傪棳偡乽掕揹棳僟僀僆乕僪乿傪巊梡偟偨夞楬偑椙偔棙梡偝傟傑偡丅
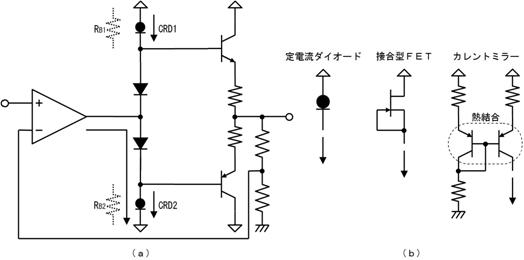
忋恾乮倐乯偺傛偆偵丄掕揹棳僟僀僆乕僪偺戙傝偵丄愙崌宆俥俤俿傗僇儗儞僩儈儗乕傪巊梡偡傞偙偲傕偱偒傑偡丅愙崌宆俥俤俿偺応崌偼揹棳偵屄懱嵎偑偁傞偺偱慖暿偑昁梫偱丄僇儗儞僩儈儔乕偼晹昳揰悢偑懡偔側傝傑偡偐傜丄忋恾乮倎乯偺傛偆偵丄掕揹棳僟僀僆乕僪傪梡偄傞曽朄偑妝偱偡丅
俁.俁. 楙廗
壓恾偺揹棳僽乕僗僞偺嵟戝弌椡揹棳傪丄壓昞偵彂偒崬傒側偑傜媮傔偰偔偩偝偄丅偨偩偟丄揹尮揹埑亇俋倁偱偺僆儁傾儞僾偺嵟崅乛嵟掅弌椡揹埑傪亇俈倁偲丄僆儁傾儞僾偼嵟戝弌椡揹棳傪侾侽倣俙偱巊梡偡傞偲峫偊傑偡丅
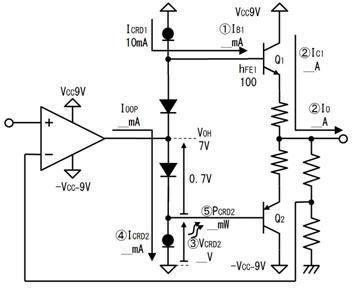
|
斣崋
|
幙栤
|
抣
|
|
|
僆儁傾儞僾偑嵟崅弌椡揹埑俈倁傪弌椡偟偰偄傞応崌傪峫偊傑偡丅
|
|
|
嘆
|
俠俼俢侾偺揹棳偑慡偰俻侾偺傋乕僗偵棳傟偨偲偡傟偽丄儀乕僗揹棳俬俛侾偼丄
|
倣俙
|
|
嘇
|
揹棳僽乕僗僞偺弌椡揹棳俬俷丄偮傑傝俻侾偺僐儗僋僞揹棳俬俠侾偼丄
乮倛俥俥偑侾侽侽偩偐傜乯
|
俙
|
|
嘊
|
俠俼俢俀偺椉抂揹埑倁俠俼俢俀偼丄
乮僆儁傾儞僾偺嵟崅弌椡揹埑偲丄僟僀僆乕僪偺弴揹埑偐傜丄乯
|
倁
|
|
嘋
|
俠俼俢俀偵棳傟傞揹棳俬俠俼俢俀偼丄
|
倣俙
|
|
嘍
|
俠俼俢俀偺徚旓揹椡俹俠俼俢俀偼丄
|
倣倂
|
|
嘐
|
僆儁傾儞僾偺弌椡揹棳俬俷俷俹偼丄
|
倣俙
|
俁.係. 摎
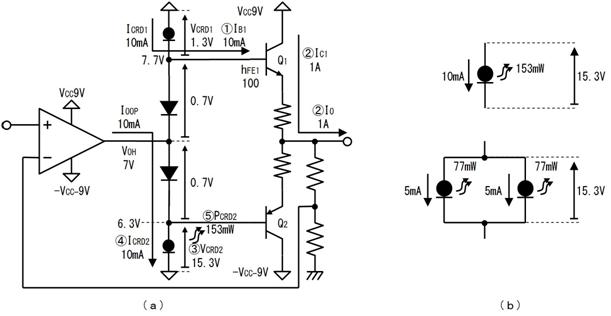
|
斣崋
|
幙栤
|
抣
|
|
|
僆儁傾儞僾偑嵟崅弌椡揹埑俈倁傪弌椡偟偰偄傞応崌傪峫偊傑偡丅
|
|
|
嘆
|
俠俼俢侾偺揹棳偑慡偰俻侾偺傋乕僗偵棳傟偨偲偡傟偽丄儀乕僗揹棳俬俛侾偼丄
|
侾侽倣俙
|
|
嘇
|
揹棳僽乕僗僞偺弌椡揹棳俬俷丄偮傑傝俻侾偺僐儗僋僞揹棳俬俠侾偼丄
乮倛俥俥偑侾侽侽偩偐傜乯
|
侾俙
|
|
嘊
|
俠俼俢俀偺椉抂揹埑倁俠俼俢俀偼丄
乮僆儁傾儞僾偺嵟崅弌椡揹埑偲丄僟僀僆乕僪偺弴揹埑偐傜丄乯
|
侾俆丏俁倁
|
|
嘋
|
俠俼俢俀偵棳傟傞揹棳俬俠俼俢俀偼丄
|
侾侽倣俙
|
|
嘍
|
俠俼俢俀偺徚旓揹椡俹俠俼俢俀偼丄
|
侾俆俁倣倂
|
|
嘐
|
僆儁傾儞僾偺弌椡揹棳俬俷俷俹偼丄
|
侾侽倣俙
|
忋昞偱暘偐傞傛偆偵丄俠俼俢偺揹棳偺倛俥俤攞偑丄揹棳僽乕僗僞偺嵟戝弌椡揹棳偲側傝丄傑偨丄俠俼俢偺揹棳偼僆儁傾儞僾偺嵟戝弌椡揹棳偲側傝傑偡丅
偮傑傝丄乮敪擬傕娷傔偰専摙偟乯僆儁傾儞僾偑侾侽倣俙棳偡偙偲偑偱偒傟偽丄俠俼俢偼侾侽倣俙偺昳庬傪慖傃丄揹棳僽乕僗僞偼侾侽倣俙亊侾侽侽亖侾俙偺揹棳傪弌椡偱偒傑偡丅媡偵丄侾俙弌椡偟偨偄応崌偼丄侾俙乛倛俥俤亖侾侽倣俙偺俠俼俢傪慖傃丄僆儁傾儞僾偼侾侽倣俙偺弌椡揹棳偑昁梫偱偡丅
傑偨丄嵟崅揹埑傪弌椡偟偨偲偒偵丄俠俼俢俀偺徚旓揹椡偑嵟崅偵側傝傑偡丅彫宍俠俼俢偺嵟戝掕奿偼俁侽侽倣倂掱搙偱偡偐傜丄忋昞偺侾俆俁倣倂偼婥壏偑崅偄偲尩偟偄忬懺偱偡丅偙偺傛偆側応崌丄忋恾乮倐乯偺傛偆偵丄俆倣俙偺俠俼俢傪暲楍偵愙懕偡傞偙偲偱丄慺巕侾偮偁偨傝偺揹椡傪尭傜偡偙偲偑偱偒傑偡丅
俁.俆. 楙廗
壓恾傪嶲峫偵丄壓昞偵彂偒崬傒側偑傜丄夞楬偑侽倁傪弌椡偟偰偄傞偲偒丄傾僀僪儕儞僌揹棳乮侽倁弌椡帪偺僄儈僢僞揹棳乯偑俁侽倣俙偲側傞傛偆丄俼俤偺抣傪寛掕偟偰壓偝偄丅傑偨丄偦偺偲偒偺俻侾偺徚旓揹椡乮僐儗僋僞懝幐乯傪媮傔偰壓偝偄丅偨偩偟丄僟僀僆乕僪偺弴揹埑傪侽丏俈倁偲丄俻侾偼敪擬偵傛傝乮栺俆侽亷壏搙忋徃偟偰乯倁俛俤偑侽丏俇倁偵掅壓偟偨偲峫偊偰偔偩偝偄丅
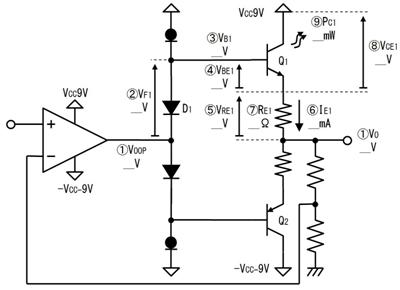
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
夞楬偺弌椡揹埑偲僆儁傾儞僾偺弌椡揹埑偼嫟偵丄
乮偙偙偱偼丄侽倁弌椡帪傪峫偊傞偐傜丄乯
|
倁
|
|
嘇
|
忢壏偺僟僀僆乕僪俢侾偺弴揹埑倁俥侾偼丄
|
倁
|
|
嘊
|
俻侾偺儀乕僗揹埑倁俛侾偼丄
|
倁
|
|
嘋
|
敪擬偟偨俻侾偺倁俛俤侾偼丄
乮栺俆侽亷壏搙忋徃偟偰偄傞偐傜丄乯
|
倁
|
|
嘍
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
|
倁
|
|
嘐
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
乮傾僀僪儕儞僌揹棳傪俁侽倣俙偲偡傞偐傜丄乯
|
倣俙
|
|
嘑
|
僄儈僢僞掞峈俼俤偺抣偼丄
乮嘍偲嘐偐傜丄乯
|
兌
|
|
嘒
|
偙偺偲偒偺俻侾偺倁俠俤偼丄
乮嘍偲倁俠俠俋倁偐傜丄乯
|
倁
|
|
嘓
|
偙偺偲偒偺俻侾偺僐儗僋僞懝幐俹俠侾偼丄
|
倣倂
|
|
嘔
|
摨條偵峫偊偰俻俀偺僐儗僋僞懝幐俹俠俀偼丄
|
倣倂
|
俁.俇. 摎
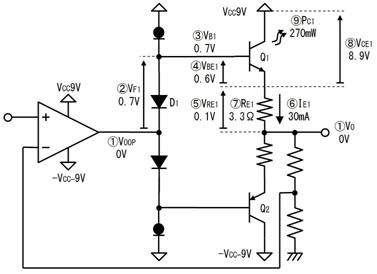
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
夞楬偺弌椡揹埑偲僆儁傾儞僾偺弌椡揹埑偼嫟偵丄
乮偙偙偱偼丄侽倁弌椡帪傪峫偊傞偐傜丄乯
|
侽倁
|
|
嘇
|
忢壏偺僟僀僆乕僪俢侾偺弴揹埑倁俥侾偼丄
|
侽丏俈倁
|
|
嘊
|
俻侾偺儀乕僗揹埑倁俛侾偼丄
|
侽丏俈倁
|
|
嘋
|
敪擬偟偨俻侾偺倁俛俤侾偼丄
乮栺俆侽亷壏搙忋徃偟偰偄傞偐傜丄乯
|
侽丏俇倁
|
|
嘍
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
|
侽丏侾倁
|
|
嘐
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
乮傾僀僪儕儞僌揹棳傪俁侽倣俙偲偡傞偐傜丄乯
|
俁侽倣俙
|
|
嘑
|
僄儈僢僞掞峈俼俤偺抣偼丄
乮嘍偲嘐偐傜丄乯
|
俁俁兌
|
|
嘒
|
偙偺偲偒偺俻侾偺倁俠俤偼丄
乮嘍偲倁俠俠俋倁偐傜丄乯
|
俉丏俋倁
|
|
嘓
|
偙偺偲偒偺俻侾偺僐儗僋僞懝幐俹俠侾偼丄
|
俀俈侽倣倂
|
|
嘔
|
摨條偵峫偊偰俻俀偺僐儗僋僞懝幐俹俠俀偼丄
|
俀俈侽倣倂
|
俁.俈. 楙廗
壓恾傪嶲峫偵壓昞偵彂偒崬傒側偑傜丄夞楬偑嵟戝揹棳乮侾俙乯傪弌椡偟偰偄傞偲偒偺丄嵟戝弌椡揹埑傪媮傔偰偔偩偝偄丅扐偟僆儁傾儞僾偺嵟戝弌椡揹埑傪俈倁偲偟傑偡丅
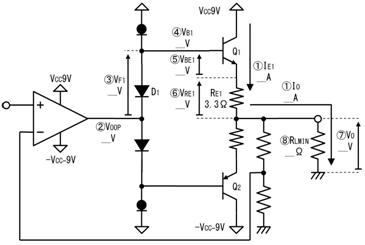
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺嵟戝僄儈僢僞揹棳俬俤侾偼丄
|
俙
|
|
嘇
|
僆儁傾儞僾偺嵟戝弌椡揹埑倁俷俷俹偼丄
|
倁
|
|
嘊
|
僟僀僆乕僪俢侾偺弴揹埑倁俥侾偼丄
|
倁
|
|
嘋
|
俻侾偺儀乕僗揹埑倁俛侾偼丄
|
倁
|
|
嘍
|
俻侾偺倁俛俤偼敪擬偟偰偄傞偲峫偊偰丄
|
倁
|
|
嘐
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
乮嘆偲僄儈僢僞掞峈偺抣偐傜丄乯
|
倁
|
|
嘑
|
夞楬偺弌椡揹埑倁俷偼丄
|
倁
|
|
嘒
|
夞楬偵愙懕偱偒傞晧壸掞峈俼俴偺嵟掅抣偼丄
乮嘆偲嘑偐傜丄乯
|
兌
|
俁.俉. 摎
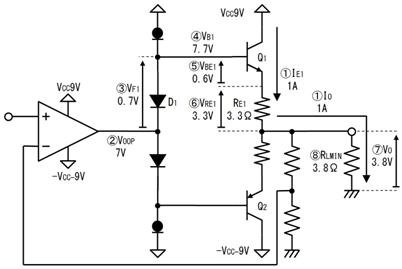
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺嵟戝僄儈僢僞揹棳俬俤侾偼丄
|
侾俙
|
|
嘇
|
僆儁傾儞僾偺嵟戝弌椡揹埑倁俷俷俹偼丄
|
俈倁
|
|
嘊
|
僟僀僆乕僪俢侾偺弴揹埑倁俥侾偼丄
|
侽丏俈倁
|
|
嘋
|
俻侾偺儀乕僗揹埑倁俛侾偼丄
|
俈丏俈倁
|
|
嘍
|
俻侾偺倁俛俤偼敪擬偟偰偄傞偲峫偊偰丄
|
侽丏俇倁
|
|
嘐
|
僄儈僢僞掞峈偺椉抂揹埑倁俼俤侾偼丄
乮嘆偲僄儈僢僞掞峈偺抣偐傜丄乯
|
俁丏俁倁
|
|
嘑
|
夞楬偺弌椡揹埑倁俷偼丄
|
俁丏俉倁
|
|
嘒
|
夞楬偵愙懕偱偒傞晧壸掞峈俼俴偺嵟掅抣偼丄
乮嘆偲嘑偐傜丄乯
|
俁丏俉兌
|
偙偺傛偆偵丄俼俤偺抣偑戝偒偄偲丄嵟戝弌椡揹埑偑彫偝偔側傝傑偡丅僟僀僆乕僪偲僩儔儞僕僗僞偺擬寢崌傪偟偭偐傝峴偆偙偲偱丄椉幰偺壏搙傪嬤偯偗傞偙偲偑偱偒丄俼俤偺抣傪彫偝偔偡傞偙偲偑偱偒傑偡丅
俁.俋. 楙廗
倁俠俤侾偑揹尮揹埑倁俠俠偺敿暘偲側偭偨偲偒丄俻侾偺僐儗僋僞懝幐俹俠侾偑嵟戝偵側傝傑偡丅壓恾傪嶲峫偵壓昞偵彂偒崬傒側偑傜丄俻侾偺嵟戝偺僐儗僋僞懝幐俹俠俵俙倃侾傪媮傔偰偔偩偝偄丅扐偟丄夞楬偺晧壸偲偟偰俁丏俉兌偺掞峈傪愙懕偟偨偲峫偊傑偡丅
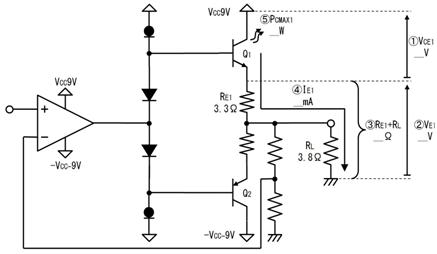
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺僐儗僋僞僄儈僢僞娫揹埑丄倁俠俤侾偼丄
乮倁俠俠偺敿暘偩偐傜丄乯
|
倁
|
|
嘇
|
俻侾偺僄儈僢僞揹埑倁俤侾偼丄
乮倁俠俠偲嘆偐傜丄乯
|
倁
|
|
嘊
|
俼俤侾偲俼俴偺捈楍崌惉掞峈偼丄
|
兌
|
|
嘋
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
乮嘇偲嘊偐傜丄乯
|
倣倂
|
|
嘍
|
俻侾偺嵟戝懝幐俹俠俵俙倃侾偼丄
|
倂
|
俁.侾侽. 摎
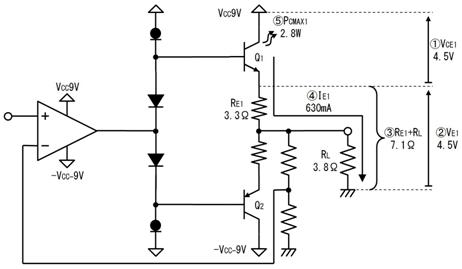
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
俻侾偺僐儗僋僞僄儈僢僞娫揹埑丄倁俠俤侾偼丄
乮倁俠俠偺敿暘偩偐傜丄乯
|
係丏俆倁
|
|
嘇
|
俻侾偺僄儈僢僞揹埑倁俤侾偼丄
乮倁俠俠偲嘆偐傜丄乯
|
係丏俆倁
|
|
嘊
|
俼俤侾偲俼俴偺捈楍崌惉掞峈偼丄
|
俈丏侾兌
|
|
嘋
|
俻侾偺僄儈僢僞揹棳俬俤侾偼丄
乮嘇偲嘊偐傜丄乯
|
俇俁侽倣倂
|
|
嘍
|
俻侾偺嵟戝懝幐俹俠俵俙倃侾偼丄
|
俀丏俉倂
|
係. 埨掕壔揹尮夞楬
桪傟偨惈擻偺俁抂巕儗僊儏儗乕僞偑埨壙偵弌夞偭偰偄傞偨傔丄埨掕壔揹尮傪庤嶌傝偡傞昁梫偼杦偳偁傝傑偣傫丅偙偙偱偼夞楬峔惉傪夝愢偡傞栚揑偱丄埨掕壔揹尮傪愢柧偟傑偡丅
壓恾乮倎乯偺夞楬偼丄俋倁偺埨掕壔揹尮夞楬偱偡丅婛偵愢柧偟偨丄揹棳僽乕僗僞晅偺俁攞偺旕斀揮憹暆婍偵丄僣僃乕僫僟僀僆乕僪偱敪惗偝偣偨俁倁傪擖椡偟丄埨掕偟偨俋倁傪弌椡偟傑偡丅偮傑傝丄埨掕壔揹尮夞楬偲偼丄堦掕偺揹埑傪弌椡偡傞戝弌椡偺憹暆婍偱偡丅
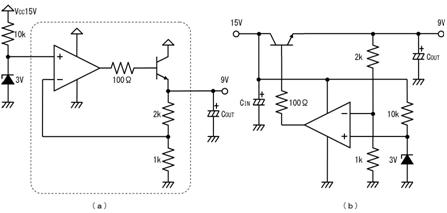
忋恾乮倐乯偼丄幚偼忋恾乮倎乯偲慡偔摨偠夞楬偱丄彂偒曽偑曄傢偭偨偩偗偱偡丅僆儁傾儞僾夞楬傪揹尮夞楬偵棙梡偡傞偲偒偼丄忋恾乮倐乯偺傛偆偵彂偔応崌偑杦偳偱偡丅側偤側傜丄捠忢偺夞楬偱偼徣棯偝傟傞倁俠俠偑丄揹尮夞楬偱偼乽夞楬偺擖椡乿偲側傞偺偱丄倁俠俠偺攝慄傪嬶懱揑偵帵偟偨偄偐傜偱偡丅
埨掕壔揹尮夞楬偺弌椡揹埑偼堦掕偱偡偐傜丄忋恾偺俠俷倀俿傪庢傝晅偗偰傕僩儔儞僕僗僞偺晧扴偼憹偝偢丄媡偵丄媫偵揹棳偑棳傟偨偲偒偵丄俠俷倀俿偑曻揹偟偰偦偺揹棳傪嫙媼偟偰偔傟傞偺偱岲搒崌偱偡丅偨偩偟丄拞搑敿抂側梕検偺俠俷倀俿傪庢傝晅偗傞偲丄僆儁傾儞僾偑廩曻揹傪孞傝曉偟偰夞楬偑晄埨掕偵側傞偨傔丄廫暘戝偒側梕検偺僐儞僨儞僒傪巊梡偟傑偡丅
壓恾偼僣僃乕僫僟僀僆乕僪偺戙傝偵丄傛傝埨掕側婎弨揹埑梡俬俠乮俴俵係俁侾乯傪棙梡偟偰丄儃儕僂儉偱弌椡揹埑傪壜曄偵偟偨揹尮夞楬偺椺偱偡丅俻侾偲俻俀偼僟乕儕儞僩儞愙懕偱戝偒側弌椡揹棳傪棳偡偙偲偑偱偒傑偡丅
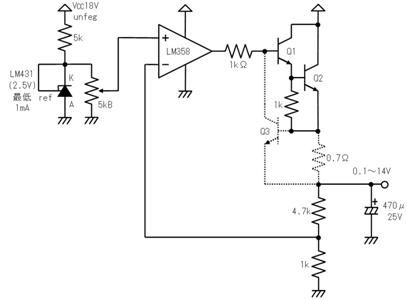
恾偵揰慄偱帵偡夞楬偼娙堈曐岇夞楬偱丄侽丏俈兌偺椉抂揹埑偑侽丏俈倁傪挻偊傞偲丄俻俁偑俷俶偵側傝丄俻侾偺儀乕僗揹埑傪壓偘偰丄弌椡揹棳偑偦傟埲忋憹偊側偄傛偆偵偟傑偡丅忋偺夞楬偱偼栺侾俙偱曐岇偑妡偐傝傑偡丅曐岇偑妡偐偭偰偄傞偲偼尵偊丄侾俙偺揹棳偑棳傟懕偗傑偡偐傜丄戝偒側敪擬偑偁傝傑偡丅偱偡偐傜丄曐岇偺妡偐偭偨忬懺偱楢懕巊梡偡傞偙偲偼偱偒傑偣傫丅乮夁偭偰丄弌椡傪僔儑乕僩偝偣偨弖娫偵僩儔儞僕僗僞偑夡傟側偄偨傔偺傕偺偱偡丅乯
偙偺夞楬峔惉偱侽倁偵嬤偄揹埑傪弌椡偡傞偨傔偵偼丄亅揹尮揹埑乮偙偙偱偼侽倁乯晅嬤偺擖椡揹埑偱惓忢摦嶌偡傞僆儁傾儞僾偑昁梫偱偡丅俴俵俁俆俉偙偺傛偆側栚揑偱棙梡偱偒傞埨壙側僆儁傾儞僾偱丄愝寁偼屆偄偱偡偑傑偩傑偩巊偊傑偡丅
埨掕壔揹尮夞楬偼丄條乆側晧壸傪宷偄偱巊梡偡傞偨傔丄敪怳偡傞応崌偑偁傝傑偡丅偙偺傛偆側応崌丄俠俷倀俿傪戝偒偔偡傞偐丄憹暆婍偺憹暆棪傪忋偘傑偡丅偨偲偊偽丄忋恾偺夞楬偱偼俆丏俈攞偱偡偑丄俀侽攞丄俁侽攞丄偲偄偆傛偆偵憹暆棪傪忋偘傟偽乮偦偺暘亄擖椡抂巕偺揹埑傪壓偘傑偡乯敪怳偼帯傑傝傑偡丅
壓恾偼僆儁傾儞僾偱惓妋偝傪崅傔偨掕揹棳夞楬偱偡丅傑偨丄擖椡揹埑偱揹棳傪曄壔偝偣傞偙偲傕偱偒傑偡丅
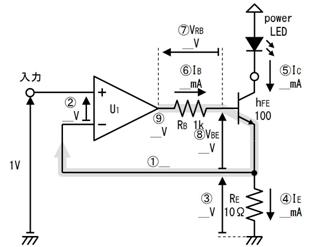
俆.侾. 楙廗
忋恾偺夞楬偺摦嶌傪壓昞偵彂偒崬傒側偑傜妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
偙偺夞楬偼晧婣娨偑妡偐偭偰偄傑偡偐丅
乮慖傫偱壓偝偄乯
|
妡偐偭偰偄傞
妡偐偭偰偄側偄
|
|
嘇
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
乮嘆偐傜丄乯
|
倁
|
|
嘊
|
侾侽侽兌偺椉抂揹埑偼丄
|
倁
|
|
嘋
|
侾侽侽兌偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘍
|
僐儗僋僞揹棳乮弌椡揹棳乯偼丄
|
倣俙
|
|
嘐
|
儀乕僗揹棳偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
倣俙
|
|
嘑
|
儀乕僗掞峈偺椉抂揹埑偼丄
|
倁
|
|
嘒
|
倁俛俤偼丄
|
倁
|
|
嘓
|
僆儁傾儞僾偺弌椡揹埑偼丄
|
倁
|
俆.俀. 摎
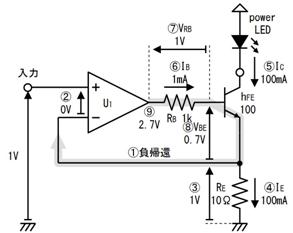
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
偙偺夞楬偼晧婣娨偑妡偐偭偰偄傑偡偐丅
乮慖傫偱壓偝偄乯
|
妡偐偭偰偄傞
妡偐偭偰偄側偄
|
|
嘇
|
亄擖椡偲亅擖椡偺娫偺揹埑偼丄
乮嘆偐傜丄乯
|
侽倁
|
|
嘊
|
侾侽侽兌偺椉抂揹埑偼丄
|
侾倁
|
|
嘋
|
侾侽侽兌偵棳傟傞揹棳偼丄
|
侾侽侽倣俙
|
|
嘍
|
僐儗僋僞揹棳乮弌椡揹棳乯偼丄
|
侾侽侽倣俙
|
|
嘐
|
儀乕僗揹棳偼丄
乮倛俥俤偑侾侽侽偩偐傜丄乯
|
侾倣俙
|
|
嘑
|
儀乕僗掞峈偺椉抂揹埑偼丄
|
侾倁
|
|
嘒
|
倁俛俤偼丄
|
侽丏俈倁
|
|
嘓
|
僆儁傾儞僾偺弌椡揹埑偼丄
|
俀丏俈倁
|
扨堦揹尮偱忋恾偺夞楬傪摦嶌偝偣傞応崌偼丄侽倁晅嬤偺揹埑傪擖弌椡偱偒傞扨堦揹尮梡僆儁傾儞僾乮俴俵俁俆俉傗俴俵俀俋侽係摍乯傪巊梡偟傑偡丅
壓恾乮倎乯偺傛偆偵扨揹尮梡僆儁傾儞僾乮偁傞偄偼丄儗乕儖僩僁儗僀儖僆儁傾儞僾乯傪梡偄傟偽丄儅僀僫僗揹尮偵岦偐偭偰傾乕僗偐傜揹棳傪媧偄崬傓摦嶌偑偱偒傑偡丅偨偩偟丄擖椡揹埑偼儅僀僫僗揹尮傪婎弨偲偟偰壛偊傞昁梫偑偁傝傑偡丅
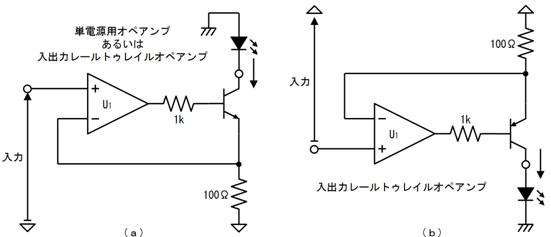
忋恾乮倐乯偺傛偆偵丄俹俶俹僩儔儞僕僗僞偲儗乕儖僩僁儗僀儖僆儁傾儞僾傪梡偄傟偽丄僾儔僗揹尮偐傜傾乕僗偵岦偐偭偰揹棳傪揻偒弌偡摦嶌傕偱偒傑偡丅偨偩偟丄擖椡揹埑偼僾儔僗揹尮傪婎弨偲偟偰壛偊傞昁梫偑偁傝傑偡丅
壓恾偵帵偡傛偆偵丄俵俷俽俥俤俿乮俶僠儍僱儖乯傪梡偄傟偽丄僆儁傾儞僾偺弌椡揹棳偑彫偝偔偰傕丄戝偒側揹棳傪惂屼偱偒傑偡丅
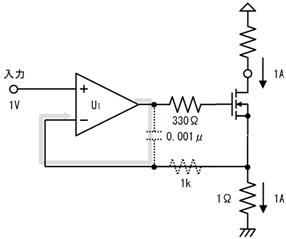
戝宆偺俵俷俽俥俤俿偺僎乕僩偵偼戝偒側梕検偑偁傞偺偱丄僆儁傾儞僾偱偼慺憗偔廩揹偱偒傑偣傫丅偦偺偨傔摦嶌偑抶傟偰敪怳偡傞応崌偑偁傝傑偡丅偙偺応崌丄忋恾偵揰慄偱帵偡傛偆偵侾倠兌偲侽丏侽侽侾兪俥傪捛壛偟偰丄崅偄廃攇悢偱偼丄僆儁傾儞僾偺弌椡偑捈愙亅擖椡偵晧婣娨偝傟傞傛偆偵偟傑偡丅乮俀俶俈侽侽侽摍偺彫宍俵俷俽俥俤俿偱偼丄偙偺俠俼偼昁梫偁傝傑偣傫丅乯
壓恾偺傛偆偵俹僠儍僱儖俵俷俽俥俤俿傪梡偄傟偽丄揹棳傪揻偒弌偡掕揹棳夞楬傪嶌傞偙偲偑偱偒傑偡丅
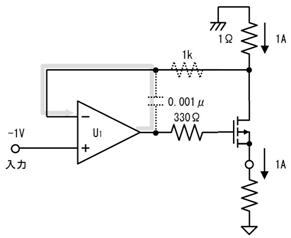
壓恾偼乽儂乕儔儞僪夞楬乮儂乕儔儞僪偺揹棳億儞僾丗Howland Current Pump乯乿偲偄偆掕揹棳夞楬偱丄戝偒側揹棳偼棳偣傑偣傫偑丄揹棳傪揻偒弌偡偙偲傕丄媧偄崬傓偙偲傕偱偒傑偡丅傑偨丄擖椡抂巕偺揹埑偱丄棳偡揹棳傪帺桼偵曄峏偱偒傑偡丅
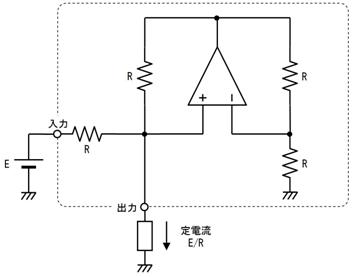
儂乕儔儞僪夞楬偼丄擖椡抂巕偺揹埑偱寛傑傞揹棳傪丄乮弌椡抂巕偵壛傢傞揹埑傗丄愙懕偡傞晧壸偵娭學側偔乯弌椡抂巕偵棳偡偙偲偺偱偒傞掕揹棳夞楬偱偡丅
俇.侾. 妋擣
壓恾傪嶲峫偵壓昞偵彂偒崬傫偱丄擖椡抂巕偵俁倁丄弌椡抂巕偵侾倁傪壛偊偨応崌偺丄儂乕儔儞僪夞楬偺弌椡揹棳傪妋擣偟偰偔偩偝偄丅
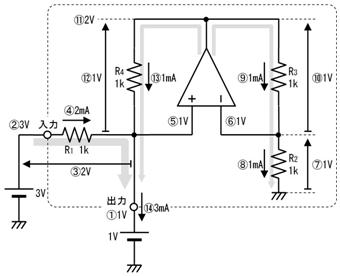
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
弌椡抂巕偺揹埑偼丄
乮侾倁偺揹抮偑愙懕偝傟偰偄傞偺偱丄乯
|
倁
|
|
嘇
|
擖椡抂巕偺揹埑偼丄
乮俁倁偺揹抮偑愙懕偝傟偰偄傞偺偱丄乯
|
倁
|
|
嘊
|
俼侾偺椉抂揹埑偼丄
乮嘆偲嘇偐傜丄乯
|
倁
|
|
嘋
|
俼侾偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘍
|
亅擖椡偺揹埑偼丄乮嘆偐傜丄乯
|
倁
|
|
嘐
|
亄擖椡偺揹埑偼丄
乮嘍偲丄俼係偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
倁
|
|
嘑
|
俼俀偺椉抂揹埑偼丄乮嘐偐傜丄乯
|
倁
|
|
嘒
|
俼俀偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘓
|
俼俁偵棳傟傞揹棳偼丄
乮擖椡抂巕偵偼揹棳偑棳傟側偄偐傜丄乯
|
倣俙
|
|
嘔
|
俼俁偺椉抂揹埑偼丄
|
倁
|
|
嘕
|
僆儁傾儞僾偺弌椡抂巕偺揹埑偼丄乮嘑偲嘔偐傜丄乯
|
倁
|
|
嘖
|
俼係偺椉抂揹埑偼丄乮嘍偲嘕偐傜丄乯
|
倁
|
|
嘗
|
俼係偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘙
|
弌椡抂巕偐傜棳傟弌偡揹棳偼丄
乮嘋偲嘗偐傜丄乯
|
倣俙
|
俇.俀. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
弌椡抂巕偺揹埑偼丄
乮侾倁偺揹抮偑愙懕偝傟偰偄傞偺偱丄乯
|
侾倁
|
|
嘇
|
擖椡抂巕偺揹埑偼丄
乮俁倁偺揹抮偑愙懕偝傟偰偄傞偺偱丄乯
|
俁倁
|
|
嘊
|
俼侾偺椉抂揹埑偼丄
乮嘆偲嘇偐傜丄乯
|
俀倁
|
|
嘋
|
俼侾偵棳傟傞揹棳偼丄
|
俀倣俙
|
|
嘍
|
亅擖椡偺揹埑偼丄乮嘆偐傜丄乯
|
侾倁
|
|
嘐
|
亄擖椡偺揹埑偼丄
乮嘍偲丄俼係偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
侾倁
|
|
嘑
|
俼俀偺椉抂揹埑偼丄乮嘐偐傜丄乯
|
侾倁
|
|
嘒
|
俼俀偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘓
|
俼俁偵棳傟傞揹棳偼丄
乮擖椡抂巕偵偼揹棳偑棳傟側偄偐傜丄乯
|
侾倣俙
|
|
嘔
|
俼俁偺椉抂揹埑偼丄
|
侾倁
|
|
嘕
|
僆儁傾儞僾偺弌椡抂巕偺揹埑偼丄乮嘑偲嘔偐傜丄乯
|
俀倁
|
|
嘖
|
俼係偺椉抂揹埑偼丄乮嘍偲嘕偐傜丄乯
|
侾倁
|
|
嘗
|
俼係偵棳傟傞揹棳偼丄
|
侾倣俙
|
|
嘙
|
弌椡抂巕偐傜棳傟弌偡揹棳偼丄
乮嘋偲嘗偐傜丄乯
|
俁倣俙
|
俇.俁. 楙廗
壓恾傪嶲峫偵壓昞偵彂偒崬傫偱丄擖椡抂巕偵俁倁丄弌椡抂巕偵亅俀倁傪壛偊偨応崌偺丄儂乕儔儞僪夞楬偺弌椡揹棳傪妋擣偟偰偔偩偝偄丅乮揹埑丒揹棳偼栴報偺岦偒傪僾儔僗偲偟偰婰擖偟偰偔偩偝偄乯
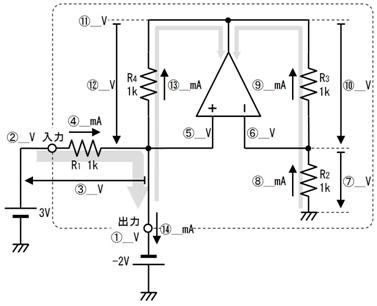
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
弌椡抂巕偺揹埑偼丄
乮亅俀倁偺揹抮偑愙懕偝傟偰偄傞偺偱丄乯
|
倁
|
|
嘇
|
擖椡抂巕偺揹埑偼丄
乮俁倁偺揹抮偑愙懕偝傟偰偄傞偺偱丄乯
|
倁
|
|
嘊
|
俼侾偺椉抂揹埑偼丄
乮嘆偲嘇偐傜丄乯
|
倁
|
|
嘋
|
俼侾偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘍
|
亅擖椡偺揹埑偼丄乮嘆偐傜丄乯
|
倁
|
|
嘐
|
亄擖椡偺揹埑偼丄
乮嘍偲丄俼係偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
倁
|
|
嘑
|
俼俀偺椉抂揹埑偼丄乮嘐偐傜丄乯
|
倁
|
|
嘒
|
俼俀偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘓
|
俼俁偵棳傟傞揹棳偼丄
乮擖椡抂巕偵偼揹棳偑棳傟側偄偐傜丄乯
|
倣俙
|
|
嘔
|
俼俁偺椉抂揹埑偼丄
|
倁
|
|
嘕
|
僆儁傾儞僾偺弌椡抂巕偺揹埑偼丄乮嘑偲嘔偐傜丄乯
|
倁
|
|
嘖
|
俼係偺椉抂揹埑偼丄乮嘍偲嘕偐傜丄乯
|
倁
|
|
嘗
|
俼係偵棳傟傞揹棳偼丄
|
倣俙
|
|
嘙
|
弌椡抂巕偐傜棳傟弌偡揹棳偼丄
乮嘋偲嘗偐傜丄乯
|
倣俙
|
俇.係. 摎
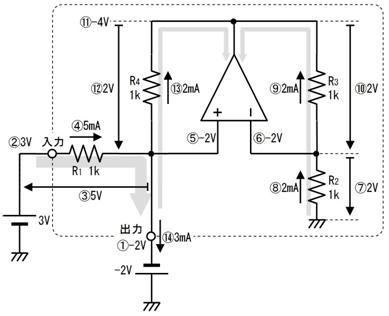
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
弌椡抂巕偺揹埑偼丄
乮亅俀倁偺揹抮偑愙懕偝傟偰偄傞偺偱丄乯
|
亅俀倁
|
|
嘇
|
擖椡抂巕偺揹埑偼丄
乮俁倁偺揹抮偑愙懕偝傟偰偄傞偺偱丄乯
|
俁倁
|
|
嘊
|
俼侾偺椉抂揹埑偼丄
乮嘆偲嘇偐傜丄乯
|
俆倁
|
|
嘋
|
俼侾偵棳傟傞揹棳偼丄
|
俆倣俙
|
|
嘍
|
亅擖椡偺揹埑偼丄乮嘆偐傜丄乯
|
亅俀倁
|
|
嘐
|
亄擖椡偺揹埑偼丄
乮嘍偲丄俼係偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
亅俀倁
|
|
嘑
|
俼俀偺椉抂揹埑偼丄乮嘐偐傜丄乯
|
俀倁
|
|
嘒
|
俼俀偵棳傟傞揹棳偼丄
|
俀倣俙
|
|
嘓
|
俼俁偵棳傟傞揹棳偼丄
乮擖椡抂巕偵偼揹棳偑棳傟側偄偐傜丄乯
|
俀倣俙
|
|
嘔
|
俼俁偺椉抂揹埑偼丄
|
俀倁
|
|
嘕
|
僆儁傾儞僾偺弌椡抂巕偺揹埑偼丄乮嘑偲嘔偐傜丄乯
|
係倁
|
|
嘖
|
俼係偺椉抂揹埑偼丄乮嘍偲嘕偐傜丄乯
|
侾倁
|
|
嘗
|
俼係偵棳傟傞揹棳偼丄
|
俀倣俙
|
|
嘙
|
弌椡抂巕偐傜棳傟弌偡揹棳偼丄
乮嘋偲嘗偐傜丄乯
|
俁倣俙
|
偙偺傛偆偵丄儂乕儔儞僪夞楬偼弌椡抂巕偺揹埑偑曄壔偟偰傕丄弌椡抂巕偵偼堦掕偺揹棳偑棳傟傑偡丅
壓恾偼幚梡揑側乮崅惛搙偺乯儂乕儔儞僪夞楬偱偡丅儂乕儔儞僪夞楬偼掞峈偺斾棪偑丄偁丗偄 亖 偆丗偊
偺帪偵惓妋偵摦嶌偟傑偡丅偙偺偨傔敿屌掕掞峈偱 偆丗偊 偺斾棪傪挷愡偱偒傞傛偆偵岺晇偝傟偰偄傑偡丅俆倫偺僐儞僨儞僒偼敪怳杊巭偱偡丅乮惛搙偺昁梫側偄応崌偼挷惍傪徣棯偱偒傑偡乯
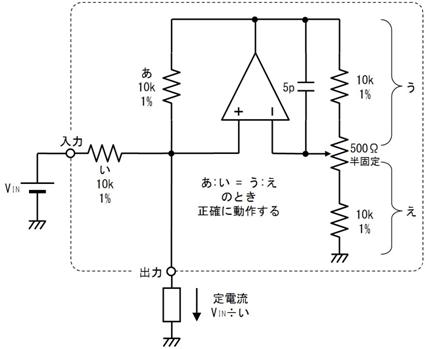
敿屌掕偺挷惍曽朄偼師偺偲偍傝偱偡丅嘆敿屌掕傪乽偊乿偺曽岦偵堦攖夞偟傑偡丅嘇擖椡傪侽倁偵愙懕偟丄弌椡偵偼壗傕愙懕偟側偄忬懺偱丄僆儁傾儞僾偺弌椡揹埑傪應掕偟傑偡丅乮揹埑偼侽倁偱偡乯嘊敿屌掕傪乽偆乿偺曽岦偵夞偟偰峴偔偲丄僆儁傾儞僾偺弌椡揹埑偑媫偵忋徃乮偁傞偄偼丄崀壓乯偡傞埵抲偑偁傝傑偡丅偦偺悺慜偑惓偟偄愝掕埵抲偱偡丅
壓恾偼夵椙宆偺儂乕儔儞僪夞楬偱乽偄乿偺掞峈傪戝偒偔偱偒傞偨傔丄擖椡抂巕偵棳傟崬傓揹棳偑嬐偐偱嵪傒傑偡丅傑偨乽偍乿偺掞峈傪彫偝偔偱偒傞偺偱丄弌椡偵岠棪椙偔揹棳傪棳偡偙偲偑偱偒傑偡丅
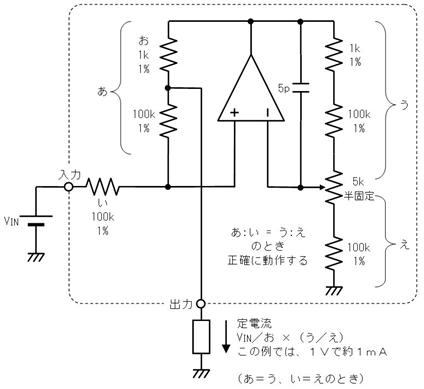
忋恾偺夞楬傕丄掞峈偺斾棪偑 偁丗偄亖偆丗偊
偺偲偒惓妋偵摦嶌偟丄弌椡揹棳偼乮偁亖偆丄偄亖偊偺応崌乯
弌椡揹棳亖乮擖椡揹埑亐偍乯亊乮偆亐偊乯
偱偡丅忋偺椺偱偼丄擖椡揹埑偑侾倁偺偲偒丄俤倶們倕倢偱=(1/1E3)*(100E3/100E3)偲寁嶼偟偰丄栺侾倣俙偱偡丅
偨偲偊偽僼僅僩僟僀僆乕僪偑敪惗偡傞揹棳乮岝揹棳乯偼丄恀拫偲埫埮偱侾枩攞埲忋曄壔偟傑偡丅偙偺偨傔丄應掕偵偼儗儞僕愗傝懼偊偑昁梫偱偡丅傑偨丄俙俢曄姺偟偰儅僀僐儞偵庢傝崬傓応崌傕丄價僢僩悢偺懡偄崅壙側俙俢俠偑昁梫偵側傝傑偡丅
偟偐偟丄壓恾偺夞楬偱岝揹棳傪張棟偡傞偲丄偙偺椺乮俀俶俁俋侽係傪巊梡乯偱偼丄岝揹棳偑侾侽攞偵側傞偛偲偵丄弌椡揹埑偑俇侽倣倁偢偮掅壓偡傞偨傔丄侽丏侾兪俙乣侾侽兪俙偺俀寘偺曄壔傪亅侽丏俇倁乣亅侽丏俈俀倁偺曄壔偵埑弅偱偒傑偡丅乮屻偵帵偡傛偆偵丄侾侽値俙乣侾侽兪俙偺俇寘偺曄壔偱偁偭偰傕丄亅侽丏俁俇倁乣乕侽丏俈俀倁偺曄壔偵埑弅偱偒傑偡乯
偙偺傛偆偵偟偰丄堦扷怣崋傪埑弅偟偰偟傑偊偽丄儗儞僕愗傝懼偊偑晄梫偵側傝傑偡偟丄價僢僩悢偺彮側偄俙俢俠偱傕儅僀僐儞偵庢傝崬傓偙偲偑偱偒傑偡丅
忋偵愢柧偟偨傛偆側丄悢寘偵傢偨偭偰曄壔偡傞擖椡傪乮椺偊偽丄侾侽攞偱俇侽倣倁偲偄偭偨婯懃偱乯埑弅偡傞夞楬傪乽儘僌傾儞僾乿偁傞偄偼乽懳悢埑弅夞楬乿偲屇傃傑偡丅
壓恾嵍懁偺懳悢埑弅夞楬偼丄壓恾塃懁偺僌儔僼偵帵偡傛偆偵乮椺偊偽俀俶俁俋侽係偱偼乯俬俠偑侾侽攞偵憹偊傞偲丄倁俛俤偑俇侽倣倁戝偒偔側傞尰徾傪棙梡偟偰偄傑偡丅乮俬俠偲倁俛俤偺娭學偼昳庬傗屄懱嵎偑偁傝傑偡乯
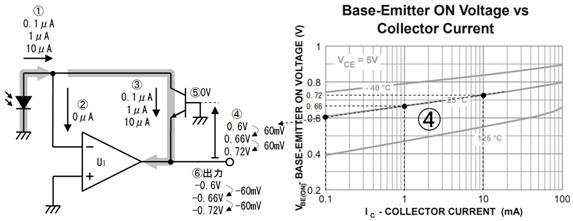
俈.侾. 妋擣
忋恾偺夞楬偺摦嶌傪丄壓昞偵彂偒崬傒側偑傜妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
抣
|
抣
|
|
嘆
|
僼僅僩僟僀僆乕僪偺岝揹棳偑
侽丏侾兪俙乣侾侽兪俙傑偱
侾侽侽攞曄壔偟偨応崌傪峫偊傑偡丅
|
侽丏侾倣俙
|
侾倣俙
|
侾侽倣俙
|
|
嘇
|
亅擖椡偵棳傟傞揹棳偼丄
|
倣俙
|
倣俙
|
倣俙
|
|
嘊
|
僐儗僋僞揹棳俬俠偼丄
乮忋恾塃偺僌儔僼偐傜丄乯
|
倣俙
|
倣俙
|
倣俙
|
|
嘋
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
|
倁
|
倁
|
倁
|
|
嘍
|
儀乕僗揹埑倁俛偼丄
|
倁
|
倁
|
倁
|
|
嘐
|
弌椡揹埑倁俷偼丄
|
倁
|
倁
|
倁
|
俈.俀. 摎
|
斣崋
|
幙栤
|
抣
|
抣
|
抣
|
|
嘆
|
僼僅僩僟僀僆乕僪偺岝揹棳偑
侽丏侾兪俙乣侾侽兪俙傑偱
侾侽侽攞曄壔偟偨応崌傪峫偊傑偡丅
|
侽丏侾倣俙
|
侾倣俙
|
侾侽倣俙
|
|
嘇
|
亅擖椡偵棳傟傞揹棳偼丄
|
侽倣俙
|
侽倣俙
|
侽倣俙
|
|
嘊
|
僐儗僋僞揹棳俬俠偼丄
乮忋恾塃偺僌儔僼偐傜丄乯
|
侽丏侾倣俙
|
侾倣俙
|
侾侽倣俙
|
|
嘋
|
儀乕僗僄儈僢僞娫揹埑倁俛俤偼丄
|
侽丏俇倁
|
侽丏俇俇倁
|
侽丏俈俀倁
|
|
嘍
|
儀乕僗揹埑倁俛偼丄
|
侽倁
|
侽倁
|
侽倁
|
|
嘐
|
弌椡揹埑倁俷偼丄
|
亅侽丏俇倁
|
亅侽丏俇俇倁
|
亅侽丏俈俀倁
|
忋恾塃偺僌儔僼偵偼婰嵹偝傟偰偄傑偣傫偑丄嵍懁偵墑挿偟偰傕摿惈偼捈慄偺傑傑乮俇侽倣倁偱侾侽攞偺忬懺傪曐偭偰乯懕偄偰偄傑偡丅偱偡偐傜壓昞偺傛偆偵丄偝傜偵峀偄斖埻偺揹棳偱懳悢埑弅傪峴偆偙偲偑偱偒傑偡丅
|
擖椡揹棳
乮俬俠乯
|
弌椡揹埑
乮倁俛俤乯
|
|
侾侽値俙
|
亅侽丏俁俇倁
|
|
侾侽侽値俙
|
亅侽丏係俀倁
|
|
侾兪俙
|
亅侽丏係俉
|
|
侾侽兪俙
|
亅侽丏俆係倁
|
|
侾侽侽兪俙
|
亅侽丏俇倁
|
|
侾倣俙
|
亅侽丏俇俇倁
|
|
侾侽倣俙
|
亅侽丏俈俀倁
|
偙偺傛偆偵戝曄曋棙側懳悢埑弅夞楬偱偡偑丄忋恾偺婎杮夞楬偺傑傑偱偼丄乮倁俛俤偑壏搙偱曄壔偡傞偨傔乯壏搙偱弌椡揹埑偑戝偒偔曄壔偟偰偟傑偄傑偡丅壓恾偼婛偵宖嵹偟偨俬俠亅倁俛俤偺僌儔僼偱偡丅
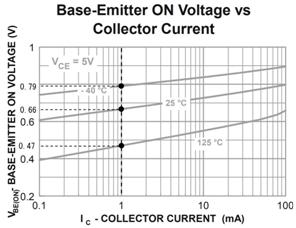
忋恾偐傜丄僐儗僋僞揱桪夒侾倣俙偱偁偭偰傕丄壏搙偑亅係侽亷丄俀俆亷丄侾俀俆亷丄偲曄壔偡傞偲丄倁俛俤偑丄侽丏俈俋倁丄侽丏俇俇倁丄侽丏係俈倁丄偲戝偒偔曄壔偡傞偙偲偑暘偐傝傑偡丅偦偙偱壓恾偺傛偆偵丄壏搙偺塭嬁傪懪偪徚偡岺晇傪偟傑偡丅
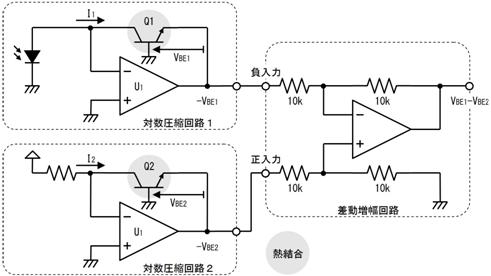
忋恾偱偼丄懳悢埑弅夞楬侾偼倁俛俤侾傪弌椡偟丄懳悢埑弅夞楬俀偼倁俛俤俀傪弌椡偟傑偡丅倁俛俤侾傕倁俛俤俀傕乮婛偵愢柧偟偨傛偆偵乯壏搙偱曄壔偟傑偡丅偦偙偱丄嵎摦憹暆夞楬偱倁俛俤侾偲倁俛俤俀偺嵎傪媮傔偰弌椡偟傑偡丅偙偙偱俻侾偲俻俀傪擬寢崌偟偰乮摨偠壏搙偵曐偭偰乯偍偔偲丄乮婥壏偑曄壔偟偰傕乯倁俛俤侾偲倁俛俤俀偑摨偠曄壔傪偟傑偡偐傜丄椉幰偺嵎傪媮傔偨弌椡揹埑偼壏搙偺塭嬁傪杦偳庴偗側偔側傝傑偡丅
偦偺偆偊偱丄懳悢埑弅夞楬侾偵偩偗擖椡揹棳俬侾傪擖椡偟丄懳悢埑弅夞楬俀偵偼忢偵堦掕偺揹棳俬俀傪擖椡偟傑偡丅偙傟偵傛偭偰丄嵎摦憹暆夞楬偺弌椡偵偼丄擖椡揹棳俬侾偵懳墳偟偨揹埑偑弌椡偝傟傑偡丅
偙偺傛偆偵丄擖椡偵懳墳偟偨倁俛俤偐傜婎弨偺倁俛俤傪堷偔曽朄乮嵎傪媮傔傞曽朄乯偱丄倁俛俤偺壏搙曄壔偑弌椡偵梌偊傞塭嬁傪偐側傝彫偝偔偱偒傑偡丅弌椡揹埑偑壏搙偱侾侽乣俀侽亾曄壔偟偰傕婥偵側傜側偄応崌偼丄偙偺曽朄偑棙梡偱偒傑偡丅
偝偰丄忋婰偺乽嵎傪媮傔傞曽朄乿偱傕懡彮偺壏搙曄壔偑惗偠傞棟桼偼丄忋恾偺僌儔僼偺孹偒偑丄壏搙偑崅偄掱戝偒偔側傞偨傔偱偡丅偙偺偨傔丄弌椡揹埑偼愨懳壏搙偵斾椺偟偰曄壔偟傑偡丅偨偲偊偽丄愨懳壏搙俁侽侽搙俲乮俀俈亷乯偱侾侽倁偑弌椡偝傟偰偄傞偲偒丄愨懳壏搙偑俁俁侽搙俲乮俆俈亷乯偵忋徃偡傞偲丄侾侾倁偑弌椡偝傟傑偡丅
偦偙偱丄壓恾偺傛偆偵丄俁侽亷偱侾侽亾掞峈抣偑崅偔側傞掞峈乮壏搙學悢俁俁侽侽倫倫倣乛亷偺掞峈乯傪巊偭偰壏搙偵傛傞弌椡偺曄壔傪懪偪徚偟傑偡丅
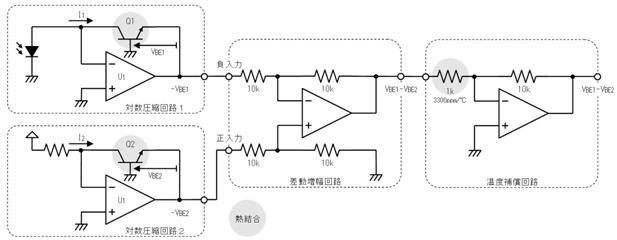
忋恾偺夞楬偱偼僆儁傾儞僾偺巊梡屄悢偑懡偄偱偡偟丄乮崱偼杦偳斕攧偝傟偰偄傑偣傫偑乯俀偮偺摿惈偺懙偭偨僩儔儞僕僗僞傪侾偮偺僷僢働乕僕偵擖傟偨乽僨儏傾儖僩儔儞僕僗僞乿偼俀偮偺僩儔儞僕僗僞偺僄儈僢僞偑宷偑偭偰偄傞応崌偑懡偄偨傔丄壓恾偺傛偆偵岺晇偟偨夞楬偑椙偔巊傢傟傑偡丅壓恾偺夞楬偼偐側傝嬅偭偨峔惉偵側偭偰偄傑偡偐傜丄捈偪偵棟夝偱偒側偔偰傕栤戣偁傝傑偣傫丅
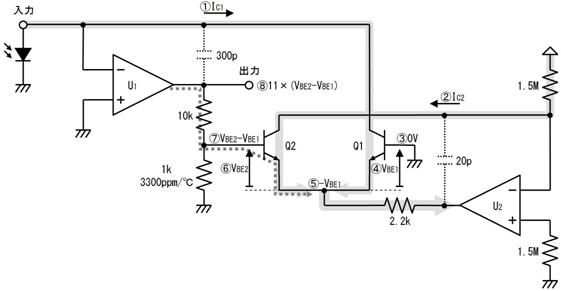
忋恾偺夞楬偱偼丄倀侾偼俻俀傪僄儈僢僞僼僅儘傾偺傛偆偵摦嶌偝偣偰俻侾偺僄儈僢僞揹埑傪惂屼偟丄俻侾偵擖椡揹棳嘆俬俠侾傪棳偟偰嘋倁俛俤侾傪敪惗偝偣傑偡乮偮傑傝丄倀侾偺擖椡揹棳俬俠侾偵偼倁俛俤侾偑懳墳偟傑偡乯丅倀俀偼俻俀偺僄儈僢僞傪惂屼偟偰丄堦掕偺揹棳嘇俬俠俀傪棳偟傑偡乮偮傑傝丄倀俀偺擖椡揹棳俬俀偵偼倁俛俤俀偑懳墳偟傑偡乯丅
俈.俁. 妋擣
忋恾偺夞楬偺弌椡揹埑傪丄壓昞偵婰擖偟偰妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡偐傜棳傟崬傓揹棳傪侾俠侾偲偟傑偡丅
|
亅
|
|
嘇
|
掞峈偐傜棳傟崬傓堦掕偺揹棳傪侾俠俀偲偟傑偡丅
|
亅
|
|
嘊
|
俻侾偺儀乕僗揹埑偼丄
乮傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
倁
|
|
嘋
|
俻侾偺倁俛俤偼俬俠侾偵懳墳偟偨倁俛俤侾偱偡丅
|
亅
|
|
嘍
|
俻俀偺僄儈僢僞揹埑偼丄乮慖傫偱壓偝偄乯
乮嘊偲嘋偐傜丄乯
|
亅倁俛俤俀
亅倁俛俤侾
|
|
嘐
|
俻俀偺倁俛俤偼俬俠俀偵懳墳偟偨倁俛俤俀偱偡丅
|
亅
|
|
嘑
|
俻俀偺儀乕僗揹埑偼丄乮慖傫偱壓偝偄乯
乮嘍偲嘐偐傜丄乯
|
倁俛俤侾亅倁俛俤俀
倁俛俤俀亅倁俛俤侾
|
|
嘒
|
弌椡抂巕偺揹埑偼丄乮慖傫偱壓偝偄乯
乮侾侽倠偲侾倠偐傜丄乯
|
侾侾亊倁俛俤俀亅倁俛俤侾
侾侾亊倁俛俤俀亅倁俛俤侾
|
俈.係. 摎
|
斣崋
|
幙栤
|
抣
|
|
嘆
|
擖椡偐傜棳傟崬傓揹棳傪侾俠侾偲偟傑偡丅
|
亅
|
|
嘇
|
掞峈偐傜棳傟崬傓堦掕偺揹棳傪侾俠俀偲偟傑偡丅
|
亅
|
|
嘊
|
俻侾偺儀乕僗揹埑偼丄
乮傾乕僗偵愙懕偝傟偰偄傞偐傜丄乯
|
侽倁
|
|
嘋
|
俻侾偺倁俛俤偼俬俠侾偵懳墳偟偨倁俛俤侾偱偡丅
|
亅
|
|
嘍
|
俻俀偺僄儈僢僞揹埑偼丄乮慖傫偱壓偝偄乯
乮嘊偲嘋偐傜丄乯
|
亅倁俛俤俀
亅倁俛俤侾
|
|
嘐
|
俻俀偺倁俛俤偼俬俠俀偵懳墳偟偨倁俛俤俀偱偡丅
|
亅
|
|
嘑
|
俻俀偺儀乕僗揹埑偼丄乮慖傫偱壓偝偄乯
乮嘍偲嘐偐傜丄乯
|
倁俛俤侾亅倁俛俤俀
倁俛俤俀亅倁俛俤侾
|
|
嘒
|
弌椡抂巕偺揹埑偼丄乮慖傫偱壓偝偄乯
乮侾侽倠偲侾倠偐傜丄乯
|
侾侾亊倁俛俤俀亅倁俛俤侾
侾侾亊倁俛俤俀亅倁俛俤侾
|
偙偺傛偆偵弌椡偵偼俀偮偺倁俛俤偺嵎偑弌椡偝傟傑偡丅傑偨丄俻俀偺儀乕僗偵愙懕偝傟偨亄俁俁侽侽倫倫倣乛亷乮亄侽丏俁亾乛亷乯偺掞峈偱愨懳壏搙偵斾椺偟偨弌椡揹埑偺忋徃傕杊偄偱偄傑偡丅俻侾丄俻俀丄侾倠兌偼擬寢崌偟偰偍偒傑偡丅
僨儏傾儖僩儔儞僕僗僞偼崱傗擖庤偑崲擄偵側偭偰偄傑偡偐傜丄俀偮偺僩儔儞僕僗僞傪枾拝偟偰愙拝乮曄惈僔儕僐乕儞愙拝嵻摍乯偟丄傾儖儈傗摵敁偺擲拝僥乕僾傪姫偒偮偗偰擬寢崌偟傑偡丅
偙偺夞楬偵乮僼僅僩僟僀僆乕僪摍傪愙懕偟偰乯揹棳傪擖椡偡傞偺偱偼側偔丄揹埑傪擖椡偡傞応崌偼丄壓恾偵帵偡傛偆偵丄倀侾偺擖椡偵掞峈傪捛壛偟傑偡丅
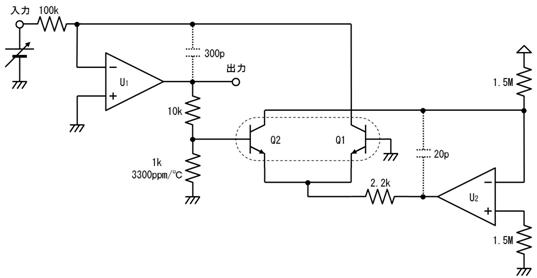
壓恾偺夞楬傪巊梡偟偰丄懳悢埑弅偟偨揹埑傪尦偺揹埑偵栠偡偙偲傕偱偒傑偡丅偙偺傛偆側夞楬傪傾儞僠儘僌傾儞僾乮媡懳悢憹暆婍乯偲屇傃傑偡丅
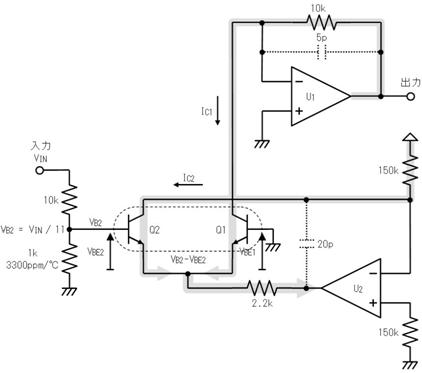
忋恾偺倀俀偼丄堦掕偺僐儗僋僞揹棳俬俠俀傪俻俀偵棳偟偰丄堦掕偺倁俛俤俀傪敪惗偝偣傑偡丅擖椡揹埑偼侾侽倠兌偲侾倠兌偱暘埑偝傟偰俻俀偺儀乕僗偵壛偊傜傟丄偦偺寢壥俻俀偺僄儈僢僞偼倁俛俀乮暘埑偝傟偨擖椡揹埑乯傛傝丄倁俛俤俀偩偗掅偄揹埑偵側傝傑偡丅俻侾偼儀乕僗偑愙抧偝傟偰偄傞偨傔丄俻俀偺僄儈僢僞揹埑乮倁俛俀亅倁俛俤俀乯偵懳墳偟偨僐儗僋僞揹棳俬俠侾偑棳傟傑偡丅倀侾偼俬俠侾傪侾侽倠兌偱揹埑偵曄姺偟偰弌椡偟傑偡丅
偝偰丄偙偙傑偱愢柧偟偨懳悢埑弅夞楬偱偼丄僩儔儞僕僗僞偺俬俠乗倁俛俤摿惈偵懳悢偺娭學偑偁傞偙偲傪棙梡偟傑偟偨丅偲偙傠偱壓恾偵帵偡傛偆偵丄僟僀僆乕僪偺俬俥乗倁俥偵傕乮僩儔儞僕僗僞偲摨條偺乯懳悢偺娭學偑偁傝傑偡乮侾俶係侾係俉偺椺乯丅僌儔僼偐傜丄峀偄俬俥偺斖埻偱丄俬俥偑侾侽攞偵側傞偲偛偲偵丄倁俥偑栺侾俀侽倣倁偢偮忋徃偡傞偲偄偆娭學偑堐帩偝傟偰偄傞偙偲偑暘偐傝傑偡丅
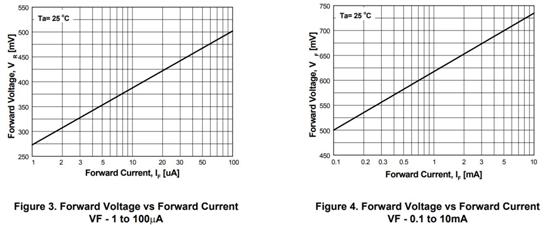
偙偺偨傔壓恾乮倎乯偺傛偆偵僟僀僆乕僪傪巊梡偟偨夞楬偱懳悢埑弅傪峴偆偙偲傕偱偒傑偡丅偟偐偟丄僟僀僆乕僪傪巊偭偨夞楬偵偼師偺傛偆側庛揰偑偁傝傑偡丅
偮傑傝丄僩儔儞僕僗僞傪巊梡偟偨夞楬乮倐乯偱偼丄儀乕僗偑傾乕僗偵愙懕偝傟偰偄傞偨傔丄僆儁傾儞僾偺僆僼僙僢僩揹埑偵娭學側偔丄惓妋偵倁俛俤偑弌椡偝傟傑偟偨丅偟偐偟丄僟僀僆乕僪傪巊偭偨夞楬偱偼丄僆儁傾儞僾偺擖椡僆僼僙僢僩揹埑偑弌椡偵尰傟偰偟傑偄傑偡丅
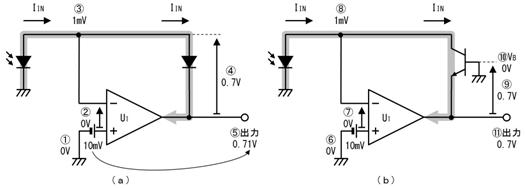
俈.俆. 妋擣
忋恾乮倎乯乮倐乯偺奺夞楬偱丄僆僼僙僢僩揹埑偺塭嬁傪妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
抣
|
|
|
乮倎乯偺夞楬偵偮偄偰峫偊傑偡丅
僆儁傾儞僾偵僆僼僙僢僩揹埑偑侾侽倣倁偁傞偲偟傑偡丅
|
亅
|
|
嘆
|
亄擖椡偺揹埑偼丄乮僆僼僙僢僩揹埑偺塭嬁傪峫偊偰丄乯
|
倣倁
|
|
嘇
|
亄擖椡偲亅揹埑偺揹埑嵎偼丄
乮僟僀僆乕僪偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
倁
|
|
嘊
|
亅擖椡偺揹埑偼丄
|
倣倁
|
|
嘋
|
僟僀僆乕僪偺椉抂揹埑傪侽丏俈倁偲偟傑偡丅
|
亅
|
|
嘍
|
弌椡揹埑偼丄
乮嘊偲嘋偐傜丄乯
|
倁
|
|
|
乮倐乯偺夞楬偵偮偄偰峫偊傑偡丅
僆儁傾儞僾偵僆僼僙僢僩揹埑偑侾侽倣倁偁傞偲偟傑偡丅
|
亅
|
|
嘐
|
亄擖椡偺揹埑偼丄乮僆僼僙僢僩揹埑偺塭嬁傪峫偊偰丄乯
|
倣倁
|
|
嘑
|
亄擖椡偲亅揹埑偺揹埑嵎偼丄
乮僩儔儞僕僗僞偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
倁
|
|
嘒
|
亅擖椡偺揹埑偼丄
|
倣倁
|
|
嘓
|
僩儔儞僕僗僞偺倁俛俤傪侽丏俈倁偲偟傑偡丅
|
|
|
嘔
|
儀乕僗揹埑偼丄
|
倁
|
|
嘕
|
弌椡揹埑偼丄
乮嘓偲嘔偐傜丄乯
|
倁
|
俈.俇. 摎
|
斣崋
|
幙栤
|
抣
|
|
|
乮倎乯偺夞楬偵偮偄偰峫偊傑偡丅
僆儁傾儞僾偵僆僼僙僢僩揹埑偑侾侽倣倁偁傞偲偟傑偡丅
|
亅
|
|
嘆
|
亄擖椡偺揹埑偼丄乮僆僼僙僢僩揹埑偺塭嬁傪峫偊偰丄乯
|
侾侽倣倁
|
|
嘇
|
亄擖椡偲亅揹埑偺揹埑嵎偼丄
乮僟僀僆乕僪偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
侽倁
|
|
嘊
|
亅擖椡偺揹埑偼丄
|
侾倣倁
|
|
嘋
|
僟僀僆乕僪偺椉抂揹埑傪侽丏俈倁偲偟傑偡丅
|
亅
|
|
嘍
|
弌椡揹埑偼丄
乮嘊偲嘋偐傜丄乯
|
侽丏俈侾倁
|
|
|
乮倐乯偺夞楬偵偮偄偰峫偊傑偡丅
僆儁傾儞僾偵僆僼僙僢僩揹埑偑侾侽倣倁偁傞偲偟傑偡丅
|
亅
|
|
嘐
|
亄擖椡偺揹埑偼丄乮僆僼僙僢僩揹埑偺塭嬁傪峫偊偰丄乯
|
侾侽倣倁
|
|
嘑
|
亄擖椡偲亅揹埑偺揹埑嵎偼丄
乮僩儔儞僕僗僞偱晧婣娨偑妡偐偭偰偄傞偐傜丄乯
|
侽倁
|
|
嘒
|
亅擖椡偺揹埑偼丄
|
侾倣倁
|
|
嘓
|
僩儔儞僕僗僞偺倁俛俤傪侽丏俈倁偲偟傑偡丅
|
|
|
嘔
|
儀乕僗揹埑偼丄
|
侽倁
|
|
嘕
|
弌椡揹埑偼丄
乮嘓偲嘔偐傜丄乯
|
侽丏俈倁
|
偙偺傛偆偵揹棳傪弌椡偡傞乮僼僅僩僟僀僆乕僪偺傛偆側乯慺巕傪擖椡偵愙懕偟偰乽揹棳傪擖椡乿偟偰巊梡偡傞応崌偼丄乮僆儁傾儞僾偺僆僼僙僢僩揹埑偺塭嬁傪夞旔偱偒傞偺偱乯僩儔儞僕僗僞傪梡偄偨夞楬偑桳棙偱偡丅
媡偵丄擖椡偵掞峈傪捛壛偟偰乽揹埑傪擖椡乿偟偰巊梡偡傞応崌偼丄僩儔儞僕僗僞傪梡偄偰傕僆僼僙僢僩揹埑偺塭嬁偑乮擖椡懁偱乯敪惗偟傑偡偐傜丄僟僀僆乕僪傪梡偄偨夞楬偱傕偝傎偳晄棙偱偼偁傝傑偣傫丅偨偩偟丄壏搙偺塭嬁傪柍偔偡偨傔偵俀偮偺倁俥偺嵎傪媮傔偰丄偝傜偵愨懳壏搙偺曗彏傪峴偆偲側傞偲丄壓恾偺傛偆偵堄奜偲暋嶨側夞楬偲側傝丄媡偵僩儔儞僕僗僞傪巊偭偨夞楬偺曽偑娙扨偵側傝傑偡丅
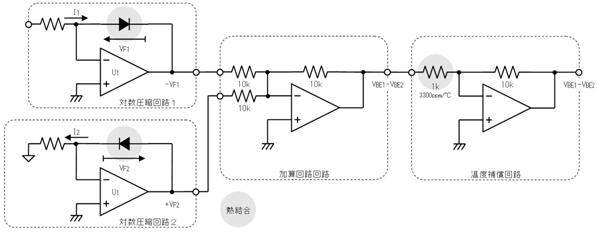
惓尫攇傪敪怳偡傞夞楬偼悢懡偔偁傝傑偡丅壓恾偼偦偺堦椺偱乽僂傿乕儞僽儕僢僕敪怳夞楬乿偲屇偽傟偰偄傑偡丅
壓恾乮倎乯偺僶儞僪僶僗僼傿儖僞偼拞怱廃攇悢偑栺侾倠俫倸偱丄侾倠俫倸偺怣崋偑俁暘偺侾偵庛傑傞摿惈傪帩偭偰偄傑偡丅偦偙偱丄僼傿儖僞偺弌椡傪壓恾乮倐乯偺憹暆夞楬偱俁攞偵憹暆偟偰尦偺怳暆偵栠偟丄嵞傃僼傿儖僞偵擖椡乮惓婣娨乯偟傑偡丅偙傟偵傛偭偰侾倠俫倸偺怣崋偑夞楬偺拞傪偄偮傑偱傕夞傝懕偗丄敪怳偟傑偡丅
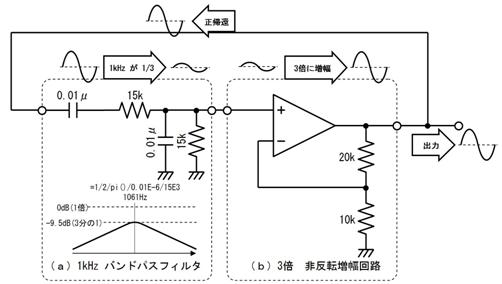
忋恾偺婎杮夞楬偼丄摨恾乮倐乯偺憹暆棪偑俁攞傛傝彮偟偱傕戝偒偄偲丄壓恾乮倎乯偺傛偆偵丄攇偼師戞偵戝偒偔側傝丄忋壓偑榗傫偱偟傑偄傑偡丅媡偵憹暆棪偑丄俁攞傛傝彮偟偱傕彫偝偄偲丄壓恾乮倐乯偺傛偆偵攇偑師戞偵彫偝偔側傝丄巭傑偭偰偟傑偄傑偡丅偱偡偐傜丄婘偺忋偵儃乕儖儁儞傪乮愭抂傪壓偵偟偰乯棫偰傞偺偑柍棟側偺偲摨條偵丄忋恾偺婎杮夞楬偱偼丄弌椡傪堦掕偺怳暆傪曐偮偙偲偼偱偒傑偣傫丅
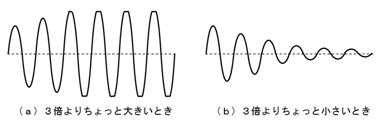
壓恾偺夞楬偼丄俁杮偺侾侽倠兌偱憹暆棪傪俁攞偵愝掕偟丄儃儕僂儉乮俆倠兌偐傜丄俆侽倠兌傑偱丄偄偢傟偺抣偱傕巊梡壜擻乯偲侾侽侽倠兌偱憹暆棪傪旝挷惍偱偒傞傛偆偵岺晇偟偰偄傑偡丅偟偐偟丄偨偲偊憹暆棪傪旝挷惍偟偰傕丄攇偼師戞偵戝偒偔側傝榗傓偐丄師戞偵彫偝偔側偭偰柍偔側傝傑偡丅偱偡偐傜丄壓恾偺夞楬偱偼丄掞峈偲暲楍偵僟僀僆乕僪傪愙懕偟偰偄傑偡丅弌椡怳暆偑戝偒偔側傞偲丄僟僀僆乕僪偵揹棳偑棳傟乮掞峈偑彫偝偔側偭偨偺偲帡偨岠壥傪惗偠偰乯憹暆棪偑壓偑傝丄戝偒偔榗傓偙偲傪杊偄偱偄傑偡丅
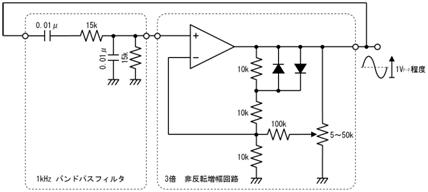
忋偺夞楬偱偼儃儕僂儉傪挷惍偡傞偲弌椡怳暆偑曄壔偟傑偡丅怳暆偑戝偒偄掱丄僟僀僆乕僪偑摫捠偟偰攇宍偑榗傒傑偡偐傜丄僟僀僆乕僪偵旝偐偵揹棳偑棳傟傞掱搙丄偮傑傝弌椡偑侾倁俹亅俹掱搙偵側傞傛偆丄儃儕僂儉傪挷惍偟傑偡丅
忋偺夞楬偺敪怳廃攇悢偼僶儞僪僷僗僼傿儖僞偺拞怱廃攇悢偱寛傑傝丄掞峈傪俼侾丄僐儞僨儞僒傪俠侾偲偡傟偽乮俀偮偺僐儞僨儞僒偲掞峈偼摨偠抣偵偟傑偡乯敪怳廃攇悢偼
=1/2/PI()/C1/R1
偱媮傔傞偙偲偑偱偒傑偡丅
廃攇悢傪壜曄偡傞応崌偼丄壓恾偺傛偆偵俀楢儃儕僂儉傪巊偄傑偡丅壓恾偺応崌廃攇悢傪侾丗侾侽掱搙偵壜曄偱偒傑偡丅僆儁傾儞僾偵俠俵俷俽僞僀僾傗俥俤俿擖椡僞僀僾傪巊梡偡傟偽丄俀楢儃儕僂儉偵侾侽侽倠兌偺昳庬傪巊梡偟偰丄廃攇悢傪侾侽侽攞壜曄偡傞偙偲傕偱偒傑偡丅
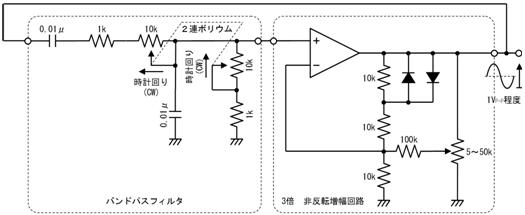
俀楢儃儕僂儉偱廃攇悢傪戝偒偔壜曄偟偨偲偒丄乮俀楢儃儕僂儉傗僐儞僨儞僒偺惈擻偵傛偭偰偼乯夞楬恾塃懁偺儃儕僂儉乮俆乣俆侽倠兌乯傕丄懡彮挷愡偡傞昁梫偑惗偠傞応崌偑偁傝傑偡丅
壓恾偺夞楬偼乽僼傽儞僋僔儑儞僛僱儗乕僞乿偲屇偽傟丄嶰妏攇偲嬮宍攇傪摨帪偵敪惗偱偒傑偡丅愊暘夞楬偲旕斀揮僔儏儈僢僩僩儕僈傪愙懕偟偨夞楬偱偡丅
僼傽儞僋僔儑儞僛僱儗乕僞偼丄婛偵楙廗偟偨乽柍埨掕儅儖僠僶僀僽儗乕僞乿偺俠俼愊暘夞楬偺戙傝偵丄僆儁傾儞僾偵傛傞愊暘夞楬傪巊梡偟偰偄傞偨傔丄鉟楉側嶰妏攇偑弌椡偝傟傑偡丅摦嶌偺巇慻傒偼柍埨掕儅儖僠僶僀僽儗乕僞偲椙偔帡偰偄傑偡丅
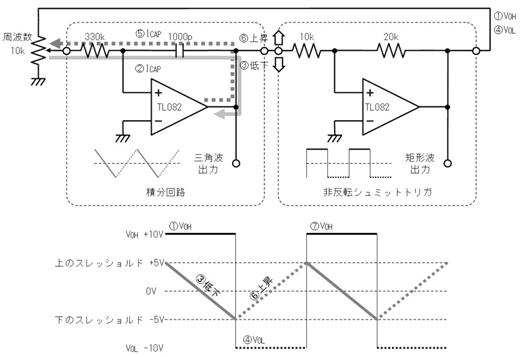
俋.侾. 妋擣
忋恾傪嶲峫偵壓昞偺慖戰巿傪慖傃側偑傜僼傽儞僋僔儑儞僛僱儗乕僞偺摦嶌傪妋擣偟偰偔偩偝偄丅
|
斣崋
|
幙栤
|
慖戰巿
|
|
嘆
|
旕斀揮僔儏儈僢僩僩儕僈偼倁俷俫乮侾侽倁乯傪弌椡偟偰偄傞偲偟傑偡丅
|
乕
|
|
嘇
|
僔儏儈僢僩僩儕僈偺弌椡偑愊暘夞楬偵擖椡偝傟偰偄傞偐傜丄偙偺偲偒愊暘夞楬偺僐儞僨儞僒偵棳傟傞揹棳偺岦偒偼丄
|
塃岦偒
嵍岦偒
|
|
嘊
|
忋偺嘇偺岦偒偵揹棳偑棳傟傞偨傔丄愊暘婍偺弌椡揹埑偼丄
|
忋徃
掅壓
|
|
嘋
|
愊暘婍偺弌椡偑壓偺僗儗僢僔儑儖僪偵払偡傞偲丄旕斀揮僔儏儈僢僩僩儕僈偺弌椡偼丄
|
倁俷俫偵斀揮
倁俷俴偵斀揮
|
|
嘍
|
愊暘夞楬偺僐儞僨儞僒偵棳傟傞揹棳偺岦偒偼丄
乮僔儏儈僢僩僩儕僈偺弌椡偑愊暘夞楬偵擖椡偝傟偰偄傞偐傜丄乯
|
塃岦偒
嵍岦偒
|
|
嘐
|
忋偺嘇偺岦偒偵揹棳偑棳傟傞偨傔丄愊暘婍偺弌椡揹埑偼丄
|
忋徃
掅壓
|
|
嘑
|
愊暘婍偺弌椡偑忋偺僗儗僢僔儑儖僪偵払偡傞偲丄旕斀揮僔儏儈僢僩僩儕僈偺弌椡偼丄
|
倁俷俫偵斀揮
倁俷俴偵斀揮
|
|
嘒
|
偙偺傛偆偵偟偰丄嵞傃嘆偺忬懺偵栠偭偰孞傝曉偟傑偡丅
|
乕
|
俋.俀. 摎
|
斣崋
|
幙栤
|
慖戰巿
|
|
嘆
|
旕斀揮僔儏儈僢僩僩儕僈偼倁俷俫乮侾侽倁乯傪弌椡偟偰偄傞偲偟傑偡丅
|
乕
|
|
嘇
|
僔儏儈僢僩僩儕僈偺弌椡偑愊暘夞楬偵擖椡偝傟偰偄傞偐傜丄偙偺偲偒愊暘夞楬偺僐儞僨儞僒偵棳傟傞揹棳偺岦偒偼丄
|
塃岦偒
嵍岦偒
|
|
嘊
|
忋偺嘇偺岦偒偵揹棳偑棳傟傞偨傔丄愊暘婍偺弌椡揹埑偼丄
|
忋徃
掅壓
|
|
嘋
|
愊暘婍偺弌椡偑壓偺僗儗僢僔儑儖僪偵払偡傞偲丄旕斀揮僔儏儈僢僩僩儕僈偺弌椡偼丄
|
倁俷俫偵斀揮
倁俷俴偵斀揮
|
|
嘍
|
愊暘夞楬偺僐儞僨儞僒偵棳傟傞揹棳偺岦偒偼丄
乮僔儏儈僢僩僩儕僈偺弌椡偑愊暘夞楬偵擖椡偝傟偰偄傞偐傜丄乯
|
塃岦偒
嵍岦偒
|
|
嘐
|
忋偺嘇偺岦偒偵揹棳偑棳傟傞偨傔丄愊暘婍偺弌椡揹埑偼丄
|
忋徃
掅壓
|
|
嘑
|
愊暘婍偺弌椡偑忋偺僗儗僢僔儑儖僪偵払偡傞偲丄旕斀揮僔儏儈僢僩僩儕僈偺弌椡偼丄
|
倁俷俫偵斀揮
倁俷俴偵斀揮
|
|
嘒
|
偙偺傛偆偵偟偰丄嵞傃嘆偺忬懺偵栠偭偰孞傝曉偟傑偡丅
|
乕
|
僼傽儞僋僔儑儞僛僱儗乕僞偺敪怳廃攇悢偼丄弌椡偑掅壓偡傞偺偵昁梫側帪娫偲丄弌椡偑忋徃偡傞偺偵昁梫側帪娫傪媮傔丄椉幰傪崌寁偟偰廃婜傪媮傔偰寁嶼偟傑偡丅
傑偢丄弌椡偑掅壓偡傞偺偵昁梫側帪娫偼丄儃儕僂儉傪嵟戝乮嵟傕崅偄廃攇悢乯偵愝掕偟偨応崌丄崱夞椺偺傛偆偵丄忋偺僗儗僢僔儑儖僪偲壓偺僗儗僢僔儑儖僪偺嵎乮倁俫倄乯偑侾侽倁側傜丄
弌椡偑掅壓偡傞偺偵昁梫側帪娫
亖 侾侽倁
亊 俁俁侽倠
亊 侾侽侽侽倫
乛 倁俷俫
俤倶們倕倢偱丄=10*330E3*1000E-12/10偲寁嶼偟偰丄侽丏俁俁倣昩
乮亖
倁俫倄 亊 俼俬俶
亊 俠俥 乛
倁俷俫乯
摨條偵
弌椡偑忋徃偡傞偺偵昁梫側帪娫
亖 侾侽倁
亊 俁俁侽倠
亊 侾侽侽侽倫
乛 倁俷俴
俤倶們倕倢偱丄=10*330E3*1000E-12/10偲寁嶼偟偰丄侽丏俁俁倣昩
乮亖
倁俫倄 亊 俼俬俶
亊 俠俥 乛
倁俷俴乯
偲寁嶼偡傞偙偲偑偱偒傑偡丅偱偡偐傜乮儃儕僂儉傪嵟戝偵偟偨応崌偺乯敪怳廃婜偼侽丏俇俇倣昩偱廃攇悢偼丄侾俆侽侽俫倸偲暘偐傝傑偡丅掅壓帪娫偲忋徃帪娫偼摨偠側偺偱丄師偺傛偆偵寁嶼偡傞偙偲傕偱偒傑偡丅
敪怳廃攇悢
亖 倁俷俫
乛 俀 乛 倁俫倄 乛 俼俬俶
乛 俠俥
壓恾偺傛偆偵僼傽儞僋僔儑儞僛僱儗乕僞偺夞楬傪夵憿偡傞偲丄嫎帟忬攇傪敪惗偝偣傞偙偲偑偱偒傑偡丅
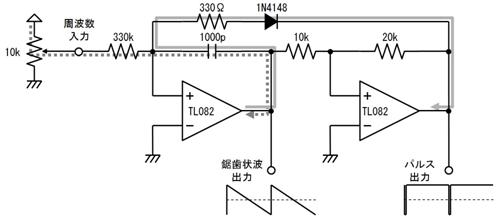
忋恾偺夞楬偱丄旕斀揮僔儏儈僢僩僩儕僈偑倁俷俴傪弌椡偡傞偲丄僟僀僆乕僪偑乮弴揹埑偱乯摫捠偟偰丄奃怓懢慄偱帵偡宱楬偱俁俁侽兌傪捠偠偰戝偒側揹棳偑棳傟丄堦弖偱愊暘婍偺弌椡偑忋徃偟偰丄僔儏儈僢僩僩儕僈偼倁俷俫偵斀揮偟傑偡丅
僔儏儈僢僩僩儕僈偑倁俷俫傪弌椡偡傞偲丄僟僀僆乕僪偼乮媡揹埑偱乯揹棳傪棳偝側偔側傝丄奃怓揰慄偱帵偡宱楬偱丄俁俁侽倠兌傪捠偠偰棳傟傞嬐偐側揹棳偱丄備偭偔傝偲愊暘婍偺弌椡偑掅壓偟偰峴偒傑偡丅愊暘婍偺弌椡偑壓偺僗儗僢僔儑儖僪偵払偡傞偲丄僔儏儈僢僩僩儕僈偼嵞傃倁俷俴傪弌椡偟傑偡丅
偙傟傪孞傝曉偟偰丄慺憗偔忋徃偟丄備偭偔傝偲掅壓偡傞嫎帟忬攇偑弌椡偝傟傑偡丅偙偺敪怳夞楬偼丄擖椡抂巕偺揹埑偱廃攇悢傪峀斖埻偵壜曄偱偒傞摿挜傕偁傝傑偡丅
敪怳廃攇悢偼師偺傛偆偵寁嶼偱偒傑偡丅
敪怳廃攇悢 亖 擖椡揹埑 乛 俀偮偺僗儗僢僔儑儖僪揹埑偺嵎 乛 擖椡掞峈 乛 愊暘僐儞僨儞僒
亖
倁俬俶 乛 倁俫倄
乛 俼俬俶 乛
俠俥
椺偊偽侾倁傪擖椡偟偨応崌偼丄
亖
侾倁 乛 侾侽倁 乛 俁俁侽倠
乛 侾侽侽侽倫
俤倶們倕倢偱 =1/10/330E3/1000E-12 偲擖椡偟偰丄俁侽俁俫倸偲寁嶼偱偒傑偡丅侾侽倁傪擖椡偡傞偲丄俁侽俁侽俫倸偱敪怳偟傑偡丅偙偺傛偆偵揹埑偱敪怳廃攇悢傪曄峏偱偒傞敪怣婡傪乽揹埑惂屼敪怳婍乮倁俠俷乯乿偲屇傃傑偡丅
僷儖僗偺暆偼壓恾偵帵偡傛偆偵丄僨儏乕僥傿僒僀僋儖乮侾廃婜偺拞偱丄揹埑偑崅偄乮俫丗僴僀乯婜娫偺妱崌乯偱昞偟傑偡丅僨儏乕僥傿僒僀僋儖偑俀侽亾側傜丄壓恾乮倎乯偵帵偡傛偆偵丄侾廃婜拞偺俀侽亾偑俫偺婜娫偱丄俆侽亾側傜丄壓恾乮倐乯偵帵偡傛偆偵丄侾廃婜拞偺敿暘偑俫偺婜娫偱偡丅
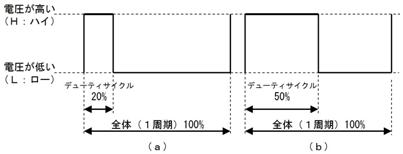
僷儖僗暆曄挷乮俹倂俵乯夞楬偲偼丄廃攇悢傪曄偊偢偵僷儖僗偺暆偩偗傪曄峏偡傞夞楬偱偡丅壓恾忋懁偼偡偱偵愢柧偟偨嶰妏攇敪惗夞楬偱丄摨恾壓懁偵揰慄偱埻偭偰帵偡晹暘偑僷儖僗暆曄挷夞楬偱偡丅
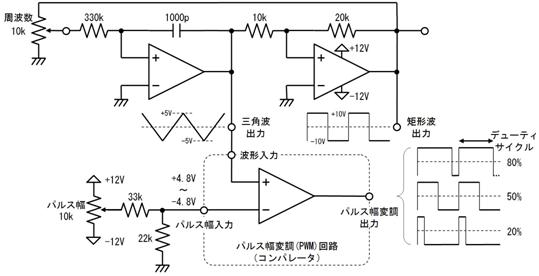
僷儖僗暆曄挷夞楬偺惓懱偼丄乽僷儖僗暆擖椡乿偲乽攇宍擖椡乿傪斾妑偡傞僐儞僷儗乕僞偱丄壓恾偵帵偡傛偆偵丄嶰妏攇偑僷儖僗暆擖椡揹埑傛傝崅偄偲偒偼俫傪丄掅偄偲偒偼俴傪弌椡偟傑偡丅

壓恾乮倎乯偺傛偆偵丄僷儖僗暆擖椡偺揹埑偑丄嶰妏攇偺嵟掅揹埑傛傝掅偄丄偁傞偄偼丄乮倐乯偺傛偆偵丄嶰妏攇偺嵟崅揹埑傛傝崅偄応崌偼丄僷儖僗偑弌椡偝傟傑偣傫丅偱偡偐傜丄忢偵僷儖僗偑弌傞傛偆偵偟偨偄応崌偼丄僷儖僗暆擖椡抂巕偵壛偊傞揹埑傪丄嶰妏攇偺嵟掅揹埑乣嵟崅揹埑偲側傞傛偆偵偟傑偡丅

忋恾偺夞楬偼僐儞僷儗乕僞偺亄擖椡偲亅擖椡傪媡偵愙懕偟偰傕摦嶌偟傑偡丅偙偺応崌丄弌椡攇宍偺忋壓偑媡偵側傝傑偡丅

攇宍擖椡抂巕偵丄壓恾乮倎乯偺傛偆偵嶰妏攇偱偼側偔嫎帟忬攇傪壛偊偰傕摦嶌偟傑偡丅傑偨丄壓恾乮倐乯偺傛偆偵丄惓尫攇傪壛偊偰傕摦嶌偟傑偡偑丄偙偺応崌丄僷儖僗暆擖椡抂巕偺揹埑偲僨儏乕僥傿僒僀僋儖偑斾椺偟側偔側傝傑偡丅

侾係. 僼傿儖僞
婛偵愢柧偟偨侾師偺僼傿儖僞偺傛偆偵丄廃攇悢偵傛偭偰棙摼偑曄壔偡傞夞楬傪僼傿儖僞偲屇傃傑偡丅晄梫側廃攇悢偺怣崋傪庢傝彍偄偨傝丄婓朷偺怣崋偩偗傪慖戰偡傞側偳偺梡搑偱巊傢傟傑偡丅
僼傿儖僞偺嫵壢彂偵偼丄戲嶳偺庬椶偺夞楬傗丄僠僃價僠僃僼丄僶僞儚乕僗丄儀僢僙儖丄僈僂僔傾儞摍偺懡偔偺柤慜偲悢幃偑搊応偡傞忋丄撲傔偄偨僌儔僼傕懡偄偨傔丄僼傿儖僞偼擄偟偄偲巚偄彑偪偱偡丅
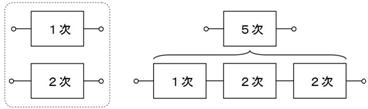
幚偼僼傿儖僞偵偼俀庬椶偟偐側偔丄偦偺俀庬椶偺愝掕偺慻傒崌傢偣偱條乆側僼傿儖僞偑偱偒偰偄傑偡丅偦偺俀偮偲偼丄忋恾嵍偺侾師偺僼傿儖僞偲丄俀師偺僼傿儖僞偱偡丅椺偊偽俆師偺僼傿儖僞偼丄忋恾塃懁偺傛偆偵丄侾師偺僼傿儖僞侾偮偲丄俀師偺僼傿儖僞傪俀偮傪宷偄偩傕偺偱偡丅
偙偙偱尵偆乽侾師偺僼傿儖僞乿偼丄婛偵侾師偺僼傿儖僞偺崁偱庢傝忋偘偨乽慻傒崌傢偣僼傿儖僞乿偺傛偆側暋嶨側侾師偺僼傿儖僞偱偼側偔丄俠偲俼偑堦慻偩偗摥偔乮廃攇悢摿惈偺愜傟嬋偑傝偑堦売強偟偐柍偄乯扨弮側侾師偺僼傿儖僞偱偡丅
偱偡偐傜丄偙偺俀偮偺僼傿儖僞傪棟夝偱偒傟偽丄偦傟傪愙懕偟偰杦偳偺僼傿儖僞傪嶌傞偙偲偑偱偒傑偡丅
俀偮偺僼傿儖僞偺僀儊乕僕偼壓恾偺捠傝偱偡丅
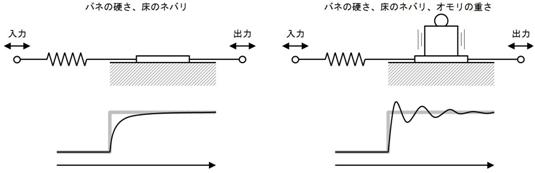
侾師偺僼傿儖僞偼忋恾嵍偺傛偆偵丄僰儖僰儖偡傞彴偲僶僱偺僀儊乕僕偱偡丅擖椡傪摦偐偡偲弌椡偑抶傟偰晅偄偰偒傑偡丅俀師偺僼傿儖僞偼忋恾塃偺傛偆偵丄僰儖僰儖偡傞彴偲丄僶僱偲僆儌儕偺僀儊乕僕偱偡丅擖椡傪摦偐偡偲弌椡偼抶傟偰摦偒偮偮丄儐儔儐儔偲梙傟傑偡丅偮傑傝侾師偺僼傿儖僞偼乽梙傟傞乿乮嫟怳偡傞乯惈幙偼偁傝傑偣傫偑丄侾師偺僼傿儖僞偼乮彴偺僱僶儕偑娚偄偲乯梙傟偑帩懕偡傞乮嫟怳偡傞乯惈幙偑偁傝傑偡丅
侾俆. 僗僥乕僩僶儕傾僽儖僼傿儖僞乮仛乯
俤倶們倕倢偑柍偄偲偒偼丄乽僼傿儖僞偺惓懱傪栚偱尒傞乿偙偲偼帄擄偺嬈偱偟偨丅僼傿儖僞偺惈幙偼丄尵偭偰傒傟偽乽抧宍乿偺傛偆側傕偺偱丄偦傟傪撿杒偵愗偭偨抐柺偵丄廃攇悢摿惈偑尰傟傞偺偱偡丅偲偙傠偑丄愄偼偙偺乽抧宍乿傪棫懱揑偵尒傞偙偲偑偱偒偢乽偙偙偵嶳偑偁傞敜偩偐傜乧偙偺曈偑惙傝忋偑偭偰乧乿摍偲暯柺揑側抧恾傪尒偰抧宍傪摢偺拞偱憐憸偟偰偄偨栿偱偡丅
偲偙傠偑崱擔偱偼丄壓恾偺傛偆偵僼傿儖僞偵懳墳偡傞抧宍傪俤倶倕們倕倢傪巊偭偰棫懱揑偵尒傞偙偲偑偱偒傑偡丅偱偡偐傜丄偦傟傪撿杒偵愗傟偽丄偳偺傛偆側廃攇悢摿惈偵側傞偺偐丄娙扨偵棟夝偡傞偙偲偑偱偒傑偡丅
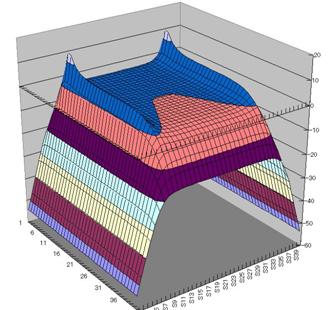
忋恾偼俀師僼傿儖僞偺廃攇悢揱払娭悢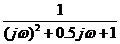 傪棫懱抧恾偵昤偄偨傕偺偱偡丅偙偺僌儔僼偼丄揱払娭悢傪=20*LOG(IMABS(IMDIV(1,IMSUM(IMPRODUCT(1,IMPOWER(Sheet1!B2,2)),IMPRODUCT(0.5,Sheet1!B2),1))),10)偲丄俤倶們倕倢偵擖椡偟偰丄摍崅慄僌儔僼傪巜掕偡傟偽昞帵偝傟傑偡丅乮嬶懱揑側庤弴偼屻偱愢柧偟傑偡乯
傪棫懱抧恾偵昤偄偨傕偺偱偡丅偙偺僌儔僼偼丄揱払娭悢傪=20*LOG(IMABS(IMDIV(1,IMSUM(IMPRODUCT(1,IMPOWER(Sheet1!B2,2)),IMPRODUCT(0.5,Sheet1!B2),1))),10)偲丄俤倶們倕倢偵擖椡偟偰丄摍崅慄僌儔僼傪巜掕偡傟偽昞帵偝傟傑偡丅乮嬶懱揑側庤弴偼屻偱愢柧偟傑偡乯
偝偰丄偙偺抧宍偑帵偡廃攇悢摿惈偼丄拞墰偱撿杒偵愗傟偽丄壓恾偵敀慄偱帵偡傛偆偵抐柺偵尰傟傑偡丅
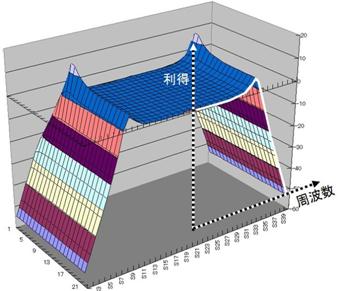
偮傑傝丄僼傿儖僞偺愝寁偲偼丄抧宍忋偱嶳偺埵抲傪條乆偵曄壔偝偣偰丄帺暘偺婓朷偡傞廃攇悢摿惈傪幚尰偡傞偙偲偱偡丅偙偺乽嶳乿偺偙偲傪乽億乕儖乿偲屇傫偱偄傑偡丅
幚嵺偵偼幚梡惈偺崅偄廃攇悢摿惈枅偵丄嵟揔側嶳偺攝抲偑婛偵暘偭偰偄傞偺偱丄偦偺攝抲偵側傞傛偆偵俠傗俼偺抣傪寛傔傞偙偲偱僼傿儖僞偑愝寁偱偒傑偡丅
侾. 崅廃攇
俀. 倓俛倣偲倓俛兪
僨僔儀儖偼嬌傔偰彫偝偄斾棪偐傜丄嬌傔偰戝偒偄斾棪傑偱丄庤抁偵彂偔偙偲偑偱偒偰旕忢偵曋棙偱偡丅偁傑傝偵曋棙側偺偱乽斾棪偟偐昞偝側偄偺偼栜懱柍偄乿乽倂偲摨條偵揹椡偺戝偒偝傕昞偟偨偄乿偲偄偆擬楏側僼傽儞偑尰傟傑偡丅
偦偙偱偲傝傢偗崅廃攇偺悽奅偱偼丄壓昞偵帵偡丄揹椡侾攞乮侽倓俛乯傪侾倣倂偲寛傔偨倓俛倣乮僨僔儀儖儈儕乯偲丄侾兪倂偲寛傔偨倓俛兪偑巊傢傟傑偡丅
|
倓俛倣乮僨僔儀儖儈儕乯
|
倓俛兪乮僨僔儀儖儅僀僋儘乯
|
|
婎弨偺揹椡
|
昞偡揹椡
|
倓俛倣偺抣
|
婎弨偺揹椡
|
昞偡揹椡
|
倓俛兪偺抣
|
|
侾倣倂
|
侽丏侽侽侾倣倂
|
亅俁侽倓俛倣
|
侾兪倂
|
侾兪倂
|
侽倓俛兪
|
|
侽丏侽侾倣倂
|
亅俀侽倓俛倣
|
侾侽兪倂
|
侾侽倓俛兪
|
|
侽丏侾倣倂
|
亅侾侽倓俛倣
|
侾侽侽兪倂
|
俀侽倓俛兪
|
|
侾倣倂
|
侽倓俛倣
|
侾倣倂
|
俁侽倓俛兪
|
|
侾侽倣倂
|
侾侽倓俛倣
|
侾侽倣倂
|
係侽倓俛兪
|
|
侾侽侽倣倂
|
俀侽倓俛倣
|
侾侽侽倣倂
|
俆侽倓俛兪
|
倓俛倣偺抣偵俁侽傪壛偊傞偲倓俛兪偺抣偵側傝傑偡丅偦傫側帠側傜丄偳偪傜偐堦曽偁傟偽椙偄敜偱偡偑丄倣倂傪椙偔巊偆恖傕嫃傟偽丄兪倂傪椙偔巊偆恖傕嫃傞偺偱丄椉曽偑懚嵼偟偰偄傑偡丅
倓俛倣傗倓俛兪偺抣偼師偺傛偆偵寁嶼偱偒傑偡丅
倓俛倣偺抣亖侾侽亊倢倧倗侾侽乮揹椡倂亐侾倣倂乯[倓俛倣]
僄僋僙儖偱偼丄倓俛倣偺抣=10*LOG(揹椡倂/1E-3,10)
倓俛兪偺抣亖侾侽亊倢倧倗侾侽乮揹椡倂亐侾兪倂乯[倓俛兪]
僄僋僙儖偱偼丄倓俛兪偺抣=10*LOG(揹椡倂/1E-6,10)
媡偵倓俛倣傗倓俛兪偐傜揹椡傪媮傔傞応崌偼丄
揹椡倂亖侾倣倂亊侾侽倓俛倣偺抣亐侾侽[倂]
僄僋僙儖偱偼丄揹椡倂=1E-3*10^( dBm偺抣/10)
揹椡倂亖侾兪倂亊侾侽倓俛兪偺抣亐侾侽[倂]
僄僋僙儖偱偼丄揹椡倂=1E-6*10^( dB兪偺抣/10)
俀.侾. 楙廗
條乆側揹椡傪丄倣倂丄兪倂丄倓俛倣丄倓俛兪偱帵偟偨壓昞偺嬻棑傪杽傔偰姰惉偟偰偔偩偝偄丅
|
僨僔儀儖
|
揹椡
|
僸儞僩
|
|
俀俁倓俛兪
|
俀侽侽兪倂
|
俀侽亄俁倓俛佁侾侽侽亊俀攞
|
|
丂丂丂丂丂丂倓俛兪
|
俆侽侽侽兪倂
|
俁侽亄俈倓俛佁侾侽侽侽亊俆攞
|
|
丂丂丂丂丂丂倓俛倣
|
俀侽侽侽倣倂
|
俁侽亄俁倓俛佁侾侽侽侽亊俀攞
|
|
侾俇倓俛兪
|
丂丂丂丂丂丂兪倂
|
|
|
係俇倓俛倣
|
丂丂丂丂丂丂倣倂
|
|
摎
|
僨僔儀儖
|
揹椡
|
峫偊曽
|
|
俀俁倓俛兪
|
俀侽侽兪倂
|
俀侽亄俁倓俛佁侾侽侽亊俀攞
|
|
丂丂丂丂俁俈倓俛兪
|
俆侽侽侽兪倂
|
俁侽亄俈倓俛佁侾侽侽侽亊俆攞
|
|
丂丂丂丂俁俁倓俛倣
|
俀侽侽侽倣倂
|
俁侽亄俁倓俛佁侾侽侽侽亊俀攞
|
|
侾俇倓俛兪
|
丂丂丂丂係侽兪倂
|
侾侽亄俇倓俛佁侾侽亊係攞
|
|
係俇倓俛倣
|
丂係侽侽侽侽倣倂
|
係侽亄俇倓俛佁侾侽侽侽侽亊係攞
|
俁. 倓俛倣倁偲倓俛兪倁
杮棃揹椡傪昞偡倓俛偱偡偑丄恖婥偼偝傜偵崅傑傝乽倓俛偱揹埑傕昞偟偨偄乿偲偄偆擬嫸揑側僼傽儞偝偊尰傟傑偡丅偦偙偱丄偲傝傢偗崅廃攇偺悽奅偱偼丄侾倣倁傪婎弨偵偟偨倓俛倣倁丄侾兪倁傪婎弨偵偟偨倓俛兪倁偑巊傢傟傑偡丅
偨偩偟丄壓昞偺傛偆偵丄揹埑偑侾侽攞偵側傞偲丄揹椡偑侾侽侽攞偵側傞偺偱丄侾侽攞偱俀侽倓俛戝偒偔側傞揰偵拲堄偑昁梫偱偡丅
|
倓俛倣倁乮僨僔儀儖儈儕儃儖僩乯
|
倓俛兪倁乮僨僔儀儖儅僀僋儘儃儖僩乯
|
|
婎弨偺揹椡
|
昞偡揹椡
|
倓俛倣倁偺抣
|
婎弨偺揹椡
|
昞偡揹椡
|
倓俛兪偺抣
|
|
侾倣倁
|
侽丏侽侽侾倣倁
|
亅俇侽倓俛倣倁
|
侾兪倁
|
侾兪倁
|
侽倓俛兪倁
|
|
侽丏侽侾倣倁
|
亅係侽倓俛倣倁
|
侾侽兪倁
|
俀侽倓俛兪倁
|
|
侽丏侾倣倁
|
亅俀侽倓俛倣倁
|
侾侽侽兪倁
|
係侽倓俛兪倁
|
|
侾倣倁
|
侽倓俛倣倁
|
侾倣倁
|
俇侽倓俛兪倁
|
|
侾侽倣倁
|
俀侽倓俛倣倁
|
侾侽倣倁
|
俉侽倓俛兪倁
|
|
侾侽侽倣倁
|
係侽倓俛倣倁
|
侾侽侽倣倁
|
侾侽侽倓俛兪倁
|
倓俛倣倁偺抣偵俇侽傪壛偊傞偲丄倓俛兪倁偺抣偵側傝傑偡丅倓俛倣倁傗倓俛兪倁偺抣偼師偺傛偆偵寁嶼偱偒傑偡丅
倓俛倣倁偺抣亖俀侽亊倢倧倗侾侽乮揹埑亐侾倣倁乯[倓俛倣倁]
僄僋僙儖偱偼丄揹埑dBmV=20*LOG(揹埑/1E-3,10)
倓俛兪俛偺抣亖俀侽亊倢倧倗侾侽乮揹埑亐侾兪俛乯[倓俛兪倁]
僄僋僙儖偱偼丄揹埑dB兪V =20*LOG(揹埑/1E-6,10)
媡偵倓俛倣倁傗倓俛兪倁偐傜揹椡傪媮傔傞応崌偼丄
揹埑[倁]亖侾倣倁亊侾侽倓俛倣倁偺抣亐俀侽
僄僋僙儖偱偼丄揹埑[倁]=1E-3*10^( dBmV偺抣/20)
揹埑[倁]亖侾兪倁亊侾侽倓俛兪倁偺抣亐俀侽
僄僋僙儖偱偼丄揹埑[倁]=1E-6*10^( dB兪V偺抣/20)
俁.侾. 楙廗
條乆側揹椡傪丄倣倁丄兪倁丄倓俛倣倁丄倓俛兪倁偱帵偟偨壓昞偺嬻棑傪杽傔偰姰惉偟偰偔偩偝偄丅
|
僨僔儀儖
|
揹埑
|
僸儞僩
|
|
俀俇倓俛兪倁
|
俀侽侽兪倁
|
俀俇亐俀亖侾俁
侾侽亄俁倓俛佁侾侽亊俀攞
|
|
丂丂丂丂丂倓俛倣倁
|
俀侽侽倣倁
|
俀侽亄俁倓俛佁侾侽侽亊俀攞
|
|
俇倓俛兪倁
|
丂丂丂丂丂兪倁
|
俇亐俀亖俁
|
|
丂丂丂俇俇倓俛倣倁
|
丂丂丂丂丂倣倁
|
|
|
丂丂丂丂丂倓俛兪倁
|
丂丂丂俀侽倣倁
|
|
俁.俀. 摎
俤倶們倕倢偱寁嶼偡傞応崌偼丄倓俛倣傗倓俛兪乮揹椡乯偲娫堘傢側偄傛偆偵丄倓俛倣倁傗倓俛兪倁乮揹埑乯偺寁嶼幃傪擖椡偟傑偡丅
埫嶼偱奣嶼偡傞応崌偼丄倓俛倣倁偲倓倁兪倁偼丄揹埑傪帵偡扨埵偱偡偐傜丄捠忢偺倓俛側傜侾侽侽侽攞偑俁侽倓俛倣偱偡偑丄揹埑偺応崌偼丄侾侽侽侽攞偱俇侽倓俛倣倁乮俀攞乯偲側傞揰偵拲堄偑昁梫偱偡丅偙偺偨傔丄揹埑偺倓俛偼乽媮傔偰偐傜俀攞偡傞乿偁傞偄偼乽傑偢俀偱妱偭偰偐傜張棟偡傞乿偲峫偊傞偲椙偄偱偡丅
偮傑傝丄椺偊偽係俇倓俛倣倁傪奣嶼偱揹埑偵栠偡偲偒偼丄嵟弶偵俀偱妱偭偰俀俁倓俛偲峫偊丄俀侽亄俁倓俛佁侾侽侽亊俀攞偲峫偊偰丄俀侽侽倣倁偲媮傔傑偡丅媡偵丄揹埑偺俀侽侽攞傪乮壖偵揹椡偺俀侽侽攞棪偲峫偊偰乯俀俁倓俛偵捈偟偨屻偱丄俀攞偡傞偙偲偱丄係俇倓俛偲摎偊傑偡丅
|
僨僔儀儖
|
揹埑
|
峫偊曽
|
|
俀俇倓俛兪倁
|
俀侽兪倁
|
俀俇亐俀亖侾俁
侾侽亄俁倓俛佁侾侽亊俀攞
|
|
丂丂丂係俇倓俛倣倁
|
俀侽侽倣倁
|
俀侽亄俁倓俛佁侾侽侽亊俀攞
俀俁亊俀亖係俇
|
|
俇倓俛兪倁
|
丂丂丂丂俀兪倁
|
俇亐俀亖俁
俁倓俛佁俀攞
|
|
俇俇倓俛倣倁
|
丂俀侽侽侽倣倁
|
俇俇亐俀亖俁俁
俁侽亄俁倓俛佁侾侽侽侽亊俀攞
|
|
丂丂丂俉俇倓俛兪倁
|
俀侽倣倁
|
係侽亄俁倓俛佁侾侽侽侽侽亊俀攞
係俁亊俀亖俉俇
|
係. 捈棳傗掅廃攇偲丄崅廃攇偺堘偄乮仛乯
乮梺憛偺搾偲攇棫偮悈憛偱愢柧乯
俆. 斀幩偲俽僷儔儊乕僞乕乮仛乯
俇. 惓婯壔僀儞僺乕僟儞僗乮仛乯
俈. 僀儞儈僞儞僗乮僗儈僗乯僠儍乕僩乮仛乯
奐儖乕僾惂屼偲暵儖乕僾惂屼
俹俬俢惂屼
俤倶們倕倢偲惂屼
尰戙惂屼
旝暘愭峴宆惂屼
僼傿乕僪僼僅傾乕僪惂屼
斾椺抣僼傿乕僪僼僅傾乕僪惂屼
斾椺抣僼傿乕僪僼僅傾乕僪惂屼
奜棎僆僽僓乕僶乕惂屼
僷僗僐儞
僌儔僂儞僪
僔乕儖僪
怣崋慄
儐僯僶乕僒儖婎斅幚憰偺僥僋僯僢僋
侾. 杮彂偵彂偄偨帠丄彂偐側偐偭偨帠
帺暘偱敀巻偐傜峫偊側偔偰傕丄僨乕僞僔乕僩摍偵徯夘偝傟偨條乆側墳梡夞楬傪慻傒崌傢偣傞偩偗偱傕丄寢峔妝偟偄岺嶌偑偱偒傞傕偺偱偡丅偲偙傠偑丄偦傟偧傟偺墳梡夞楬偑偳偆偄偆嬝摴偱摦嶌偟偰偄傞偐偲偄偆愢柧偑彮側偄偺偱丄徯夘偝傟偨夞楬傪傾儗儞僕偡傞偲側傟偽丄媫偵僴乕僪儖偑忋偑傝傑偡丅
傕偪傠傫丄岺妛彂傪堷偭挘傝弌偟偰撉傒夝偔偙偲偱丄偄偮偐偼偦傟傜偺夞楬偺摦嶌傪棟夝偡傞偙偲偑偱偒傞偱偟傚偆丅偱傕丄妝偟偄揹巕岺嶌偺偨傔偵丄偮傑傜側偄岺妛彂傪撉傓偲偄偆偺偼丄壗偐堘偆傛偆偵巚偊傑偡丅
墳梡偺棙偔丄偪傚偭偲偼崻尮惈偺偁傞棟孅傪丄懡彮偺岆夝傪妎屽偟偨忋偱暘傝堈偔愢柧偡傞偺偼乮偦傟傎偳崲擄偱偼柍偄偲偟偰傕乯旕忢偵柺搢偱丄乮傑偲傕側杮偵偟偰弌偣傞傛偆側榖偱傕側偄偺偱乯尒曉傝偺柍偄暘栰偱偡丅杮彂偱偼偦偺乽柺搢偱尒曉傝偺柍偄晹暘乿偵徟揰傪偁偰偰暔岲偒側夝愢傪揥奐偟傑偟偨丅
偱偡偐傜丄岼偵懡偔徯夘偝傟偰偄傞婎杮揑側墳梡夞楬摍偼偁偊偰妱垽偟偰偄傑偡丅晹昳儊乕僇乕偺僒僀僩傪扵偣偽丄傾僾儕働乕僔儑儞僲乕僩摍偲偟偰柺敀偄墳梡夞楬偑戲嶳徯夘偝傟偰偄傑偡偐傜丄偤傂嶲徠偟偰偔偩偝偄丅
![]() 偲寁嶼偟偰媮傔傑偡偑丄傑偢悢帤偩偗偵拲栚偟偰丄
偲寁嶼偟偰媮傔傑偡偑丄傑偢悢帤偩偗偵拲栚偟偰丄![]() 偲寁嶼偟丄師偵扨埵偩偗傪
偲寁嶼偟丄師偵扨埵偩偗傪![]() 偲寁嶼偟偰丄椉幰傪崌傢偣偰5M兌偲摎傪弌偟傑偡丅
偲寁嶼偟偰丄椉幰傪崌傢偣偰5M兌偲摎傪弌偟傑偡丅![]() 摍偺乽扨埵偺寁嶼乿偼帺慠偲妎偊傑偡偑丄姷傟傞傑偱偼丄忔悢偱寁嶼偟傑偡丅崱夞偺椺偱偼壓恾偺傛偆偵丄
摍偺乽扨埵偺寁嶼乿偼帺慠偲妎偊傑偡偑丄姷傟傞傑偱偼丄忔悢偱寁嶼偟傑偡丅崱夞偺椺偱偼壓恾偺傛偆偵丄![]() 傪
傪![]() 偲峫偊丄暘曣偺(-3)偺晞崋偼斀揮偟偰(+3)偐傜崌嶼偟偰丄(6)=M偲峫偊傑偡丅
偲峫偊丄暘曣偺(-3)偺晞崋偼斀揮偟偰(+3)偐傜崌嶼偟偰丄(6)=M偲峫偊傑偡丅



![]() 偱丄揹埑偼怟旜偵朹偺偮偄偨栴報
偱丄揹埑偼怟旜偵朹偺偮偄偨栴報 ![]() 偱帵偟傑偡丅
偱帵偟傑偡丅![]() 偱帵偡曽朄傕偁傝傑偡偑丄偙偺曽朄偱偼揹埑偺曽岦偑暘傜側偄偺偱丄杮彂偱偼巊偄傑偣傫丅
偱帵偡曽朄傕偁傝傑偡偑丄偙偺曽朄偱偼揹埑偺曽岦偑暘傜側偄偺偱丄杮彂偱偼巊偄傑偣傫丅
![]() 偱丄岎棳傪揰慄
偱丄岎棳傪揰慄 ![]() 偱帵偟傑偡丅
偱帵偟傑偡丅

![]()








![]() 偲俽偺乯俀偮偁傝傑偡丅兌乮俷俫俵乯偺媡悢偑
偲俽偺乯俀偮偁傝傑偡丅兌乮俷俫俵乯偺媡悢偑 ![]() 乮俵俫俷乯偲偄偆偺偼丄偍拑栚偱妎偊堈偄偨傔丄惀旕巊偄偨偄偺偱偡偑丄
乮俵俫俷乯偲偄偆偺偼丄偍拑栚偱妎偊堈偄偨傔丄惀旕巊偄偨偄偺偱偡偑丄![]() 偲偄偆暥帤偑柍偄偨傔丄杮彂偱偼俽乮僕乕儊儞僗乯傪巊偄傑偡丅
偲偄偆暥帤偑柍偄偨傔丄杮彂偱偼俽乮僕乕儊儞僗乯傪巊偄傑偡丅




![]()



![]()
![]()






![]() 仼偙偺幃偼暘傜側偔偰傕椙偄
仼偙偺幃偼暘傜側偔偰傕椙偄![]() 仼偙偺幃偼暘傜側偔偰傕椙偄
仼偙偺幃偼暘傜側偔偰傕椙偄



![]()



![]()



























 丂丂丂
丂丂丂









![]() 丂偮傑傝丄
丂偮傑傝丄![]()


![]()