僶僀億乕儔僩儔僕僗僞夞楬偺愝寁
偼偠傔偵
丂偙偺儁乕僕偱偼丄僶僀億乕儔僩儔儞僕僗僞傪巊梡偟偨夞楬傪愝寁偡傞偨傔偺抦幆偺堦晹傪採嫙偟傑偡丅偙偺儁乕僕傪嶌傞偵偁偨偭偰棷堄偟偨揰偼師偺捠傝偱偡丅
- 幚梡揑側夞楬愝寁偑抁帪娫偱偱偒傞傛偆偵偡傞偙偲丄偦偺偨傔偵偼妛栤揑側尩枾偝傪媇惖偵偡傞偙偲
- 悢幃傪彮側偔偟偰乽恾乿偲乽僀儊乕僕乿偱棟夝偱偒傞傛偆愢柧偡傞偙偲
- 摍壙夞楬偵抲偒姺偊傞偙偲側偔丄夞楬恾傪尒偰捈愙揑偵摦嶌傪棟夝偟丄愝寁偱偒傞傛偆偵偡傞偙偲
- 岞幃傪妎偊偰昞柺揑偵愝寁偱偒傞偺偱偼側偔丄崻尮揑側棟夝傪尦偵愝寁偱偒傞傛偆偵偡傞偙偲
仺崻尮揑偵棟夝偟偰愝寁偄側偄偲丄夞楬偵栤戣偑婲偒偨偲偒丄尨場傪夝柧偟偰夝寛偱偒傑偣傫丅崲傝傑偡偹丅
- 僩儔儞僕僗僞夞楬愝寁偺棟夝偵昁梫側婎慴揑側撪梕傕愢柧偡傞偙偲
- 婎慴揑側撪梕傕丄昁梫偵側傞搒搙徯夘偟偰丄梊旛抦幆偑彮側偔偰傕棟夝偱偒傞傛偆偵偡傞偙偲
- 愢柧偼弴彉傪柧妋偵偟偰丄夝傝堈偔岺晇偡傞偙偲
丂扐偟丄撪梕揑偵偼屆偄偱偡丄偨偲偊偽丄揹椡夞楬偱傕僷儚乕俵俷俽俥俤俿偱偼側偔丄僶僀億乕儔偺僷儚乕僩儔儞僕僗僞傪巊梡偟偰愢柧偟偰偄傑偡丅偝傜偵丄掞峈偺恾婰崋偵偮偄偰傕丄侾俋俆俀擭偵惂掕偝傟偨俰俬俽丂俠丂侽俁侽侾偺媽婰崋乮僊僓僊僓偺儅乕僋乯傪抪傜偆帠側偔巊偭偰偄傑偡丅偙傟偼丄尰応偺媄弍幰偑尰帪揰偱偼掞峈傪媽俰俬俽婰崋偱彂偄偰偄傞尰幚偑偁傞偐傜偱偡丅
丂偟偐偟丄僶僀億乕儔僩儔儞僕僗僞傪巊偭偨夞楬愝寁偑暘偐偭偰偟傑偊偽丄偁偲偼丄怴偟偄慺巕偵偮偄偰偺曌嫮傪曗偆偙偲偱丄偦傟傜偺慺巕傪巊偭偨夞楬傪愝寁偡傞偙偲偼梕堈偱偡丅
丂婎杮揑側峫偊曽偼丄柤挊亀僾儘僌儔儉妛廗偵傛傞敿摫懱夞楬嘥亁亀僾儘僌儔儉妛廗偵傛傞敿摫懱夞楬嘦亁乮怑嬈擻椡奐敪嫵嵽埾堳夛曇廤乯偵弨嫆偟偰偍傝丄偦傟傪曗姰偟丄敪揥偝偣偨撪梕偵側偭偰偄傑偡丅偱偡偐傜丄岎棳怣崋偵偮偄偰偼丄僄儈僢僞摍壙僀儞僺乕僟儞僗re偱峫偊傑偡丅傑偨丄偙偺偨傔忋婰彂愋偲撪梕偑椶帡偡傞晹暘偑尰傟傑偡偑丄偙傟偼丄僩儔儞僕僗僞傪愢柧偡傞偨傔偵偼巇曽偺側偄帠偱偡偺偱偍嫋偟偔偩偝偄丅
丂亀敿摫懱夞楬嘥嘦亁偼柤挊偱偡偑丄儁乕僕悢偺惂尷忋偐丄廳梫側偄偔偮偐偺揰偺愢柧偑寚棊偟偰偍傝丄巆擮側偑偦偺晹暘傪曗傢側偗傟偽丄幚梡揑側夞楬傪愝寁偡傞偙偲偑偱偒傑偣傫丅偙偺儁乕僕偱偼偦偺揰偵傕尵媦偟偰乽愝寁偱偒傞両乿乽嶌傟傞両乿乽摦嶌偡傞両乿乽巊偊傞両乿傪栚巜偟偰彂偒恑傔傑偡丅
幚嵺偺愙懕偲丄夞楬恾偺昞婰
丂偄偒側傝夞楬恾偑弌偰偒傑偟偨偑丄恾偺夞楬偑偳偺傛偆側摦嶌傪偡傞偺偐丄崱偼慡偔棟夝偡傞昁梫偼偁傝傑偣傫丅偙偙偱偼丄夞楬恾偺彂偒曽傪愢柧偟傑偡丅
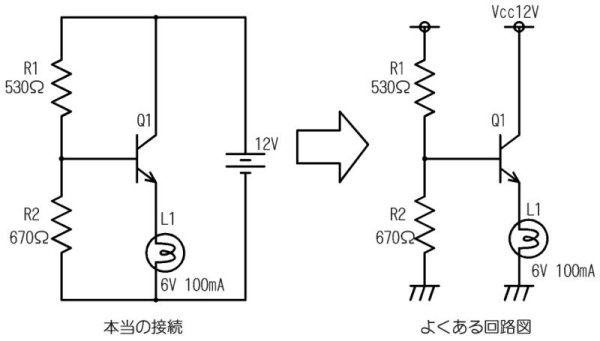
幚嵺偺愙懕偲夞楬恾偺昞婰
丂夞楬恾偼昤偔庤娫傪徣偔偨傔丄幚嵺偵攝慄偡傞捠傝偵偼彂偒傑偣傫丅恾偺嵍懁偑杮摉偺愙懕乮攝慄乯丄塃懁偑夞楬恾偺椺偱偡丅
億僀儞僩偼乧
- 揹尮乮侾俀倁偺揹抮乯偼徣棯偝傟傑偡
- 揹尮乮侾俀倁偺晹暘乯偺攝慄偼婰崋偱昞偝傟傑偡
- 侽倁偺晹暘偼傾乕僗婰崋偱昞偝傟傑偡
- 揹慄偑岎傢傝丄愙懕偟偰偄傞晹暘偵偼昁偢乽崟娵乿傪晅偗傑偡
- 乮摦嶌傪棟夝偟堈偔偟偨偄側傜乯揹埑偺崅偄晹暘傪恾偺忋懁偵丄揹埑偺掅偄晹暘傪壓懁偵彂偒傑偡
偙偺傛偆偵彂偔偙偲偱夞楬傪娙慺偵彂偒昞偡偙偲偑偱偒丄姷傟傟偽暘偐傝傗偡偔側傝傑偡丅
捈棳揹埑偲揹棳偺恾帵
丂偙偺儁乕僕偱偼夞楬偺摦嶌傪僀儊乕僕偱懆偊傜傟傞傛偆偵丄揹埑偲揹棳傪撈摿偺婰崋偱昞偟傑偡丅偙傟偼俰俬俽側偳偺婯奿偱寛傔傜傟偨傕偺偱偼側偔丄棟夝偟堈偄傛偆偵偙偺儁乕僕偑撈帺偵嵦梡偟偰偄傞傕偺偱偡丅
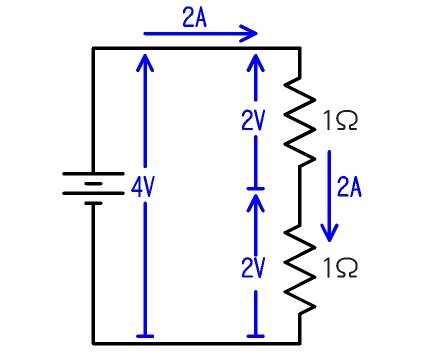
捈棳揹埑偲揹棳偺恾帵
億僀儞僩偼
- 揹埑偲揹棳傪栴報偱昞偟傑偡
- 揹埑偲揹棳傪偺婰崋傪嬫暿偡傞偨傔偵丄揹埑偺栴報偼偍怟偵墶朹傪晅偗傑偡
揹埑傪椉曽偵栴偠傝偺偮偄偨婰崋偱昞婰偡傞曽朄偑偁傝傑偡偑丄偙傟偱偼揹埑偺曽岦偑暘偐傜側偄偐傜偱偡丅
僆乕儉偺朄懃偼弖娫偱巊偊傞傛偆偵側傠偆乮媽幃乯
丂偩傟偱傕抦偭偰傞僆乕儉偺朄懃丄偱傕丄夞楬傪尒側偑傜帺桼帺嵼偵巊偆偵偼乽弖娫偱巊偊傞乿偲偄偆偙偲偑戝愗偱偡丅愄偐傜偁傞曽朄偼丄師偺傛偆偵側傕偺偱偡偑丄偁傑傝偍姪傔偟傑偣傫丅
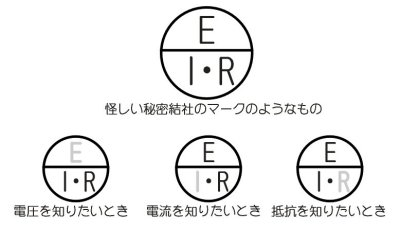
僆乕儉偺朄懃偺巊偄曽乮媽幃乯
丂恾偺忋拞墰偵昤偄偨丄夦偟偄旈枾寢幮偺儅乕僋偺傛偆側傕偺傪彂偄偰丄帺暘偺媮傔偨偄抣傪巜偱塀偟傑偡丄偨偲偊偽丄揹棳俬傪媮傔偨偄偲偡傟偽丄I偺晹暘傪塀偣偽俤亐俼偱媮傔傜傟傞偙偲偑暘偐傞偲偄偆傕偺偱偡丅
僆乕儉偺朄懃偼弖娫偱巊偊傞傛偆偵側傠偆乮怴宆乯
丂偟偐偟丄忋偱愢柧偟偨曽朄偵偼擄揰傕偁傝傑偡丅偄偪偄偪旈枾寢幮偺儅乕僋傪彂偐側偔偰偼側傝傑偣傫丅儅乕僋傪朰傟傞偙偲傕偁傝傑偡丅懡偔偺恖偵帋偟偨偲偙傠丄偙偺曽朄傛傝丄師偺曽朄偑桪傟偰偄傑偟偨丅
偍姪傔偺乽僆乕儉偺朄懃傪弖娫偱巊偆曽朄乿偼
- 揹埑偼昁偢妱傜傟傞乮塣柦偵偁傞乯
- 揹埑偑弌偰棃側偗傟偽丄俀偮傪妡偗傞
偙偺俀偮偩偗傪妎偊傑偡丅
亂椺侾亃
乽俀俙棳偟偨傜丄俇倁敪惗偟偨掞峈偑偁傝傑偡丅壗兌偱偡偐乿
仺乽揹埑偺俇倁偼昁偢妱傜傟傞乿塣柦偵偁傝傑偡偺偱丄摎偊偼丄
仺丂俇倁亐俀俙亖俁兌
偲媮傔傑偡丅
亂椺俀亃
乽俇兌偺掞峈偵俀俙棳偟偨傜丄壗倁偺揹埑偑敪惗偟傑偡偐乿
仺乽揹埑偺抣偑弌偰棃側偄偺偱丄弌偰偒偨抣俀偮傪妡偗偰乿
仺俇兌亊俀俙亖侾俀倁
偲媮傔傑偡丅
姷傟傞偲丄偙偺曽朄偑憗偄偱偡丅
僩儔儞僕僗僞偺乽偁傝偑偨偝乿偲俁偮偺億僀儞僩
丂僩儔儞僕僗僞偺巊偭偨夞楬傪愝寁偡傞偨傔偵偳偆偟偰傕
昁梫側抦幆偼偦傟傎偳懡偔偁傝傑偣傫丅椺偊偽丄捈棳偱
偺摦嶌偵偮偄偰偼丄師偺恾偵帵偡乽俁偮偺億僀儞僩乿偝偊
抦偭偰偄傟偽丄夞楬偺忬懺傪棟夝偱偒傑偡丅
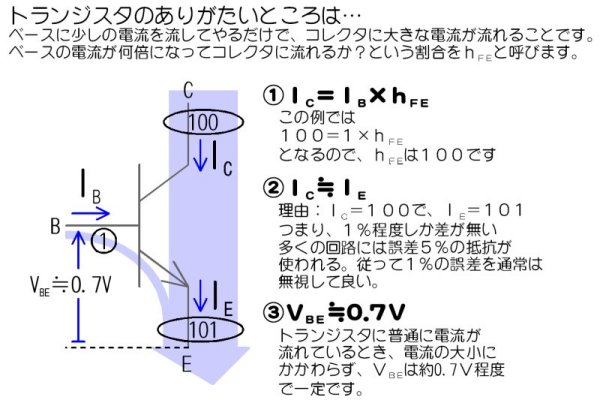
僩儔儞僕僗僞偺俁偮偺億僀儞僩
偮傑傝僩儔儞僕僗僞偺俁偮偺億僀儞僩偲偼
- 俬俠亖俬俛亊倛俥俤
丂俬俛偺倛俥俤攞偺俬俠偑棳傟傞
丂俬俛偼俬俠偺倛俥俤暘偺侾偱偁傞丅
- 俬俠佮俬俤
丂俬俠偲俬俤偼摨偠偲峫偊傞
- 倁俛俤佮侽丏俈倁
丂僄儈僢僞偲儀乕僗偺娫偺揹埑倁俛俤偼僩儔儞僕僗僞偑晛捠偵揹棳傪棳偟偰偄傟偽丄棳偡揹棳偺戝偒偝偵偐偐傢傜偢丄奣偹侽丏俈倁偱偁傞
俁偮偺億僀儞僩偱壗偑弌棃傞
丂偝偰丄偨偭偨俁偮偺億僀儞僩偩偗偱壗偑弌棃傞偺偐丄偙傟偐傜
帋偟偰傒傑偟傚偆丅
栤戣
丂偺夞楬傪尒偰偔偩偝偄丅僐儗僋僞偵偼俇倠兌丄僄儈僢僞
偵偼侾倠兌偑愙懕偝傟偰偄傑偡丅揹尮揹埑偑侾俀倁偱丄儀乕僗偵侾丏俈倁傪壛偊偰偄傑偡丅
- 弌椡揹埑倁俷偼壗倁偵側傞偱偟傚偆偐
- 儀乕僗偵棳傟崬傓揹棳俬俛偼偄偔傜偵側傞偱偟傚偆偐
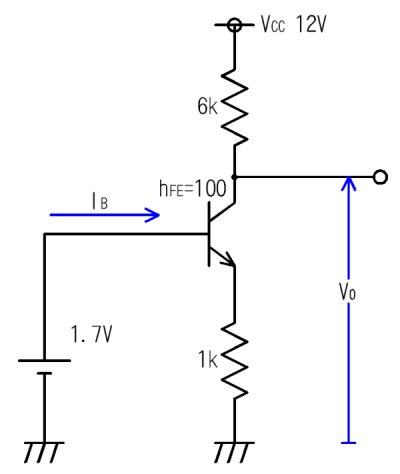
俁偮偺億僀儞僩偱壗偑偱偒傞偐
摎偊
丂偙偺栤戣偵丄僩儔儞僕僗僞偺俁偮偺億僀儞僩偲丄僆乕儉偺朄懃偩偗偱摎偊偰備偒傑偡丅壓偺恾偺嘆嘇嘊乧偺斣崋偲丄師偺愢柧偺斣崋偑懳墳偟偰偄傑偡丅
- 儀乕僗偵偼侾丏俈倁偑壛傢偭偰偄傞
- 僩儔儞僕僗僞偺倁俛俤偼奣偹侽丏俈倁偱偁傞
- 廬偭偰丄僄儈僢僞掞峈俼俤偵壛傢傞揹埑偼侾倁偱偁傞
- 俼俤偼侾倠兌偱偁傞偐傜丄棳傟傞揹棳俬俼俤偡側傢偪丄俬俤偼侾倣俙偱偁傞
- 俬俠偼俬俤偲傎傏摍偟偄偺偱傗偼傝侾倣俙偱偁傞
- 俇倠兌偺俼俴偵侾倣俙偑棳傟偰偄傞偺偱丄偦偙偵偼丄俇倁偺揹埑偑敪惗偟偰偄傞
- 揹尮揹埑偑侾俀倁偱偁傞丅
- 揹尮揹埑偐傜倁俼俴乮俇倁乯偩偗壓偑偭偨揹埑偑倁俷偱偁傞丅偩偐傜丄倁俷偼俇倁偱偁傞丅
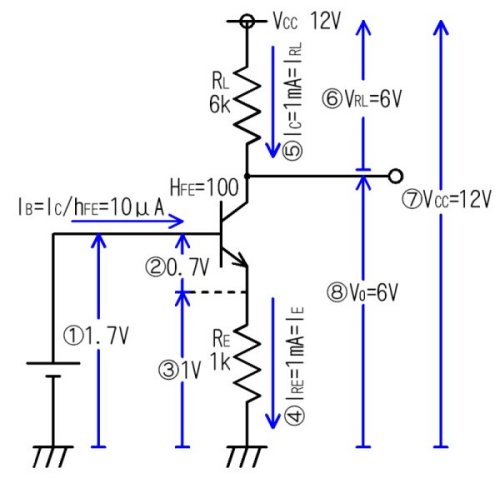
俁偮偺婎杮偱壗偑偱偒傞偐
丂偙偺傛偆偵丄俁偮偺億僀儞僩偩偗偱娙扨側夞楬偺摦偒傪棟夝偡傞偙偲偑偱偒傑偟偨丅偝傜偵夞楬偑暋嶨偵側偭偰傕丄偙偺俁偮偺億僀儞僩偼妶桇偟懕偗傑偡丅
偍丄憹暆偟偰傞両
丂愭掱偺夞楬偱偼儀乕僗偵侾丏俈倁偺揹埑傪壛偊偰偄傑偟偨丅偙傟傪丄嬐偐侽丏俁倁憹傗偟偰丄儀乕僗偵俀倁傪壛偊傞偲丄夞楬偺忬懺偼偳偺傛偆偵曄壔偡傞偱偟傚偆偐丅
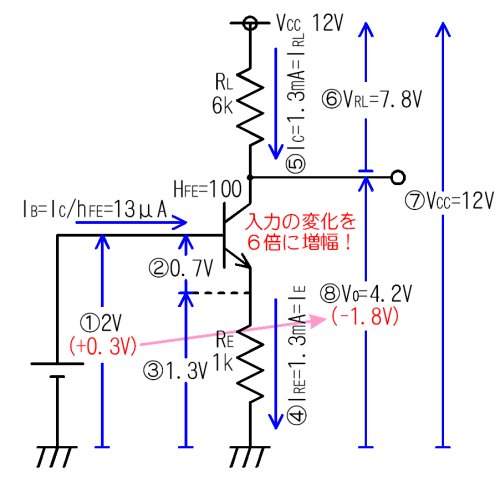
憹暆偟偰傞偧両
丂擖椡揹埑傪嬐偐侽丏俁倁憹傗偟偨偩偗側偺偵丄弌椡揹埑偼侾丏俉倁傕掅壓偟傑偟偨丅偮傑傝偙偺夞楬偼丄擖椡偺揹埑偺曄壔傪俇攞偵憹暆乮奼戝乯偡傞偙偲偑偱偒傞偺偱偡丅憹暆偺妱崌偼丄奣偹俼俴乛俼俤偱媮傑傝傑偡丅乮徻偟偔偼屻掱乯
丂偙傟偑僩儔儞僕僗僞偵傛傞揹埑憹暆偺婎杮偺尨棟偱偡丅
僩儔儞僕僗僞傪埨掕摦嶌偝偣傞乮僶僀傾僗乯
丂愭掱偺夞楬偱丄儀乕僗偵侾丏俈倁偺揹抮傪偮側偄偱偄偨傛偆偵丄僩儔儞僕僗僞偼丄儀乕僗偵堦掕偺揹埑傪壛偊傞偙偲偱丄弶傔偰摦嶌偟傑偡丅偙傟傪乽儀乕僗偵僶僀傾僗揹埑傪妡偗傞乿偲傕偄偄傑偡丅
丂愭掱偺椺偺傛偆偵揹抮傪巊偆偲丄偦偺偆偪柍偔側傝傑偡偟丄抣抜傕崅偄偺偱丄揹尮揹埑傪俀杮偺掞峈乮晛捠俼俙偲俼俛偲屇傇乯偱暘埑偟偰丄揹埑傪嶌傝傑偡丅壓偺夞楬恾偼栺俀攞偺揹埑憹暆婍偱偡丅岻傒偵寁嶼偟偰儀乕僗偵僶僀傾僗揹埑傪妡偗偨偮傕傝偱偡丅
丂儀乕僗揹埑偼俀丏俈倁偵僶僀傾僗偝傟丄僄儈僢僞偵偼侾倣俙偺僶僀傾僗揹棳偑棳傟偰偄傑偡丅
丂俼俙偵棳傟偨俀侽兪俙偺偆偪丄侾侽兪俙偼儀乕僗傊棳傟偰偟傑偆偺偱丄俼俛偵偼侾侽兪俙偟偐棳傟側偄偲峫偊偰愝寁偟偰偄傑偡丅俼俙偵棳偡揹棳偑俀侽兪俙偲彫偝偄偺偱徚旓揹棳傕彮側偔丄堦尒桪廏側愝寁偵尒偊傑偡偹丅
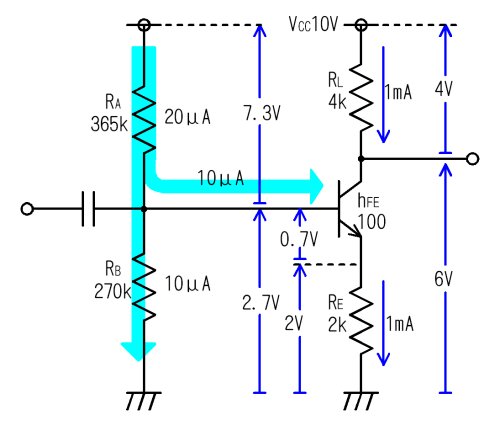
岻傒偵寁嶼偟偨乮偮傕傝乯偺僶僀傾僗夞楬
丂偲偙傠偑偳偭偙偄丅僩儔儞僕僗僞偺倛俥俤偵偼捠忢俀攞掱搙偺岆嵎偑偁傞偺偱偡丅椺偊偽丄摨偠昳庬偺摨偠儔儞僋偱傕丄倛俥俤亖侾侽侽乣俀侽侽偲偄偆姶偠偱斖埻偑峀偄偺偱偡丅忋偺夞楬恾偼傄偭偨傝侾侽侽偲偟偰寁嶼偟偰偄傑偡偑丄塣埆偔乮塣椙偔乯倛俥俤亖俀侽侽偺僩儔儞僕僗僞偑傗偭偰偒偨傜偳偆側傞偐丄壓偺恾偱尒偰傒傑偟傚偆丅
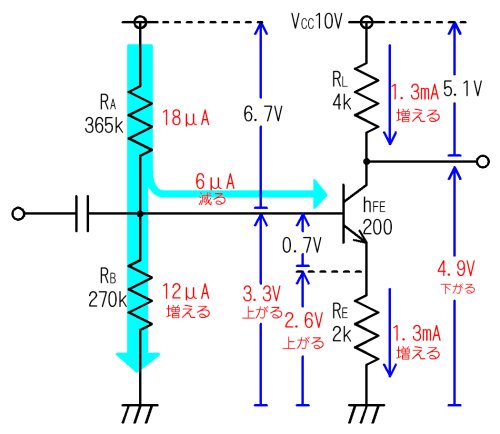
俫俥俤偑曄傢偭偨傜憤曵傟
丂倛俥俤偑俀侽侽偵戝偒偔側傞偲丄儀乕僗揹棳偼侾侽兪俙偐傜俇兪俙偵尭彮偟丄儀乕僗僶僀傾僗揹埑倁俛俛傕俀丏俈倁偐傜俁丏俁倁傊偲戝暆忋徃丅偦偺偆偊丄僄儈僢僞揹棳俬俤俤傕侾倣俙偐傜侾丏俁倣俙偵憹壛丄寢壥偲偟偰弌椡揹埑倁俷俷偼摉弶梊掕偺俇倁偐傜丄係丏俋倁偵尭彮偟偰偟傑偄傑偟偨丅杦偳憤曵傟忬懺偱偡丅巊偄暔偵側傝傑偣傫偹丅
丂偙偺傛偆側憤曵傟忬懺傪杊偖偨傔偵乽俼俙偲俼俛偵棳偡揹棳傪働僠働僠偟側偄乿偙偲偑戝愗偱偡丅彮側偔偲傕儀乕僗揹棳乮偙偺椺偱偼侾侽兪俙乯偺侾侽攞丄弌棃傟偽俀侽乣俁侽攞 偨偭傉傝偲棳偟傑偡丅俼俙傗俼俛偵弶傔偐傜僞僢僾儕揹棳偑棳傟偰偄傟偽丄儀乕僗傊棳傟傞揹棳偑懡彮曄壔偟傛偆偑丄俼俛偺揹棳偺曄壔偺妱崌偼彫偝偔側傝丄儀乕僗偺僶僀傾僗揹埑傕杦偳曄壔偟側偄丄偲峫偊傞偺偱偡丅侾侽侽墌偟偐帩偭偰側偄偲偒偵丄俆侽墌偺攦偄暔傪偡傞偲丄偍嬥偑敿暘偵尭偭偰偟傑偄傑偡偑丄侾侽侽侽侽墌帩偭偰偄傞側傜丄俆侽墌偔傜偄巊偭偰傕丄尭偭偨婥偑偟側偄乮堦枩墌嶥傪曵偡偺偼夨偟偄偑乧乯偺偲摨偠偱偡偹丅
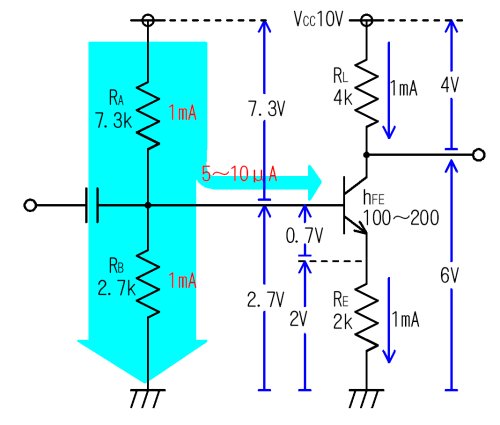
僞僢僾儕偲僶僀傾僗揹棳俬俼俙俛傪棳偟偨夞楬
丂忋偺夞楬偼偪傚偭偲傗傝偡偓偐傕偟傟傑偣傫偑乮侾侽侽攞傕棳偟偰傞乯俼俙傗俼俛偵侾倣俙傕棳偟偰偍偗偽丄儀乕僗揹棳偑侾侽兪俙偱偁傠偆偑丄俆兪俙偱偁傠偆偑丄儀乕僗僶僀傾僗揹埑偺俀丏俈倁偼價僋偲傕偟傑偣傫丅堦斒偵偼侾侽攞偐傜俀侽攞偁偨傝偑椙偔巊傢傟偰偄傞傛偆偱偡丅
僩儔儞僕僗僞偺俁偮偺忬懺乽岺帠拞乿
丂僩儔儞僕僗僞偵偼俷俶乛俷俥俥乛儕僯傾偺俁偮偺忬懺偑偁傞偲尵偆偙偲傪夞楬恾偲僌儔僼傪廳偹崌傢偣偰僀儊乕僕偱愢柧偟傑偡丅
僗僀僢僠儞僌夞楬
丂乽徠柧傪俷俶乛俷俥俥傪偡傞乿偲偄偆傛偆偵丄巹払偺恎偺夞傝偵偼丄俷俶偲俷俥俥偩偗偱偒傟偽丄偦傟偱廫暘栶偵棫偮応崌偑戲嶳偁傝傑偡丅偙偺傛偆側応崌偵丄僩儔儞僕僗僞偺俷俶忬懺偲俷俥俥忬懺傪棙梡偟偰丄僗僀僢僠儞僌偲偄偆摦嶌傪偝偣傑偡丅偮傑傝丄僩儔儞僕僗僞傪僗僀僢僠偲偟偰巊梡偡傞栿偱偡丅偦偺傛偆側夞楬傪乽僗僀僢僠儞僌夞楬乿偲屇傫偱偄傑偡丅偙偙偱偼丄娙扨側僗僀僢僠儞僌夞楬傪愝寁偡傞曽朄傪弴傪捛偭偰夝愢偟傑偡丅
儀乕僗偵棳偡揹棳偲乽僆乕僶乕僪儔僀僽乿
丂僩儔儞僕僗僞偺俷俶乛俷俥俥傪棙梡偟偰乽僗僀僢僠傪墴偡偲丄儔儞僾偑岝傞乿偲偄偆扨弮側夞楬傪峫偊偰傒傑偡丅
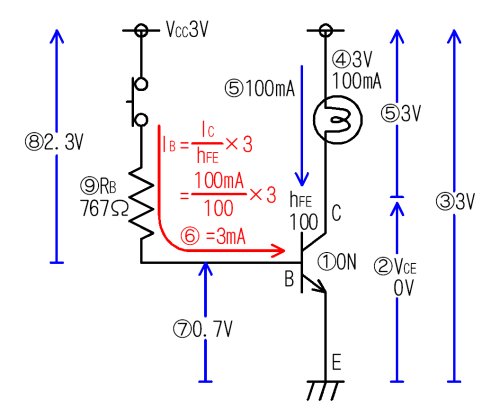
儀乕僗偵棳偡揹棳傪峫偊傞
忋偺夞楬恾偺嘆乣嘓偺斣崋偑丄師偺愢柧偺斣崋偲懳墳偟偰偄傑偡偐傜丄弴偵尒偰傒傑偟傚偆丅
- 摛媴傪岝傜偣傞偨傔偵偼僩儔儞僕僗僞傪俷俶偵偡傞
- 偡傞偲丄僩儔儞僕僗僞偺倁俠俤偼侽倁偲側傞丅
- 揹尮揹埑偼俁倁偩偐傜乧
- 摛媴偵偼俁倁偑壛傢傞乮傕偪傠傫摛媴偑揰摂偡傞乯
- 俁倁丄侾侽侽倣俙偺摛媴偩偐傜丄侾侽侽倣俙偺俬俠偑棳傟傞
- 偦偙偱丄俬俛偼俬俠乮侾侽侽倣俙乯偺倛俥俤乮侾侽侽乯暘偺侾丄偮傑傝侾倣俙棳偣偽傛偄敜偩丄偲偙傠偑丄偙偙偱偼偦偺捠傝偵偼峴偐側偄
側偤側傜丄僩儔儞僕僗僞偑俷俶偵側傞乮偮傑傝丄倁俠俤偑彫偝偔側傞乯偲倛俥俤偑俁暘偺侾偔傜偄偵尭彮偟偰偟傑偆偐傜偩丅偙偺偨傔丄俬俛偼侾倣俙偱偼側偔丄偦偺俁攞偔傜偄偺俁倣俙棳偟偰傗傜側偔偰偼側傜側偄
偙偺乽俁攞乿摍偺乽倛俥俤偺尭彮傪曗偆攞棪乿傪乽僆乕僶乕僪儔僀僽乿偲屇傇丄偮傑傝丄偙偺応崌倛俥俤偑俁暘偺侾偵側傞偲峫偊偰乽俁攞偺僆乕僶乕僪儔僀僽傪妡偗偰偄傞乿偲尵偆丅
- 僩儔儞僕僗僞偵揹棳偑棳傟偰偄傞偲偒丄倁俠俤偼奣偹侽丏俈倁掱搙偱偁傞
- 揹尮揹埑偑俁倁偩偐傜丄俼俛偵偼俀丏俁倁偑壛傢傞
- 俀丏俁倁偱俁倣俙棳傟傞掞峈偩偐傜丄俼俛偼俈俇俈兌偲暘偐傞
偲丄尵偆栿偱丄僗僀僢僠儞僌夞楬偱偼丄儀乕僗揹棳俬俛偼扨偵俬俠傪倛俥俤偱妱偭偰媮傔傞偺偱偼側偔丄僆乕僶乕僪儔僀僽傪俁攞掱搙妡偗偰媮傔傞昁梫偑偁傞偺偱偡丅
埆幰俬俠俛俷傪戅帯偡傞
巆擮側偑傜丄忋偺夞楬偵偼晄嬶崌偑偁偭偰丄幚梡偵側傝傑偣傫丅僗僀僢僠傪俷俥俥偵偟偰傕丄摛媴偑嬐偐偵岝偭偰偟傑偺偱偡丅偙傟偱偼丄摛媴傪姰慡偵徚摂偡傞偙偲偑偱偒傑偣傫丅
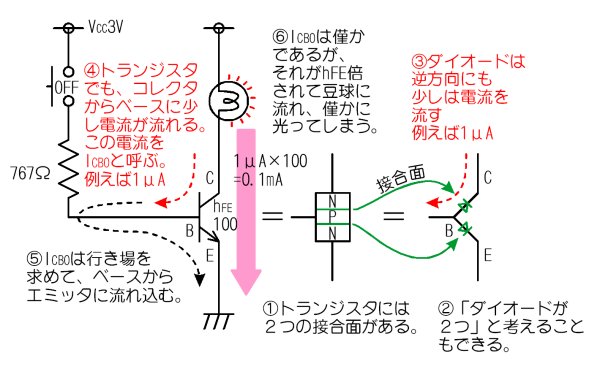
儀乕僗偵棳偡揹棳傪峫偊傞
偦偺棟桼偼師偺傛偆側傕偺偱偡丅
- 僩儔儞僕僗僞偼丄椺偊偽俶俹俶偲俁憌偱峔惉偝傟偰偍傝丄俀偮偺俹俶愙崌柺偑偁傞乮恾偵椢怓偱彂偄偨柺乯
- 偮傑傝丄僟僀僆乕僪傪俀偮崌傢偣偨傕偺偲峫偊傞偙偲傕偱偒傞
- 僟僀僆乕僪偼杮棃丄堦曽岦偩偗偵揹棳傪棳偡偗傟偳丄媡岦偗偵傕彮偟偼揹棳傪楻傜偟偰偟傑偆
- 僩儔儞僕僗僞傕摨偠偱丄僐儗僋僞偐傜儀乕僗傊偼揹棳偼棳傟側偄敜側偺偵丄彮偟偩偗揹棳偑楻傟傞丅偙傟傪俬俠俛俷偲屇傇丅椺偊偽侾兪俙偲偄偆嬐偐側揹棳偩偲偡傞丅
- 俬俠俛俷偼峴偒応傪媮傔偰丄儀乕僗偐傜僄儈僢僞傊偲棳傟崬傓丅
- 儀乕僗偐傜僄儈僢僞偵棳傟崬傫偩揹棳偼倛俥俤攞偝傟偰丄僐儗僋僞偵棳傟偰偟傑偆丅偩偐傜丄俬俠俛俷偼偨偭偨偺侾兪傾儞儁傾偩偭偨偺偵丄摛媴偵偼侽丏侾倣俙偺揹棳偑棳傟丄敄偔岝偭偰偟傑偆丅
偮傑傝丄寵傢傟幰偺揹棳乽俬俠俛俷乿偑埆偝傪偡傞偺偱丄壗偐岺晇傪偟側偄偲丄姰慡偵摛媴傪俷俥俥偱偒側偄栿偱偡丅偪側傒偵丄偙偺揹棳偑俬俠俛俷偺偲屇偽傟傞棟桼偼師偺捠傝偱偡丅
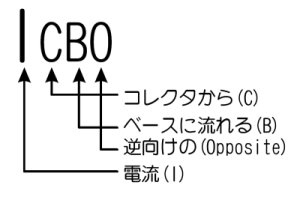
柤慜偺桼棃
偝偰丄偙偺寵傢傟幰偺揹棳揹棳俬俠俛俷傪戅帯偟偰丄僩儔儞僕僗僞傪姰慡偵俷俥俥偵偟偰丄摛媴傪姰慡偵徚摂偡傞偵偼丄儀乕僗乮俛乯偲僄儈僢僞乮俤乯偺娫偵俼俛俤屇偽傟傞掞峈傪庢傝晅偗傑偡丅
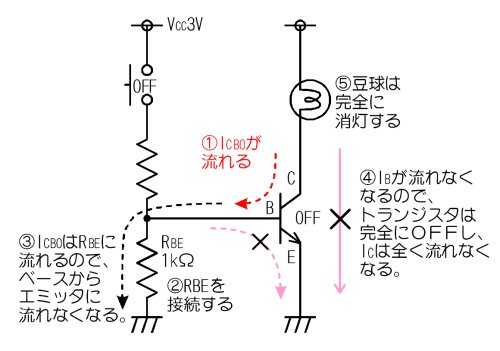
俬俠俛俷傪戅帯偡傞
偮傑傝丄僩儔儞僕僗僞偵傛傞僗僀僢僠儞僌夞楬偱偼丄儀乕僗傪僆乕僾儞偵偡傞偲丄俬俠俛俷偺埆塭嬁偱丄僩儔儞僕僗僞偑姰慡偵俷俥俥偟側偔側傞偨傔丄俼俛俤偲屇偽傟傞掞峈傪儀乕僗偲僄儈僢僞偺娫偵愙懕偡傞偙偲偑昁梫偱偡丅
俼俛俤偺抣偼侾倠兌偔傜偄偐傜丄僩儔儞僕僗僞偵傛偭偰偼丄俀侽倠兌乣俁侽倠兌偱傕戝忎晇偱偡丅
偮傑傝丄俬俠俛俷偵傛偭偰俼俛俤偺椉抂偵敪惗偡傞揹埑偑丄侽丏侾倁掱搙乮僩儔儞僕僗僞傪姰慡偵俷俥俥偱偒傞偔傜偄偺揹埑乯偵側傞傛偆偵愝掕偡傟偽丄椙偄傢偗偱偡丅
椺偊偽俀俽俠侾俉侾俆偱偼俬俠俛俷偼侽丏侾兪俙掱搙偱偡偐傜丄俼俛俤偼侾侽倠兌偱傕戝忎晇偱偡丅
僗僀僢僠儞僌夞楬傪愝寁偡傞
嵟屻偵丄俼俛俤傪庢傝晅偗偰丄姰慡偵俷俥俥偵偱偒傞傛偆偵夵慞偟偨僗僀僢僠儞僌夞楬傪愝寁偡傞庤弴傪峫偊偰尒傑偟傚偆丅
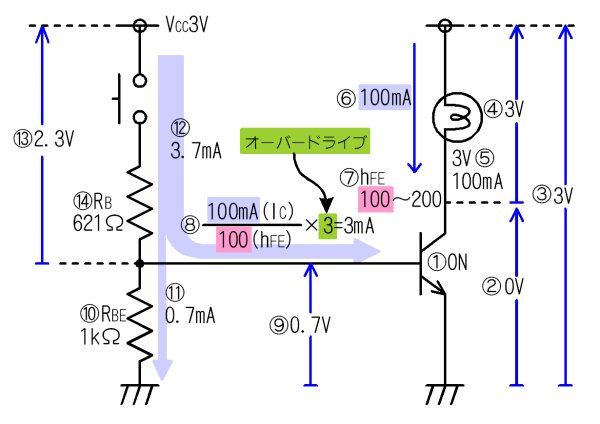
俼俛俤傪巊梡偟偨僗僀僢僠儞僌夞楬偺愝寁
- 摛媴傪岝傜偡偨傔偵丄僩儔儞僕僗僞傪俷俶偵偡傞
- 俷俶偵側偭偨僩儔儞僗僞偺倁俠俤偼侽倁偲側傞丅
- 揹尮揹埑偼俁倁偩偐傜乧
- 摛媴偵偼俁倁偑妡偐傞
- 摛媴偼俁倁侾侽侽倣俙偺傕偺傪巊梡偟偰偄傞偐傜丄
- 僐儗僋僞揹棳偼侾侽侽倣俙棳傟傞丅
- 倛俥俤偼侾侽侽乣俀侽侽偩偑丄揹棳偑晄懌偡傞偲姰慡偵俷俶偟側偔側傞偺偱丄彫偝偄傎偆偺侾侽侽傪巊偭偰愝寁偡傞
- 儀乕僗揹棳偼俬俠傪倛俥俤偱妱偭偰僆乕僶乕僪儔僀僽偺俁傪妡偗傟偽媮傑傝丄俁倣俙偱偁傞丅
- 偲偙傠偱丄僩儔儞僕僗僞偵揹棳偑棳傟偰偄傞偲偒丄倁俛俤偼栺侽丏俈倁偱偁傞
- 俼俛俤偵侾倠兌傪巊梡偡傞偙偲偵偡傞乮俬俠俛俷偼侾兪俙偔傜偄偲峫偊偨乯
- 侾倠兌偵侽丏俈倁偑妡偐偭偰偄傞偺偱丄俼俛俤偵偼侽丏俈倣俙偑棳傟傞丅
- 俼俛偵偼丄儀乕僗揹棳俁倣俙偲偲俬俼俛俤乮俼俛俤偵棳傟傞揹棳乯侽丏俈倣俙偺崌寁偑棳傟傞偺偱丄俬俼俛乮俼俛偵棳傟傞揹棳乯偼俁丏俈倣俙偲側傞丅
- 揹尮揹埑俁倁偱丄倁俛俤偑侽丏俈倁掱搙偩偐傜丄俼俛偵偼丄俀丏俁倁偑妡偐偭偰偄傞丅
- 俀丏俁倁偱俁丏俈倣俙棳傟傞偐傜丄俼俛偺掞峈抣偼俇俀侾兌偲偡傟偽傛偄丅
嬀偺崙乮俶俹俶偲俹俶俹乯乽岺帠拞乿
丂俶俹俶僩儔儞僕僗僞乮俀俽俠倶倶倶偲俀俽俢倶倶倶乯偼椙偔愢柧偵搊応偟傑偡偑丄俹俶俹僩儔儞僕僗僞乮俀俽俙倶倶倶偲俀俽俛倶倶倶乯僩儔儞僕僗僞偼偁傑傝愢柧偝傟傑偣傫丅偟偐偟丄尰幚偵偼慻傒崌傢偣偰巊梡偝傟傑偡偺偱丄峫偊曽偺僐僣傪愢柧偟傑偡丅
愝寁偲帋嶌乮摛揹媴揰摂夞楬乯乽岺帠拞乿
丂僗僀僢僠儞僌夞楬傪墳梡偟偰丄埫偔側傞偲帺摦揑偵摛媴偑揰摂偡傞夞楬傪愝寁偟傑偡丅夞楬偺峔惉偼師偺捠傝丄俠倓俽偵棳傟傞嬐偐側揹棳偱丄俀侽侽倣俙偺揹媴傪俷俶乛俷俥俥偡傞偨傔偵丄僩儔儞僕僗僞傪俀偮巊偭偰僗僀僢僠儞僌偟偰偄傑偡丅
夞楬偺摦嶌乮奣梫乯
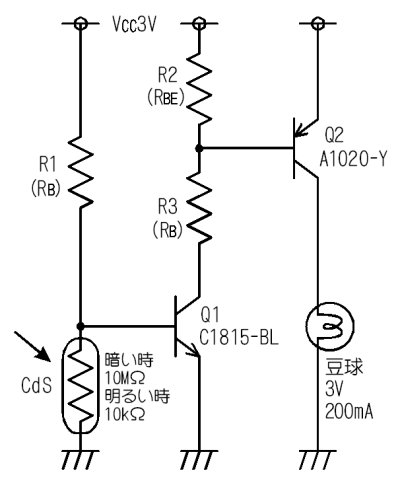
摛揹媴揰摂夞楬
丂柧傞偝傪専抦偡傞偺偼乽俠倓俽乿偲偄偆晹昳偱偡丅棸壔僇僪儈儏僂儉偲偄偆暔幙偑岝偑摉偨傞偲揹棳傪棳偡惈幙傪巊偭偰丄柧傞偝偺曄壔傪掞峈抣偺曄壔偵曄姺偟傑偡丅偙偙偱偼丄埫偄偲偒侾侽俵兌丄柧傞偄偲偒侾侽倠兌偵曄壔偡傞俠倓俽傪巊梡偟偰愝寁偟傑偡丅
摛媴偑揰摂偡傞偲偒乮埫偄帪乯偺夞楬偺摦嶌偼師偺捠傝偱偡丅
- 埫偔側傞偲俠倓俽偺掞峈抣偑侾侽俵僆乕儉偲側傝丄俼侾傪棳傟偨揹棳偼杦偳僩儔儞僕僗僞俻侾偺儀乕僗偵棳傟崬傒傑偡丅
- 偦偺偨傔偵丄俻侾偼俷俶偵側傝丄俼俁傪捠偠偰丄俻俀偺儀乕僗偐傜揹棳傪媧偄弌偟傑偡丅
- 偙傟偵傛偭偰丄俻俀偑俷俶偵側傝丄摛揹媴偵揹棳偑棳傟偰丄揰摂偟傑偡丅
摛媴偑徚摂偡傞偲偒乮柧傞偄帪乯偺夞楬偺摦嶌偼師偺捠傝偱偡丅
- 柧傞偔側傞偲俠倓俽偺掞峈抣偑侾侽倠僆乕儉偲側傝丄俼侾傪棳傟偨揹棳偼杦偳俠倓倱偵棳傟崬傒丄俻侾偺儀乕僗揹棳偼棳傟側偔側傝傑偡丅
- 偦偺偨傔偵丄俻侾偼俷俥俥偲側傝丄俼俁傪捠偠偰俻俀偺儀乕僗偐傜揹棳傪媧偄弌偝側偔側傝傑偡丅
- 偙傟偵傛偭偰丄俻俀偑俷俥俥偵側傝丄摛揹媴偵偼揹棳偑棳傟偢丄徚摂偟傑偡丅
揰摂帪偺忬懺偲掞峈抣偺寛掕
丂偙偺夞楬偼丄摛媴偑揰摂偟偰偄傞偲偒偺忬懺傪峫偊傞偲掞峈抣傪媮傔傞偙偲偑偱偒傑偡丅恾偺嘆嘇嘊乧偺斣崋偑丄売忦彂偒偺斣崋偲懳墳偟偰傑偡偐傜丄尒斾傋側偑傜峫偊偰偔偩偝偄丅
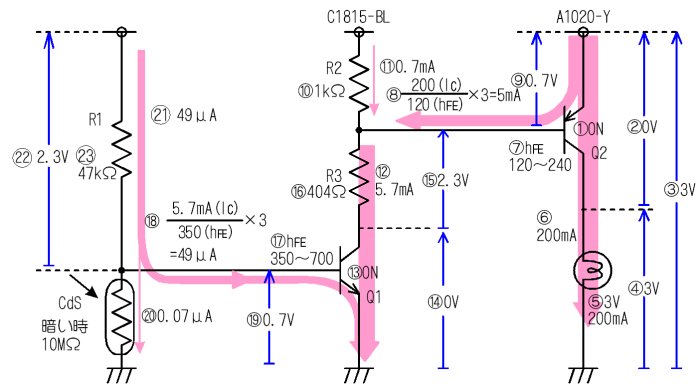
掞峈抣偺寛掕
- 摛媴傪揰摂偡傞偨傔偵偼丄俻侾偼俷俶偵偡傞
- 俷俶偵側偭偰俻侾偺倁俠俤偼侽倁偵側傞
- 揹尮揹埑偼俁倁偩偐傜
- 摛媴偵偼俁倁偑壛傢傞
- 俁倁丄俀侽侽倣俙偺摛媴傪巊偭偰偄傞偐傜
- 俻俀偺僐儗僋僞偵偼俀侽侽倣俙偺揹棳偑棳傟傞
- 巇條彂傛傝丄俻俀偺倛俥俤偼侾俀侽乣俀係侽偲側偭偰偄傞偑丄揹棳偺晄懌偱姰慡偵俷俶偟側偄偲崲傞偺偱丄彫偝偄傎偆偺侾俀侽傪寁嶼偵巊偆丅
- 俬俠傪倛俥俤偱妱偭偰丄僆乕僶乕僪儔僀僽乮俁乯傪妡偗傞偲丄儀乕僗揹棳俆倣俙偑媮傑傞
- 揹棳偺棳傟偰偄傞僩儔儞僕僗僞偺倁俛俤偼栺侽丏俈倁偱偁傞丅
- 俼俀偼俬俠俛俷偺埆塭嬁傪旔偗傞偨傔偺俼俛俤偱偁傞丅俙侾侽俀侽偱偼俬俠俛俷偑侾兪俙偁傞偺偱丄侾兪俙偑棳傟偰傕侽丏侾倁乮愨懳偵俬俛偑棳傟側偄揹埑乯偟偐揹埑偑惗偠側偄傛偆偵峫偊偰丄俼俀偺抣偼侾倠兌偲偡傞
- 侾倠兌偺俼俀偵丄倁俛俤偺侽丏俈倁偑壛傢偭偰偄傞偐傜丄俼俀偵偼丄侽丏俈倣俙偺揹棳偑棳傟傞
- 俼俁偵偼丄俼俀偐傜侽丏俈倣俙偑丄俻俀偐傜俆倣俙偑棳傟崬傓偺偱丄崌寁俆丏俈倣俙偺揹棳偑棳傟傞丅
- 俻侾傕俷俶偟偰偄傞偼偢偩偐傜丄
- 俻侾偺倁俠俤偼侽倁偵側傞丅
- 俼俁偵壛傢傞揹埑偼丄揹尮揹埑偺俁倁偐傜丄俻俀偺倁俛俤偲俻侾偺倁俠俤傪堷偄偨傕偺偲側傝丄俀丏俁倁偱偁傞丅
- 俀丏俁倁壛傢偭偰丄俆丏俈倣俙棳傟傞偺偩偐傜丄俼俁偺抣偼係侽係兌偲偡傞丅
- 俻侾偺倛俥俤偼俁俆侽乣俈侽侽偱偁傞偑丄姰慡偵俷俶偵偡傞偨傔偵丄掅偄傎偆偺俁俆侽傪巊梡偟偰愝寁偡傞
- 僐儗僋僞揹棳俁丏俈倣俙傪倖俥俤俁俆侽偱妱偭偰丄僆乕僶乕僪儔僀僽偺俁傪妡偗傞偲丄儀乕僗揹棳偺係俋兪俙偑媮傑傞丅
- 僩儔儞僕僗僞偵揹棳偑棳傟偰偄傞偲偒丄倁俛俤偼奣偹侽丏俈倁偱偁傞丅
- 埫偄偲偒俠倓俽偺掞峈抣偼侾侽俵兌偲崅偔丄侽丏俈倁妡偐偭偰傕棳傟傞揹棳偼丄侽丏侽俈兪俙偱偁傞
- 俼侾偵偼丄俻侾偺儀乕僗揹棳乮係俋兪俙乯偲俠倓俽偺揹棳乮侽丏侽俈兪俙乯偑崌傢偝偭偰棳傟傞丅偟偐偟丄俠倓俽偺揹棳偼儀乕僗揹棳偵斾傋偰廫暘偵彫偝偄偺偱柍帇偱偒丄俼侾偵偼丄係俋兪俙偑棳傟傞
- 揹尮揹埑偑俁倁丄俻侾偺倁俛俤偑侽丏俈倁偩偐傜丄俼侾偵偼俀丏俁倁偑壛傢偭偰偄傞丅
- 俀丏俁倁壛傢偭偰丄係俋兪俙偺揹棳偑棳傟傞偺偩偐傜丄俼侾偺抣偼係俈倠兌偲偡傞丅
徚摂帪偺忬懺
丂廃埻偑埫偔側傝丄俠倓俽偺掞峈抣偑侾侽倠兌偵側傞偲丄摛媴偑徚摂偡傞偐丄峫偊偰傒傑偡丅
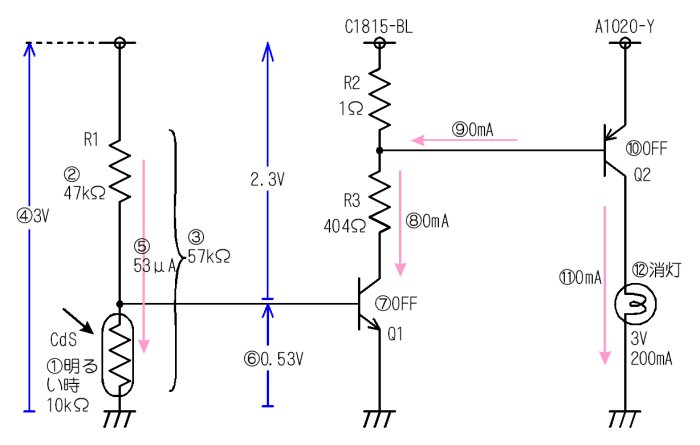
掞峈抣偺寛掕
- 廃埻偑柧傞偔側傞偲丄俠倓俽偺掞峈抣偼侾侽倠兌偵壓偑傞
- 俼侾偼係俈倠兌偱偁傞丅
- 偩偐傜丄俠倓俽偲俼侾値倧捈楍崌惉掞峈偼侾侽倠亄係俈倠偱丄俆俈倠兌偱偁傞丅
- 偙偙偵揹尮揹埑俁倁偑壛傢偭偰偄傞偐傜丄
- 俠倓俽偵偼丄俆俁兪俙偺揹棳偑棳傟傞
- 廬偭偰丄侾侽倠兌偺俠倓俽偵偼丄侽丏俆俁倁偺揹埑偑敪惗偡傞
- 壏搙側偳偺忦審偵傕傛傞偑丄俻侾偺儀乕僗揹埑偑侽丏俆俁倁偱偁傟偑丄俻侾偼俷俥俥偲側傞丅
壏搙偑崅偔側傞偲倁俛俤偺抣偑掅壓偡傞偺偱丄幒撪偺徠柧偔傜偄偱偼丄姰慡偵俻侾偑俷俥俥偟側偄壜擻惈傕偁傞丅
偦偺傛偆側応崌偼丄俼侾傪侾侽侽倠兌偵曄偊偰傗傞偲丄偦傟傎偳嫮偔側偄岝偱傕俷俥俥偡傞傛偆偵側傞丅
偙偺偲偒丄俻侾偺僆乕僶乕僪儔僀僽偼侾丏俆掱搙偟偐妋曐偱偒偰偄側偄偑丄侾俉侾俆偼倛俥俤偺儕僯傾儕僥傿偑崅偔丄僆乕僶乕僪儔僀僽侾丏俆偱傕丄偙偺峔惉偺夞楬側傜丄廫暘枮懌側掱搙偵俷俶偡傞偙偲偑偱偒傞丅
- 偦偺寢壥俻侾偺僐儗僋僞揹棳偼侽倣俙偲側傞丅
- 摉慠丄俻俀偺儀乕僗揹棳傕侽倣俙偲側傞丅
- 偦偺寢壥俻侾偼俷俥俥偲側傝丄
- 摛媴偵棳傟傞揹棳偼侽倣俙偲側傝丄
- 揹媴偼徚摂偡傞
嶌偭偰傒傛偆
愝寁抣偲幚應抣偺堘偄
乽捠傝偵偔偝乿偲乽偲偍傝堈偝乿
丂掞峈傪攦偆偲偒偼丄椺偊偽乽俀俀侽兌偺掞峈傪壓偝偄乿丄偲偄偆傛偆偵丄乽掞峈乿偺抣偱屇傃傑偡丅偟偐偟丄偦偺媡悢偺乽僐儞僟僋僞儞僗乿偱昞偡偙偲傕偱偒傑偡丅
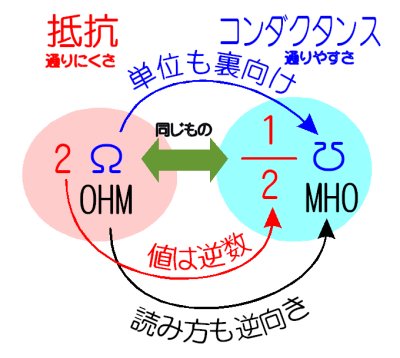
掞峈偲僐儞僟僋僞儞僗
丂掞峈偲僐儞僟僋僞儞僗偼師偺娭學偵偁傝傑偡丅掞峈偼乽揹棳偺捠傝偵偔偝乿丄僐儞僟僋僞儞僗偼乽揹棳偺捠傝傗偡偝乿傪偁傜傢偟丄偍屳偄偵媡悢偺娭學偵偁傝傑偡丅
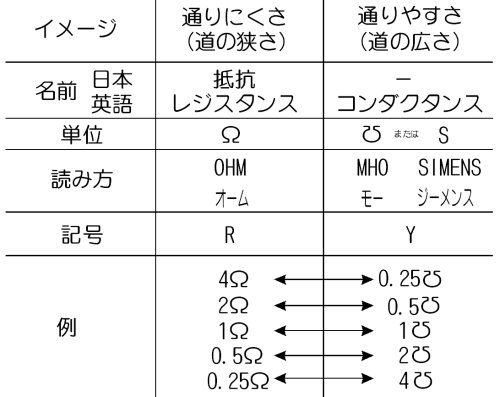
掞峈偲僐儞僟僋僞儞僗
丂掞峈[兌](OHM)偺偑媡悢偑丄僐儞僟僋僞儞僗[傂](MHO)偲偄偆偺偼丄抣偑媡悢側傜丄扨埵偺婰崋傕忋壓媡丄撉傒曽傕媡偝傑丄偲偄偆傆偆偵丄偲偰傕垽沢偑偁偭偨偺偱偡偑丄怴偟偄扨埵宯偱偼丄掞峈[S](SIMENS)傪巊偆偙偲偵側傝傑偟偨丅
丂偟偐偟丄暘偐傝堈偔煭棊傕棙偄偰偄傞偺偱丄偙偺儁乕僕偱偼乽兌乿偲乽傂乿傪巊偄傑偡丅兌傪忋壓媡偝傑偵偟偨婰崋偼僥僉僗僩偱昞帵偱偒側偄偺偱丄傂傜偑側偺乽傂乿傪巊偄傑偡丅
扤偱傕抦偭偰傞捈楍崌惉掞峈
丂俀杮偺掞峈傪捈楍偵偮側偖偲丄俀杮偺掞峈偺抣傪懌偟偨傕偺偵側傝傑偡丅
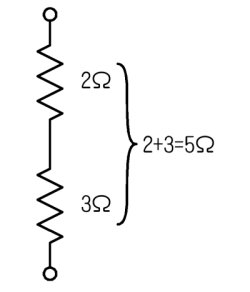
捈楍崌惉掞峈
岞幃側傜抦偭偰傞暲楍崌惉掞峈
丂俀杮偺掞峈傪暲楍偵偮側偄偩偲偒偺抣偼丄壓偺岞幃偱媮傔傞偙偲偑偱偒傑偡丅
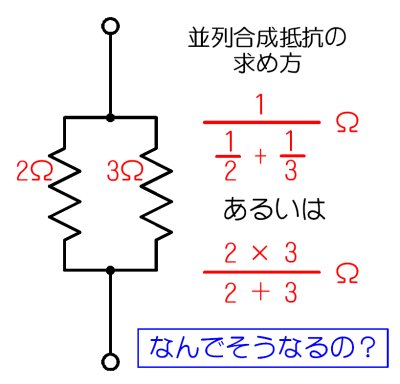
暲楍崌惉掞峈偺岞幃
丂偟偐偟丄偦偺棟桼偼暘偐傝傑偡偐丠
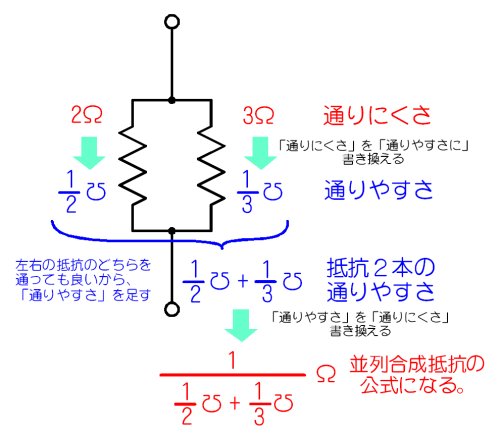
捈楍崌惉掞峈
- 傑偢丄嵍塃偺掞峈偺乽捠傝偵偔偝[兌]乿傪乽捠傝傗偡偝[傂]乿偵抲偒姺偊傑偡丅
- 揹棳偼丄塃偺掞峈傪捠傞偙偲傕丄嵍偺掞峈傪捠傞偙偲傕偱偒傑偡偐傜丄暲楍掞峈偺乽捠傝傗偡偝乿偼嵍塃偺掞峈偺乽捠傝傗偡偝乿傪懌偟偨傕偺偵側傝傑偡丅
- 嵍塃偺掞峈偺崌惉掞峈丄偮傑傝丄乽捠傝偵偔偝乿傪抦傝偨偗傟偽丄忋偱媮傔偨乽捠傝傗偡偝乿傪媡悢偵偟偰丄乽捠傝偵偔偝乿偵曄姺偟傑偡丅
- 偡傞偲丄娵妎偊偟偰偄傞暲楍崌惉掞峈偺岞幃偵側偭偰偄傑偡丅
暲楍崌惉掞峈偺墶拝側彂偒曽
丂暲楍掞峈傪寁嶼偡傞偵偼丄暘悢偺暘悢偑弌偰偔傞偺偱丄彂偔偺偑柺搢偱偡丅偦偙偱丄乽//乿偲偄偆婰崋傪巊偭偰丄暲楍掞峈偺寁嶼傪娙扨偵昞偡偙偲偑偱偒傑偡丅
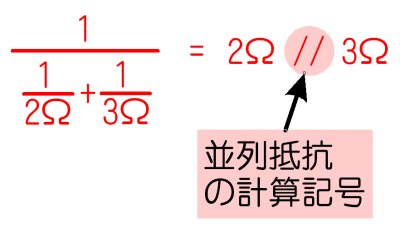
捈楍崌惉掞峈
岎棳偲偦偺廃婜傗廃攇悢
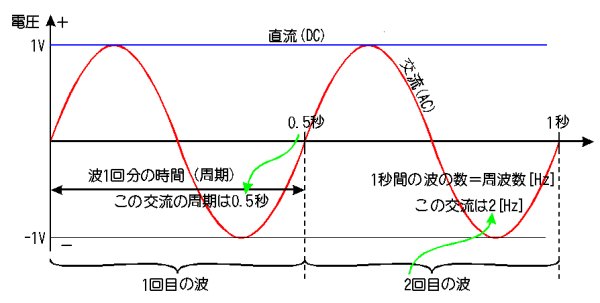
丂廃婜揑偵岦偒傗戝偒偝偑曄壔偡傞揹埑傗揹棳傪乽岎棳乿偲屇傃傑偡丅壓偺恾偱尵偊偽丄惵慄偑侾倁偺捈棳丄愒慄偑岎棳乮拲堄丗侾倁偺岎棳偱偼偁傝傑偣傫傛乯偱偡丅
岎棳揹埑偲揹棳偺恾帵
丂岎棳偑孞傝曉偡懍偝偼乽廃婜乿乮攇堦夞暘偺帪娫乯傗丄廃攇悢乮侾昩娫偵傗偭偰偔傞攇偺夞悢乯偱昞偟傑偡丅忋偺恾偱偼丄攇堦夞偺帪娫偑侽丏俆昩側偺偱丄廃婜侽丏俆[昩]丄偁傞偄偼丄廃婜俆侽侽[倣倱]乮儈儕僙僇儞僪乯偱偡丅傑偨丄堦昩娫偵俀夞攇偑傗偭偰棃傞偺偱丄廃攇悢偼俀[俫倸]乮僿儖僣乯偱偡丅
岎棳偺戝偒偝
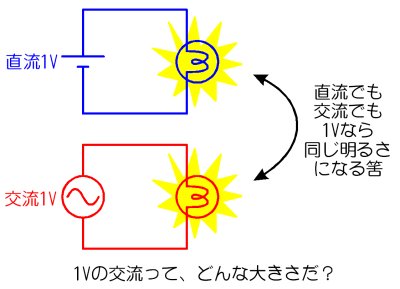
丂侾倁偺岎棳偲偼偳偺傛偆側岎棳偱偟傚偆偐丅摨偠乽侾倁乿偲屇傇偐傜偵偼丄岎棳偺侾倁傕丄捈棳偺侾倁偲摨偠埿椡偑偁傞敜偱偡丅偦偙偱丄師偺恾偺傛偆側幚尡傪偟偰傒傑偟偨丅
捈棳偺侾倁偲岎棳偺侾倁
丂偦偺偲偒偺岎棳偺戝偒偝傪挷傋傞偲丄壓偺恾偺傛偆偵側偭偰偄傑偟偨丅
侾倁偺岎棳
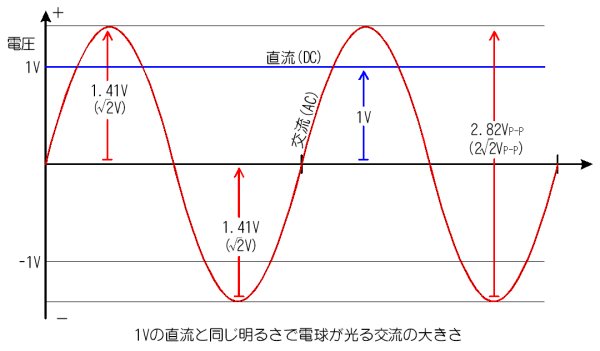
丂侾倁偺岎棳乮俙俠侾倁丄傑偨偼丄侾倁俙俠乯偺堦斣崅偄揹埑偼侾丏係侾倁丄堦斣掅偄揹埑偼亅侾丏係侾倁丄扟偺掙偐傜嶳偺捀忋傑偱偺偱傫偁偮偼丄俀丏俉俀倁偲側偭偰偄傑偡丅
丂惓妋偵偼丄侾倁偺岎棳偺嵟戝揹埑偼亄併俀倁丄嵟掅揹埑偼亅併俀倁偵側傝傑偡丅
丂扟偺掙偐傜丄嶳偺捀忋傑偱偺揹埑偺偱岎棳偺戝偒偝傪屇傇偙偲偑椙偔偁傝傑偡丅應掕偟堈偄偐傜偱偡丅偦偺応崌丄俀丏俉俀倁俹亅俹乮僺乕僋丒僩僁丒僺乕僋)偲乽俹亅俹乿偺婰崋傪屻傠偵晅偗偰屇傃傑偡丅
丂偮傑傝丄侾倁偺捈棳偲摨偠柧傞偝偱摛揹媴傪岝傜偣傞偙偲偑弌棃傞偺偼丄俙俠侾倁偺岎棳偱丄暿偺尵偄曽偱偼丄俀丏俉俀倁俹亅俹偺岎棳偱偡丅
侾倁偺岎棳
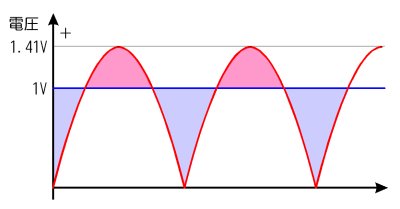
丂侾倁偺岎棳偺嵟戝揹埑偑丄侾丏係侾倁偲侾倁傛傝崅偔側傞偺偼側偤偱偟傚偆丅岎棳偺儅僀僫僗晹暘傪忋偵愜傝曉偟偰丄捈棳偲偔傜傋偰傒傞偲椙偔暘偐傝傑偡丅
丂忋偺恾偱惵偵揾傝偮傇偟偨晹暘偱偼岎棳偑捈棳傛傝彫偝偔側偭偰偄傑偡丅偙偺晧偗偨暘傪岎棳偼偳偙偐偱庢傝栠偝側偔偰偼側傝傑偣傫丅偦偙偱丄愒偵揾傝偮傇偟偨晹暘偱捈棳傛傝崅偔側傞偙偲偱丄惵偔揾傝偮傇偟偨晹暘偱晧偗偨暘傪庢傝曉偟偰丄摨偠埿椡傪弌偟偰偄傞傢偗偱偡丅
岎棳揹埑偲揹棳偺恾帵
丂岎棳偺揹埑偲揹棳偼攇慄偱恾帵偟傑偡丅乮偟偐偟丄巹偺巊偭偰偄傞僣乕儖偼攇慄傪彂偔婡擻偑側偔丄攇慄傪彂偔偵偼丄偲偰偮傕側偔庤娫偑偐偐傞偺偱丄搑拞偱嵙愜偟偰丄岎棳傪揰慄偱恾帵偡傞偙偲偵側傞偐傕偟傟傑偣傫丅
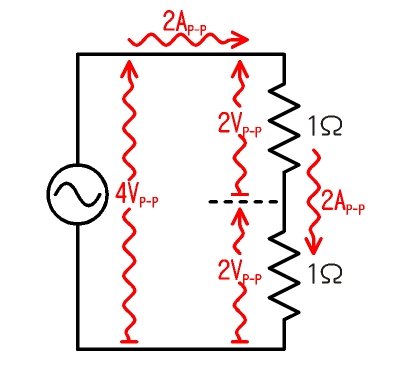
岎棳揹埑偲揹棳偺恾帵
億僀儞僩偼
- 岎棳揹埑偲揹棳傪攇慄栴報偱昞偟傑偡
- 岎棳揹埑偲揹棳傪偺婰崋傪嬫暿偡傞偨傔偵丄揹埑偺栴報偼偍怟偵墶朹傪晅偗傑偡
揹埑傪椉曽偵栴偠傝偺偮偄偨婰崋偱昞婰偡傞曽朄偑偁傝傑偡偑丄偙傟偱偼揹埑偺曽岦偑暘偐傜側偄偐傜偱偡丅
- 庡偵岎棳偺戝偒偝偼僺乕僋丒僩僁丒僺乕僋抣乮屻偱愢柧偟傑偡乯偱帵偟傑偡
岎棳偲捈棳偑摨帪偵棳傟傞夞楬
丂壓恾偺傛偆側夞楬傪峫偊傑偟傚偆丅岎棳乮俇倁俹亅俹乯偲捈棳乮俁倁乯偑椉曽壛傢偭偰偍傝丄捈棳偲岎棳偑摨帪偵棳傟偰偄傑偡丅
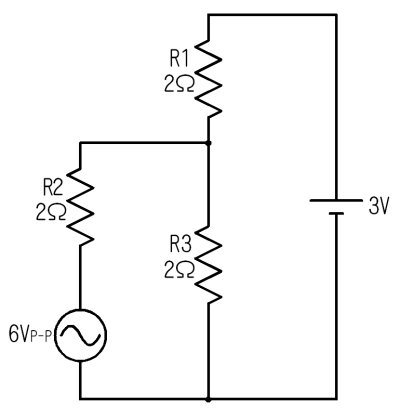
岎棳偲捈棳偑摨帪偵棳傟傞夞楬
丂峫偊曽偺億僀儞僩偼堦偮両丅捈棳偲岎棳偼暿乆偵峫偊傞丅偮傑傝丄乽捈棳傪峫偊傞偲偒偼岎棳偺帠偼朰傟丄岎棳偺偙偲傪峫偊傞偲偒偼捈棳偺偙偲傪朰傟傞乿偲偄偆偙偲偱偡丅
捈棳偵偮偄偰峫偊傞乮岎棳偺偙偲偼朰傟傞乯
丂傑偢丄岎棳偺偙偲偼朰傟丄捈棳偺偙偲偩偗峫偊偰尒傑偟傚偆丅岎棳偺帠偼朰傟傞偺偱偡偐傜丄俇倁俹亅俹偺岎棳揹埑尮偑偁偭偰傕僔僇僩偟偰丄偨偩偺揹慄偩偲峫偊傑偡丅
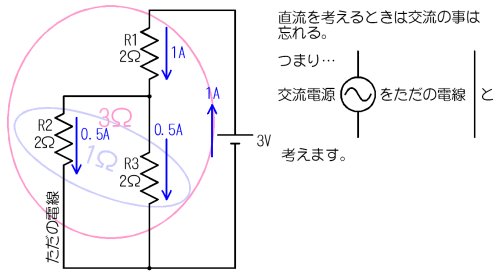
捈棳偩偗峫偊偨夞楬乮岎棳偼柍帇乯
丂偦偆偡傞偲丄俼俀偲俼俁偼暲楍偱丄侾兌丄偦偙偵俼侾偑捈楍偵宷偑偭偰偄傑偡偐傜丄慡懱偺崌惉掞峈偼俁兌偲側傝傑偡丅偦偺偨傔丄夞楬慡懱偵偼侾俙丄偦偟偰丄俼侾偵偼侾俙丄俼俀偲俼俁偵偼侽丏俆俙偺捈棳揹棳偑棳傟傑偡丅
岎棳偵偮偄偰峫偊傞乮捈棳偺偙偲偼朰傟傞乯
丂師偵丄捈棳偺偙偲偼朰傟丄岎棳偺偙偲偩偗峫偊偰尒傑偟傚偆丅捈棳偺帠偼朰傟傞偺偱偡偐傜丄俁倁偺捈棳揹埑尮偑偁偭偰傕僔僇僩偟偰丄偨偩偺揹慄偩偲峫偊傑偡丅
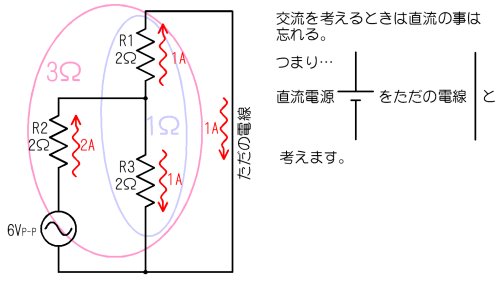
岎棳偩偗峫偊偨夞楬乮捈棳偼柍帇乯
丂偦偆偡傞偲丄俼侾偲俼俁偑暲楍偱丄侾兌偲側傝丄偙傟偵丄俼俀偑捈楍偵宷偑偭偰偄傑偡偐傜丄慡懱偺崌惉掞峈偼俁兌偲側傝傑偡丅偦偺偨傔丄夞楬慡懱偵偼俀俙俹亅俹偺岎棳偑棳傟丄俼俀偵傕俀俙俹亅俹丄俼侾偲俼俁偵偼丄侾俙俹亅俹偺揹棳偑棳傟傑偡丅
捈棳偲岎棳傪崌懱偝偣偰傒傞
丂偙偺傛偆偵丄暿乆偵峫偊偨捈棳偲岎棳偺棳傟曽傪丄堦偮偺恾偵傑偲傔偰傒傑偟傚偆丅
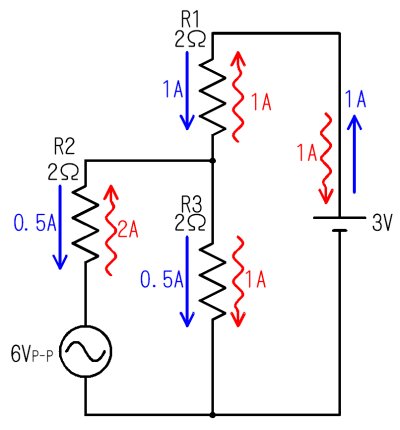
捈棳偲岎棳偺棳傟曽
丂岎棳偲捈棳偼丄偍屳偄姳徛偡傞偙偲側偔丄戝偒偝傗岦偒傕帺桼婥傑傑偵丄撈棫偟偨傕偺偲偟偰棳傟偰偄傞偙偲偑暘偐傝傑偡丅
岎棳傪埖偆僩儔儞僕僗僞夞楬
丂偦傟偱偼丄捈棳偲岎棳偺椉曽偑棳傟傞僩儔儞僕僗僞夞楬偺摦嶌傪峫偊偰尒傑偟傚偆丅壓恾偺憹暆夞楬偱捈棳弌椡揹埑倁倧倧偲怣崋乮岎棳乯弌椡揹埑倴倧丄捈棳擖椡揹棳俬俛俛偲怣崋乮岎棳乯擖椡揹棳倝倐傪媮傔傑偡丅
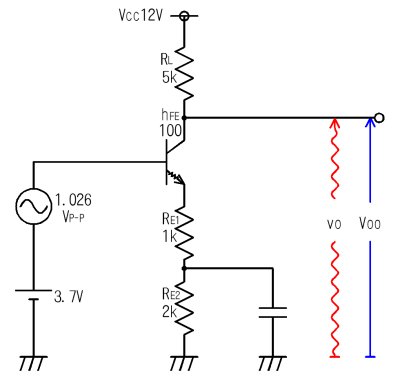
捈棳偲岎棳偺棳傟傞僩儔儞僕僗僞夞楬
丂捈棳偲岎棳偺椉曽偑棳傟傞夞楬傪峫偊傞億僀儞僩偼乽捈棳偲岎棳偼暿乆偵峫偊傞乿偱偟偨偹丅
捈棳偵偮偄偰峫偊傞乮岎棳偺偙偲偼朰傟傞乯
丂傑偢丄岎棳偺偙偲偼朰傟丄捈棳偺偙偲偩偗峫偊偰尒傑偟傚偆丅岎棳偺帠偼朰傟傞偺偱偡偐傜丄侾丏侽俀俇倁俹亅俹偺岎棳擖椡偑偁偭偰傕僔僇僩偟偰丄嵟弶偼偨偩偺揹慄偩偲峫偊傑偡丅傑偨丄僐儞僨儞僒偼捈棳傪捠偟傑偣傫偐傜丄偙傟傕僔僇僩偱偡丅
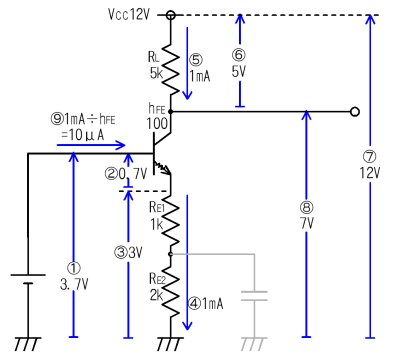
捈棳偲岎棳偺棳傟傞僩儔儞僕僗僞夞楬
- 僩儔儞僕僗僞偺儀乕僗偵偼俁丏俈倁偺揹埑偑妡偭偰偄傑偡丅
- 捠忢偵摦嶌偟偰偄傞僩儔儞僕僗僞偺倁俛俤偼侽丏俈倁掱搙偱偡
- 偙偺偨傔丄俼俤侾偲俼俤俀乮崌傢偣偰俁倠兌乯偵偼俁倁偺揹埑偑壛傢傝傑偡丅
- 偦偺寢壥丄俼俤侾偲俼俤俀偵偼侾倣俙偺揹棳偑棳傟傑偡丅偮傑傝丄僄儈僢僞捈棳揹棳俬俤俤偼侾倣俙偲側傝傑偡丅
- 俬俤俤偑侾倣俙偲側傟偽丄俬俠俠傕侾倣俙偲側傝傑偡丅
- 侾倣俙偺俬俠俠偵傛偭偰丄俆倠兌偺俼俴偵偼倁俼俴亖俆倁偺揹埑偑敪惗偟傑偡丅
- 揹尮揹埑偼侾俀倁偱偡丅
- 弌椡捈棳揹埑倁倧倧偼揹尮揹埑偺侾俀倁偐傜丄倁俼俴偺俆倁壓偑偭偨揹埑偱偡偐傜丄侾俀亅俆亖俈倁偲側傝傑偡
- 儀乕僗偵棳傟崬傓捈棳揹棳俬俛俛偼俬俠俠亐倛俥俤側偺偱丄侾侽兪俙偲側傝傑偡丅
岎棳偵偮偄偰峫偊傞乮捈棳偺偙偲偼朰傟傞乯
丂師偵丄捈棳偺偙偲偼朰傟丄岎棳偺偙偲偩偗峫偊偰尒傑偟傚偆丅捈棳偺帠偼朰傟傞偺偱偡偐傜丄俁丏俈倁偺捈棳揹埑尮偑偁偭偰傕僔僇僩偟偰丄偨偩偺揹慄偩偲峫偊傑偡丅
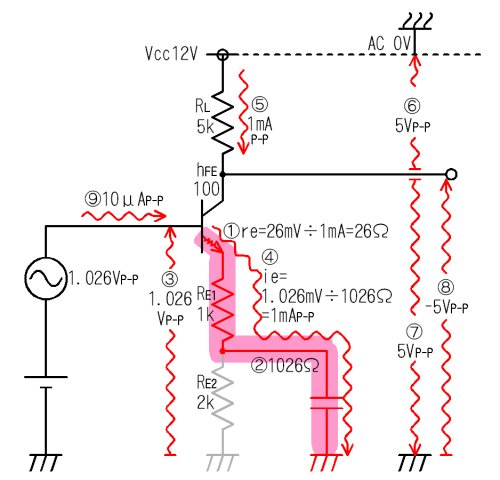
岎棳偩偗傪峫偊偨夞楬乮捈棳偼柍帇乯
- 僄儈僢僞摍壙僀儞僺乕僟儞僗倰倕偼俀俇倣倁亐俬俤俤偱寁嶼偱偒丄偙偺応崌丄俀俇兌偲側傝傑偡丅
偙偺乽俀俇倣倁乿偼墌廃棪偑乽俁丏侾係乿偱偁傞偺偲摨條偺掕悢偱丄夞楬偺揹埑傗揹棳偵塭嬁偝傟偢乮僔儕僐儞僶僀億乕儔僩儔儞僕僗僞側傜乯偄偮傕摨偠偱偡丅
- 僐儞僨儞僒偼岎棳傪姰慡偵捠偟傑偡偐傜丄僄儈僢僞偺怣崋揹棳倝倕偼俼俤俀偵偼棳傟偢丄恾偵愒偱帵偡宱楬傪捠傝傑偡丅偮傑傝丄儀乕僗偺棤懁偐傜丄倰倕傪捠傝丄俼俤侾偲僐儞僨儞僒傪宱桼偟偰傾乕僗傊岦偐偄傑偡丅偱偡偐傜丄僄儈僢僞懁偺僀儞僺乕僟儞僗偼俀俇兌亄侾倠兌偱侾侽俀俇兌偱偡丅
- 儀乕僗偵偼侾丏侽俀俇倣倁俹亅俹偺怣崋揹埑偑壛傢偭偰偄傑偡丅
- 儀乕僗怣崋揹埑乮侾丏侽俀俇倣倁乯偲丄僄儈僢僞懁偺僀儞僺乕僟儞僗乮侾侽俀俇兌乯偐傜僆乕儉懃偵傛傝丄僄儈僢僞怣崋揹棳偑寛傑傝傑偡丅
倝倕亖儀乕僗怣崋揹埑亐僄儈僢僞懁僀儞僺乕僟儞僗
丂亖侾丏侽俀俇倁俹亅俹亐侾侽俀俇兌
丂亖侾倣俙俹亅俹
偲側傝傑偡丅
- 僐儗僋僞偵傕倝倕偲摨偠侾倣俙俹亅俹揹棳偑棳傟傑偡丅
- 俆倠兌偺俼俴偵侾倣俙俹亅俹偺俬俼俴偑棳傟傞偺偱丄俆倁俹亅俹偺揹埑偑惗偠傑偡丅
- 偲偙傠偱丄揹尮傕岎棳偐傜尒傟偽侽倁偱偡偐傜丄傾乕僗偲弌椡抂巕偺娫偵傕俆倁俹亅俹偺揹埑偑惗偠傑偡丅偟偐偟丄栴報偑壓傪岦偄偰偄傑偡丅
- 偦偙偱丄栴報傪忋岦偗偵捈偡偲弌椡怣崋揹埑偼亅俆倁俹亅俹偲媮傔傜傟傑偡丅
怣崋乮岎棳)惉暘傪栺俆攞偵憹暆偟偰偄傑偡偹丅偙偺憹暆棪偼丄俼俴乛乮倰倕亄俼俤侾乯偱媮傑傞偺偱偡丅
- 傑偨丄儀乕僗偵棳傟傞怣崋揹棳倝倐偼丄僐儗僋僞怣崋揹棳倝們亐倛俥俤亖侾侽兪俙偲暘偐傝傑偡丅
捈棳偲岎棳傪崌懱偝偣偰傒傞
丂偙偺傛偆偵丄暿乆偵峫偊偨捈棳偲岎棳偺棳傟曽傪丄堦偮偺恾偵傑偲傔偰傒傑偟傚偆丅
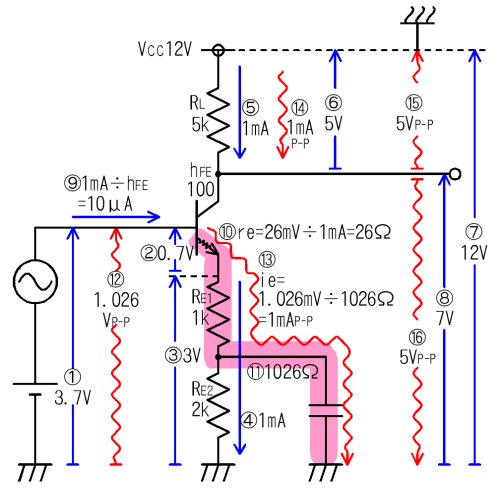
捈棳偲岎棳傪慡晹彂偄偰傒偨
丂旕忢偵傗傗偙偟偔側偭偰偟傑偄傑偟偨丅傗偼傝丄捈棳偲岎棳偼暘偗偰峫偊偨傎偆偑傛偄偱偡偹丅
丂偝偰丄弌椡抂巕偵偼丄俈倁偺捈棳偲俆倁俹亅俹偺岎棳偑摨帪偵尰傟傑偡偐傜丄壓偺恾偵愒慄偱帵偡傛偆側丄俈倁傪拞怱偵丄忋壓偵俀丏俆倁偢偮忋壓偡傞揹埑偑弌偰偒傑偡丅岎棳偺戝偒偝偼栺俆攞偵憹暆偝傟偰偄傑偡丅偙偺憹暆棪偺俆攞偼丄奣偹俼俴亐俼俤侾亖俆倠亐侾倠偱媮傔傞偙偲偑偱偒傑偡丅
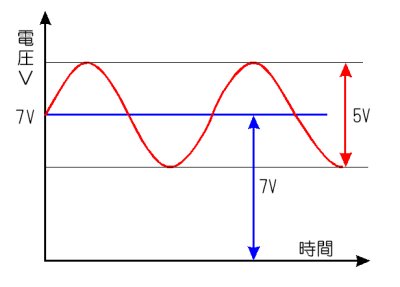
弌椡抂巕偺揹埑倁俷偺僌儔僼
僄儈僢僞僼僅儘傾乽岺帠拞乿
丂僄儈僢僞偐傜弌椡傪庢傝弌偡憹暆婍偱丄戝偒側揹棳傪弌椡偡傞偙偲偑偱偒傑偡丅
擖椡僀儞僺乕僟儞僗偲偼
丂偁傞夞楬偺擖椡偺岎棳掞峈偑偳偺偔傜偄偁傞偐丠偲偄偆偙偲偱偡丅偮傑傝丄壓偺恾偱丄愒怓偱帵偡倅倝偺抣偑壗兌偐丄偲偆偙偲偱偡丅
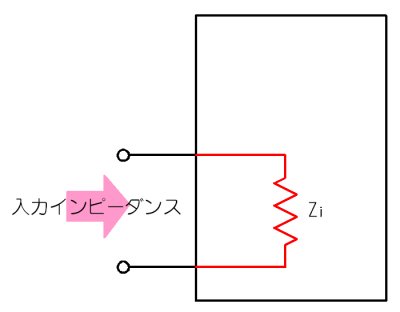
擖椡僀儞僺乕僟儞僗偲偼
丂應掕偺巇曽偼娙扨偱丄岎棳怣崋倴倝傪壛偊偰丄棳傟偨岎棳怣崋揹棳倝倝傪應掕偟丄擖椡僀儞僺乕僟儞僗倅倝偼
倅倝亖倴倝乛倝倝
偱媮傔傑偡丅
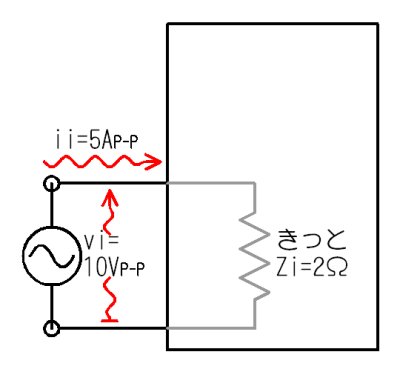
擖椡僀儞僺乕僟儞僗傪應掕偡傞
偙偺椺偱偼乧
倅倝亖侾侽倁俹亅俹亐俆俙俹亅俹亖俀兌
偲側傝傑偡丅
夞楬恾偐傜擖椡僀儞僺乕僟儞僗傪媮傔傞
丂幚偼丄愭傎偳偺夞楬丄僼僞傪奐偗偰傒傞偲丄師恾偺傛偆側攝慄偵側偭偰偄傑偟偨丅偝偰丄夞楬偐傜擖椡僀儞僺乕僟儞僗傪媮傔偰傒傑偟傚偆丅
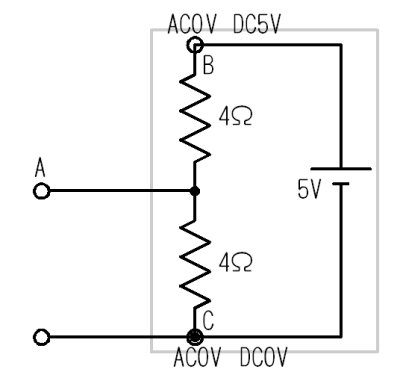
撪晹偺夞楬
丂俠揰偺俢俠揹埑偼侽倁偮傑傝丄傾乕僗偱偡丅傑偨丄俙俠揹埑傕侽倁偮傑傝丄岎棳偱尒偰傕傾乕僗偝傟偰偄傑偡丅
丂偱偼丄俛揰偼偳偆偱偟傚偆偐丄俢俠揹埑偼俆倁丄柧傜偐偵傾乕僗偱偼偁傝傑偣傫丅偟偐偟丄俙俠揹埑偼侽倁丄岎棳偱尒傞偲傾乕僗側偺偱偡丅
丂偮傑傝丄捈棳偲岎棳偼慡偔暿暔偲峫偊傞偺偱丄俛揰偵偼捈棳偺俆倁妡偭偰偄傑偡偑丄岎棳偐傜尒傟偽傾乕僗偲側傝傑偡丅
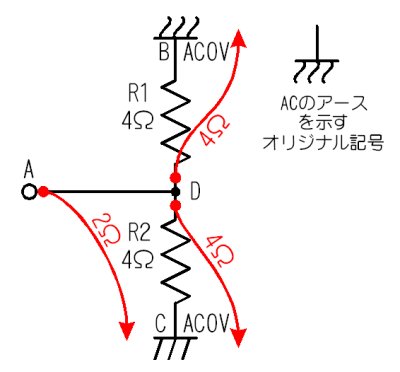
夞楬恾偐傜僀儞僺乕僟儞僗傪媮傔傞
丂偙傟傑偱峫偊偨偙偲傪傑偲傔偰丄夞楬恾傪彂偒捈偡偲忋恾偺傛偆偵側傝傑偡丅
丂俢揰偐傜壓傪尒傞偲俼俀偺係兌偑偁傝丄俢揰偐傜忋傪尒傞偲俼侾偺係兌偑偁傝傑偡丅俙揰偐傜尒傟偽俀偮偺係兌偼暲楍偵側傞偺偱丄倅倝亖係兌乛乛係兌亖俀兌偲媮傔傜傟傑偡丅
弌椡僀儞僺乕僟儞僗偲偼
丂偁傞夞楬偺弌椡偺岎棳掞峈偑偳偺偔傜偄偁傞偐丠偲偄偆偙偲偱偡丅偮傑傝丄壓偺恾偱丄愒怓偱帵偡倅俷偺抣偑壗兌偐丄偲偆偙偲偱偡丅
丂擖椡僀儞僺乕僟儞僗偲堘偆偺偼丄怣崋乮岎棳乯弌椡傪弌偟偱偄傞抂巕偺僀儞僺乕僟儞僗偩偲偄偆偲偙傠偱偡丅
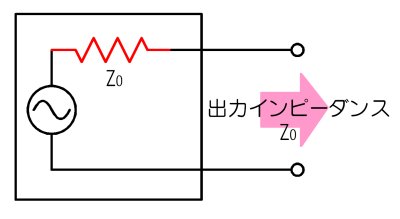
弌椡僀儞僺乕僟儞僗偲偼
丂應掕偺巇曽偼偪傚偭偲柺搢丅師偺俁僗僥僢僾偱峴偄傑偡丅
- 弌椡抂巕偵揹棳傪棳偝偢丄弌椡怣崋揹埑倴倧乫傪應掕偟傑偡
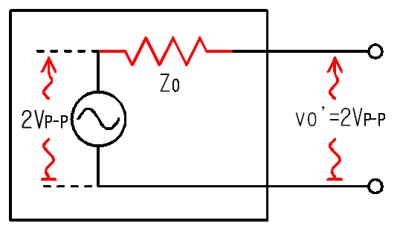
奐曻弌椡揹埑vo'傪應掕偡傞
應掕偟偨倴倧乫偑俀倁俹亅俹偱偁傟偽丄敔偺拞偵偁傞怣崋尮偺揹埑偼嫲傜偔俀倁俹亅俹偱偟傚偆丅
- 弌椡抂巕傪岎棳揑偵抁棈乮僔儑乕僩乯偟偰丄弌椡揹棳俬o傪應掕偟傑偡
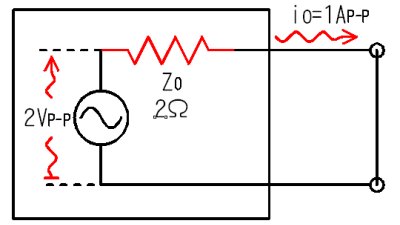
抁棈弌椡揹棳倝倧傪應掕偡傞丅
偙偙偱偼丄侾俙俹亅俹偺揹棳偑棳傟傑偟偨丅
捠忢偼岎棳偺傒傪抁棈偡傞偨傔偵丄僐儞僨儞僒偱抁棈偟偨偲峫偊傑偡丅
- 倅倧亖倴倧乫亐俬倧偲寁嶼偟偰弌椡僀儞僺乕僟儞僗傪媮傔傑偡
偙偺椺偱偼乧
倅o亖俀倁俹亅俹亐侾俙俹亅俹亖俀兌
偲側傝傑偡丅
夞楬恾偐傜弌椡僀儞僺乕僟儞僗傪媮傔傞
丂幚偼丄愭傎偳偺夞楬丄僼僞傪奐偗偰傒傞偲丄師恾偺傛偆側攝慄偵側偭偰偄傑偟偨丅偝偰丄夞楬偐傜弌椡僀儞僺乕僟儞僗傪媮傔偰傒傑偟傚偆丅
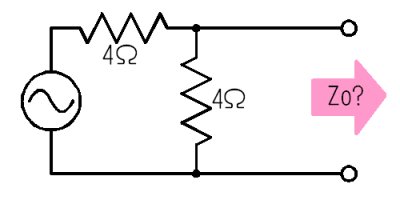
夞楬偐傜僀儞僺乕僟儞僗傪媮傔傞
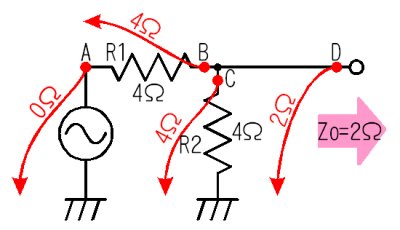
奺揰偐傜傒偨僀儞僺乕僟儞僗
夞楬偐傜僀儞僺乕僟儞僗傪媮傔傞庤弴偼師偺捠傝偱偡丅
- 俙揰偐傜怣崋尮傪尒傞偲侽兌偱偡丅乮怣崋尮偺弌椡僀儞僺乕僟儞僗偼侽兌偩偐傜偱偡乯
- 俛揰偐傜怣崋尮偺曽岦傪尒傞偲丄怣崋尮偺侽兌偲俼侾偺係兌偑捈楍偵側偭偰偄傞偺偱丄係兌偵尒偊傑偡
- 俠揰偐傜傾乕僗傪尒傞偲丄俼俀偑偁傞偺偱係兌偵尒偊傑偡丅
- 弌椡抂巕偺俢揰偐傜怣崋尮懁傪尒傞偲丄俛揰偺係兌偲俠揰偺係兌偑暲楍偵尒偊傞偺偱丄弌椡僀儞僺乕僟儞僗偼丄係兌乛乛係兌亖俀兌偲側傝傑偡丅
僩儔儞僕僗僞夞楬偺僀儞僺乕僟儞僗
儀乕僗偺僀儞僺乕僟儞僗
俬俤俤偑侾倣俙棳傟丄倰倕偑俀俇兌偲側偭偰偄傞丄壓恾偺僩儔儞僕僗僞偺儀乕僗偺擖椡僀儞僺乕僟儞僗傪峫偊偰傒傑偟傚偆丅
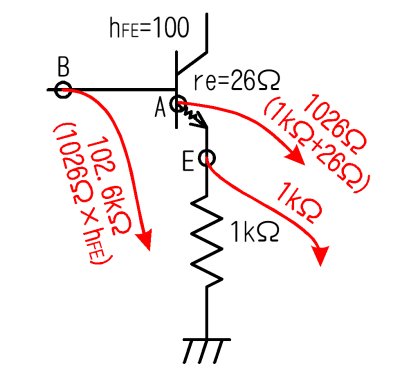
儀乕僗偺僀儞僺乕僟儞僗
- 俤揰偐傜傾乕僗曽岦傪尒傞偲丄俼俤偑偁傞偺偱丄僀儞僺乕僟儞僗偼侾倠兌偱偁傞丅
- 俙揰乮僩儔儞僕僗僞偺儀乕僗偺棤懁乯偐傜尒傞偲丄倰倕偲俼俤偑捈楍偵尒偊傞偺偱丄侾倠兌亄俀俇兌偱侾侽俀俇兌偵尒偊傞丅
- 僩儔儞僕僗僞偼揹棳傪倛俥俤攞偵憹暆偡傞偺偱丄俛揰乮儀乕僗乯偐傜傒傞偲丄僀儞僺乕僟儞僗偼俙揰偺倛俥俤攞偵尒偊傞丅
- 廬偭偰丄偙偺夞楬偺儀乕僗偺擖椡僀儞僺乕僟儞僗偼倛俥俤亊乮倰倕亄俼俤乯偱寁嶼偱偒丄侾侽侽亊乮俀俇亄侾侽侽侽乯亖侾侽俀丏俇倠兌偲側傞丅
僄儈僢僞偺僀儞僺乕僟儞僗
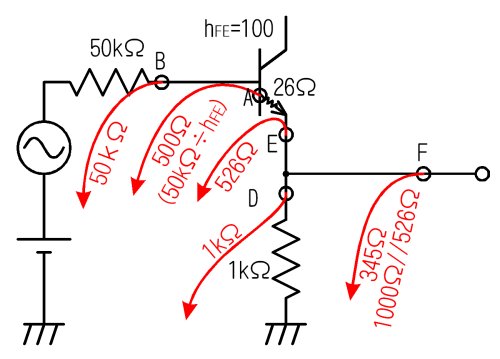
俬俤俤偑侾倣俙棳傟丄倰倕偑俀俇兌偲側偭偰偄傞丄壓恾偺僩儔儞僕僗僞偺僄儈僢僞偺弌椡僀儞僺乕僟儞僗傪峫偊偰傒傑偟傚偆丅
儀乕僗偺僀儞僺乕僟儞僗
- 俛揰偐傜擖椡懁傪尒傞偲丄俆侽倠兌偑尒偊傞
- 俙揰乮僩儔儞僕僗僞偺儀乕僗偺棤懁乯偐傜偼丄俛揰偺俆侽倠兌偑乮揹棳偑倛俥俤攞偵憹偊傞偨傔乯倛俥俤暘偺侾偵尒偊傞偺偱丄俆侽侽兌偵尒偊傞
- 俤揰偐傜偼丄俙揰偺俆侽侽兌偲倰倕偺俀俇兌偑捈楍偵尒偊傞偺偱丄俆俀俇兌偵尒偊傞
- 媡偵俢揰偱偼丄俼俤偑偁傞偨傔丄侾倠兌偑尒偊傞
- 弌椡抂巕俥揰偱偼丄俤揰偺俆俀俇兌偲俢揰偺侾倠兌偑僷儔偵尒偊傞偺偱丄俆俀俇乛乛侾侽侽侽亖俁係俆兌偵尒偊傞
僐儗僋僞偺僀儞僺乕僟儞僗乽岺帠拞乿
丂僩儔儞僕僗僞偺僐儗僋僞偺僀儞僺乕僟儞僗偑亣偱偁傞偙偲傪愢柧偟傑偡丅
俀抜憹暆婍乽岺帠拞乿
丂僄儈僢僞愙抧偲僄儈僢僞僼僅儘傾傪慻傒崌傢偣偨俀抜憹暆婍偺愝寁曽朄傪専摙偟傑偡丅
嵎摦憹暆婍乽岺帠拞乿
丂僩儔儞僕僗僞偺寚揰傪懪偪徚偟丄敳孮偺埨掕惈傪傕偮嶌摦憹暆婍偺摦嶌尨棟偲愝寁曽傪愢柧偟傑偡丅
僇儗儞僩儈儔乕乽岺帠拞乿
丂嶌摦憹暆婍傗偁偲偱愢柧偡傞擻摦晧壸偵巊梡偡傞婎杮夞楬偱偁傞僇儗儞僩儈儔乕偺摦嶌尨棟偲愝寁曽朄傪愢柧偟傑偡丅
愝寁偲帋嶌乮儈僯僷儚乕傾儞僾乯乽岺帠拞乿
丂偙傟傑偱偺抦幆傪妶偐偟偰丄億乕僞僽儖僆乕僨傿僆傪愙懕偟偰僗僺乕僇乕傪柭傜偡偙偲偺偱偒傞乽姰慡僨傿僗僋儕乕僩丒儈僯僷儚乕傾儞僾乿傪帺椡偱愝寁丒帋嶌偟傑偡丅偙偙傑偱棃傟偽丄偐側傝偺愝寁椡偑晅偄偰偄傑偡丅
擻摦晧壸乽岺帠拞乿
丂崅偄憹暆棪傪摼傞偙偲偺偱偒傞僥僋僯僢僋傪徯夘偟傑偡丅

















































